Rep:Mod:chem2010c2

Module 3 - Physical Computing Lab

Olivia Highland

Introduction

In this module the different transition states in the Cope rearrangement and the Diels-Alder reaction on their respective potential energy surfaces. In this module the MO methods are used in order to solve the Schrodinger Equation and the transition states are found by traversing the Potential Energy Surface.

At all points along the reaction curve (although this can be visualised in 3D which would make it more of a potential energy surface) there are 3N-6 vibrations for the molecule. At the points for the reactant and the product the frequencies are all at a minimum, with none at a greater intensity than any of the others and they are all perpendicular to each other. However, at the transition state one of the frequencies is amplified, this frequency corresponds to the frequency which represents the bonds changing from their position in the reactant to their position in the product. This is why, when the transition state is found there should only be one imaginary frequency. On the curve between the reactant and the transition state the vibrations are constantly morphing into the vibrations found at either end of the curve.

The Cope Rearrangement

The molecule under consideration in this section is 1,5- hexadiene, using this molecule we will use find the low energy minima and transition states. The [3,3]-sigmatropic shift proceeds via a concerted mechanism which have either a chair or boat transition phase. In this exercise it will be seen which transition state is more likely to take place.

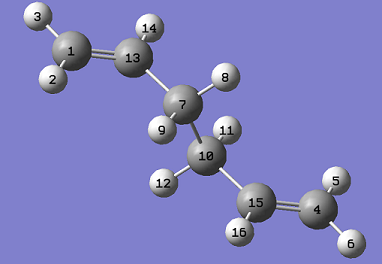
The lowest energy conformation of the 1,5-hexadiene was found, initially by creating the conformation with the carbon atoms 2-4 in an anti peri planar conformation. The next conformation to be found was when the atoms 2-4 were in the Gauche conformation, then the Ci conformer is found by having all the carbon atoms in an anti peri planar conformation to each other. It was found that the Gauche conformation has the lowest energy, rather than the expected lowest energy for the anti peri planar conformation, where there are the lowest amounts of interactions between the different groups as none of them are eclipsed with each other. However, in this case there may be some favourable Hydrogen bonding interactions between the Hydrogen groups coming off of the carbons. In the anti per planar arrangement the distances between the hydrogens is approximately 2.5 Angstroms, whereas in the gauche conformation the distance between the Hydrogen atoms is 2.43 Angstroms, with the attraction between two Hydrogen atoms being at a maximum as the internuclear distance approaches 2.4 Angstoms, and becomes repulsive once that distance becomes closer than 2.1 Angstroms. All of the different molecules are at a minimum because the RMS gradient is less than 0.00001 a.u.

The report summary for different conformers:

	Anti periplanar	Gauche	Ci
File Type	.fch	.fch	.fch
Calculation Type	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	3-21G	3-21G	3-21G
Total Energy	-231.6926 a.u.	-231.6927 a.u.	-231.6925 a.u.
RMS Gradient Norm	0.00001211 a.u.	0.00002439 a.u.	0.00001891 a.u.
Dipole Moment	0.2022 Debye	0.3408 Debye	0.0000 Debye
Image
Point Group	C2	C1	Ci
Energy kcal/mol	0.04	0.00	0.08

When the two different optimisations are compared for the 1,5 hexadiene, the first optimisation is done using the HF/3-21G level of theory and the second one is done using the B3LYP/6-31G* level - When this was reoptimised then the new energy is -234.56 a.u. - this is a more detailed basis set; now, minuscule changes can be seen, these cannot be seen simply when the molecules are viewed side by side. However, when the different bond lengths are compared and the different dihedral angles are measured, then it can be seen clearly that the molecule has been optimised to a new degree of accuracy:

Segment under observation	Optimisation 1	Optimisation 2	Literature
Dihedral angle 8,7,10,11 (Degrees)	-62.83	-64.15	-
Dihedral Angle 1,13,7,10 (Degrees)	114.67	118.67	116.0
Dihedral Angle 14,13,7,8 (Degrees)	55.82	59.95	-
Dihedral Angle 14,13,7,9 (Degrees)	174.27	177.07	178.3
Bond Length 7-10 (Angstroms)	1.552	1.555	1.536
Bond Length 1-13 (Angstroms)	1.316	1.338	1.341
Bond Length 13-7 (Angstroms)	1.509	1.507	1.508

The final energies given in the output file represent the energy of the molecule on the bare potential energy surface. To be able to compare these energies with experimentally measured quantities, they need to include some additional terms, which requires a frequency calculation to be carried out. The frequency calculation can also be used to characterize the critical point, i.e. to confirm that it is a minimum in this case: that all vibrational frequencies are real and positive.

The final energies that are taken from the summary of the information in the output file for each of the different optimised conformations only represents the energy of the molecule on the potential energy surface, and is a way of analysing the minimum energy conformations of different molecules computed within Gaussian. However, in order to compare these energies with those extracted from different experimental techniques then a frequency analysis needs to be taken. This frequency analysis will take the second differential of the system and prove that the conformation is at a minimum and not at a transition point (on a graph the point at which there is a zero gradient can be a minimum, a maximum or a turning point, the second differential will establish which point the molecule is really at on the potential energy curve. If, when the different vibrations are analysed and there are 2 minimum values then the molecule is at a transition state. If there is only one negative frequency then the molecule is at its minimum energy conformation. When the frequency is taken for this simulation then it can be seen clearly that there are no imaginary frequencies as none of the vibrations are negative, the smallest vibration is at 71.85 cm-1, providing the following spectrum:

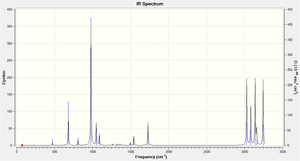
The peak at 680.09 cm-1 corresponds to a C-H bend, at 1016.36cm-1 this is a C-C bond stretch, at 1728.20cm-1 a C=C bond stretch and then at 3000+ frequencies these vibrations correspond to the CH stretches throughout the molecule.

The different vibrations produced from the molecule:

Images
Vibration / cm-1	471.03	680.09	1016.36	1728.20	3139.28
Type	'rocking' motion	C-H bond stretching	C-C bond stretching	C=C bond stretching	C-H bond stretching

The report summary for the second optimisation of the 1,5 hexadiene:

Type	Energy (a.u.)
Sum of electronic +zero point energies (E=Eelec +ZPE)	-234.42
Sum of electronic + thermal energies (E = E + Evib + Erot + Etrans)	-234.41
Sum of electronic + thermal enthalpies (H = E + RT)	-234.41
Sum of electronic + thermal free energies (G = H - TS)	-234.45

Extra for Chair

The frequency calculated after the first optimisation of the transition state is approximately 818cm-1, it can be seen that this is the transition state because there is only one imaginary frequency, so this frequency is the one corresponding to the Cope Rearrangement. Now the second optimisation takes place, where the coordinates need to be frozen. This freezes the atoms where the bonds are either to be formed or to be broken and then the bond length that needs to be placed there can be set (in this case the bond length is set at 2.2 Angstroms). This aids in optimising the structure further. When this is reopened the differences between the new optimised structure and the initially optimised structure is that after the first optimisation the 'newly formed' bonds were 2.02 Angstoms in length and now they are set to 2.2 Angstroms. These bonds will now be the focus of the optimisation, where using the Redundant Coordinate Editor as was used in the previous optimisation step, instead of freezing the coordinates of the terminal carbons, the bonds will be differentiated along, which will modify them to their 'true' length. This changes the bond length back to 2.02 Angstroms, the same length that it was after the first optimisation.The vibration is -818.03cm-1 after these optimisations, which is only a small change from the initial optimised imaginary frequency.

Extra for Boat

For the boat transition structure a different method will be used optimise the transition state. In this method the QST2 method is used. In this method the reactant and the product are specified in adjacent windows; the reactant and product are then numbered correctly so that the programme can understand where the bonds will be broken in the reactant and formed in the product, these numbers need to be done accurately for both the carbons and the hydrogens. The programme can now interpolate between the reactant and the product and try to find the minimum energy transition state whose structure is found somewhere between the reactants and the products.

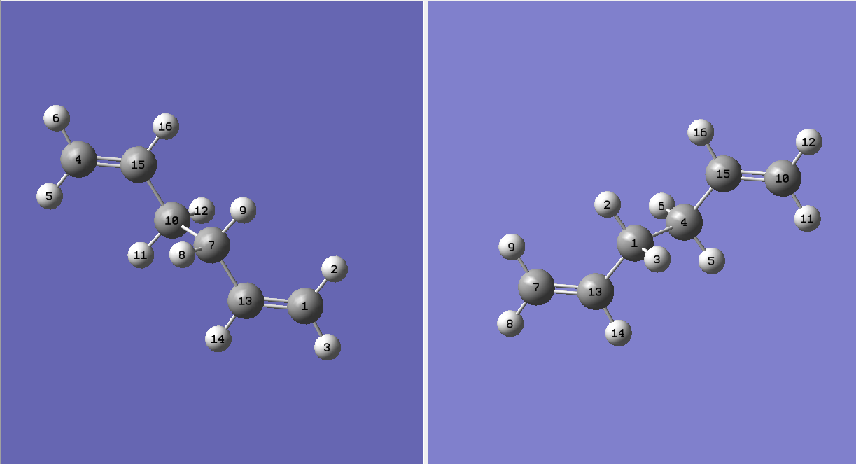
When the first QST2 calculation is attempted then it can be seen that the optimisation does not produce the correct structure for the transition state, in effect the job has failed. With its current geometry the programme cannot predict the correct transition state structure; it was predicted that the transition state structure would look a 'bit like the chair transition sructure but more dissociated.' , instead when my own optimisation was run it created a different higher energy transition state which did indeed seem to have a slight chair structure, however the atoms were not dissociated; instead the bonds which would have created a boat structure hexadiene crossed over in the middle of the two fragments, as can be seen below:

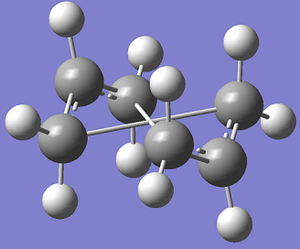
In order to correct this failure within Gaussview the structure needs to resemble the boat transition structure more closely, thus, for both the reactant and the product the central 4 carbon atoms were altered in the following way: C13-C7-C10-C15 (for the reactant) had the dihedral angle changed to be 0 degrees and then the internal angles for C13-C7-C10 and C7-C10-C15 were altered to be 100 degrees. The same alterations were made for the corresponding atoms in the product molecule. The QST2 calculation was then run again, this time the simulation ran correctly, producing the transition state, this was verified as there is only one imaginary frequency at -840.15cm-1.

It should be noted here that as a further experiment I checked whether the same results would be produced by proceeding to the boat transition state using the same freeze coordinates method as had been used in the chair section of the simulation. The different method produced identical results to those found using the QST2 method. This shows that later on in the Diels Alder section of the experiment, in order to achieve the transition state it is completely inconsequential regarding which method is to be used.

IRC

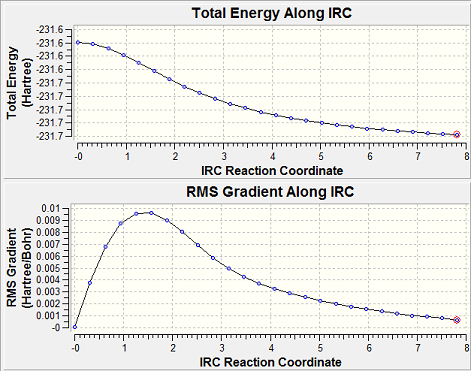
When the boat and chair transition structures are examined it is almost impossible, from observation alone to predict from the transition state which initial conformation of 1,5- hexadiene was used. However, using Gaussview it is possible to find the minimum energy path from the transition state across the potential energy surface back to the reactant. This method is called the Intrinsic Reaction Coordinate method (IRC); it works by taking small steps until it finds the local point where the gradient of the potential energy surface of the molecule is at its steepest, here it has found its minimum. As our reaction coordinate is symmetrical we will only calculate the forwards direction as computing it in both directions for a symmetrical molecule will only double the number of points plotted rather than alter the results in any sort of way. The number of points that are computed along the IRC is changed here from the standard 6 points to a more detailed view of 50 points. When the checkpoint files were opened it was clear that neither structure had reached its minimum geometry, the chair transition state had reached only 26 steps and the boat had reached 19 steps. There were now 3 different options which could be taken in order to get the molecule to the minimum geometry, the last point on the IRC could be taken and a minimisation calculation could be taken on this point, the IRC could be restarted and a larger number of points would need to be attempted until a minimum was reached (the maximum number of points that the programme can run is 400 points), or the IRC could be rerun specifying that the force constants should now be calculated at every step rather than only the once as they had been done previously. The third option was taken on both molecules as the molecule is not too large and the computational time required, was not too long (a few minutes). The IRC for the chair was now complete after 43 steps:

	IRC 1	IRC 2
Molecule Image
Differences	In this optimisation the two fragments have only separated a small bit, the fragments have not twisted over each other either.	In this optimisation the two fragments have increased their separation and the angle between them is much larger, in addition the two fragmentshave twisted over each other into a lower energy conformation.
Energy (a.u.)	-231.689	-231.691
IRC Charts

The chair conformation that was produced after more iterations is lower in energy than the one that was produced after only 26, making this the most stable conformation. When the IRC charts are looked at, after the first set of iterations there is the biggest change in gradient, with the change in gradient, with the change in gradient ranging from 0 to 0.01 in the first IRC calculation, whereas after the second iteration the gradient change is only from 0 to 0.00065; so the largest change in the structure takes place, the second set of iterations does not have as great a change in energy or a change in gradient, instead the programme is simply refining the conformation that it has found. When the final IRC point is symmetrized then it can be seen that it has C2 symmetry with -231.69167 au energy, this makes the starting conformation gauche2.

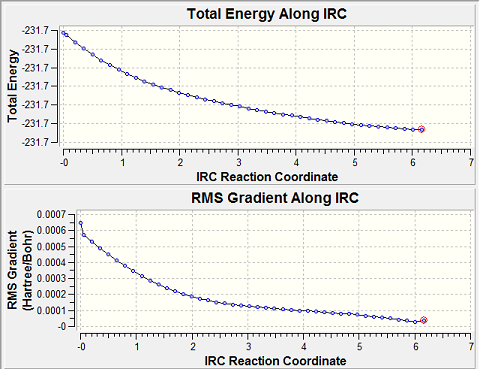
In addition the IRC of the boat transition state was also considered:

	IRC 1	IRC 2	IRC 3
Molecule Image
Differences	After 19 iterations the separation between the two fragments is small and has clearly not come to a minimum	After 51 iterations (which is unusual as the number of iterations was limited to 50 and it was purely in the forwards direction) the separation is greater, however there is no twisting in the structure and the calculation has not reached a minimum. So in this case more iterations are required, this time the full limit of 400 was set and the simulation was done again.	After 90 iterations the minimum path has been found and the geometry of the molecule has twisted.
Energy (a.u.)	-231.671	-231.683	-231.693
IRC Charts

It can be seen from the IRC charts that after the first iteration the steepest part of the gradient is traversed and also there is the largest change in the energy. For the second iteration the change in the energy and gradient levels off as it did in the IRC for the chair, after this for the third iteration a more stable conformer was found as the change in the gradient reaches a new low and the lowering in the energy is even greater. When the conformer is symmetrized the point group is found to be C1, with an energy of -231.69266 the minimum energy gauche3 configuration was used.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair Transition State	-231.619322	-231.466325	-231.459883	-234.554988	-234.414477	-234.408921
Boat Transition State	-231.602802	-231.450143	-231.444987	-234.554309	-234.402321	-234.395899
Reactant (anti2)	-231.692602	-231.539511	-231.532461	-234.559670	-234.468213	-234.461768

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.92	45.54	33.72	33.16	33.5 ± 0.5
ΔE (Boat)	56.08	54.89	41.35	41.33	44.7 ± 2.0

The conversion rate between the Hartree and kcal/mol is 1 Hartree: 630 kcal/mol

It can be seen clearly that the HF/3-21G basis set produces the greatest difference between the activation energies in the simulation and those gained from experimentation. However, the values gained from the B3LYP/6-31G* method are much closer to the experimental values, proving that the larger a basis set used the more accurate the results gained from the simulations.

Diels Alder

In this section, the same techniques that were utilised during the Cope Rearrangement Tutorial are to be used in looking at the Diels-Alder reaction. Similarly to the Cope Rearrangement the Diels-Alder reaction is a concerted pericyclic reaction, in this section the reaction will be between butadiene and ethylene, this is a [4 + 2] cycloaddition. In the Diels-Alder cycloaddition the pi orbitals of the dienophile create new sigma bonds with the pi orbitals of the diene. The HOMO and LUMO molecular orbitals play an important part in determining whether the reaction is allowed or forbidden. The reaction is allowed if the HOMO of a reactant can interact with the LUMO of the other reactant. The reaction is forbidden when there is not enough overlap between the HOMO and LUMO orbitals - which normally occurs if the orbitals have a greater difference in symmetry. In this reaction however, there are other secondary orbitals which can stabilise one regiochemistry over the other (stabilising the endo form rather than the expected exo form.). In this section instead of the B3LYP/6-31G* or the HF/3-21G basis set, the semi-empirical molecular orbital AM1 method is used.

The orbitals that overlap for the above reaction are the π/ π* orbitals of the ethylene and these orbitals interact with the HOMO/LUMO orbitals of the butadiene molecule. In this reaction the orbitals that we are expecting to overlap are the HOMO-LUMO pairs in order to make the reaction allowed as these HOMO-LUMO pairs have the same symmetry so in theory there should be good overlap between the orbitals.

	HOMO butadiene	LUMO butadiene	HOMO ethylene	LUMO ethylene
Molecule Image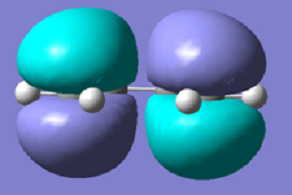
Energies (angstroms)	-0.343	0.017	-0.387	0.052

From the above images it is clear that the LUMO of the butadiene is symmetric with respect to the reflection plane, and the HOMO is antisymmetric with respect to the reflection plane. In the same way the HOMO of the ethylene is symmetric and the LUMO of the ethylene is antisymmetric; as the HOMO-LUMO interactions are all symmetric then the interactions would be favourable and are allowed.

Using the freeze coordinates method used to calculate the transition state for the chair conformation of the cope rearrangement; the transition state for the Diels-Alder reaction between cis-butadiene and ethylene has been simulated. The interfragmental distance was guessed to be approximately 2.1 Angstroms, value taken from the Cope rearrangement tutorial. It is conformed that the transition state is reached, with a single imaginary frequency of -956.82cm-1, and an energy of 0.112 a.u.:

In this vibration it can be seen that the newly formed 'bonds' vibrate synchronously, this is further proof that the reaction is concerted. However, the first positive vibration does not have simultaneous stretches (147.80cm-1), the stretches are antisymmetric so they are asynchronous:

	HOMO Diels Alder	LUMO Diels Alder
Molecule Image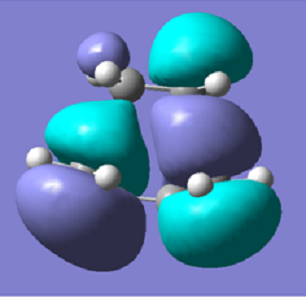
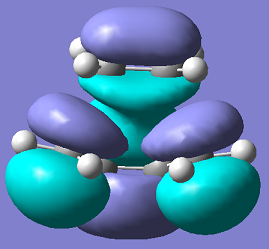Energies (angstroms)	-0.323	0.023

It is clear from the MO diagrams that the HOMO for the transition state comes from the HOMO of the butadiene and the LUMO of the ethylene mixing together, as they have the same symmetry, and produces an antisymmetric molecule about the reflection plane. The LUMO of the transition state comes from the mixing of the LUMO of the butadiene and the HOMO of the ethylene, they mix as the orbitals have the same symmetry and they produce a symmetrical molecule about the reflection plane.

The literature values for sp3-sp3 C-C bond length is 1.54 Angstroms, the value for the sp2-sp2 C-C bonds length is 1.33 Angstroms. In this simulation the values that were found for the sp2 C-C bond length is 1.38 Angstroms. This is only 0.05 Angstroms away from the literature value, the simulation is relatively accurate. The sp2 sp2 bond angle is 120 degrees, which agrees exactly with the value expected from the literature. The Van der Waals radius for the carbon atom is 1.7 Angstroms, the bond length of the newly formed bonds between the termini of the fragments is 2.12 Angstroms, thus the electron density surrounding each of the carbon atoms on the termini will overlap, leaving enough electron density for a bond to be formed, this is in accordance with the rules for whether bonds will be formed between the two fragments, as is stated above.

1,3-cyclohexadiene reaction with Maleic Anhydride

In this section of the module, the 1,3-cyclohexadiene reacts with Maleic Anhyride to mainly give the endo product, due to the endo rule as has been explained in the above introduction to the Diels Alder section. In this section the following reaction scheme took place:

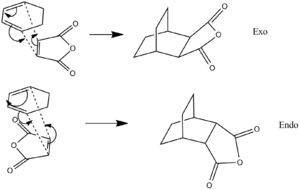
Again the Freeze coordinates method was used on the 1,3-cyclohexadiene and Maleic Anhydride fragments to produce the following exo or endo transition states, which had following vibrations:

	Exo	Endo
Molecule Image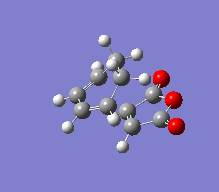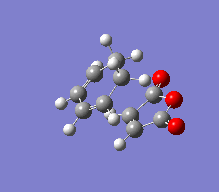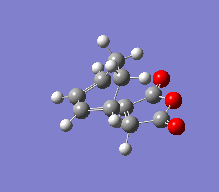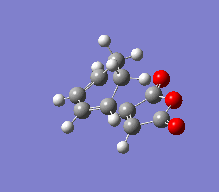
Frequencies (cm-1)	-812.28	-806.365
Energies (a.u.)	-0.0504	-0.0515

For both the transition states it is apparent that the creation of the bonds, following the theory that the mechanism is concerted. As predicted due to the endo rule (that secondary orbitals participate in stabilising the new sigma bond that has been created in the Diels-Alder reaction), the Endo transition state has a more stable energy than the exo state by 0.0011 a.u. The frequency is less engative for the endo state, showing that the bond created in the endo reaction is more stable.

The newly formed sigma bond lengths for the endo transition state is 2.16 Angstroms, for the exo transition state is 2.17 Angstroms. Similarly to the previous section the sp2 C-C bond lengths are 1.39 Angstroms for both transition states. The angles between the top fragment and the bottom fragment in the exo is 99.9 degrees, whereas for the endo product this angle is 96.7 degrees.

	Exo HOMO	Endo HOMO
MO images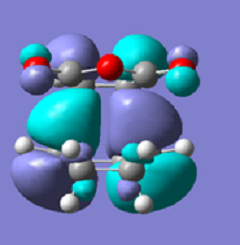
Energies (a.u.)	-0.342	-0.345

It can be seem from these Molecular Orbital diagrams that they are both antisymmetric about the reflection plane, probably due to the overlap of the HOMO of the 1,3-hexadiene and the LUMO of the Maleic Anhydride. From the energies of the MO energy levels it can be seen that the energy of the Endo HOMO is lower than the energy of the Exo HOMO, again showing stabilisation from secondary orbitals. When considering the -(C=O)-O-(C=O)- fragments in both the Endo and Exo transition state MO's the Exo product has no electron density across these bonds, making it more unstable than the Endo transition state where there is some electron density. Thus the secondary orbital overlap effect plays a large part in making the Endo form more stable - even at the transition state point than the Exo.

In the simulation only a single molecule is considered. However, when the reaction is undertaken in the Laboratory, it is not only one molecule which is in the solution, there are millions. All these different molecules will have an effect on each other, with their forces affecting each others geometries and their different bond lengths and angles.