Rep:Mod:chem2010c

Module 3 - Physical Computing Lab

Olivia Highland

Introduction

In this module the different transition states in the Cope rearrangement and the Diels-Alder reaction on their respective potential energy surfaces. In this module the MO methods are used in order to solve the Schrodinger Equation and the transition states are found by traversing the Potential Energy Surface. ADD SOME MORE TO THIS INTRO.

The Cope Rearrangement

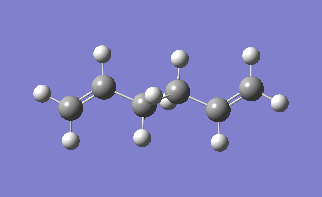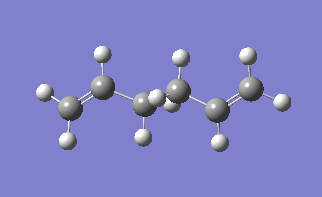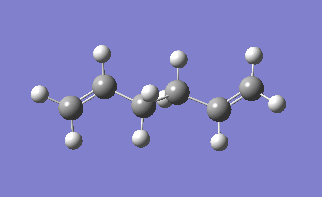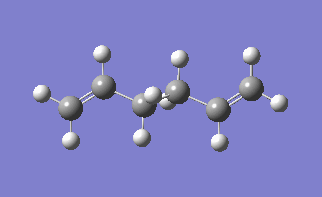
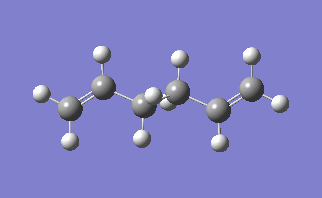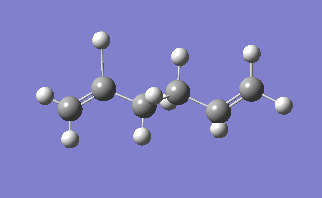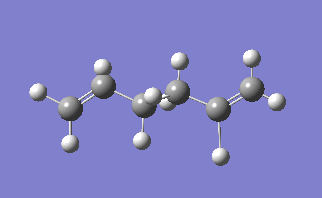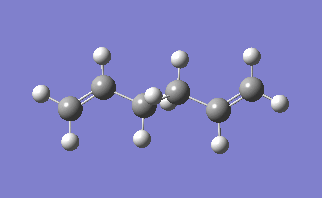
The molecule under consideration in this section is 1,5- hexadiene, using this molecule we will use find the low energy minima and transition states. The [3,3]-sigmatropic shift proceeds via a concerted mechanism which have either a chair or boat transition phase. In this exercise it will be seen which transition state is more likely to take place.

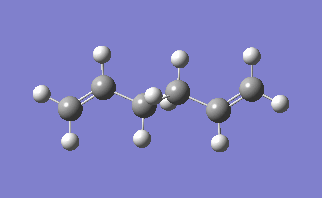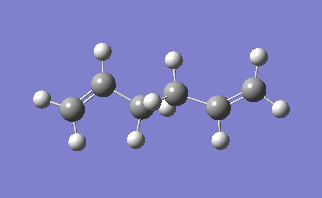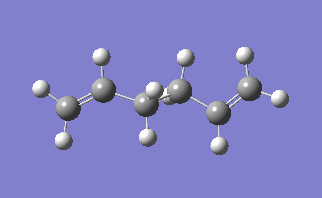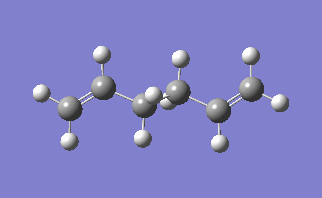
The lowest energy conformation of the 1,5-hexadiene was found, initially by creating the conformation with the carbon atoms 2-4 in an anti peri planar conformation. The next conformation to be found was when the atoms 2-4 were in the Gauche conformation, then the Ci conformer is found by having all the carbon atoms in an anti peri planar conformation to each other. It was found that the Gauche conformation has the lowest energy, rather than the expected lowest energy for the anti peri planar conformation, where there are the lowest amounts of interactions between the different groups as none of them are eclipsed with each other. However, in this case there may be some favourable Hydrogen bonding interactions between the Hydrogen groups coming off of the carbons. In the anti per planar arrangement the distances between the hydrogens is approximately 2.5 Angstroms, whereas in the gauche conformation the distance between the Hydrogen atoms is 2.43 Angstroms, with the attraction between two Hydrogen atoms beign at a maximum as the internuclear distance approaches 2.4 Angstoms, and becomes repulsive once that distance becomes closer than 2.1 Angstroms. All of the different molecules are at a minimum because the RMS gradient is less than 0.00001 a.u.

The report summary for different conformers:

	Anti periplanar	Gauche	Ci
File Type	.fch	.fch	.fch
Calculation Type	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	3-21G	3-21G	3-21G
Total Energy	-231.6926 a.u.	-231.6915 a.u.	-231.6925 a.u.
RMS Gradient Norm	0.00001211 a.u.	0.00001866 a.u.	0.00001891 a.u.
Dipole Moment	0.2022 Debye	0.1281 Debye	0.0000 Debye
Image
Point Group	C2	C2	Ci
Energy kcal/mol	0.04	0.71	0.08

The energy found for the molecule with Ci symmetry is identical to the energy provided in the table in the notes. Once it was certain that the structures were identical then the structure was reoptimised at the B3LYP/6-31G* level. When this was reoptimised then the new energy is -234.56 a.u. the difference in the energies is -287 a.u., when the two different structures are compared then not much of a difference can be noticed between the two structures overall, however by using a different basis set then a more accurate optimisation can be achieved.

The final energies given in the output file represent the energy of the molecule on the bare potential energy surface. To be able to compare these energies with experimentally measured quantities, they need to include some additional terms, which requires a frequency calculation to be carried out. The frequency calculation can also be used to characterize the critical point, i.e. to confirm that it is a minimum in this case: that all vibrational frequencies are real and positive.

The final energies that are taken from the summary of the information in the output file for each of the different optimised conformations only represents the energy of the molecule on the potential energy surface, and is a way of analysing the minimum energy conformations of different molecules computed within Gaussian. However, in order to compare these energies with those extracted from different experimental techniques then a frequency analysis needs to be taken. This frequency analysis will take the second differential of the system and prove that the conformation is at a minimum and not at a transition point (on a graph the point at which there is a zero gradient can be a minimum, a maximum or a turning point, the second differential will establish which point the molecule is really at on the potential energy curve. If, when the different vibrations are analysed and there are 2 minimum values then the molecule is at a transition state. If there is only one negative frequency then the molecule is at its minimum energy conformation. When the frequency is taken for this simulation then it can be seen clearly that there are no imaginary frequencies as none of the vibrations are negative, the smallest vibration is at 71.85 cm-1, providing the following spectrum:

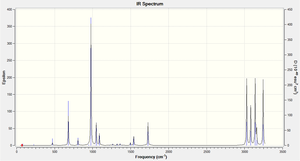
The peak at 680.09 cm-1 corresponds to a C-H bend, at 1016.36cm-1 this is a C-C bond stretch, at 1728.20cm-1 a C=C bond stretch and then at 3000+ frequencies these vibrations correspond to the CH stretches throughout the molecule.

The different vibrations produced from the molecule:

Images
Vibration / cm-1	471.03	680.09	1016.36	1728.20	3139.28
Type	'rocking' motion	C-H bond stretching	C-C bond stretching	C=C bond stretching	C-H bond stretching

The report summary for the second optimisation of the 1,5 hexadiene:

Type	Energy (a.u.)
Sum of electronic +zero point energies (E=Eelec +ZPE)	-234.42
Sum of electronic + thermal energies (E = E + Evib + Erot + Etrans)	-234.41
Sum of electronic + thermal enthalpies (H = E + RT)	-234.41
Sum of electronic + thermal free energies (G = H - TS)	-234.45

Optimising the 'chair' and 'boat' conformations

In this section the transition structures of the chair and boat conformers will be examined. In order to achieve this then the force constants need to be computed, then use the redundant coordinate editor and by using the QST2. The activation energies for the cope rearrangement via both the boat transition step and then by the chair transition state will be calculated in order to see which will be the most likely transition step for the reaction to take place. Initially a fragment of CH2CHCH2 is created and then this fragment is optimised, using the HF-3-21G method. This fragment is the basis for calculating the transition steps. Two different methods will be used in this section to calculate the transition steps; a different method for both the chair and the boat conformation.

Chair

Initially the optimised CH2CHCH2 fragment is copied twice and placed above each other, the fragments are then orientated so that they will proceed to a chair transition state. The two optimisations for the structures are initially using a gaussian minimisation with TS (Berny), the programme is asked to compute the force constants one and with the option of Opt=NoEigen which stops the calculation from crashing should more than one imaginary frequency be calculated during the optimisation. When this optimisation is complete then an imaginary frequency should be calculated and found at 818 cm-1:

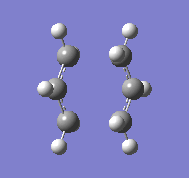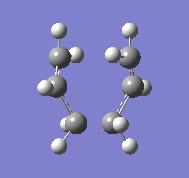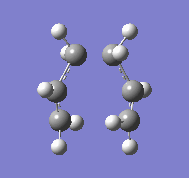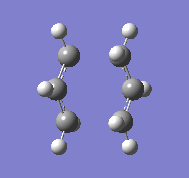
In the vibration it can be seen that the bonds which appear to be vibrating do not exist, these are the bonds that are meant to occur between the terminals of each of the fragments.

For the second optimisation the Redundant Coordinate editor is used to Freeze the coordinates of the terminal atoms in the fragements. Then the optimisation proceeds as before, but the bonds between the fragments are now set to 2.2 Angstroms. Once the bonds have bond breaking/forming distances have been optimised again their lengths decrease from both being 2.02 Angstroms after the first optimisation to being 2.2 and 2.14 Angstroms. The energy for the chair conformation is -231.62 a.u.

The chair optimised transition step:

Boat

In this section of the module the boat transition state is going to be optimised, this will be done using the QST2 method instead of the optimisation method used for the Chair conformation. In this method the reactant and product are specified, after which the programme goes through the different potential energies between the molecules and tries to find the minimum transition state for the two molecules. When the molecules were first put into separate windows so that both the product and the reactant could be worked on at the same time they both needed to be numbered correctly so that the optimisations would proceed correctly:

The numbered chains:

The numbering needs to be done correctly otherwise Gaussview will not know which bonds to break and which new bonds it needs to form in the concerted reaction. Here the bond between atom 7 and 10 has been broken and the bond between 4 and 1 has been created. When the TS(QST2) method is used the job fails. Instead of the suggested dissociation of the atoms which should accompany this failure, in this case I found a different transition state:

Instead of being a boat transition state the transition state seems to resemble a chair transition with the bonds across the centre of the two fragments appearing to cross over each other. So now the correct method is used, where for the central 4 carbon atoms (C13-C7-C10-C15) the dihedral angle is restricted to 0 degrees, then for atoms C13-C7-C10 the angle was limited to 100 degrees, this was repeated for atoms C7-C10-C15 (on the reactant molecule). Once this is completed for both the product and the reactant then the QST2 calculation proceeds again.

The boat transition state:

This optimised structure has an imaginary frequency at 840.15 cm-1, this final transition state for the boat conformer has an energy of -231.60 a.u.:

The boat transition state imaginary vibration: