Rep:Mod:chem2010b

Module 2 Inorganic Computational Laboratory

Olivia Highland

Introduction

In this exercise the computer programmes will be used to enable different conformers, their transition states and different thermodynamic and kinetic data. In order to model the different types of bonding in the inorganic molecules the IR, NMR and dipole moments can also be modelled which can demonstrate the electron density between the atoms.

BH3

The BH3 molecule has been drawn in Gaussview 5.0 and the different bond lengths were optimised. The Boron central atom was held in its position whilst B-H bonds were stretched to 1.5 Angstroms. When the optimisation came back the bond lengths for the B-H were shortened to 1.19349 Angstroms. In order to optimise the different bond lengths the distance between each of the nuclei is gradually decreased until the potential energy is at a minimum of the potential energy curve. Gradually the different optimisations are continued until all of the energies converge and the whole of the potential energy surface of the molecule has been traversed and the energy is at a minimum. It can be assumed that the minima has been reached when Gaussview measures the gradient of the graph as approximately zero, due to the use of the first derivative to calculate the gradient of the curve. The results of the MO optimisation for BH3 can be viewed via this link

Molecular Orbitals for BH3 with their energies:

Orbital picture of MO	Orbital from Gaussview	Orbital Type	Energies eV
		s orbital	-6.73054
		s orbitals	-0.51762
		py and s orbital mixing	-0.35679
		px and s orbital mixing	-0.35679
		pz non bonding	-0.07459
		px and s orbital anti-bonding	0.18855
		py and s orbital anti-bonding	0.18855
		s orbital anti-bonding	0.19183

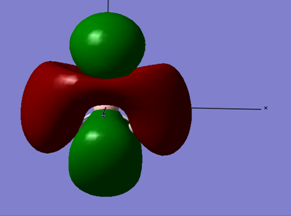
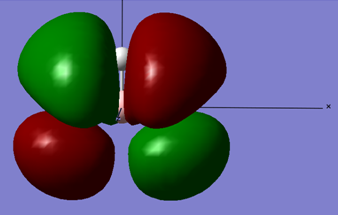
Below is the MO diagram as is predicted by Gaussview for BH3 if the simulated MO's for BH3 are used:

The different vibrations of BH3 are shown below:

Vibration
Frequency	1146.03 cm-1	1204.86 cm-1	1204.86 cm-1	2591.65 cm-1	2730.01 cm-1	2730.01 cm-1
Intensity	96.67	12.39	12.39	0.00	103.85	103.85
Symmetry	A2"	E'	E'	A1'	E'	E'

When the MO for the computed BH3 molecular orbitals is constructed, the energy levels for the 2e' and the 3a1' orbitals can either be constructed as is shown in the above MO diagram, or the levels can easily interchange and have the 2e' above the 3a1' MO levels. Either construction is viable.

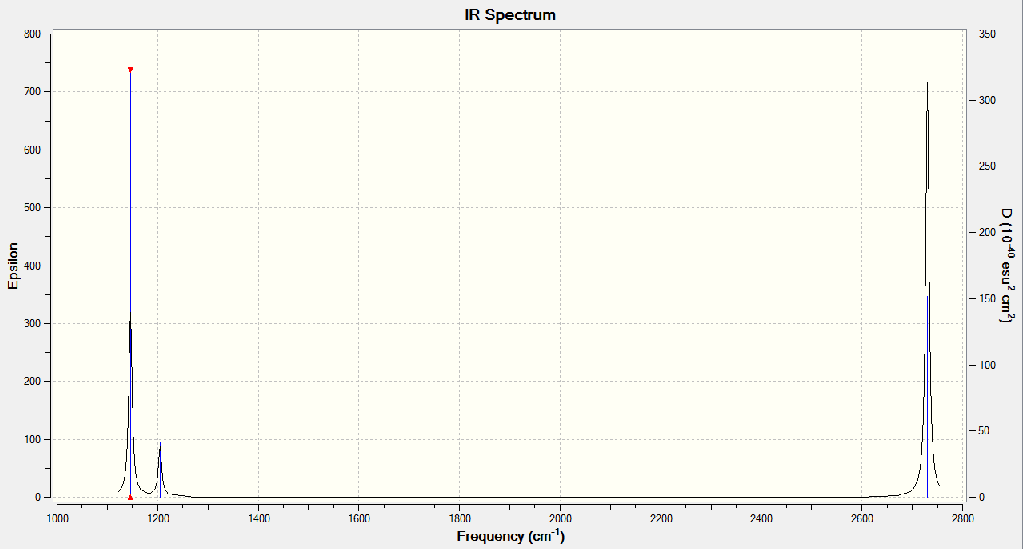
When the vibrational analysis is undertaken the second derivative of the wavefunction is performed we can confirm whether it is truly the minimum point or merely a different stationery point which could mean that the observed optimisation is truly the most stable conformation or just a transition state. When the IR spectrum is considered there are only 3 peaks when from the vibrational information we would be expecting 4 peaks. Although there are 6 total vibrations some are degenerate. Thus it can only be assumed that as the 2591.65cm-1 vibration has 0.00 intensity it is IR inactive and so does not show up on the spectrum.

The IR spectrum for BH3:

NBO analysis is also performed on the BH3 atoms, this NBO analysis splits the different electron density from the BH3 molecule and makes it resemble 2c-3e bonds. The log file then shows how the electron density is split between the different atoms. It also tells us how the different atoms have been hybridised and how much this hybridisation contributes. For example, from the first bond, there is 44.49% contribution of electron density from the Boron atom and 55.51% contribution from the Hydrogen atom:

NBO analysis, contributions from different orbitals:

The respective charges can be viewed for the different atoms in the BH3 molecule:

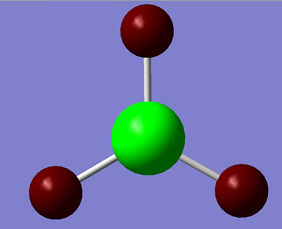
The respective charges can be viewed for the different atoms in the BH3 molecule:

We can see that as expected the electron deficient Boron is highly charged (green signifies a positive charge), and the Hydrogens atoms are negatively charged (red signifies negatively charged). The NBO charge for Boron is 0.331 and for the Hydrogens they are -0.110.

TlBr3

Computational simulations are useful when toxic chemicals need to be analysed. It is safer to manipulate and analyse the information provided about the compound from a computer simulation rather than handle the chemicals unnecessarily in the laboratory. However, as Thallium is a relatively large atom (much larger than Boron) it is necessary to use a larger basis set and also to use pseudo-potentials. Both the Bromine atoms and the Thallium atom give relativistic effects, due to the non-valence electrons which cannot be shown by using the Scrodinger equation on its own, this is why a pseudo-potential is required to replace these effects with a simpler model where the non-valence electrons are eliminated and only the valence electrons are considered. In this case the LANL2DZ basis set is used which is a medium sized basis set - shorter cpu time is preferred over greater accuracy. It uses D95V on the first row elements, but will then use Los Alamos ECP ( a pseudopotential) for the heavier metals.

The optimised bond lengths for the Tl-Br = 2.65095 angstroms

The optimised angle is 120 degrees between the Br-Tl-Br atoms.

The report summary for TlBr3:

File Type	.log
Calculation type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
E(RB+HF-LYP)	-91.21812851 a.u.
RMS Gradient Norm	0.00000090 a.u.
Dipole Moment	0.000 Debye
Point Group	D3H

The summary for the TlBr3 shows that the TlBr3 has been optimised as the Gradient has been normalised to approximately zero. It also describes which basis sets are being used and confirms the point group of the molecule. The optimised length for the Tl-Br bond is 2.65095 Angstroms. However, when this is compared with the literature value of 2.52 Angstroms it would seem as though the basis set used for the simulation is slightly inaccurate, however when the bond angle is optimised the structure agrees with all literature in providing a 120 degree bond angle between the Br-Tl-Br atoms, conforming to the predicted trigonal planar structure, this lack of complete accuracy is due to the fact that a better basis set would require longer computing time and would not improve the accuracy too greatly. The method used for the calculation is RB3LYP, the basis set that has been used is the LANL2DZ basis set which is appropriate for when the molecule under consideration contains atoms which are larger than Neon The optimisation can be viewed here The same basis set and method need to be used for both calculations so that it can be seen whether the molecule is actually at a minimum instead of at a transition point. Also if both calculations use the same method and basis set the values gained and energies produced can be compared. When different basis sets are used vastly different energies will be produced.

The low frequencies for TlBr3 are:

-3.4213 cm-1	-0.0026 cm-1	-0.0004 cm-1	0.0015 cm-1	3.9367 cm-1	3.9367 cm-1

These low frequencies are all taken from the output file from the optimisation of TlBr3. These 6 vibrations are the vibrations derived from the vibrations from the center of mass of the molecule and as they are much smaller than the smallest actual vibration of the molecule which occurs at 46.4289 cm-1; in addition to this the values are all close to zero so the basis set used can be assumed to provide a very accurate representation of the molecule. The lowest 'real' normal mode is is the same as the first frequency in the second row of the low frequency analysis in the output file. This vibration should be the same as the lowest vibration. Therefore in the Thallium Bromide complex the lowest 'real' mode is 46.4289cm-1.

Occasionally the bonds will disappear upon optimisation because Gaussview uses bond lengths that have been saved into the programmes memory. However, the problem with using these bond lengths is that the bond lengths that have been stored are mainly sourced from different organic molecules. Organic molecules tend to have shorter bond lengths than in inorganic molecules. Thus, when the programme tries to simulate the inorganic bond lengths they appear outside the known range and so they seem to have disappeared.

A bond is a region of electron density between two atoms which overlap in a constructive way, the greater the orbital overlap then normally the greater the strength of the bond.

Molybdinum Isomers

In this section the cis and trans isomers of Mo(PCl3)2(CO)4 are compared in an attempt to represent the Mo(PPh3)2(CO)4 isomers which were created and examined in the second year during synthesis labs. In the examples the phenyl groups have been replaced by chlorine groups. This is so that the computing time can be reduced and the results will still be similar as the large chlorine atoms are still sterically large and represent the Phenyl groups well. In this section the information will be used to evaluate the different isomers thermodynamic and kinetic properties.

Comparing the different molecules:

CIS	TRANS

For the cis isomers the literature bond lengths and bond angles vary as follows:

Structure	Literature Bond Length (Angstroms)/ Bond Angle (degrees)	Optimised Bond Length (Angstroms) / Bond Angle (degrees)	Difference (Angstroms)/(degrees)
Mo-P bond length	2.577	2.512	0.065
P-Mo-P bond angle	104.62	94.17	10.45
P-Mo-C(1) bond angle	163.7	176.09	-12.39
P-Mo-C(2) bond angle	80.6	82.22	-1.62
Angle between Cis CO ligands	83.0	87.07	-4.07
Angle between Trans CO ligands	174.1	178.4	-4.3

The Mo-P bond length is fairly accurately modelled compared to the literature, with a minimal difference between the simulated and the length gained by x-ray crystallography. The bond angles however for the cis complex are different; the P-Mo-P bond angle is less than the literature, this is because the literature has PPh3 ligands rather than PCl3 ligands. The PPh3 ligands would be larger and thus take up more space, forcing the P-Mo-P bond to be larger. The P-Mo-C angles are larger than in the literature as the PCl3 groups force the C=O ligands further around the axis.

Structure	Literature Bond Length (Angstroms)/ Bond Angle (degrees)	Optimised Bond Length (Angstroms) / Bond Angle (degrees)	Difference (Angstroms)/(degrees)
Mo-P bond length	2.577	2.512	0.065
P-Mo-P bond angle	104.62	94.17	10.45
P-Mo-C(1) bond angle	163.7	176.09	-12.39
P-Mo-C(2) bond angle	80.6	82.22	-1.62
Angle between Cis CO ligands	83.0	87.07	-4.07
Angle between Trans CO ligands	174.1	178.4	-4.3

The P-Mo bond length is very close to the exact literature value, this suggests that the simulation that is run is accurate. The other bond angles are also similar and are the same as the values that would be expected with most octahedral geometries. The only value which differs greatly is that of P-Mo-C which has a literature value of 87.2, even this is only 3 degrees from ideality. The bond length for P-Mo is shorter in the trans complex than it is in the cis complex, this could be because in the cis geometry the bonds are lengthened in order to minimise any interactions between the Phosphorus ligands as they are much closer in space than in the trans geometry

The report summary for the cis Molybdinum complex:

File Type	.log
Calculation type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
E(RB3LYP)	-623.57707196 a.u.
RMS Gradient Norm	0.00000303 a.u.
Dipole Moment	1.3108 Debye
Point Group	C1

The report summary for the trans Molybdinum complex:

File Type	.log
Calculation type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
E(RB3LYP)	-623.57592942 a.u.
RMS Gradient Norm	0.00002367 a.u.
Dipole Moment	0.0428 Debye
Point Group	C1

The energies for the different complexes are essentially the same when this is considered in terms of Hartrees, However, the values for the energies in kJ/mol are for the cis = -1637201.73 kJ/mol and for the trans = -1637198.73 kJ/mol, The trans complex is core stable by exactly 3 kJ/mol as is predicted in the literature and confirms that the thermodynamically more stable isomer is the trans isomer. The fact that this is the minimum energy for each of the conformations can be confirmed because in each complex the RMS gradient norm is approximately zero. The cis conformation is thermodynamically less stable because there is severe steric hindrance between the Phosphorus groups which are attached to the Molybdinum metal centre. These steric interactions increase the energy of the molecule. However, with the trans isomer, this is no longer a problem as the phosphorus groups can no longer interact with each other and their interactions with the equitorial carbonyl ligands are minimised from being axial. The differences that could be made to the PR3 ligands which could alter the stability of the isomers is whether the R groups are changed from Phenyl to smaller groups such as Methyl or simple PH3 groups, this would minimse the steric hindrance and thus lower the overall energy of the isomer, potentially making the cis isomer thermodynamically more stable than the trans - as there is minimal steric hindrance in the trans isomer, even with PPh3 ligands.

After the trans isomer had been optimised, the frequencies were then simulated. However, when the output files were returned from SCAN, the frequencies had not been fully optimised. It is because of this that there is a single negative frequency for the trans isomer:

Frequency = -4.32 cm-1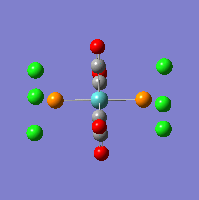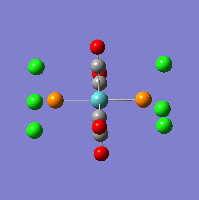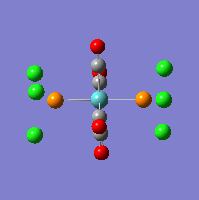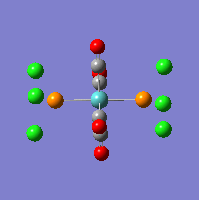

The vibration shows that the negative frequency corresponds to a twisting of the P-Cl ligands. The only explanation that can be given for this negative energy level is that for the frequency the molecule has not been fully optimised to its lowest energy (as has been stated from consideration of the output file) and that a transition state is being observed rather than the fully optimised molecule. This would explain any differences between the vibrations calculated for this molecule and the literature vibrations for the molecule.

The IR spectrum for the trans isomer.

The different IR vibrations for the trans complex are as follows:

Frequency (cm-1)	Type	Experimental (cm-1)
436.17	CO bend all 4 ligands	-
437.33	CO bend all 4 ligands	-
483.45	CO bend	-
523.16	CO bends (all 4 ligands synchronised)	-
1950.22	Trans CO stretch	1842.16
1950.96	Trans CO stretch	1889.81
1977.04	All 4 CO stretch	1901.12
2030.0	All 4 CO stretch	2013.23

Some of the vibrations for the CO bonds (bends) are in the fingerprint region and so do not show up on the IR spectrum.

The IR spectrum for the cis isomer.

The different IR vibrations for the cis complex are as follows:

Frequency (cm-1)	Type	Experimental (cm-1)
396.27	Axial CO vibration	-
514.14	CO bend	-
563.76	Equitorial CO bend	-
1945.31	Equitorial CO vibration	1892.20
1958.36	All 4 CO's vibrating	-
2023.31	All 4 CO's vibrating	-

Neither of the molybdinum complexes fully optimised upon computing the frequency calculation; thus it can only be assumed that as in the cis frequency calculation there were no negative frequencies and there was only one negative frequency for the trans isomer that in both instances a transition state is viewed rather than the absolute minimum energy conformer. In terms of the frequency this means that the frequencies that are observed from the simulations will alter slightly from the literature and the values found from the second year synthesis labs: the vibrations are approximately 50cm-1 off of the experimental values for the cis complex. It is to be expected that there would only be one peak for the trans compound because there is more symmetry in the molecule and so fewer different vibrations. However with the cis compound there are 4 different predicted peaks because of the lower symmetry in the molecule. In the IR spectrum for the cis complex the literature and the second year synthetic lab data suggests that there should only be one peak, from the data it would suggest that 4 peaks are expected. However, only one peak appears on the spectrum, which suggests that all the peaks merge into each other. For the trans isomer the four stretches are observed which agrees with the prediction of 4 peaks. The differences between the experimental values and the simulated values vary greatly from approximately 100cm-1 to approximately 15cm-1.

Mini Project: Tebbes Reagent

The Tebbes Reagent is an organometallic compound used in the methylation of carbonyls. Tebbes reagent itself (with the structure used in the rest of this project) does not react with the carbonyls, instead it needs to first be reacted with a mild lewis base, once this has been achieved then the product of this reaction Cp2TiCH2 reacts with the carbonyls in a reaction similar to the Wittig reaction.

In this project a variation on Tebbe's reagent will be considered. Tebbe's reagent has the following structure:

However, in order for it to be successfully modelled then the structure needs to be altered so that the Cp rings are mow replaced with Chlorine atoms. The Chlorine atoms are appropriate substitutes for the sterically hindered cyclopentadiene rings as they are large atoms however with less atoms in the molecule the calculations should have a shorter computing time, instead the structure that is used in all the calculations is as follows:

Tebbes reagent, literature bond lengths from X-ray crystallography.

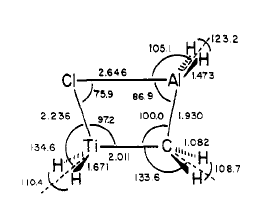
In this project the aim will be to see what happens to the bridging bond lengths when the bridging ligands are exchanged with the terminal ligands. The next two structures that will be optimised are:

The calculation methods used for these calculations are UB3LYP, the basis set that is used for the calculations is LANL2DZ, this basis set was chosen because it is used when there are heavier elements in the molecule and as the molecule contains Ti, Al and 3Cl atoms. So to get the most accurate results a good basis set needs to be used.

When the modified Tebbes reagent is optimised the bond lengths calculated by the optimisation are as follows:

Structure	Literature Bond Length (Angstroms)/ Bond Angle (degrees)	Optimised Bond Length (Angstroms) / Bond Angle (degrees)	Difference (Angstroms)/(degrees)
Al-bridging C bond length	1.93	2.19	-0.26
Al- bridging Cl bond length	2.65	2.52	0.13
Ti-bridging Cl bond length	2.24	2.39	-0.15
Ti-bridging C bond length	2.01	2.26	-0.25
Cl-Al-C bond angle	86.9	95.7	-8.8
Al-C-Ti bond angle	100.0	88.3	11.7
C-Ti-Cl bond angle	97.2	97.7	-0.5
Ti-Cl-Al bond angle	75.9	78.3	-2.4

Energy kJ/mol	(1) = -590475	(2) = -590475	(3) = -655587

These energies show that Structure 1 and structure 2 have the same energy and are as stable as each other. However, unusually, the structure 3 has the most negative energy as the structure is under less strain.

When the bond lengths and the bridging bond angles are compared with the literature it is clear that the bond lengths are fairly accurate with minimal difference between the computed lengths and the literature values. The main differences between the structures come from the internal bond angles; especially the Cl-Al-C and the Al-C-Ti bond angles. In this simulation the Cl-Al-C bond angle is actually larger than for the literature. This may be because in the literature for the Tebbe's reagent Cp rings are used as the outer ligands rather than Cl atoms. These Cp ligands would alter the shape of the central bridging region considerably. Without these the conformation is much less sterically hindered. Thus the Cl-Al-C bond is much larger. The Al-C-Ti bond is actually smaller than the literature when it was computed. This may be because in the literature the Tebbe's reagent structure has a CH2 bridging ligand rather than CH3, thus the bonds are not forced apart as much in the literature, creating a larger Al-C-Ti bond angle.

When the structures of the 'original' Tebbes reagent is changed then many different changes occur to the structure. The central bridging region has a large change in the internal angles. For Structure (2) the bridging region is a perfect diamond. The Al-Cl and the Ti-Cl bonds all even out to be 2.47 Angstroms. The Cl-Ti-Cl angle is 85 degrees, as is the Cl-Al-Cl angle. The Al-Cl-Ti and the Ti-Cl-Al bond angles are identical at 95.2 degrees. I would have expected this change to the central region to have continued when the Chlorine atoms are replaced by CH3 groups. The central bridging Al-Cl and Ti-Cl bonds have all evened out to 2.47 Angstroms, this has shortened the original Tebbes reagent computed Al-Cl bond lengths (2.52 Angstroms) and has increased the Ti-Cl bond length from 2.39 Angstroms.

It would be expected that this diamond shape for the bridging region would occur again. However, this does not happen, instead the angles became even more distorted than in the original molecule. The C-Al-C internal angle became 111 degrees, the Al-C-Ti became 77 degrees, the C-Ti-C angle changed to 94 degrees and the and the Ti-C-Al angle became 72 degrees. This is because in the third molecule attached to the Aluminium are two Chlorine atoms, as these are perpendicular to the central region. As these need to be widely spread out from each other as their charges repel each other the other tetrahedrally bonded CH3 groups must become more spread out, thus increasing the internal angles. The C-Ti-C internal angle for structure (3) has decreased slightly than in the original molecule, because originally there were two chlorines attached to the Titanium, now there is only one so there is slightly less repulsion between the groups.

Molecular Orbitals

The following shows the molecular orbitals for the first Tebbes reagent:

Molecular Orbitals for BH3 with their energies:

MO energy Level	Orbital from Gaussview	Orbital Type	Energies eV
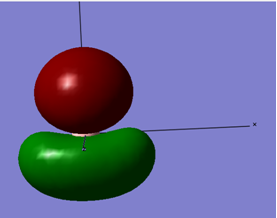
LEVEL 16		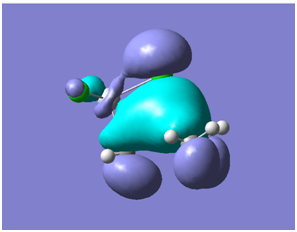All bonding interactions within the bridging region	-0.433
level 17		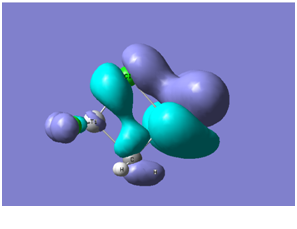Interesting bonding interactions between the Cl and the CH3 bridging bonds.	-0.409
HOMO		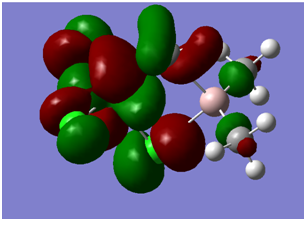Antibonding orbitals focussed more on the Ti side of the molecule	-0.264
LUMO		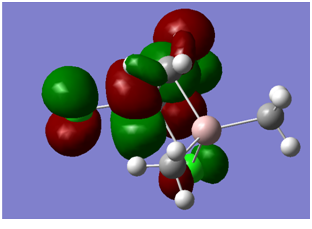Antibonding d and p orbitals, purely on the Ti side of the molecule	-0.140
LUMO +1		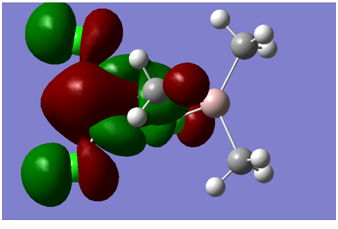All antibonding orbitals, but orbitals are becoming more diffuse	-0.129
LEVEL 27		Shows a pi bond which has been confirmed by the literature, showing that the optimisation is accurate.	-0.345

These MO diagrams are interesting because in level 16 there is a large region of bonding interactions within the bridging region, which shows that this area of the molecule is quite stable, its stability can be put down to the strong Ti-Cl bonds and Al-C bonds all this is added to by the back donation from the Cl into the Al empty orbital. In level 17 there is interesting bonding again when there appears to be electron density flowing from the Ti-Cl to the Ti-CH3 bond; there is also the expected back donation from the Cl to the Al visible in the molecular orbitals. In the HOMO all the antibonding orbitals are on the Ti side, which is what we would expect as the Tebbes reagent is easily changed into the Cp2Ti=CH2 by a Lewis base in order to react with different carbonyls. This is also shown in the LUMO orbital, explaining why the molecule changes so easily as the orbitals in the HOMO-LUMO region are focused mainly on the Ti side of the molecule. Level 27 shows the same pi orbitals as are discovered in the reference confirming the correct structure has been formed:

Vibrations

The different vibrations were calculated using the same basis set and pseudopotential. With the 'original' molecule the Ti-Cl bridging stretch is a higher frequency than in structure (2) where both bridging molecules are chlorines, the difference in frequencies are approximately 40cm-1.

The different vibrations for the Tebbes Reagent are as follows:

Vibrations
Frequency / cm-1	317.00	346.68	410.01	421.58
Vibration Shown	Bridging Ti-Cl stretch	Bridging Al-CH3 stretch	Ti- all chlorines stretch	Bridging Ti-CH3 stretch

The different vibrations for the Tebbes Reagent (2) are as follows:

Vibrations
Frequency / cm-1	274.71	284.32	413.03	587.42
Vibration Shown	Bridging Ti-Cl stretch	Bridging Al-Cl stretch	Ti- all chlorines stretch	External Ti-CH3 stretch

The different vibrations for the Tebbes Reagent (3) are as follows:

Vibrations
Frequency / cm-1	318.68	324.77	400.20	450.23
Vibration Shown	Bridging Al-CH3 stretch	Bridging Al-CH3 stretch	Bridging Ti-CH3 stretch	External Ti-CH3 stretch

When the frequency analysis was completed for the different molecules the second derivative that has been calculated upon the functions proves that all the different molecules have been fully optimised as there were no negative vibrations and all the lowest frequencies are close to zero:

Original Tebbes low frequencies:

-3.4874  | -1.3693 |  -0.0004 |  0.0001  |  0.0003  |  2.7282 ||

Second Structure low frequencies:

-3.9498 |  -3.2882 |  -3.1024  | -0.0003  |  0.0002  |  0.0005 ||

Third Structure low frequencies:

-0.0003  | -0.0002  |  0.0006  |  4.1681  |  5.7846  |  6.2343 ||

The different vibrational frequencies for the bridging ligands confirm the ordering of the stability of the bonds. For structures 1 and 2 the vibrations for the Ti-Cl bridging ligand are 317cm-1 and 274.17cm-1. This suggests from the E=hf equation that the structure 1 has stronger Ti-Cl bonds than for structure 2, this is because greater stability is given to structure 1 from the CH3 bridging ligand. However, structure 3 is the most stable as the bridging Ti-CH3 are the strongest bonds, giving stability to the overall molecule, this is confirmed by the energies as discussed above.

Conclusion

To conclude, in this module Gaussview has been used to model different inorganic molecules and compare them against the literature. In the BH3 section it was seen that the bonds lengths all agree well with the literature and the MO's that are generated fit well with the recognised MO diagram. The NBO analysis is also accurate with respect to predicting the charges on the BH3 molecule with a slightly positive charge on the Boron and a negative charge on the Hydrogen. For Thallium the structure was again optimised correctly. For the Molybdinum complex the simulations were run between two different isomers, the energies produced confirmed the trans is the most stable conformer because of the symmetry within the molecule and the lack of interactions between the ligands. The IR spectra that came back also showed that the predicted number of peaks for each molecule were correct as some vibrations were IR inactive and some were degenerate. The values were slightly different when compared with the experimental values as the structures were not completely optimised. For the mini project Tebbes Reagent was chosen as the subject to be analysed and to see what would happen if the bridging ligands were exchanged with the non bridging ligands. This provided a more stable structure when the bridging ligands were all changed to be CH3 instead of CH3 and Cl or two Cl bridging ligands. The MO's when analysed showed that the structure would be prone to attack by a Lewis Base. When the frequencies were analysed it became clearer that the more stable bonds were Ti-C and Al-C rather than Ti or Al-Cl, this was because they had a higher frequency and thus required more energy to vibrate and so are more stable. All of the molecules for the mini project were confirmed as being at a minimum.