Rep:Mod:chchanmod2

Introduction

Besides basic organic hydrocarbon molecules, computational models can also apply to inorganic molecules, such as metal complexes and solid lattices. These models can not only give an insight about its structural properties, but also its reactivity and physical properties. In this module, the structures are optimised by the application of density functional calculations to solve the Schrodinger's equation, which generates electronic wavefunctions with fixed positions of nuclei. Born Oppenheimer approximation, which states since electrons is so much lighter than nuclei, thus electrons move much faster than nuclei, hence electrons change their positions instantaneously to nuclei and so nuclei are stationary compare to electron movement, is taken into account during the calculations of electronic wavefunctions. The forces of the interactions between electrons and nuclei are calculated, and they are converted to energy; the minimum energy configuration (the optimised structure) is obtained by altering the positions of these nuclei. The model for calculations is based on potential energy curve, hence the minimum energy point is equivalent to the force of the system at equilibrium (the turning point of the surface) as shown in Figure 1. The stationary point is determined by the root mean squared gradient, which is the rate of change of energy calculated with respect to the distance between nuclei. The quantum mechanic approach and the minimal basis set are the keys determining the accuracy of the calculations.

Figure 1 - Potential Energy Curve

The zero root mean squared gradient can only indicate the presence of a stationary point, but it has no information regarding the nature of the turning point. At a minimum point, any atomic motion would result in a higher energy state; in contrast, a lower energy state causes by atomic motion would occur at a maximum point. Thus vibrational analysis can be applied to distinguish between them, as a positive vibrational frequency indicates a minima whereas a maxima would have a negative vibrational frequency. It is important to keep using the same calculation method with the same basis set during the frequency calculations as applied to the optimisation, this is because the optimised structure is not necessarily a minimum point of the potential energy curve under other calculation methods or basis sets, which would give unreliable frequency estimations, hence same method and basis set must be kept for any estimations for the particular optimised structure.

Figure 2 - Potential Energy Curve with Two Turning Points

Simple Main Group Compound - Borane

Optimisation

The first molecule being investigated is a borane, which is a trigonal planar under the D_3H point group. The molecule was being input into GaussView and each B-H bond length was set to be 1.5 Å. Via the application of the B3LYP method with the 3-21G basis set, the molecule was optimised to give all H-B-H bond angles at 120^o and all B-H bond lengths at 1.19Å. The experimental B-H bond length in BH₄^- is 1.25Å, hence they are in good agreement. The important results summary is shown in Table 1 and the log file for the optimisation can be accessed at Media:BH3_OPTIMISATION_chc08.LOG.
Root mean squared (RMS) gradient is much less than 0.001, which is an indication of the high level of accuracy achieved by this model; whilst the short time taken for the completion of the calculations indicates the simplicity of the model.

Table 1 – Result Summary of BH3 Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set 3-21G E(RB+HF-LYP) -26.46 Hatrees RMS Gradient Norm 0.00000285 Dipole Moment 0.0000 Debye Point Group D3H Job Time 91 seconds 3-D Structure

As mentioned in the introduction, the model finds turning points by altering the position of nuclei; for this particular molecule, the boron atom is fixed and the optimised structure was found by reducing the B-H bonding distance via changing the H atoms positions as shown in Figure 3. From the first three frames Figure 3, the B-H bonds cannot be seen, but this does not imply that the bond does not exist. This is a limitation of GaussView, as the graphical interface compares bonds with their relative average bond lengths and if they differs too much, it would not display them. A bond is a description of the interactions between two nuclei, it can be mainly classified into ionic and covalent bonds. Ionic bond arises from the Coulombic attraction between ions of opposite charges, whilst covalent bond describes the electron density present in the bonding molecular orbital formed by the overlap of atomic orbitals of the atoms. Although bonding distance would affect the bonds, but using only bond distance to describe a bond is clearly insufficient, and hence orbital interactions should be taken into account in the description of bonds. Figure 3 - BH3 Optimisation Procedure.

Figure 4 - Change of Total Energy of the Molecule when Hydrogen Nucleus Positions are Altering.

Figure 5 - Change of RMS Gradient when Hydrogen Nucleus Positions are being Altered.

Figures 4 and 5 reflect the optimisation procedure, the position of Hydrogen atoms would continue to be changed until the RMS gradient reaches zero, hence a turning point. Although this indicates a stationary point, but whether it has converged to a minimum or maximum requires further analysis, thus vibrational analysis was performed.

Vibrational Analysis

Table 2 shows the 6 vibration modes which can be performed by the molecule, all the frequencies obtained are positive, hence the optimised energy/structure is at the minimum point of the potential energy curve. The log file is at Media:BH3_FREQUENCY_chc08.LOG.

Table 2 – Vibrational Frequencies of BH₃ molecule.

Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode	Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode
1146	93	A2’’		1205	12	E’
1205	12	E'		2592	0	A1’
2730	104	E’		2730	104	E’

The A1’ atretch at 2592 cm-1 is infra-red inactive, as it would not cause a dipole moment on the molecule due to its symmetric stretching, hence it would not show on its infra-red spectrum (as shown in Figure 6). Vibrational analysis can also be used as a tool to investigate if the method applied is accurate enough. Besides the infra-red vibrations, GaussView would also estimate the frequencies caused by the translation of the whole molecule without bond distortion termed 'low frequenices' in the log file. These frequencies are -0.3716, -0.0098, -0.0018, 37.2444, 37.9574 and 37.9592 cm-1, the better the method employed the closer to zero these frequencies should be, generally the acceptable range is -10 to 10 cm-1. For this particular model of BH3, the lowest wavenumber is 1146 cm-1 whilst the largest low frequency is 38 cm-1, thus the magnitude of it is relatively small, hence despite using a low level method, it is still accurate enough for this simple molecule.

Table 3 – Result Summary of BH3 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set 3-21G E(RB+HF-LYP) -26.46 Hatrees RMS Gradient Norm 0.00004507 Dipole Moment 0.0000 Debye Point Group D3H Job Time 11 seconds

Figure 6 - Computed Infra-red Spectrum of BH₃ molecule.

Molecular Orbital Estimation

Molecular orbitals are generated by Linear Combination of Atomic Orbitals (LCAO) theoretically; as shown in Figure 7, the computed molecular orbitals agree with the theoretical approach (The coloured pictures in Figure 7 are the computed results). Based on the energies computed, it has clearly shown that the 1a1' molecular orbital is at a much lower energy level than any other molecular orbitals, which agrees with the theory as it is composed of the 1s orbital of Boron atom, whereas the others are formed by 2s and 2p orbitals of Boron atom with 1s orbitals of Hydrogen atoms. The model can compute most molecular orbital energies accurately, but for 2e' and 3a1', as they have very similar energies with only ~9 kJ mol-1 difference, it is very hard to estimate precisely their arrangement, thus a more accurate model needs to be applied to achieve a better results. As most reactions proceed via HOMO and LUMO interactions, HOMO can be seen clearly as one of two degenerate e' bonding orbitals, whilst the LUMO is the empty non-bonding pz orbital. This explains the Lewis acidity of the molecule as it can accept a lone pair of electrons at the LUMO and this would not have effect on the bond order as it is a non-bonding orbital. For BH3, there is no significant mixing, which can be more important in other molecules. The log file can be accessed at Media:BH3_MO_chc08.LOG Table 4 – Molecular Orbital Energies with their Symmetries Symmetry Energy (Hartree) Energy (kJ mol-1) 1a1' -6.73 -1.77 x 104 2a1' -0.52 -1.36 x 103 1e' -0.36 -9.37 x 102 1a2" -0.07 -1.96 x 102 2e' 0.19 4.96 x 102 3a1' 0.19 5.05 x 102

Figure 7 - Molecular Orbital Diagram of BH3 molecule.

Natural Bond Orbitals

Natural Bond Orbital is a representation integrating both atomic and molecular orbitals, it shows the nature of bonds and the charge distribution among a molecule. The BH₃ molecule is composed with an electron deficient Boron centre, surrounded by electron rich Hydrogen atoms; whilst the charge distribution is calculated as +0.33 at Boron atom and -0.11 at each Hydrogen atom, giving an overall neutral molecule. Figure 8 shows that all the bonds are two centres-two electrons (2c-2e) bond, with 44.48% Boron and 55.52% Hydrogen contributions to the total electron density. The results also show that the Boron centre comprises of 33.33% s-character and 66.67% p-character, whilst each Hydrogen atom has 100% s-character. This implies that Boron uses three sp² hybridised orbitals for bonding as described with Valance Shell Electron Pair Repulsion(VSEPR) theory. The "lone pair" orbital with 100% p-character centred at Boron indicates the presence of a non-bonding p orbital, which is the LUMO as mentioned previously. In addition, the calculations show there is a 100% s-character orbital at the Boron centre, which is the 1s orbital and it would not interact with other orbitals as it is too low in energy compare to the H₃ fragment molecular orbitals.

Figure 8 - Indication of Electron Rich and Electron Deficient Centres by Red and Green Respectively.

Figure 9 - Charge Distribution Among BH3 Molecule.

Larger Main Group Compound - Thallium Tribromide

Optimisation

The same computational model used for BH3 can also applied for TlBr3, since they are both trigonal planar under the D3H point group, but it would be less accurate as there are many more electrons need to be taken into account, thus pseudo potential was applied to give a more accurate optimisation. Psedo potential improves the approximation by including relativistic effects imposed on distant valence electrons. Besides chosing the method and basis set, the point group symmetry was constrained to D3H along with tightening the toleration to 0.0001 to impose strict rules for the convergence; since the RMS gradient is much less than 0.0001, hence the optimisation was successdul and it is of high level of accuracy. The optimisation gives all Tl-Br bond lengths at 2.65Å and all Br-Tl-Br bond angles at 120o. The experimental Tl-Br bond length was measured to be 2.51Å, thus the values are still in roughly good agreement, but it can be improved by a more accurate calculation method. The log file can be accessed at Media:TLBR3_OPTIMISATION_chc08.LOG Figure 10 - Optimisation Procedure of TlBr3.

Table 5 – Result Summary of TlBr3 Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set LANL2DZ E(RB+HF-LYP) -91.22 Hatrees RMS Gradient Norm 0.00000095 Dipole Moment 0.0000 Debye Point Group D3H Job Time 27 seconds 3-D Structure

Figure 11 - Change of Total Energy during Optimisation.

Figure 12 - RMS Gradient Measurement during Optimisation.

Vibrational Analysis

Table 6 shows the vibrational frequencies computed for TlBr₃, all the frequencies are positive values, which confirm the optimised structure is at the minimum point of the potential energy curve. The log file can be accessed at Media:CHC_TLBR3_FREQ.LOG
There is one infra-red inactive mode of vibrations as BH₃, the symmetric stretch has zero intensity since it does not generate a dipole moment.

Table 6 – Vibrational Frequencies of TlBr₃ molecule.

Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode	Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode
46	4	E'		46	4	E’
52	6	A2’’		165	0	A1’
211	25	E’		211	25	E’

The low frequencies calculated are -3.4213,-0.0026,-0.0004,0.0015,3.9367 and 3.9367 cm-1, which are quite close to zero and their magnitudes are small in comparison with the lowest wavenumber, 46 cm-1; this shows that the method chose was accurate enough for this particular molecule. There is a large difference in the energies of the vibrations of TlBr3 and BH3(Figure 6 and 13), which can be explained by bond strength, as B-H bond is much stronger than Tl-Br bond as atoms involved are smaller and have higher surface charge densities. From orbital overlap perspective, the orbitals involve in B-H bonds are similar in size, which would give better orbital overlap, hence a strong bond; whereas the orbitals of Tl is much larger than those of Br giving a poor overlap of orbitals, thus a week bond. A strong bond requires more energy to stretch therefore would be at a higher wavenumber.

Table 7 – Result Summary of TlBr3 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set LANL2DZ E(RB+HF-LYP) -91.22 Hatrees RMS Gradient Norm 0.00000088 Dipole Moment 0.0000 Debye Point Group D3H Job Time 11 seconds

Figure 13 - Computed Infra-red Spectrum of TlBr₃.

Geometric Isomerism of Mo(CO)₄(PCl₃)₂

Introduction

There are different kinds of isomerism such as linkage isomerism, optical isomerism, and they appear habitually in molecules, especially transition metal complexes; these isomerisms would affect not only the physical and chemical properties of the molecule, but also its spectroscopic properties. In this section, the geometric isomerism of Mo(CO)₄(PCl₃)₂ would be investigated.

Figure 14 - Geometric Isomers of Mo(CO)₄(PCl₃)₂.

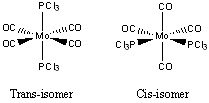
Optimisation

Loose Optimisation

Both isomers were firstly optimised by the B3LYP method with the basis set and pseudo-potential, LANL2MB, which is a low level method, hence loose convergence was imposed to ensure turning points for both structures would be found. The trans-isomer does not possess a dipole moment, which is the same as the BH₃ and TlBr₃, due to the cancellation of dipole moment in all directions, whereas a dipole moment would be expected in the cis-isomer. This observation is under the assumption of PCl₃ acts as an atom, L, hence no P-Cl bond exists. The difference between energies of the two isomers is relatively small, as the energy of cis-isomer is -1.621312 x 10⁶ kJ/mol, whilst for trans-isomer it is -1.621304 x 10⁶ kJ/mol, giving about 8 kJ/mol difference and cis-isomer is thermodynamically slightly more stable. This low energy barrier suggests the possibility of interconversion between the two isomers under this model. Both molecules were computed to have C₁ symmetry, which is not true since trans-isomer has higher degree of symmetry.

Table 8 – Result Summary of Cis-Mo(CO)4(PCl3)2 Loose Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set LANL2MB E(RB+HF-LYP) -617.53 Hatrees RMS Gradient Norm 0.00001957 Dipole Moment 8.6315 Debye Point Group C1 Job Time 21 minutes 55 seconds 3-D Structure

Table 9 – Result Summary of Trans-Mo(CO)4(PCl3)2 Loose Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set LANL2MB E(RB+HF-LYP) -617.52 Hatrees RMS Gradient Norm 0.00005520 Dipole Moment 0.0000 Debye Point Group C1 Job Time 4 minutes 16 seconds 3-D Structure

The RMS gradients for both optimisations are very small, which indicate stationary points were being found, but these can be fake minimums as there might be more than one turning points on the potential energy curves of the molecules as suggested in Figure 15. Based on this possibility and the fail of assigning symmetry of this model, a tighter optimisation is required in order to improve the results. The log file for cis and trans-isomer loose optimisation can be accessed at Media:Cis_optimisation_1_chc08.out and Media:Trans_optimisation_1_chc08.out respectively.

Figure 15 - Possible Potential Energy Curve for the Isomers.

Tight Optimisation

To perform a tighter optimisation, the same B3LYP method was applied but with LANL2DZ pseudo-potential and basis sets, also the electronic convergence was increased. In addition, the torsion angles were modified according to Figure 16 before the calculations. The optimised energies for cis- and trans-isomer are -1.637201 x 106 kJ/mol and -1.637198 x 106 kJ/mol respectively, which shows that there is about 3 kJ/mol difference, as loose optimisation, the cis-isomer is slightly more stable than trans-isomer thermodynamically; since the energy difference is even smaller than that obtained from loose optimisation, therefore based on the energies calculated by optimisations, the conclusion of whether cis or trans isomer is more stable cannot be drawn. The point groups of the tight optimisations are still C1, hence application of LANL2DZ is not enough to improve the optimisation results. The trans-isomer obtained from tight optimisation possesses a dipole moment, which differs from the one from loose optimisation; this suggests during the tight optimisation, the P-Cl bond has started to be taken into account. The log file for cis and trans-isomer tight optimisation can be accessed at Media:Cis_optimisation_2_chc08.out and Media:Trans_optimisation_2_chc08.out respectively.

Figure 16 - Modification of the Torsion Angles of the Isomers.

Table 10 – Result Summary of Cis-Mo(CO)4(PCl3)2 Tight Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set LANL2DZ E(RB+HF-LYP) -623.577 Hatrees RMS Gradient Norm 0.00004388 Dipole Moment 1.3062 Debye Point Group C1 Job Time 38 minutes 56 seconds 3-D Structure

Table 11 – Result Summary of Trans-Mo(CO)4(PCl3)2 Tight Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set LANL2DZ E(RB+HF-LYP) -623.576 Hatrees RMS Gradient Norm 0.00000083 Dipole Moment 0.3044 Debye Point Group C1 Job Time 111 minutes 17 seconds 3-D Structure

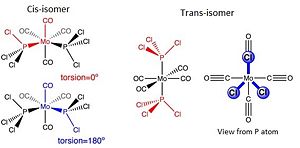Geometric Parameters and Theoretical Prediction of Stability

As seen in Table 12, all the bond lengths and bond angles are in good agreement with the literature values, since the exact compounds could not be found, thus similar molecules were used. The cis-isomer literature values were based on cis-Mo(CO)₄(PMe₂Ph), whilst trans-Mo(CO)₄PPh₃ was used for comparison.

Table 12 – Comparison between Computed Results and Literature Values.

	Cis-isomer	Cis-isomer Literature	Trans-isomer	Trans-isomer Literature
Mo-P Bond Length /Å	2.51	2.53	2.48	2.50
Mo-C Bond Length /Å	2.01 and 2.06	1.98 and 2.02	2.11	2.01
P-Mo-P Bond Angle /o	94.2	94.8	180	180
P-Mo-C Bond Angle /o	89, 92 and 176	88, 94 and 176	89 and 91	87 and 92
C-Mo-C Bond Angle /o	87, 89, 90 and 178	88, 90, 93 and 177	90 and 180	92 and 180

As PCl₃ is a medium group, therefore some steric effects would be expected in the cis-isomer, which would destabilise the isomer. Although steric effects is important, but electronic effects also need to be considered. For the cis-isomer, a trans-effect is present between the P atom and CO group to stabilise the molecule; the non-bonding orbital at P can interact with the π* orbital of CO to form two new molecular orbitals to enhance stabilisation. Thus it is hard to predict whether steric effects or electronic effects would affect the molecule stronger.
By changing the substituents around P atom, the stability of geometric isomers can be altered. To achieve a more stable trans-isomer, a very bulky group such as PPh₃ can be used as substituent to maximise the steric effects; Alternatively, if a cis-isomer is more stable, it would have small and electron-donating substituent, such as CH₃, to minimise the steric effects and maximise the electronic effects.

Vibrational Analysis

Minimum Stationary Point Justification

To further confirm the stationary points found during the optimisations are at their minimums, vibrational analyses were carried out. All the vibrational frequencies calculated are positive illustrating the optimised structures are at the minimum stationary points of their respective potential energy curves. The log files of cis- and trans-isomer frequency calculations can be accessed at Media:Cis_frequency_chc08.out and Media:Trans_frequency_chc08.out respectively.

Table 13 – Result Summary of Cis-Mo(CO)4(PCl3)2 Frequency Calculations. Calculation Type FREQ Calculation Method RB3LYP Basis Set LANL2DZ E(RB+HF-LYP) -623.577 Hatrees RMS Gradient Norm 0.00004406 Dipole Moment 1.3062 Debye Point Group C1 Job Time 28 minutes 45 seconds

Table 14 – Result Summary of Trans-Mo(CO)4(PCl3)2 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set LANL2DZ E(RB+HF-LYP) -623.576 Hatrees RMS Gradient Norm 0.00000093 Dipole Moment 0.3044 Debye Point Group C1 Job Time 28 minutes 43 seconds

The low frequencies of cis-isomer are -1.9993, -0.0003, 0.0004, 0.0005, 0.8168 and 1.2763 cm^-1, whilst for trans-isomer, they are -2.1478, -1.5103, 0.0004, 0.0005, 0.0005 and 3.4585 cm^-1. All these are very close to zero, which indicates it is an acceptable method to compute these compounds.

Vibrations at Low Energies

On the computed infra-red spectra as shown in Figure 17 and 18, there are peaks at very low wavenumbers; these are corresponded to the weak Mo-P bond stretches, and they would general happen at room temperature (normally less than 207 cm^-1. This is one of the reasons why GaussView failed to predict the correct point group of the molecules, as the P groups can rotate freely around the Mo metal centre.

Table 15 – Selected Low Vibrational Frequencies of cis-Mo(CO)₄(PCl₃)₂ molecule.

Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode	Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode
11	0.03	A		18	0.01	A
42	0.00	A		44	0.10	A
56	0.83	A		67	0.22	A

Table 16 – Selected Low Vibrational Frequencies of trans-Mo(CO)₄(PCl₃)₂ molecule.

Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode	Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode
5	0.09	A		6	0.00	A
37	0.42	A		40	0.31	A
72	0.00	A		79	1.07	A

Figure 17 - Computed Infra-red Spectrum of the Cis-isomer.

Figure 18 - Computed Infra-red Spectrum of the Trans-isomer.

Carbonyl Stretches

Symmetry of a molecule would affect its spectroscopic data, therefore infra-red spectroscopy can act as a tool to identify geometric isomers like Mo(CO)₄(PCl₃)₂. The computed frequencies are illustrated in Table 17 and 18.

Table 17 – Vibrational Frequencies of Carbonyl Groups of cis-Mo(CO)₄(PCl₃)₂ molecule.

Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode	Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode
1945	762	A		1949	1500	A
1959	634	A		2024	597	A

Table 18 – Vibrational Frequencies of Carbonyl Groups of trans-Mo(CO)₄(PCl₃)₂ molecule.

Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode	Wavenumber (cm-1)	Intensity	Symmetry	Vibrational Mode
1950	1475	A		1951	1467	A
1977	1	A		2031	4	A

The computed results clearly differ from the literature values, which can be explained by the wrong symmetries of the computational models. The point group of the cis-isomer is C2V, whereas the trans-isomer is under the D4H point group. As the trans-isomer is of a high degree of symmetry, therefore there would be fewer different carbonyl stretches expected, which agrees with the literature (experimental) values. Since the computational model assigned the symmetry to be C1 (the lowest symmetry point group), therefore four different vibrational modes were computed. For the cis-isomer, as it has a lower level of symmetry, thus a few different carbonyl stretches would be expected, which again agrees with the literature values. The computational model correctly predicted 4 different stretches, but the symmetry and wavenumber of each stretch are different from the literature values. The computed stretches should have the following symmetries, 1950 cm-1 of B2, 1951 cm-1 of B1 and both 1977 and 2031 cm-1 are of A1. Alteration of the point group during optimisation can help to improve not only the optimisation results, but also the vibrational frequency estimations.

Table 19 – Literature Carbonyl Vibrational Frequencies of Mo(CO)4(PCl3)2. Cis-isomer Trans-isomer Wavenumber (cm-1) Symmetry Wavenumber (cm-1) Symmetry 1986 B2 1896 Eu 1994 B1 2004 A1 2072 A1

Mini Project - Structure of Sodium Nitrite (NaNO₂)

Introduction

As mentioned above, isomerisms present in numerous molecules; even for a very small system like NaNO₂, linkage isomerism can occur. In this molecule, Nitrogen atom and Oxygen atoms can coordinate with the positively charged Na⁺ ion, which leads to two possible structures of the molecule. In this section, the structures would be optimised and their relative energies would be compared to predict the more stable structure.

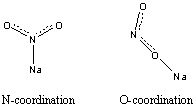Figure 19 - Ground State Theoretical Structures of NaNO2.

Optimisation

To compute the two structures, B3LYP method with 6-311G(d) basis set was used, which took into account all the electrons. Based on the first optimised results, different point group constraints were applied with tight toleration to determine the best optimised structure.

N-coordinated NaNO₂

Table 20 – Result Summary of NaNO2 Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00014256 Dipole Moment 9.8562 Debye Point Group CS Job Time 1 minute 33 seconds 3-D Structure

Table 21 – Result Summary of NaNO2 Optimisation with C1 Symmetry Constraint Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00014243 Dipole Moment 9.8562 Debye Point Group CS Job Time 32 seconds 3-D Structure

Table 22 – Result Summary of NaNO2 Optimisation with C2 Symmetry Constraint Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00013980 Dipole Moment 9.8563 Debye Point Group C2V Job Time 19 seconds 3-D Structure

Table 23 – Result Summary of NaNO2 Optimisation with C2V Symmetry Constraint Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00013980 Dipole Moment 9.8563 Debye Point Group C2V Job Time 19 seconds 3-D Structure

Based upon the 4 optimisation summaries, all 4 structures have very similar energies and dipole moments. Although N-coordinated NaNO₂ is not under a highly symmetrical point group, but it still has a certain level of symmetry; therefore by increasing its symmetry from C₁ to C_2V, the RMS gradient would decrease giving a better optimisation towards the stationary point of the potential energy curve. The bond lengths obtained from the optimisation are 1.24 Å for N-O bond and 2.20 Å for Na-N bond. The N-O bond length agrees with the literature value, 1.24 Å, hence this model is relatively accurate for the NO₂^- structure. Both C₁ and C₂ constraints did not work for the molecule, as they were being forced into C_S and C_2V respectively.

O-coordinated NaNO₂

The energies optimised are very similar but the RMS gradient shows that optimisation 6 is closer to the stationary point of potential energy curve of the structure, which is due to the tight toleration since the symmetry of the structure was being forced to be C_S. N-O bond length was computed to be 1.26 Å and Na-O bond length was optimised to be 2.22 Å; the N-O bond length agrees with the literature value as mention above, which is 1.24 Å.

Table 24 – Result Summary of NaONO Optimisation Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.53 Hatrees RMS Gradient Norm 0.00011119 Dipole Moment 7.3625 Debye Point Group CS Job Time 4 minute 1 seconds 3-D Structure

Table 25 – Result Summary of NaONO Optimisation with C1 Symmetry Constraint Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.53 Hatrees RMS Gradient Norm 0.00004528 Dipole Moment 7.3606 Debye Point Group CS Job Time 1 minute 20 seconds 3-D Structure

The log files for the optimisations can be accessed at

Optimisation 1:Media:NANO2_OPTIMISATION_chc08.LOG,	Optimisation 2:Media:NANO2_OPTIMISATION_C1_SYMMETRY_chc08.LOG,
Optimisation 3:Media:NANO2_OPTIMISATION_C2_SYMMETRY_chc08.LOG,	Optimisation 4:Media:NANO2_OPTIMISATION_C2V_SYMMETRY_chc08.LOG,
Optimisation 5:Media:NAONO_OPTIMISATION_chc08.LOG and	Optimisation 6:Media:NAONO_OPTIMISATION_C1_SYMMETRY_3_chc08.LOG

Vibrational Analysis

Vibrational frequencies are estimated to further determine which optimisation structure is the most optimised one; also, vibrational frequencies are used to confirm if the stationary point found by optimisation is the minima.

N-coordinated NaNO₂

Table 26 – Result Summary of Optimisation 1 Frequency Calculations. Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00014243 Dipole Moment 9.8562 Debye Point Group CS Job Time 1 minutes 47 seconds Low Frequency -172.0598 -10.9541 -4.8458 0.0013 0.0014 0.0018

Table 27 – Result Summary of Optimisation 2 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00014243 Dipole Moment 9.8562 Debye Point Group CS Job Time 1 minutes 35 seconds Low Frequency -172.0597 -10.9509 -4.8431 -0.0012 -0.0013 0.0015

Table 28 – Result Summary of Optimisation 3 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00013983 Dipole Moment 9.8563 Debye Point Group C2V Job Time 1 minutes 10 seconds Low Frequency -172.0556 -10.9202 -4.8854 -0.0005 -0.0004 0.0011

Table 29 – Result Summary of Optimisation 4 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.49 Hatrees RMS Gradient Norm 0.00013983 Dipole Moment 9.8563 Debye Point Group C2V Job Time 1 minutes 14 seconds Low Frequency -172.0556 -10.9202 -4.8854 -0.0005 -0.0004 0.0011

Although the low frequencies are not in the acceptable range, hence the method is not the best computational model for this structure, this can be explained by the very ionic nature of Na-N bond. For each optimised structure, there is one mode of vibration which has a negative frequency; this indicates all these structures are at a maximum stationary point, and so they are all transition state of the energy curve. Based upon optimisation results and vibrational frequencies, optimisation 4 is the best transition state structure.

O-coordinated NaNO₂

Table 30 – Result Summary of Optimisation 5 Frequency Calculations. Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.539 Hatrees RMS Gradient Norm 0.00011094 Dipole Moment 7.3625 Debye Point Group CS Job Time 1 minutes 45 seconds Low Frequency -8.3286 -7.3355 -0.0014 -0.0009 0.0005 12.0890

Table 31 – Result Summary of Optimisation 6 Frequency Calculations Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-311G(d) E(RB+HF-LYP) -367.53 Hatrees RMS Gradient Norm 0.00004519 Dipole Moment 7.3606 Debye Point Group CS Job Time 1 minutes 51 seconds Low Frequency -12.1952 -10.9119 -0.0015 0.0009 0.0011 6.5900

The low frequencies for both optimised structures are roughly in the acceptable range, therefore a better computational model should be used for this structure. All vibrational frequencies obtained are positive, which provide evidence these structures are at a minimum stationary point of the energy curve. Based upon optimisation results and vibrational frequencies, optimisation 5 is a better optimised structure.

The log files for the vibrational frequency calculations can be accessed at

Optimisation 1:Media:NANO2_FREQUENCY_chc08.LOG,	Optimisation 2:Media:NANO2_FREQUENCY_C1_SYMMETRY_chc08.LOG,
Optimisation 3:Media:NANO2_FREQUENCY_C2_SYMMETRY_chc08.LOG,	Optimisation 4:Media:NANO2_FREQUENCYC_C2V_SYMMETRY_chc08.LOG,
Optimisation 5:Media:NAONO_FREQUENCY_chc08.LOG and	Optimisation 6:Media:NAONO_FREQUENCY_C1_SYMMETRY_3_chc08.LOG

Conclusion

Theoretically based upon the two optimised structures, O-coordination would be predicted to be more stable as it has two oxygen atoms donating electron density towards the Na⁺, whereas N-coordination only has one coordination and the negative charge of the anion is delocalised among all three atoms making N less electron rich. The computational model estimate the N-coordination is the transition state whilst the O-coordination is the ground state, this suggests that when the anion is rotating, it would rotate from the O-coordination state to the N-coordination state, and then return to O-coordination state. The method used for the project is B3LYP, which is a low level calculation method; to improve the results, a higher level method can be applied, but it would increase the time consumption. For such ionic compound, molecular orbital may not be the best approach to analyse stability as it depends more on the Coulombic interactions between the opposite charged species than the orbital overlap.