Module One: Structure and Spectroscopy (Molecular Mechanics / Molecular Orbital Theory)

Introduction

Molecular structure and its spectroscopic characteristics can now be modelled accurately, which gives an insight about reactivity and selectivity of a molecule before conducting an experiment. Structural optimisation is often based on theories such as steric hindrance, inter/intra-molecular interactions, stereoelectronic interactions, while quantum mechanical approximation is used to estimate molecular orbitals and spectroscopic information.

Modelling using Molecular Mechanics

Molecular Mechanics

The Molecular Mechanics(MM) approach is based upon force field mechanics, hence a non-quantum mechanics method. The steric energy of a molecule is defined by the following five parameters:

Bond stretches
Bond angles
Dihedral angles
Intermolecular forces, including both Van der Waals repulsion forces and dipolar electrostatic attraction forces
Hydrogen bonds, which usually is a zero term

$E_{s t e r i c} = \sum_{b o n d s} K_{r} (r - r_{e q})^{2} + \sum_{a n g l e s} K_{θ} (θ - θ_{e q})^{2} + \sum_{d i h e d r a l s} \frac{V_{n}}{2} [1 + c o s (n ϕ - γ)] + \sum_{n o n - b o n d e d} [\frac{A_{i j}}{R_{i j}^{12}} - \frac{B_{i j}}{R_{i j}^{6}} + \frac{q_{i} q_{j}}{ϵ R_{i j}}] + \sum_{H - b o n d e d} [\frac{C_{i j}}{R_{i j}^{12}} - \frac{D_{i j}}{R_{i j}^{10}}]$ Equation 1 - Force Field Mechanics Equation on calculating Steric Energy of a Molecule

The first three terms of Equation 1 are related to the strain effects, and are minimised to zero when the molecule is unstrained and unhindered. The non-bonded term can take on negative values, particularly if there are numerous inter/intra-molecular attractive terms or favourable ionic interactions. The Hydrogen bond term is considered as just between two specific atoms, thus no de-localised Hydrogen bonds are covered. π-conjugation and stereo-electronic (anomeric) effects are often being taken into account by the addition of two more terms in the sum. The main assumption of force field mechanics is the five parameters do not have any interactions among them, hence it would start to break down when unusual bondings are involved. The two models that are being used to find the closest low energy conformation during this module are MM2 and MMFF94, as different models based on different force field formulae, thus the energies calculated can only be compared with similar molecules such as isomers and conformers, also energies calculated from different models cannot be compared.

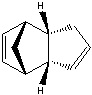
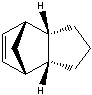
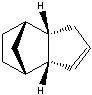
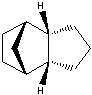
The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadine undergoes dimerisation at room temperature, the dimer has two possible conformations, exo- and endo-dimer.
The reaction is a Diels-Alder reaction, which is a typical example of pericyclic reaction. It can only happen when the cyclopentadienes have the right orientation to allow orbitals overlap, the HOMO and LUMO from the diene and dienophile.

The energies of the two possible conformers were calculated via MM2 and the results are presented in Table 1.

Based on the calculations, exo-dimer is at a lower energy level than endo-dimer, but experimentally endo-dimer is major, in fact the only product. This shows that the reactions is kinetically governed rather than thermodynamically controlled. This can be explained by the energies of the respective transition states, as endo-dimer has lower activation energy (refer to Figure 2).

*Table 1 – MM2 calculated energies of exo-dimer and endo-dimer*
	Exo-dimer	Endo-dimer
Structure
3-D Structure
Total Energy	31.88 kcal/mol	34.00 kcal/mol
Stretch Energy	20.56 kcal/mol	20.84 kcal/mol
Bend Energy	20.56 kcal/mol	20.84 kcal/mol
Stretch-Bend Energy	-0.83 kcal/mol	-0.83 kcal/mol
Torsion Energy	7.66 kcal/mol	9.51 kcal/mol
Non-1,4 Van der Waals Energy	-1.40 kcal/mol	-1.56 kcal/mol
1,4 Van der Waals Energy	4.24 kcal/mol	4.33 kcal/mol
Dipole-dipole Interaction Energy	0.38 kcal/mol	0.45 kcal/mol

The endo-dimer has a more favourable transition state due to more favourable orbital overlap in comparison with exo-dimer's transition state.
Hydrogenation can be carried out to reduce the C=C bonds of cyclopentadiene dimer; specific conditions can be introduced to gain selectivity control between the two C=C bonds. MM2 was used to calculate the energies of the three possible products and the results are illustrated in Table 2.

*Table 2 – MM2 calculated energies of product 1,2 and 3*
	Product 1	Product 2	Product 3
Structure
3-D Structure
Total Energy	35.93 kcal/mol	31.16 kcal/mol	35.28 kcal/mol
Stretch Energy	1.23 kcal/mol	1.10 kcal/mol	1.12 kcal/mol
Bend Energy	18.86 kcal/mol	14.52 kcal/mol	12.98 kcal/mol
Stretch-Bend Energy	-0.76 kcal/mol	-0.55 kcal/mol	-0.48 kcal/mol
Torsion Energy	12.22 kcal/mol	12.51 kcal/mol	16.91 kcal/mol
Non-1,4 Van der Waals Energy	-1.52 kcal/mol	-1.06 kcal/mol	-1.34 kcal/mol
1,4 Van der Waals Energy	5.74 kcal/mol	4.51 kcal/mol	6.10 kcal/mol
Dipole-dipole Interaction Energy	0.16 kcal/mol	0.14 kcal/mol	-

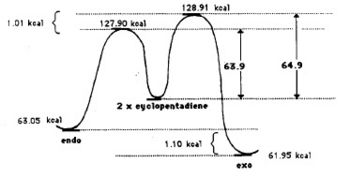Product 1 and 2 are results of hydrogenation of one C=C bond of the endo-dimer, whereas product 3 is the result of both C=C bonds being reduced. The energy of product 2 is lower than product 1, which suggests formation of product 2 is thermodynamically more favourable. Both product 1 and 2 can undergo further hydrogenation to give product 3, but the reaction would not be thermodynamically favourable; this can be explained by the similar energies of product 1 and 2 and the energy of product 3 is higher than product 2. To make the reaction happens, nickel(II) chloride with water can be used to catalyse it, and the first C=C bond being reduced is the one as product 2 which agrees with the calculation ^[2]. Based upon the calculations, the key energy that distinguish between product 1 and 2 is bend energy. Product 1 has higher bend energy (~4 kcal/mol) than product 2, which mainly causes the destabilisation of product 1. Although product 3 has the lowest bend energy among the three, but it has the highest torsion energy and therefore causes destabilisation of the molecule.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ Analogue)

The two reactions below demonstrate nuclephilic additions to pyridinium rings, both products have specific stereochemistry and this can be predicted based on the geometry optimised structures.

The first reaction is the addition of a methyl group to a pyridinium ring via a Grignard reagent as shown in Figure 3. By performing MM2 minimisation, the lowest energy conformation of compound 4 is of 42.75 kcal/mol. The conformation of oxygen atom pointing below the plan is of higher energy, thus reaction would go via the conformation as shown below. They key stage of the reaction, which determines the stereochemistry of the product, is when Magnesium atom coordinated with the oxygen before performing the nucleophilic attack as shown in Figure 4. The 6 member ring transition state of the reaction results in the attack of from the same side, hence yielding one stereochemically pure product. The dihedral angles calculated for the carbonyl group with respect to the pyridinium ring were 24^o and 10^o, which further support the favourable way of attack.

*Table 3 – Geometry Optimised Structures of Compound 4 and Product 5 by MM2*
	Compound 4	Product 5
3-D Structure
Total Energy	42.75 kcal/mol	37.41 kcal/mol

Figure 3 - Reaction Scheme for the Formation of Product 5.

Figure 4 - Reaction Mechanism of Product 5 Formation.

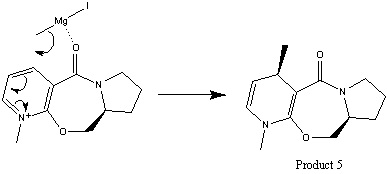
The second reaction is nucleophilic addition of NHPh group to pyridinium ring, unlike the above reaction, the oxygen does not coordinate with the nucleophile. The lowest energy conformation obtained by MM2 is with oxygen at the lower plane and therefore increases the steric hindrance of the lower plane. The attack of the nucleophile is at the upper plane so the steric effects can be minimised due to the bulky phenyl group of the nucleophile giving a stereochemically pure product.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

The synthesis of taxol involves an intermediate which demonstrates atropisomerism; compound 8 and 9 differ in the conformation of C=O bond, whether it is pointing up or down. Both compounds were minimised by MM2, the results show that compound 9 is more stable than compound 8, thus during the reaction compound 8 would convert to compound 9 to give a more stable intermediate can be expected. The major difference between the two compounds is their relative torsion energy due to the rotation of C=O bond. MMFF94 approach agrees with MM2, but since two methods have different combination of force field, hence the energies calculated are different.

*Table 4 – Calculated Energies of Compound 8 and 9*
	Compound 8	Compound 9
Structure
3-D Structure
MM2 Calculated Total Energy	48.89 kcal/mol	44.35 kcal/mol
MMFF94 Calculated Total Energy	70.54 kcal/mol	60.56 kcal/mol

The alkane product of the intermediate is at a higher energy level (68.37 kcal/mol as estimated by MM2), this suggests that the C=C bond causes stabilisation of the compound. This is known as hyperstable alkene^[3], which would occur when C=C bond adjacent to a bridgehead, hence the structure suffers less strain.

Modelling Using Semi-empirical Molecular Orbital Theory

MM approach is useful when optimising geometries of molecules and calculating their relative energies. As it is a non-quantum mechanics method, it cannot compute electrons, hence orbital interactions. Semi-empirical molecular orbital(MO) theory is introduced to take into account electron interactions, hence a quantum mechanics approach.

Regioselective Addition of Dichlorocarbene

Compound 10 was chosen to study the regioselectivity of dichlorocarbene addition, as there are two possible sites to perform the addition as shown in Figure 6.

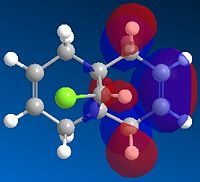
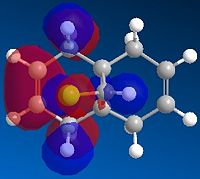
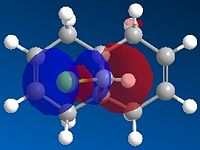
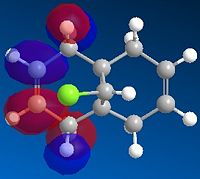
The geometry of the compound was minimised by MM2 to give a total energy of 17.00 kcal/mol. MOPAC/RM1 MO method was performed to generate the molecular orbitals of the structure, which can be used to distinguish between the two C=C bonds. The key molecular orbitals are shown in Table 5.

*Table 5 – Molecular Orbitals Generated by MOPAC/RM1 MO method*
HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

These molecular orbitals demonstrate an anti-periplanar stabilising overlap of the syn π orbital in the HOMO-1 and the empty σ* C-Cl of the LUMO +1, which lowers the energy of the syn C=C bond relative to the anti C=C bond. This results in syn C=C bond as a poorer electron acceptor, thus product 13 would be formed due to both stereoelectronic effects and steric effects.
Besides molecular orbital analysis, vibrational stretching can also be used to identify the site of addition. The infra-red spectrum of Compound 12 was calculated by Gaussian and the key peaks were reported in Table 6.

*Table 6 – Key infra-red spectrum peaks of Compound 12 and 15*
	Compound 12		Compound 15
3-D Structure
	Wavenumber (cm^-1)	Vibration Image	Wavenumber (cm^-1)	Viration Image
C-Cl Stretch	770.86		780.03
syn-periplanar C=C stretch	1757.34		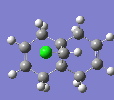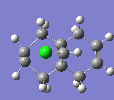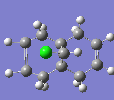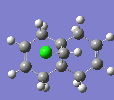1753.72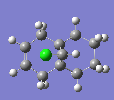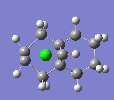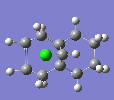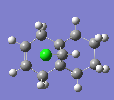
anti-periplanar C=C stretch	1737.03		-

The vibrational frequency of syn C=C bond is higher than that of anti C=C bond, which indicates anti C=C bond is weaker and is easier to break, hence it is more likely to be attacked by nucleophiles.

Compound 15 is the anti C=C hydrogenated product of Compound 12. The C-Cl stretch of Compound 12 is at a lower vibrational frequency hence the bond is weaker than that it would be in Compound 15. This can be explained by the secondary orbital overlap, anti C=C π bond donates electron density into the σ* C-Cl anti-bonding orbital and increases anti-bonding character in the C-Cl bond.

Figure 9 - Reaction Scheme for Compound 15.

Structure Based Mini Project^[4] Using DFT-based Molecular Orbital Methods

Mini Project Introduction

Carbon-carbon bond forming reactions are crucial in organic synthesis and polymer chemistry, especially ring closing metathesis reaction, which plays an essential role. It is a powerful tool in synthesising macro-cyclic system, such as the key step in synthesising BILN 2061 ZW, which is a chemical entity showing promising results against the Hepatitis C virus.

The specific reaction chosen for this project is shown in Figure 11. The reaction conditions would give 84% as experimental yield and the mole ratio of cis- to trans-product is 2:3. The diaselectivity of the reaction is the result of the steric effects cause by the ligands around Ru atom.

Conformational Analysis

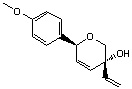
MM2 was performed to obtain the conformations with the minimum total energies for both cis- and trans- product. The results are shown in Table 7.

*Table 7 –MM2 calculated energies of cis- and trans-product 25*
	Cis-product 25	Trans-product 25
Structure
3-D Structure
Total Energy	13.51 kcal/mol	14.31 kcal/mol
Stretch Energy	1.11 kcal/mol	1.11 kcal/mol
Bend Energy	4.62 kcal/mol	4.44 kcal/mol
Stretch-Bend Energy	0.20 kcal/mol	0.22 kcal/mol
Torsion Energy	-3.06 kcal/mol	-2.92 kcal/mol
Non-1,4 Van der Waals Energy	-5.34 kcal/mol	-3.89 kcal/mol
1,4 Van der Waals Energy	14.90 kcal/mol	13.82 kcal/mol
Dipole-dipole Interaction Energy	1.08 kcal/mol	1.53 kcal/mol

MM2 calculations show that cis-product is of a lower energy (~ 1 kcal/mol) than trans-product,hence thermodynamically more stable due to the stabilisation by torsion energy, non-1,4 Van der Waals energy and dipole-dipole interaction energy. The synthetic experiment shows that trans-product has a higher mole ratio in the product mixture, this suggests that the reaction is kinetically governed, thus formation of trans-product goes via a more stable transition state with smaller activation energy barrier.

¹³C NMR Spectrum Estimation

After minising the structures by MOPAC/RM 1 MO method, the data were processed by Gaussian to give the ¹³C NMR estimations.

*Table 8 –Calculated ¹³C NMR Data for Cis-product 25*
Chemical Shift (ppm)	Literature Chemical Shift (ppm)	Deviation	Carbon Environment
154.2	159.6	5.4	C11
140.0	138.7	1.3	C2
131.6	131.9	0.3	C5
128.1	131.8	3.7	C4
127.9	130.1	2.2	C8
126.6	128.7	2.1	C13
114.7	115.8	1.1	C1
113.4	114.0	0.6	C12
107.1	-	-	C10
77.9	76.4	1.5	C6
75.7	74.2	1.5	C7
69.1	68.0	1.1	C3
53.0	55.3	2.3	C14

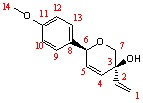Based upon Table 8, the Carbon-10 is not observed in the experimental NMR data since it is in the same environment as Carbon-12, hence one peak with double intensity would be shown. The same principle applies to Carbon-9 and -13.

*Table 9 –Calculated ¹³C NMR Data for Trans-product 25*
Chemical Shift (ppm)	Literature Chemical Shift (ppm)	Deviation	Carbon Environment
153.2	159.5	6.3	C11
141.6	140.1	1.5	C2
129.9	131.4	1.5	C5
129.3	130.3	1.0	C8
127.8	129.2	1.4	C4
124.2	127.9	3.7	C13
124.0	-	-	C9
113.3	115.0	1.7	C1
108.8	113.9	5.1	C10
106.8	-	-	C12
77.6	75.1	2.5	C6
73.0	71.4	1.6	C7
69.4	68.5	0.9	C3
52.9	55.3	2.3	C14

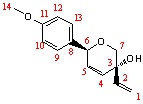In comparison with the literature of Trans-product, Carbon-9 and -12 should be merged with Carbon-13 and-10 respectively due to two identical Carbon environments; this can explain the relatively large deviations for those peaks.
The key peak in identifying the two isomers is Carbon-7 as in the literature they have the largest difference comparing with relative Carbon environment; this effect is arisen by the chiral centre (Carbon-3).

Conclusion

Based upon the results obtained ¹³C NMR is not the best method in identifying the two products, as most peaks are very similar. Alternatively ¹H NMR would be a better spectroscopic approach, as the chemical shifts and coupling constants are different between the two products.

Reference

↑ M. A. Fox, R. Cardona and N. J. Kiwiet, Journals of Organic Chemistry, 1987,52, 1469-1474
↑ F. Alonso and M. Yus, Tetrahedron Letters, 1996, 37, 6925-6928
↑ W. Maier and P. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1893
↑ B. Schmidt and M. Westhus, Tetrahedron, 2000, 56, 2421-2426
↑ T. Nicola, M. Brenner, K. Donsbach and P. Kreye, Organic Process Research & Development, 2005, 9, 513-515

[1] M. A. Fox, R. Cardona and N. J. Kiwiet, Journals of Organic Chemistry, 1987,52, 1469-1474

[2] F. Alonso and M. Yus, Tetrahedron Letters, 1996, 37, 6925-6928

[3] W. Maier and P. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1893

[4] B. Schmidt and M. Westhus, Tetrahedron, 2000, 56, 2421-2426

[5] T. Nicola, M. Brenner, K. Donsbach and P. Kreye, Organic Process Research & Development, 2005, 9, 513-515

[1]

[2]

[3]

[4]

[5]