Rep:Mod:cg507
Module 1: Structure and Spectroscopy
The Hydrogenation of Cyclopentadiene Dimer
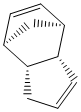
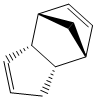
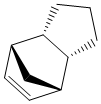
Cyclopentadiene dimerises to produce two products, an exo product (1) and an endo product (2), which is the favoured dimer. Hydrogenation of the dimer initially provides one of the dihydro derivatives (3) or (4) before proceeding to the tetrahydro derivative after prolonged hydrogenation.
 |
 |
 |
 |
To investigate the energies of the different dimers and their dihydro derivatives they were defined using ChemBio3D Ultra and their geometries were optimised using the MM2 force field. The energies calculated using this force field for products 1-4 are presented in table 1. The dimerisation and the hydrogenation products are dictated by thermodynamic and kinetic controls. A kinetic product will be obtained if the product is obtained via the transition state with the lowest energy, and hence has a lower energy activation barrier. A thermodynamic product will be the product with the lowest energy.
The thermodynamically most stable dimer is the one with the lowest total energy, which, as it can be seen from table 1 is the exo dimer. This suggests that the preferred endo dimer is formed under kinetic control, with the lowest energy activation barrier, and hence is the kinetic product of the dimerisation.


| Energy (kcal/mol) | ||||
|---|---|---|---|---|
| Structure | Exo Product - 1 | Endo Product - 2 | Product 3 | Product 4 |
| Stretch | 1.29 | 1.24 | 1.24 | 1.10 |
| Bend | 20.58 | 20.87 | 18.97 | 14.51 |
| Stretch-Bend | -0.84 | -0.84 | -0.76 | -0.55 |
| Torsion | 7.66 | 9.51 | 12.15 | 12.50 |
| Non-1,4 VDW | -1.42 | -1.05 | -1.56 | -1.05 |
| 1,4 VDW | 4.23 | 4.33 | 5.73 | 4.51 |
| Dipole/Dipole | 0.38 | 0.45 | 0.16 | 0.14 |
| Total Energy | 31.88 | 34.00 | 35.93 | 31.15 |
The thermodynamic product of the hydrogenation of the dimer is product 4. This is the product with the lowest total energy , see table 1. The hydrogenation of the dimer is a thermodynamically controlled reaction and product 4, the energetically most stable dihydro derivative will be preferred product before any further hydrogenation occurs.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Prolinol Derivative - Reactant 5
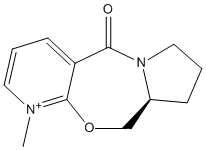

Reactant 5 is an optically active derivative of prolinol which will react with MeMgI to alkylate the pyridinium ring at the 4- position with a precise resulting stereochemistry. To find out more about the why the reaction is so stereospecific energy minimisations were performed to provide a geometry of 5 which had the lowest energy. As these minimisations could adopt different structures according to which minima the energy minimisation found, I distorted the starting conformation of the reactant to see a clearer picture of what the most common conformation of the reactant is. I decided to measure and change the distortion of reactant 5 by moving the carbonyl and measuring the dihedral angle between the carbonyl and and the pyridinium ring. As it can be seen from table 2, the carbonyl could occupy a position on either side of the ring. However the energies of the the conformations were significantly different depending on which side of the ring the carbonyl occupied. This would mean that the reactant would would, for most of the time have a set confirmation, with a significantly lower energy. This provides a sterically less hindered side of the pyridinium ring that will more easily be attacked, providing a stereospecific reaction.
| Energy (kcal/mol) | |||||
|---|---|---|---|---|---|
| Dihedral Angle | -11.5757 | 23.2238 | -167.9957 | 23.2183 | |
| Stretch | 18.9807 | 1.3188 | 4.3758 | 1.3314 | |
| Bend | 201.6287 | 8.2523 | 80.8810 | 8.3295 | |
| Stretch-Bend | -4.4883 | 0.1226 | -0.9647 | 0.1298 | |
| Torsion | 29.2869 | 13.6598 | 25.8967 | 13.5507 | |
| Non-1,4 VDW | 5.0198 | -1.6263 | -1.0849 | -1.6222 | |
| 1,4 VDW | 42.3833 | 15.9977 | 23.1861 | 16.0161 | |
| Charge/Dipole | 10.2440 | 10.2564 | 11.6543 | 10.2487 | |
| Dipole/Dipole | -1.9133 | -3.8732 | -2.6146 | -3.8791 | |
| Total Energy | 301.1419 | 44.1076 | 141.3297 | 44.1048 | |
Reactant 7
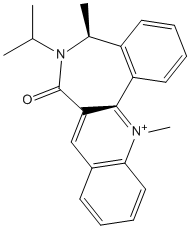

Reactant 7 also undergoes highly stereospecific reactions, here we again investigated this using by trying to change the dihedral angle between the carbonyl and the pyridinium ring. As it can be seen from table 3, although this angle could be changed slightly, a significantly different conformation could not be obtained. As the carbonyl was moved into different postions the energy minimisation would always return the molecule to a similar conformation. This shows us that this molecule will always prefer the carbonyl group to lie on one side of this ring. Hence when there is an attack on the pyridinium ring it will always have to happen on one face of the ring, providing a highly stereospecific reaction.
| Energy (kcal/mol) | |||||
|---|---|---|---|---|---|
| Dihedral Angle | 21.1127 | 23.5679 | 24.7108 | 26.9055 | 28.0706 |
| Stretch | 5.8939 | 5.9220 | 6.1013 | 6.0385 | 6.3251 |
| Bend | 17.6865 | 17.8762 | 18.5854 | 18.6274 | 20.0254 |
| Stretch-Bend | 0.5100 | 0.5096 | 0.5396 | 0.5487 | 0.6052 |
| Torsion | 20.4903 | 20.5261 | 18.7155 | 18.9399 | 15.8426 |
| Non-1,4 VDW | 6.6915 | 6.4245 | 6.9416 | 6.7346 | 7.7488 |
| 1,4 VDW | 29.5476 | 29.5794 | 29.7093 | 29.6761 | 29.9044 |
| Charge/Dipole | 9.4841 | 9.4150 | 9.3882 | 9.3943 | 9.4048 |
| Dipole/Dipole | -4.9121 | -4.9076 | -4.9183 | -4.9170 | -4.9225 |
| Total Energy | 85.3451 | 85.3451 | 85.0625 | 85.0425 | 85.9298 |
Stereochemistry and Reactivity of an Intermediate In the Synthesis of Taxol
 |
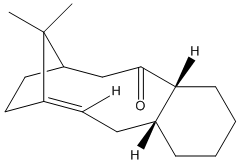 |
Taxol is an important drug used in the treatment of cancers, a key intermediate in the synthesis of this drug is 9 or 10. The inermediates is formed with the carbonyl group pointing up (9) or down (10), which readily interconvert. This is an example of atropisomerism and the stereochemistry of the carbonyl addition depends on the stability of these intermediates. When an energy and geometry minimisation is applied to 10, during the minimisation the conformation of the intermediate reverts from (10) to (9). This provides a higher energy than the energy for 10 actually is. When altering the structure to obtain an energy minimisation for the intermediate 10, another intermediate, where the carbonyl group is equatorial was found. Although it took some manipulation of the the structure to find the energies of the intermediate 10 it was found that this intermediate is the thermodynamically most stable. The intermediate 10 has its hexane ring in a chair conformation, a more stable conformation than the higher energy hexane conformation present in the intermediate of 9. The conformation adopted will depend on how the carbonyl addition occurs and the shape that the addition forces the hexane ring to adopt.
 |
 |
| Energy (kcal/mol) | ||||
|---|---|---|---|---|
| Structure | Intermediate 9 | Intermediate 10 | Equatorial Intermediate | |
| Stretch | 2.8196 | 2.5558 | 4.4793 | |
| Bend | 16.4243 | 10.7721 | 76.7004 | |
| Stretch-Bend | 0.4544 | 0.3193 | -0.0297 | |
| Torsion | 21.3846 | 19.7453 | 19.9728 | |
| Non-1,4 VDW | -0.8660 | -1.4578 | -1.3988 | |
| 1,4 VDW | 14.0299 | 12.5515 | 25.0372 | |
| Dipole/Dipole | 0.1375 | -0.1804 | -0.0918 | |
| Total Energy | 54.3843 | 44.3057 | 124.6693 | |
| Total Energy MMFF94 force field | 76.3086 | 60.5578 | 81.5568 | |
It has also been observed previously that during the functionalisation of alkene it reacted abnormally slowly. This is because of a the stability of the bridgehead alkene induced by the conformation of the attached ring structure, for further information on the stability of these 'hyperstable' bridgehead alkenes see the article on the 'Evaluation and prediction of the Stability of Bridgehead Olefins[1].
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
The orbital control of a reaction can be very important, and hence a detailed understanding of of obitals and the geometry of the orbitals or a reactant is very important. Here we will be looking at a classical mechanics and a quantum mechanical treatment, including a wave-description of electrons, to analyse the geometry of the molecule.
First we performed a MM2 energy minimisation of the molecule, the results of which can be seen in table 5. We then used performed a MOPAC interface minimisation using the PM6 method, this provides an approximate representation of the valence-electron molecular wavefunction. The highest occupied molecular orbital (HOMO) and the lowest occupies molecular orbital (LUMO) and and orbitals nearest in energy to these are presented as they are the most important molecular orbitals involved in in a reaction. The HOMO is the molecular orbital which is most susceptible to electrophilic attack and the LUMO is most susceptible to the attack of a nucleophile.
| Energy Contribution | Energy (kcal/mol) |
|---|---|
| Stretch | 0.6260 |
| Bend | 4.7787 |
| Stretch-Bend | 0.0399 |
| Torsion | 7.6311 |
| Non-1,4 VDW | -1.0781 |
| 1,4 VDW | 5.7879 |
| Dipole/Dipole | 0.1119 |
| Total Energy | 17.8975 |
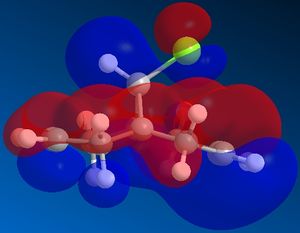
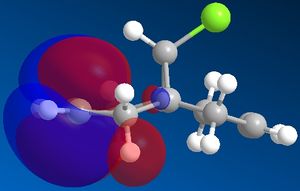
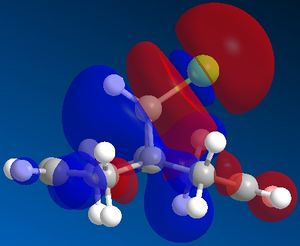
Molecular orbitals of molecule 12:
 |
 |
 |
 |
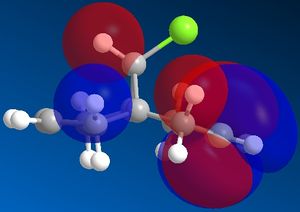 |
The molecular orbitals show us the large difference in the electron density distributions beteen the the occupied lower energy bonding orbitals (HOMO and HOMO-1) and the higher energy non-occupied orbitals (LUMO, LUMO+1 and LUMO+2). In the first non occupied orbital, the LUMO orbital, the molecular orbitals are located around the C=C double bond anti in position to the C-Cl bond. This means that an nucleophilic addition to this molecule would be most likely to occur here at this alkene. The alkene on the same side of the molecule to the Cl has a higher density of bonding molecular orbitals in the HOMO, which means that there is a higher electron density present at this alkene, making it most susceptible to electrophilic attack and hence the most nucleophilic alkene in the molecule.
In the next part of this investigation the C=C double bond anti (or exo) in position to the C-Cl bond was replaced with a single C-C bond. The purpose of this part of the investigation is to observe the influence of the C-Cl bond on the vibrational frequencies of the molecule. The most reliable way to calculate the vibrational frequencies is to use a density functional approach, this involves subjecting molecule 12 and its dihydro derivative 13 to B3LPY/6-31G9(d,p) Gaussian geometry optimisation and frequency calculation. These calculations have a greater computational cost than than the previous calculations we have performed and these are performed using the high performance computer which runs multiple processors in parallel to speed up the time taken to perform the calculations.
The affect of the C-Cl bond on the vibrational frequencies of molecules 12 and 13 can be seen in table 7. The C=C double bond has a higher vibrational frequency in the syn position than it does in the exo (anti) position. This supports the conclusions from before as the syn double bond is higer in vibrational energy due to the localisation of electrons in what is the highest occupied molecular orbital. The high vibrational energy makes this double bond weaker and more susceptible to electrophilic attack. It can also be seen that the hydrogenation of the C=C double bond appears to increase the vibrational energy of the syn C=C bond and the C-Cl bond. This observation is supported in the molecular orbital representations as the orbitals involved in this double bond are higher in energy and the occupation of these molecular orbitals would raise the energy of the molecule slightly.
| Energy Contribution | Energy (kcal/mol) |
|---|---|
| Stretch | 0.8968 |
| Bend | 4.7287 |
| Stretch-Bend | 0.0170 |
| Torsion | 10.7244 |
| Non-1,4 VDW | -1.0138 |
| 1,4 VDW | 6.9292 |
| Dipole/Dipole | 0.0710 |
| Total Energy | 22.3533 |
 |
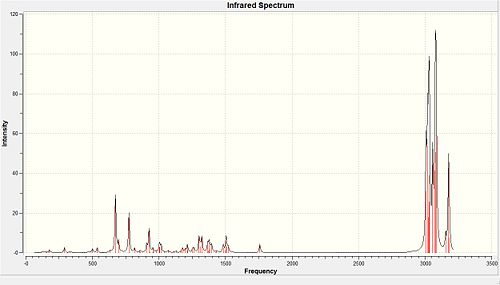 |
| Bond Stretch | Vibration (Hz) | |||
|---|---|---|---|---|
| Structure | 12 | 13 | ||
| anti C=C | 1737.03 | N/A | ||
| syn C=C | 1757.44 | 1758.06 | ||
| C-Cl | 770.81 | 774.97 | ||
Structure based Mini project using DFT- based Molecular orbital methods
A significant number of synthetic reactions can give a mixture of products, depending on the position of attack, type of attack and which functionalised part of the molecule is attacked. This produces a mixture of many different isomers, it is very important to be able to separate and identify the different isomers, and be able to predict which isomer would be preferentially formed and why it is more stable. Understanding the mechanism of a reaction can help to predict these things, however these predictions need to be confirmed. Computational chemistry provides a route to predict many different properties of various isomers and there conformations which can be used to compare with experimental techniques. The techniques that can be predicted include; the spin-spin decoupled spectrum, infra-red spectra, optical rotations and the circular dichroism spectrum. All of these tecniques can be predicted with reasonable accuracy.
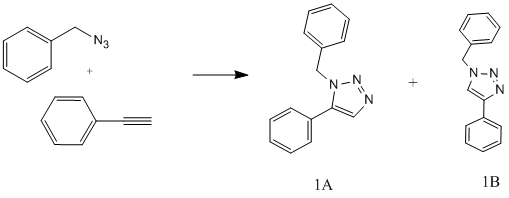
The 1,3-dipolar cycloaddition of an azide to an alkyne to form a 1,2,3-triazole, has been recognised for a long time however the reactions have a high activation energy (24-26kcal/mol)[2] and hence are slow even at high temperatures producing a mixture of regioisomers. However more recently a copper catalysed reaction has been discovered that is easily implemented, greatly speeds up the reaction providing specifically the 1,4-disubstituted product. It is often named the 'click reaction' an example of 'click chemistry' which was introduced by K. Sharpless. This field aims to use reactions that quickley and reliable join small units together. The high selectivity of the cycloaddition has meant that this reaction has become very important in many areas including protein labelling.
Here we investigate the stereoselective 1,5 disubstituted product using a ruthenium catalysed 'fusion' of organic azides with alkynes, as investigated by Li Zhang, Xinguo Chen, Peng Xue, Herman H. Y. Sun, Ian D. Williams, K. Barry Sharpless, Valery V. Fokin, and Guochen Jia. In the paper 'Ruthenium-Catalyzed Cycloaddition of Alkynes and Organic Azides'[2].
The preference between the 1,4-disubstituted and the 1,5-disubstituted can be altered by altering the catalyst. In the presence of Ru(OAc)2(PPh3)2 the 1,4-disubstituted (1B) product is obtained and using Cp*RuCl(PPh3)2 the 1,5-disubstituted (1A) product is formed.
To investigate this using the computational approach first an initial refinement of the geometry and the energy minimised was performed using the MM2 force field, table 8. We then used performed a MOPAC interface minimisation using the PM6 method, this provides an approximate representation of the valence-electron molecular wavefunction.
| Energy (kcal/mol) | ||||
|---|---|---|---|---|
| Structure | Regioisomer A | Regioisomer B | ||
| Stretch | 1.1119 | 0.8055 | ||
| Bend | 18.0895 | 13.2114 | ||
| Stretch-Bend | 0.1079 | -0.0167 | ||
| Torsion | -15.3357 | -14.7410 | ||
| Non-1,4 VDW | 0.6865 | -1.4294 | ||
| 1,4 VDW | 14.3621 | 14.7899 | ||
| Dipole/Dipole | -1.6697 | -1.4381 | ||
| Total Energy | 17.3525 | 11.1816 | ||
Table 8 shows that 1B, the 1,4-disubstituted product is the thermodynamically most stable product. Depending on what the catalyst used a the reaction barrier to products is lowered by providing an alternative reaction route, this can lead to the product 1A or 1B depending on the route taken and the energies involved. The initial geometry was then optimised using a DFT=mpw1pw91 method using a 6-31G(d,p) basis set and run on the high performance computer. Using the optimised geometry various calculations were performed; NMR chemical shift calculation, infra-red spectrum of the compound and the optical rotation, the data is presented below.
 |
 |
Data provided from the original article:
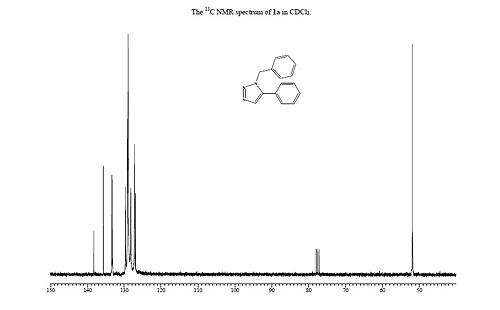
13C NMR (CDCl3): δ 51.85, 126.93, 127.22, 128.22, 128.92, 129.08, 129.64, 133.26, 133.34, 135.66, 138.26.
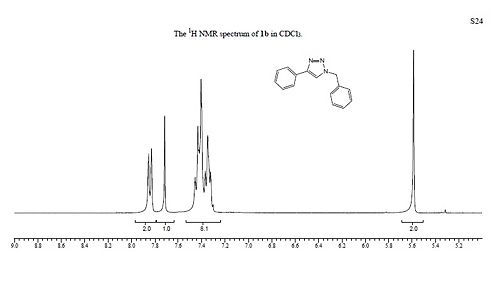
The experimental data matches the calculated data relatively well, with the same general pattern of the NMR chemical shifts emerging for the different isomers. Although the chemical shifts reported are shifted slightly from the experimental values, which could suggest that the optimisation doesn't find the exact geometry, it could could also be due to errors I have made in the calculation process. Although the chemical shifts for 1B were not reported in the original article, by comparison of the provided plots the general trend can be seen to agree with the calculated data. What the calculations do show is that it would be experimentally easy to differentiate between the two products as their NMR chemical shifts, infra-red spectra and the optical density are all noticeably different for each product.
| Carbon | Chemical Shifts (ppm) | ||||
|---|---|---|---|---|---|
| 18 | 57.42 | ||||
| 23 | 125.9 | ||||
| 24 | 125.94 | ||||
| 25 | 126.93 | ||||
| 5 | 126.94 | ||||
| 1 | 127.04 | ||||
| 4 | 127.08 | ||||
| 3 | 127.11 | ||||
| 26 | 127.27 | ||||
| 22 | 127.34 | ||||
| 2 | 137.58 | ||||
| 6 | 129.39 | ||||
| 21 | 133.09 | ||||
| 8 | 137.78 | ||||
| Carbon | Chemical Shifts (ppm) | ||||
|---|---|---|---|---|---|
| 6 | 57.87 | ||||
| 14 | 122.79 | ||||
| 16 | 125.56 | ||||
| 10 | 126.27 | ||||
| 8 | 126.43 | ||||
| 12 | 126.56 | ||||
| 15 | 126.76 | ||||
| 9 | 126.88 | ||||
| 1 | 127.05 | ||||
| 13 | 128.26 | ||||
| 10 | 134.59 | ||||
| 7 | 154.40 | ||||
| 2 | 133.09 | ||||
 |
 |
 |
 |
 |
 |
| Optical Rotation (degrees) | ||||
|---|---|---|---|---|
| Structure | 1A | 1B | ||
| 232.71 | 146.99 | |||
Key Literature and Data
Maier, W.F., Von Rague Schleyer, P., 1981, 'Evaluation and prediction of the stability of bridgehead olefin' J. A. Chem. Soc., 103 (8), 1891-1900 DOI: [1]
Zhang, L. et al, 2005 'Ruthenium-Catalyzed Cycloaddition of Alkynes and Organic Azides', J. American Chemical Soc. 127(46), 15998-15999 DOI: [2]
Data from the analysis of 1A and 1B:
1A NMR Data, http://hdl.handle.net/10042/to-6506
1B NMR Data, http://hdl.handle.net/10042/to-6507
1A IR Data, http://hdl.handle.net/10042/to-6524
1B IR Data, http://hdl.handle.net/10042/to-6523
1A OR Data, http://hdl.handle.net/10042/to-6525
1B OR Data, http://hdl.handle.net/10042/to-6526