Rep:Mod:cfl083

Module 3: Charlene Lawton

The Cope Rearrangement of 1,5-hexadiene

The low-energy minima and transition states on the potential energy surface (PES) of 1,5-hexadiene were investigated to determine the preferred reaction mechanism. The [3,3]-sigmatropic shift rearrangement (shown below) occurs in a concerted fashion passing through a chair or boat transition state (TS).

The Cope Rearrangement and TS of 1,5-hexadiene

Optimizing the Reactants and Products

The geometry of 1,5-hexadiene in an anti-periplanar (APP) arrangement and in a gauche arrangement were optimised at the HF/3-21G level of theory. This gave the results tabulated below.

Optimised Gauche and APP 1,5-hexadiene conformers

Point Group	C2	C1
Energy/ Hartree	-231.69260	-231.69266

It was expected that the gauche linkage would be less stable than the anti linkage; however the computed energies above show the gauche model to be more stable which is in agreement with literature . This is because the additional H-H contacts lead to the gecko effect where the Van der Waals attractive interaction makes the gauche conformation more favourable . Also there are six possible gauche conformers and only four possible APP conformers meaning the gauche arrangement is entropically favoured. The gauche structure was compared to the reference table and it was confirmed that this conformer is the lowest energy minima. The energy of the APP structure also agrees with the reference energy given in the table(https://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3).

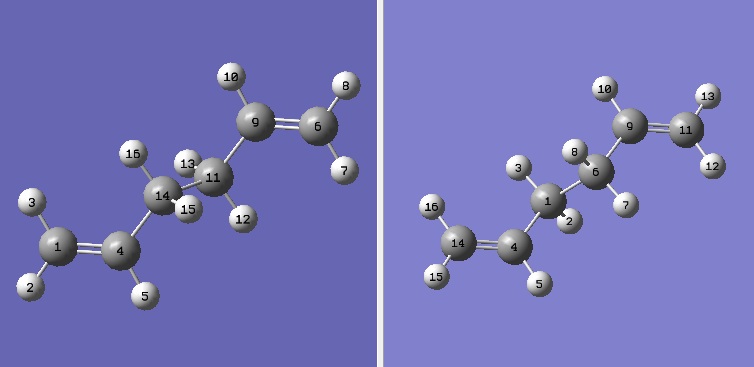
Another APP conformer (APP2) of 1,5-hexadiene was optimised at the HF/3-21G level of theory; this gave a structure with C_i symmetry and an energy of -231.69254 Hartree. This structure was then re-optimised to B3LYP/6-31G* level to give a structure with the same point group and an energy of -234.62318 Hartree. The structures look similar - both have a dihedral angle of 180 degrees. The carbon-carbon single bond lengths are slightly shorter whilst the carbon-carbon double bond is slightly longer in the structure optimised to a higher level c.f. the table below.

Comparing the optimised APP2 models

Bond	APP2 - HF/3-21G	APP2 - B3LYP/6-31G*
C=C	1.32	1.33
Central C-C	1.55	1.53
C-C	1.51	1.48

Vibrational frequencies are the second derivative of the potential energy and therefore minimal energy structures can be confirmed by vibrational analysis; if vibrational frequencies are real and positive this corresponds to a minimum point.

For the higher level calculation:
Low frequencies: - 38.2274, - 14.7195, 0.0006, 0.0009, 0.0010, 9.6799
Low frequencies: 73.4693, 74.1196, 119.5657

IR spectrum of the higher level calculation

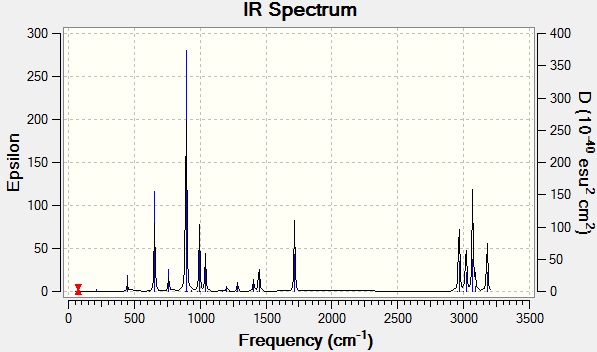
The vibrational analysis computes real properties:
Sum of electronic and zero-point Energies= -233.125690
Sum of electronic and thermal Energies= -233.118189
Sum of electronic and thermal Enthalpies= -233.117245
Sum of electronic and thermal Free Energies= -233.157407

The sum of electronic and zero-point energies is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE). The sum of electronic and thermal energies is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans. The sum of electronic and thermal enthalpies contains an additional correction for RT (H = E + RT) which is important when looking at dissociation reactions, and the last sum listed above includes the entropic contribution to the free energy (G = H - TS).

Optimising the Boat and Chair Transition Structures

The two possible transition structures (boat or chair) were optimised by
(1) by computing the force constants at the beginning of the calculation
(2) using the redundant coordinate editor, and
(3) using QST2. The reaction coordinate was visualised, the IRC was run and the activation energies for the Cope rearrangement.

Chair TS optimisation

Method: Computing the force constant matrix

Initially the delocalised allyl fragment (CH2CHCH2) was optimised (HF/3-21G) and two of these fragments were positioned in the assumed chair transition state with the two terminal carbons approximately 2.2 angstroms apart. The TS was optimised to a TS Berny by computing the force constant matrix (also known as the Hessian) in the first step of the optimization which was then be updated as the optimization proceeded. The opt+freq job type, Hartree Fock method, and the default basis set 3-21G were selected; the force constants were chosen to be calculated once with the additional keywords "Opt=NoEigen" to stop the calculation crashing if more than one imaginary frequency had been discovered. The optimised TS has a distance of 2.02 angstrom between the terminal carbons of each fragment. The frequency analysis showed one imaginary frequency at which corresponds to the Cope rearrangement at -818 cm^-1 (0dp).

Optimised Chair TS

Chair TS Vibration corresponding to the Cope Rearrangement

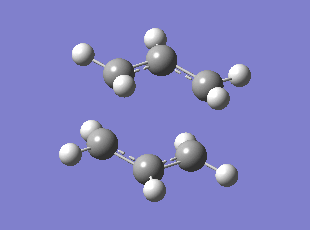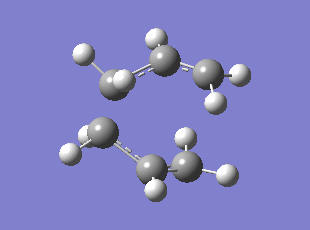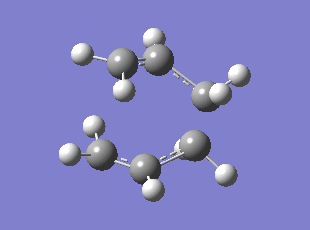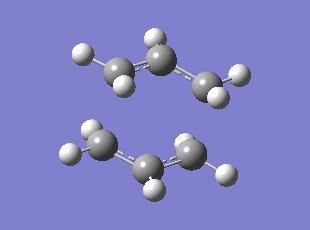
Method: Using the redundant coordinate editor

The TS was then optimised by freezing the reaction coordinate, using Opt=ModRedundant, and minimizing the rest of the molecule. Once the molecule is fully relaxed, the reaction coordinate is unfrozen and the TS optimization is started again. This method means that it may not be necessary to compute the whole Hessian once this has been done, and just differentiating along the reaction coordinate which can save time. Note again the Hartree Fock method and 3-21G basis set were used. The transition state optimisation was run with the frozen coordinates fixed (distance between the terminal carbons where a bond forms/breaks a bond during the rearrangement fixed to 2.2 angstroms), then repeated with the frozen coordinate bond as a derivative (no force constants calculated). This gave optimised distance between the two fragments as 2.02 angstroms which is in agreement with the TS (Berny) method, shown right; the two methods gave the same result.

Boat TS optimisation

Method: The QST2

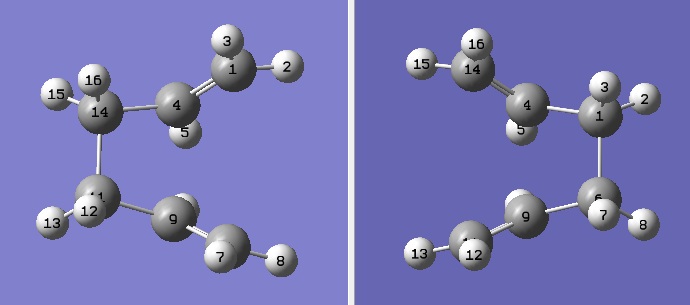
The boat TS was optimised using the QST2 method where the reactants and products are specified and the calculation interpolates between the two structures to find the TS between them. The numbering of the carbon and hydrogen atoms were manually changed so that they were numbered in the same way.

Labelled reactant (left) and product (right).

The fist QTS2 structure did not give the correct structure - this is because the calculation interpolated linearly between the two structures and translated the top allyl fragment to give a dissociated Chair TS. It was also necessary to manually change the orientation of the reactants and products so that the possibility a rotation around the central bonds was considered. For both the product and reactant, the central C-C-C-C dihedral angle was modified to 0 degrees, then the inside C-C-C bonds were reduced to 100 degrees.

Product and reactants with modified angles.

The above input was then optimised to a TS (QST2) using the Hartree Fock method and 3-21G basis set, this gave the TS with C-C distance of 2.14, 2.78 and 2.14 angstrom between the two fragments so that the middle carbons on each fragment are further apart. The optimised TS shows one imaginary frequency at -840 cm^-1(0 d.p.).

Optimised Chair TS

Boat TS Vibration corresponding to the Cope Rearrangement

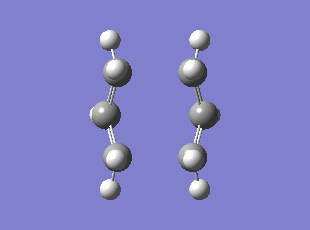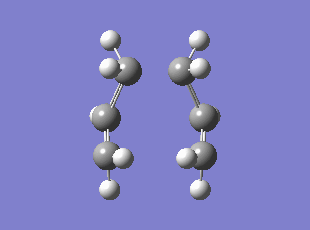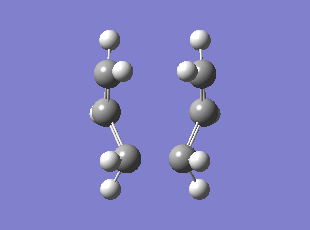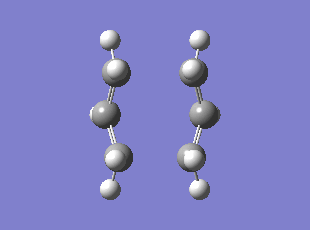
Method: Intrinsic Reaction Coordinate (IRC)

The IRC method can be used to predict what conformers of 1,5-hexadiene will develop from the optimised chair and boat transition structures. This method allows the minimum energy path,from a transition structure down to its local minimum on a potential energy surface, to be followed. This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest.

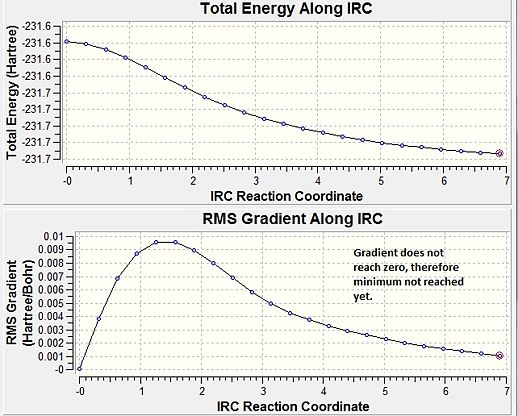
Force constants were determined once at the start of the calculation, and the reaction coordinate was ran in just the forward direction (since this is symmetrical), with 50 points. Initially a minimum is not reached; the gradient does not fall to zero. There are three ways a minimum can be reach:
(1) a normal minimisation can be run on the last point on the IRC,
(2) the IRC can be restarted with a large number of specified points until a minimum is reached
(3) the IRC can be re-done with force constants computed at every step.
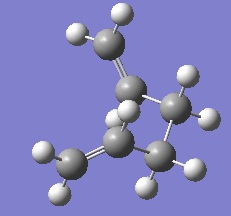
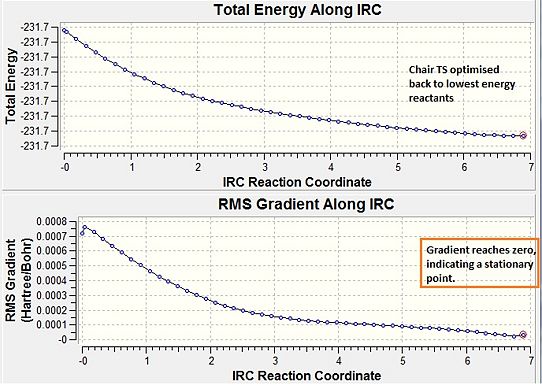
Although option three is not always feasible for large systems, it is known to be the most reliable therefore this option was chosen. IRC showed the chair TS to result in the gauche 2 structure (see Image below) with an energy of - 231.69166 au, the paths are illustrated graphically below.

Chair TS IRC leads to the Gauche 2 conformer


Graph 1: IRC method (force constants computed once) - minimisation not yet reached.

IRC - min not reached

Graph 2: IRC method (force constants always computed) - minimisation reached.

IRC - min reached

Calculating Activation Energies: re-optimising Boat and Chair TS to higher level of theory

The activation energies for the reaction via both transition states were calculated by re-optimising the chair and boat transition structures using B3LYP/6-31G* level of theory and carrying out a frequency analysis. Again one imaginary frequency which connects products to reactants was detected for each structure, showing that the structure is a TS.

Chair TS Imaginary Frequency (method:B3LYP/6-31G*)


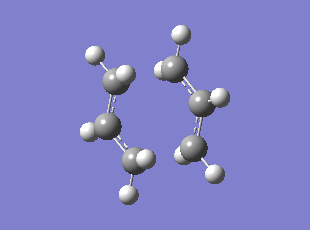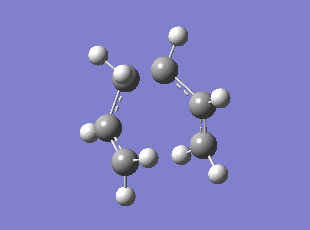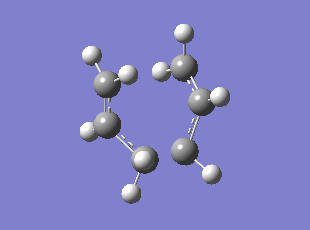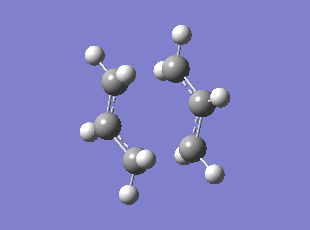
Boat TS Imaginary Frequency (method:B3LYP/6-31G*)

Comparing HF/3-21G and B3LYP/6-31G* optimised Boat and Chair TS

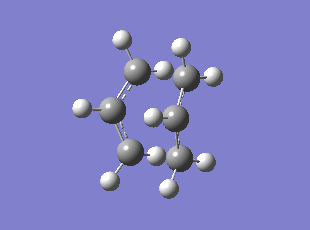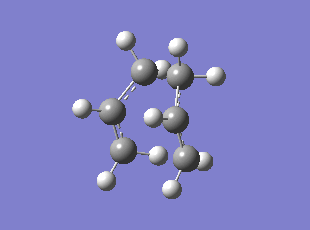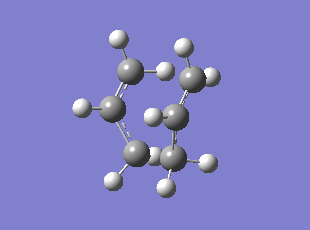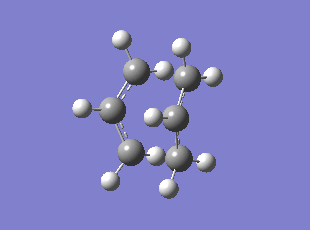
	Chair HF/3-21G	Chair B3LYP/6-31G*	Boat HF/3-21G	Boat B3LYP/6-31G*
Energy/ au	-231.61932	-234.56752	-231.60280	-234.55445
C-C distance through space between fragments/angstrom	2.02	1.98	2.14	2.24
Imaginary Frequency/cm-1	-818	-563	-840	-507

The geometries are similar but the there is a large energy difference between the two levels of theory, approximately 3 Hartree (~ Kcalmol^-1. As a result, usually the potential energy surface is mapped at a low theory level and then re-optimised at a higher level to provide more efficient calculations.

The activation energies at 0 Kelvin for the cope rearrangement were calculated by taking the difference between the energy of the reactant and the energy of the transition state.

Activation Energies at 0K (kcal/mol)

	HF/3-21G	B3LYP/6-31G*	Experiment
Chair	45.4	35.0	33±0.5
Boat	58.1	43.1	44.7±2.0

As the calculation is down to a higher level of theory, the activation energy values approach the experimental values. In order to completely match the experimental data an even higher level of theory would have to be used- the observed difference is due to the approximations made in the calculation.

The Diels Alder Cycloaddition

Exercise 1: MOs of Reactants

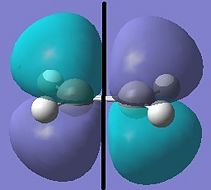
Cis-butadiene and ethylene were optimised using the semi-empirical method (AM1).

MOs of Reactants

Cis-Butadiene LUMO	Cis-butadiene HOMO	Ethylene LUMO	Ethylene HOMO
	HOMO B	HOMO B	HOMO B
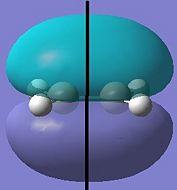symmetric	antisymmetric	antisymmetric	symmetric

Discussion of MOs

The [4s + 2s] pericyclic reaction between ethylene and cis-butadiene depends on the HOMO/LUMO interactions of the molecules. The concerted reaction is allowed if the HOMO of one reactant can interact with the LUMO of the other reactant and when the HOMO-LUMO interaction has significant overlap density. There is no overlap density if the orbitals have different symmetry properties. The HOMO of ethylene and the LUMO of butadiene are both symmetric with respect to the reflection plane and the LUMO of ethylene and the HOMO of butadiene are both antisymmetric. Therefore, the HOMO-LUMO pairs can interact and the principal orbital interactions involve the π/ π* orbitals of ethylene and the HOMO/LUMO of butadiene; π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene.

Exercise 2: Computation of the Transition State geometry

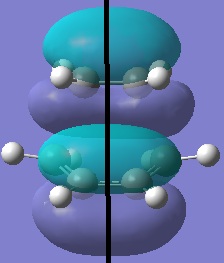
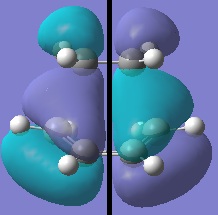
The transition state was optimised using the redundant coordinate editor (Opt=ModRedundant) - the reaction coordinate was frozen and the rest of the molecule minimised (distance between ethylene and butadiene set to 2.2 angstrom) then reaction coordinate was unfrozen and the structure minimised to a TS(Berny). The semi-empirical AM1 method was used.

MOs of Optimised Transition State

HOMO-1	HOMO	LUMO	LUMO-1
	HOMO B	HOMO B	HOMO B
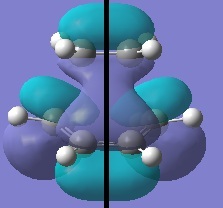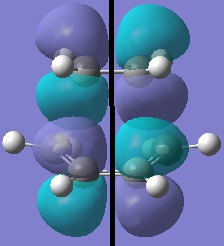symmetric	antisymmetric	symmetric	antisymmetric

Discussion of TS Geometry and MOs

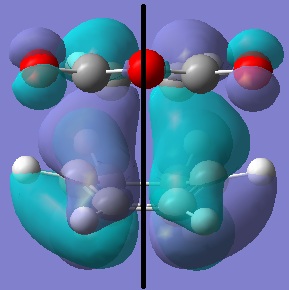
The antisymmetric HOMO of the transition structure, shown above, is formed from the HOMO of cis-butadiene interacting with the LUMO of ethylene. This reaction is allowed beaucse the two interacting orbitals have the same symmetry and significant overlap density.

Below is the optimsied TS with the bond lengths labelled

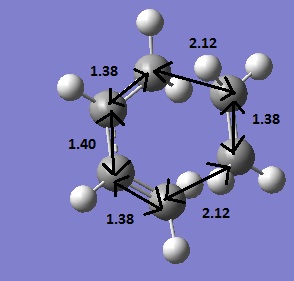
Typically, sp3 and sp2 carbon-carbon bond lengths are 1.54 and 1.34 respectively The TS shows intermittant bond lengths which suggests delocalised bonding within the TS. Carbon has an atomic van der Waals radius of 1.70Å therefore non-bonded carbons must be 3.4Å apart,the distance between the carbons on the fragments is less than this (2.12Å) which confirms a transition structure with partial bonds.

Disucssion Vibrational Analysis of TS

The structure was confirmed to be a TS by frequency analysis; the frequency analysis showed one imaginary frequency at -956cm^-1 which shows the synchronous formation of the two bonds(the reaction is concerted). The lowest positive frequency at 147cm^-1 shows twisting of the dieneophile fragment over the diene, unlike the imaginary frequency, the vibration does not bring the fragments inclose proximity and therefore will noit lead to a reaction path.

Transition State Imaginary Frequency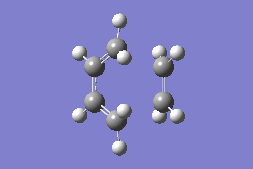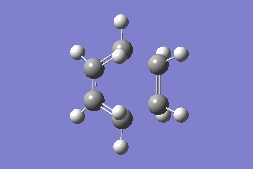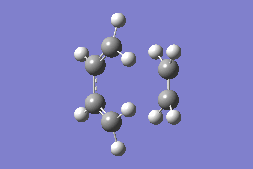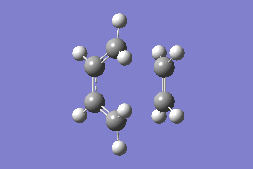


Transition State Lowest positive frequency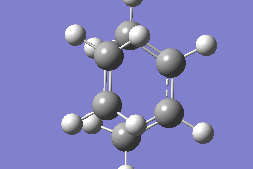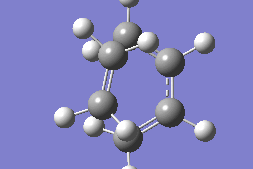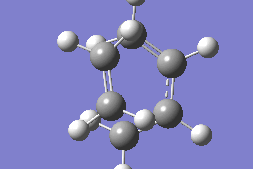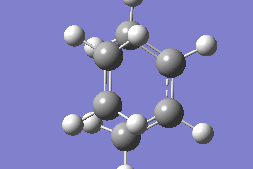

Exercise 3: The Regioselectivity of the Diels Alder Reaction

Cyclohexa-1,3-diene and maleic anhydride were optimised using semi-empirical AM1 method and then the TS was located using the redundant coordinate editor (the same method as in exercise two).

Comparing Endo and Exo Transition States

Endo	Exo
Optimised TS
Energy/au	-0.05159430	- 0.05050326
Interfragment Distance/ Angstrom	2.16	2.17
Imaginary Vibrational Frequency /cm-1	-806	-812
Animated maginary Vibrational Frequency

MOs of Endo TS

HOMO	LUMO
	EndoLUMO

MOs of Exo TS

HOMO	LUMO
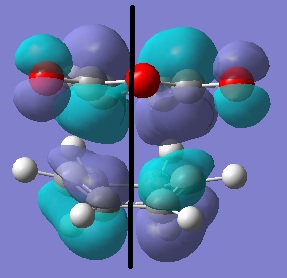	EndoLUMO

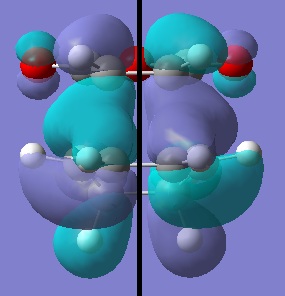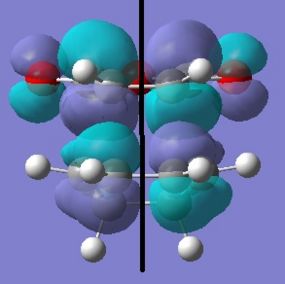Discussion

Although the endo- is thermodynamically less stable than the exo-product, the kinetic (endo) product dominates. The reason for this can be seen from examining the relative TS. The endo-TS is more stable than the exo-TS by aprroximately 0.001 au (~3 KJmol^-1. The exo-TS may be more strained due to steric repulsions between the oxygen atoms on the carbonyl groups and the hydrogens on the bridging sp3 carbons, which results in a higher energy TS. The lower energy of the endo-TS means the actiation energy is lowered and this is why the endo-product dominates.

By examinaning the HOMOs of each transition state, the lower energy of the endo-TS can be reasoned. The HOMO of the exo system has a node not present in the endo, consequently the endo has a more extensive electron cloud which leads to greater stability. In the endo, the pi bonding of the two fragments are on the same face of the molecule which leaves sigma bonding MOs on the other face that can interact together - this is caled secondary orbital overlap. In the exo, the pi and sigma bonding MOs cannot interact as they are now posotioned opposite each other resulting in a leading to a nodal plane.

Approximations and Errors

Calculated energies are accurate to ~10 kJ/mol, bond distances are accurate to 0.01 a.u, angles are accuarte to 0.1 degrees and vibrational frequencies have a 10% error and are quoted to whole numbers. Energies of moleucles should be considered relative to each other and not as absolute value. Only energies generated by the same basis set may be compared (i.e. to the same level of accuracy). The more functions included in the basis set the more precise the result.

The difference between experimental and compuational results in this investigation are due to approximations made during the calculations which increase as the number of functions in the basis set decrease. For example, the calculated activation energies for boat and chair cope rearranngement - the B3LYP/6-31G* level of theory was a lot closer to experimental values. Compuational caluclations also only consider the one particular moleucle drawn, where as in reality there are many moleucles whose conformers, although primairly the same e.g. gauche, app2, may differ slighlty.