Rep:Mod:certiorari3
Third Year Computational Chemistry Lab, by Simon Krautwald
Module 3 - The Transition State
While Module 1 and 2 mainly looked at the relative thermodynamic stability of stereoisomers or conformers, Module 3 will introduce the use of Gaussian for finding transition states of a reaction. By comparison of the energy of a transition state with that of the reactant, the activation energy for the process can be found. One can then predict which of two (or more) reaction pathways will be taken and thus predict the kinetic product of the reaction (rather than the thermodynamic product as in Modules 1 and 2). There are two sections in this module, an introductory tutorial presenting some new methods, and a second section investigating the transition states of the Diels Alder reaction.
Tutorial
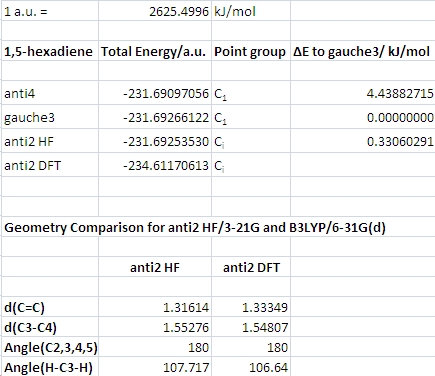
A structure for 1,5-hexadiene was drawn with the central C-C bond featuring an anti arrangement of the R groups and then cleaned up using the "Clean" function. It was optimized using Gaussian at the HF/3-21G level. The same was done for a molecule with a gauche conformation at the central bond. Pertinent data from the analysis of the results are presented in the table below. The gauche form can be expected to have the higher energy due to the smaller dihedral angle (60 degrees as opposed to 180) between the more bulky R groups on the central C-C bond.
The anti energy obtained agrees with that of conformation anti4 in appendix 1, the gauche one with that of gauche3. Interestingly, the gauche conformation is of lower energy than the anti conformation, and the gauche3 conformation obtained is actually the lowest energy conformation overall. There are two possible reasons for this. Either there is an electronic or steric effect stabilizing the gauche form or destabilizing the anti form, or the particular choice of basis set (3-21G) causes the gauche form to come out as more stable. It might well be that for another method and basis set, such as B3LYP/6-31G(d), the anti conformer is more stable. I am leaning towards blaming the basis set, because I cannot see any obvious geometrical distortion in this conformer that should make it higher in energy than the gauche form. It could be something to do with A1,2 and A1,3 allylic strain.
 |
 |
|---|
For the generation of the anti2 conformation with Ci symmetry, the optimized anti4 conformation was taken as a starting point. In anti4, one of the dihedral angles of four carbon atoms is almost zero degrees, whereas the other one is 114.534. The zero degree one was manually set to -114.534 degrees to approximately give the molecule a centre of inversion. HF/3-21G optimization then followed. The energy obtained agreed with the one quoted in appendix 1. After symmetrizing the structure (Default Tolerance), the point group was identified as Ci.
Some bond lengths, bond angles and dihedral angles for the HF and DFT results are presented in the table. There are no significant differences. The B3LYP/6-31G(d) optimized geometry was then submitted again in order to calculate the vibrational frequencies. The job summary indicated zero imaginary frequencies, which means that the geometry was really optimized to a minimum.
From the output file of the frequency job, the following data was obtained:
Sum of electronic and zero-point Energies= -234.469195 (Potential Energy at 0K, E = Eelec + ZPE)
Sum of electronic and thermal Energies= -234.461847 (Energy at 298.15K and 1 atm, E = E + Evib + Erot + Etrans)
Sum of electronic and thermal Enthalpies= -234.460903 ( H = E + RT, important for dissociation reactions)
Sum of electronic and thermal Free Energies= -234.500782 (includes entropic contribution to free energy, G = H - TS)
A new job was then submitted with the Freq=ReadIsotopes option enabled. Using this command, the temperature could be set to 0.00001 K and the pressure to 1 atm. Setting T = 0 exactly causes an error in the calculation, therefore it was set to 0.00001.
Sum of electronic and zero-point Energies= -234.469196
Sum of electronic and thermal Energies= -234.469196
Sum of electronic and thermal Enthalpies= -234.469196
Sum of electronic and thermal Free Energies= -234.469196
Note: The above data is for B3LYP/6-31G(d)! The values agree very well with those shown in the table in the appendix of the instructions.
These results are in line with expectations. When T = 0, there is some remaining vibrational energy (ZPE), but all thermal contributions are zero, so all the sums lead to the same result. For example, the second entry consists of the electronic energy and all the rotational, vibrational and translation contributions. At zero temperature, there are no excited states whatsoever accessible. It follows that all partition functions (representing the number of thermally accessible states or energy levels) are equal to 1, i.e. the molecule is in its absolute ground state.
Optimizing the "Chair" and "Boat" Transition Structures
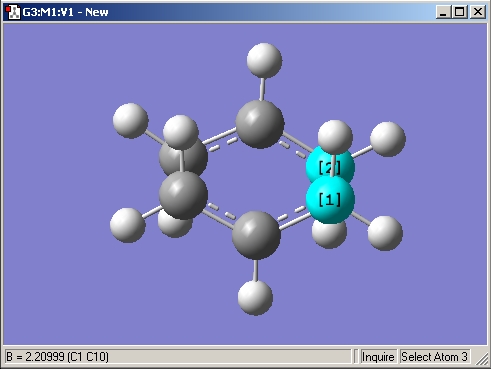
The allyl fragment was optimized at the HF/3-21G level. Following the instructions, the transition state of the Cope rearrangement was then set up manually by moving two allyl fragments into position. A picture of this is shown below. In it, the C-C distance of approximately 2.2 A is highlighted. Also, the chair shape, with all C-H bonds staggered, can be seen clearly. The TS optimization job was run and finished successfully - the summary indicated that there was one negative frequency of 817.977 cm-1.
The image below shows the 1st manually set up guess of the transition state. In the lower left corner, the C-C distance is indicated.
The vibration with the negative stretching frequency is one that brings one terminus on each allyl fragment very close to one terminus on the other allyl fragment, while the other two termini are moved further away from one another. This is the Cope rearrangement, the formation of one sigma bond at the expense of another one being broken.
</jmol> 3D view of the TS of the Cope Rearrangement
TSCopeRearrange |
Thermochemical Data for the Chair TS at B3LYP/6-31G(d)/a.u.:
Sum of electronic and zero-point Energies= -234.414930
Sum of electronic and thermal Energies= -234.409009
Sum of electronic and thermal Enthalpies= -234.408065
Sum of electronic and thermal Free Energies= -234.443815
Thermochemical Data for the Boat TS at B3LYP/6-31G(d)/a.u.:
Sum of electronic and zero-point Energies= -234.402342
Sum of electronic and thermal Energies= -234.396008
Sum of electronic and thermal Enthalpies= -234.395063
Sum of electronic and thermal Free Energies= -234.431097
Again, these values agree very well with those shown in the appendix.
 |
 |
|---|---|
 |
 |
The above table with four images shows snapshots that were taken during the part dealing with the optimization of the boat transition state.
The first QTS2 optimization at HF/3-21G failed. An image is included showing the reason. Gaussian merely tried to connect the termini of the two allyl fragments from the geometry it was given, it did not rotate about bonds to find a chair or boat transition state. Hence the "crossover" or X-shaped transition state. d(C1-C6) = 4.32553 d(C3-C4)=3.48200, much longer than any forming or breaking C-C bond would be in reality, and much longer than the 2.02 A found for the chair TS using the above methods.
The starting geometry was then manipulated (central dihedral angle to zero degrees, selected bond angles to 100 degrees) in order to manually fold the structure into a boat geometry. Repeated optimization then succeeded. A snapshot of the animated vibration with negative stretching frequency is shown with the title "Vibration in Cope Boat TS". One can clearly see the boat conformation, and two of the carbons are quite close to one another (bond forming), while two others are quite far apart (bond breaking). Relevant data for both transition states is shown in the table below. The chair transition state is about 36 kJ/mol lower in energy than the boat. This is in good agreement with the values presented in the appendix; shown below is their conversion into kJ/mol.
41.32 kcal/mol - 33.17 kcal/mol = 8.15 kcal/mol = 34.12 kJ/mol
The Diels Alder Cycloaddition
The frontier molecular orbitals of butadiene are presented in the table below. The HOMO is antisymmetric with respect to the plane bisecting the central C-C bond, the LUMO is symmetric:
HOMO - a
LUMO - s
 |
 |
|---|
This means that in any Diels Alder reaction of butadiene, either the HOMO of butadiene will have to overlap with an antisymmetric LUMO on the dienophile (such as the Pi* on ethylene) OR the LUMO of butadiene will have to overlap with a symmetric HOMO on the dienophile (such as the Pi orbital on ethylene). Which of the two processes is envisaged to happen usually depends on how electron rich or deficient the components are. For a normal electron demand DA, the diene is the electron rich component and the dienophile contributes the electron deficient double bond (as in the case of maleic anhydride).
 |
 |
|---|---|
 |
 |
 |
 |
The HOMO of the transition state is still antisymmetric with respect to the plane bisecting the central bond, and the LUMO is still symmetric. This is the essence of the conservation of orbital symmetry. The orbitals involved in a pericyclic reaction have a certain symmetry to start with, they maintain that symmetry in the transition state, and in an ideal case the reactant orbitals smoothly transform into orbitals of the product with the same symmetry. Throughout the process, the symmetry of the orbitals is conserved.
In this case, the HOMO of the TS is formed from the HOMO of butadiene and the LUMO of ethylene as shown in the picture. One can clearly see that between each of the pairs of carbon atoms that form a new bond, there is an orbital lobe of one phase, which means that there is a bonding interaction. It was a key insight that many pericyclic processes are facile because throughout the reaction the maximum possible bonding is being maintained.
The average lengths of C-C bonds are as follows:
C-C single bond: 1.54 A
C-C double bond: 1.34 A
C-C triple bond: 1.20 A
C-C in benzene: 1.40 A
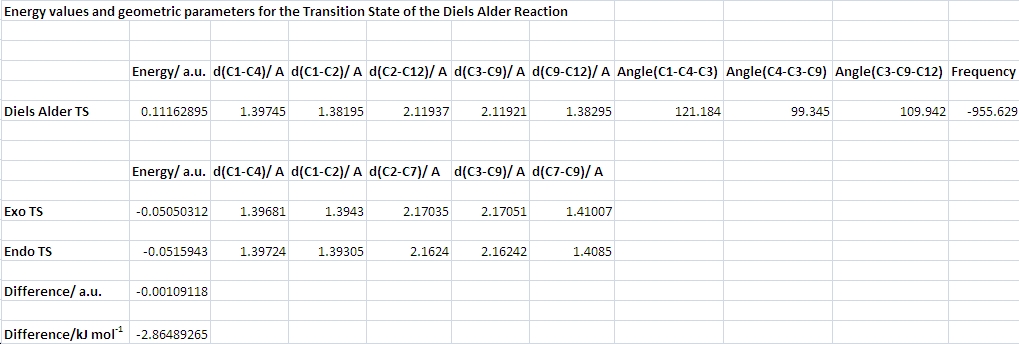
The table presents energies and geometrical parameters of the three DA transition states modelled. For the butadiene+ethylene system, the average bond length is about 1.38 A, i.e. significantly shorter than a single bond and somewhat longer than a C=C double bond. The two bonds that are being formed with a C-C distance of about 2.12 A are much longer than a typical C-C single bond.
 |
 |
|---|---|
 |
 |
The transition state was modelled according to the first method described in the instructions. The bicyclo[2.2.2]octane ring system was drawn and two methylene groups removed. This gave the "envelope" structure of an ethylene molecule approaching a butadiene molecule from the top face. The length of the two forming bonds was set to 2.2 A. This seemed like a reasonable value, as it had worked for the Cope rearrangement. A job of the type opt+freq with the AM1 method was started. Optimization to a TS (Berny), calculation of force constants once, and opt=noeigen. The job completed successfully with one imaginary frequency (indicating that Gaussian minimized to a TS) of -955.629 cm-1. Animating this vibration showed the atomic motion corresponding to and expected from the Diels Alder cycloaddition. The atoms of the ethylene molecule close in on the terminal atoms of butadiene in a concerted fashion. Pertinent geometrical data of the transition state are presented in the table.
The lowest positive frequency is 146.95 cm-1.
It is interesting to note that the bond lengths of a group of four bonds (that does not include the two new sigma bonds being formed) are almost equal at 1.38-1.39 A, intermediate in length of a C-C single and double bond. This partial bond length equalization supports the concept of an aromatic transition state!
The energy of the exo TS is only about 3 kJ/mol higher than that of the endo TS. Although this is qualitatively correct (or else we wouldn't observe the endo product), the method and basis set used clearly do not give a result that agrees with experiment. A difference of only 3 kJ would lead to a mixture of products, one would need a difference of at least 10 kJ/mol to observe the endo product exclusively. Given that the semi empirical AM1 method is extremely fast, this result can be understood/excused.
References Mini Project
1. A. Neugebauer, G. Häfelinger, Int. J. Mol. Sci., 2005, 6, 157
2. Arduengo, A. J. et al., J. Am. Chem. Soc., 1991, 113, 361
3. A. J. Arduengo et al., J. Am. Chem. Soc., 1992, 114, 5530-5534
4. W. A. Herrmann, Angew. Chem. Int. Ed., 2002, 41, 1290
5. W. A. Herrmann et al., Angew. Chem. Int. Ed., 1992, 31, 1485
6. G. Frenking, C. Boehme, J. Am. Chem. Soc., 1996, 118, 2039-2046