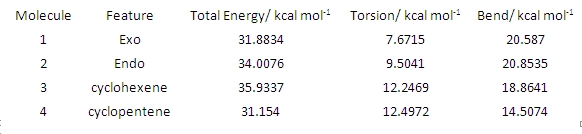Rep:Mod:certiorari
Third Year Computational Chemistry Lab, by Simon Krautwald
Module 1
Modelling using Molecular Mechanics
The following four exercises will use the Allinger MM2 molecular mechanics models in ChemBio3D to investigate selected chemical curiosities. The key to understanding these generally lies in the geometry and conformation of the molecule in question rather than stereoelectronic or other molecular orbital effects (e.g. aromaticity, FMO interactions). This means that the bulk of the discussion will focus on bond angles, torsional strain, steric interactions and similar concepts. Therefore, no advanced quantum mechanical calculations of the electronic structure are required.
The Hydrogenation of Cyclopentadiene Dimer
Cyclopentadiene dimerizes in a Diels Alder reaction to give the kinetic endo product 2. This is because the endo transition state is lower in energy than the corresponding exo transition state, so 2 is formed faster than 1. The exo dimer is the thermodynamic product as it is more stable (see energy values in the table below).
Why should the exo diastereomer be the more stable? A look at the contributions which make up the total energy of the molecules 1 and 2 gives an answer to this question. The calculated energy difference of 2.1 kcal/mol appears to be almost entirely due to the torsion contribution (see table). The torsion term is a measure of the deviation of all the dihedral angles of the molecule from their ideal values and, in an analogous way, the bend term reflects the deviation of all the bond angles from their ideal values.
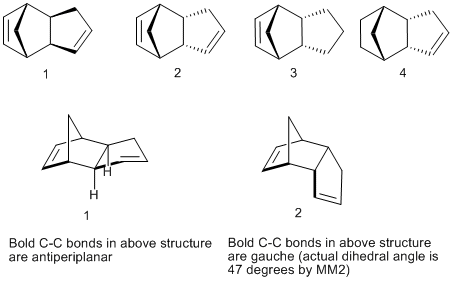
Thus, they put a number to the conformational or geometrical strain inherent in a molecular structure. We can associate the lower energy of the exo isomer with the fact that the bold C-C bonds indicated in 1 are almost antiperiplanar, whereas they are gauche (47 degrees compared to the ideal 60) in the endo isomer 2. Thus, in 2, there is more Pauli repulsion due to the smaller dihedral angle and therefore the molecule is less stable than 1.
3 and 4 are the potential products of partial hydrogenation of 2. Comparing their MM2 energies, 4 is thermodynamically more stable by about 4.5 kcal/mol. This time, it appears to be almost entirely due to a lower bend term. This suggests that the bond angles in 3 (cyclohexene) deviate more from their ideal values than the ones in 4 (cyclopentene).
For Molecule 3 (Hydrogenation in five membered ring)
107.579 degrees is the angle of C=C-C for the double bond in the six-membered ring. This is a significant departure from ideal sp2 geometry. The angle of H-C=C is 127.149 degrees. In the five-membered ring, the deviation from ideal sp3 geometry for C-C-H angles is 1 to 3 degrees.
For Molecule 4 (Hydrogenation in six membered ring)
Now that the two carbons are sp3, the bond angles are off by only 1 degree (110 instead of 109), i.e. hydrogenation of the double bond in the six membered ring is accompanied by a significant relief of strain. In the five membered ring, the angles are as follows:
124.3805 for double bond C=C-H instead of 120 in the ideal case
112.4265 for double bond C=C-C instead of 122 in the ideal case
(as given by Structure-Measurements-Generate all bond angles)
Clearly, the bond angles in 3 deviate more from ideality (e.g. 107 instead of 120) than those in 4, so 4 is the more stable molecule.
These results withstand the sanity check, even without knowing exact bond angles after a molecular mechanics optimization, one would intuitively say that the more stable molecule is the one in which the double bond that is part of two ring systems is hydrogenated, leaving a relatively unstrained double bond in the five-membered ring.
Thus, if the first hydrogenation is under thermodynamic control, we expect 4 to be the product. However, the double bond in the five-membered ring is potentially sterically more easily accessible and might thus hydrogenate faster, so if the reaction is under kinetic control, 3 will be the initial product.
Nucleophilic Attack on Pyridinium Rings
When enantiomerically pure compounds 5 and 7 are reacted with the nucleophiles MeMgI and PhNH2, respectively, products 6 and 8 are obtained. In both cases the stereochemical outcome is interesting, since it is clear that in both cases one face of the pyridinium ring is favoured over the other. The aromatic ring itself is of course flat, so some feature of the structure of the rest of the molecule must force the incoming nucleophile to discriminate between the otherwise equivalent faces of the aromatic ring.
The 3D structures of 5 and 7 are not immediately obvious, so molecular modelling at the MM2 level was used to optimize the geometry of reactants and products. Jmol files of compounds 5 and 7 have been included to illustrate the arguments brought forward in this discussion.
Total Energy of 5: 26.3165 kcal/mol
Total Energy of 6 Me up: 28.8784 kcal/mol
Total Energy of 6 Me down (not observed): 28.2485 kcal/mol
As can be seen from the above values, the isomer that is not formed in the reaction is actually slightly more stable. The reaction is irreversible and gives the one product which forms very much faster than the other isomer due to the factor discussed below.
When MeMgI is included in the MM2 optimization, an error occurs. This is because the Molecular Mechanics programme cannot handle the metal atom, which is not parametrized.
What is immediately striking about the optimized structure of compound 5 is that the carbonyl group does not lie flat in the same plane as the pyridine ring. This is odd; without considering the geometry of the rest of the molecule, one would expect the amide linkage to be flat so that Pi delocalization is maximized. There is a trade-off between the seven membered ring trying to adopt the most favorable conformation and the Pi system to be flat. The compromise results in the carbonyl group being tilted so that the oxygen sticks out above the plane of the benzene ring, which can be seen for compound 5 in the Jmol applet below.
3D view of compound 5
Compound5 |
The dihedral angle between the two aromatic Cs, the C and O of CO is 24.8744 degrees. This is a quantitative result for the geometry of the carbonyl group.
3D view of compound 5, (R)-proline
Compound5Unnatural |
The tilting of the CO group suggests a mechanism for the asymmetric induction. Initially, I thought that the optically pure proline might result in a bent molecule with a clear endo and exo face and that then delivery of the Me would be more facile from the accessible exo face. However, on inspecting the 3D model no such structural feature is found. The methyl adds from the top face, this observation along with the result that the oxygen is above the plane of the aromatic ring suggests that an oxygen lone pair chelates/coordinates to the magnesium atom in the Grignard reagent and thus directs it to attack from the top face exclusively.
The MM2 optimization of compound 7 terminated in error. The resulting structure had a benzene ring that was not flat. Discussion with other students suggested some had had similar problems, which were resolved by re-drawing the structure from scratch. This was tried, to no avail. Nonetheless, a 3D Jmol view of the molecule is shown below. Clearly, the carbonyl oxygen is now tilted so that it is pointing below the plane of the aromatic. In line with the argument above, I surmised that hydrogen-bonding of the nucleophilic aniline to the carbonyl oxygen might direct it to attack from the bottom face. This, however, is not observed experimentally, which in turn suggests that now steric hindrance is the factor dominating the stereoselectivity. The aniline molecule attacks the less hindered face of the aromatic system, which is the top face, and thus ends up syn to the existing methyl.
3D view of compound 7
Compound7 |
An Intermediate in the Synthesis of Taxol
There exist conformers which have such restricted rotation about a single bond that the different conformers can actually be isolated. These conformers are called atropisomers, and the phenomenon is called atropisomerism accordingly. The classic example are ortho-disubstituted biphenyls, in which rotation about the single bond connecting the two aromatic rings is very slow due to the steric clash between the ortho substituents.
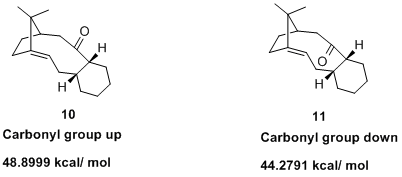
In 1991 Leo Paquette published research describing reversible oxy-Cope rearrangements, and one point of discussion was the atropselective anionic ocy-Cope rearrangement of a carbinol that produced a structure almost identical to 10 and 11.
In the following it will be discussed why one atropisomer is more stable than the other and why the alkene in 11 reacts unusually slowly.
| Molecule | Feature | Total Energy/ kcal mol-1 | Torsion/ kcal mol-1 | Bend/ kcal mol-1 |
|---|---|---|---|---|
| 10 | CO up | 48.8999 | 18.3113 | 15.8321 |
| 11 | CO down | 44.2791 | 19.6602 | 10.6943 |
The initial MM2 optimization of both isomers resulted in the six-membered ring adopting a boat/ twist-boat conformation. This was unsatisfactory, so the ring's conformation was manually forced to be that of a chair. Another MM2 run then gave the energies and geometries reported in the table above, which were approximately 6 kcal/mol lower in energy than the boat energies.
So why is the atropisomer with the carbonyl group pointing down more stable? Again we look for one term among all the contributions that is significantly different and might thus give us a clue as to the origin of the difference in stability. Sure enough, the bend term in 10 with the CO group up is 15.8 kcal/mol; in 11 with the CO group down it is 10.7 kcal/ mol. Torsion and the other parameters are rather similar. Thus, the higher angle strain in 10 results in its relative instability. Using the ChemBio3D programme to look at the angles around the carbonyl group is easy and quickly gives insight. For the CO group to point upwards, the sp2 bond angles have to deviate quite markedly from their ideal values (see table). When it points downwards, the actual angles are quite close to their ideal values. This comes at low cost, namely that the dihedral term in 11 is larger than that in 10 by about 1 kcal/ mol.
| 10 CO up | 11 CO down | ||||
|---|---|---|---|---|---|
| Actual | Ideal | Actual | Ideal | ||
| C-C-C | 126.2394 | 116.6 | 120.297 | 116.6 | |
| C-C=O | 115.3309 | 122.5 | 119.6095 | 122.5 | |
| C-C=O | 118.0654 | 122.5 | 119.9807 | 122.5 |
This type of behaviour – accepting an unfavourable increase in torsion to relieve angle strain, or vice versa – is not unusual. It is familiar from simple examples in introductory conformational analysis, where e.g. the cyclobutane molecule is shown to adopt a puckered wing conformation, thereby relieving some of the dihedral strain resulting from the eclipsing interactions and increasing the angle strain so that the net result is the stabilization of the molecule.
Paquette’s intermediate in the taxol synthesis is a so-called bridgehead alkene. In regular-sized rings (e.g. six-membered) these are so strained and unstable that they don’t exist (Bredt’s rule). This is backed up by the observation that e.g. norbornane carbocations never eliminate to form bridgehead alkenes, simply because the sp2 centre would not be planar. The bridgehead alkene at hand only exists as it is part of a nine-membered ring. This larger ring can actually adopt a conformation that accommodates the geometrical demands of a double bond – this can be seen by generating all the bond angles after the MM2 optimization. The results show that the angle between the bridging methylene, the bridgehead carbon and another carbon of the five-membered ring is 108 degrees instead of ideal 117. The other bond angles around the alkene do not deviate more than a few degrees from their ideal values. This data suggests that the alkene is somewhat strained, but not to an extent that would make its existence impossible.
It was found experimentally that the bridgehead alkene reacted abnormally slowly. Initially, this is of course against the chemist’s intuition. If anything, one would expect the slightly strained alkene to react a little faster than an analogous straight chain alkene with similar substitution pattern.
Is the origin of this reduced reactivity kinetic or thermodynamic stability? Looking at the 3D structure of the molecule does not indicate any steric shielding of the alkene, the approach of other species appears to be unhindered. When the alkene reacts, the arrangement of substituents around the sp2 carbon atoms must become tetrahedral. I think that the bridgehead carbon atom in particular cannot simply pyramidalize because of its position as bridgehead and member of two rings. In a free chain, the rest of the molecule can easily rotate to allow this change of arrangement around the carbon atom. In this example, on the other hand, this rotation to accommodate the new geometry results in significant strain in the five-membered ring. The transition state leading to the alkane is therefore relatively high in energy and thus the functionalization of the alkene (e.g. hydrogenation, epoxidation...) proceeds slowly.
The above argument uses the molecule’s conformation/ shape to explain the observed kinetic behaviour. In 1981, Maier and Schleyer reported that bridgehead alkenes in medium-sized polycyclic ring systems can be expected to be hyperstable, i.e. have negative olefin strain energies. This essentially means that the alkene is more stable than the corresponding hydrocarbon. The subject was discussed in depth again in 1986 by McEwen and Schleyer1 and more reviews and contributions can be found by searching for “hyperstable alkenes” on http://pubs.acs.org. In their 1986 publication, they even predicted bridgehead alkenes that are so stable that they have positive heats of (cis) hydrogenation, i.e. hydrogenation of these alkenes is predicted to be endothermic.
The hydrogenated version of molecule 11 (carbonyl pointing down) was optimized using an MM2 force field with ChemBio3D. The total energy turned out to be 49.5185 kcal/mol. Thus in the hydrogenated molecule the total energy is a bit higher but there is no immediately obvious feature that would allow you to judge this molecule as being much less stable than the alkene. Calculations at a higher level are probably necessary to be able to compare the two molecules.
References
1. McEwen, A; Schleyer, P. v. R., J. Am. Chem. Soc., 1986, 108 (14), 3951-3960. DOI: http://dx.doi.org/10.1021/ja00274a016
How One Might Induce Room Temperature Hydrolysis of a Peptide
In mid 2008 a reaction was reported that cleaved unactivated, unstrained peptide bonds very fast at neutral pH. Considering the remarkable thermodynamic stability of the amide moiety, this is no mean feat. The intramolecular "hydrolysis" reaction is presented in the figure below. MM2 molecular modelling proved useful for comparing the relative energies of different conformations of 13 and 14, respectively, and for visualizing the geometry of attack. The cause of the dramatic increase in rate will be discussed, and a Jmol file of 13 is included so that a 3D view of the structure is possible.

The conformer of 13 with the amide and alcohol in equatorial positions is more stable by about 6 kcal/ mol. This is of course due to the reduced 1,3 diaxial interactions when the bulky substituents are equatorial. There can also be good hydrogen bonding from OH to carbonyl C because OH is a good hydrogen bond donor and C=O is a good hydrogen bond acceptor. The hydrogen bond certainly contributes to the stability of the all-equatorial conformer; however, it is not taken into account by the MM2 programme. Now, the “hydrolysis” of this peptide bond (the formation of the lactone) is so much faster in 13 and 14 because it is a unimolecular reaction, not a bimolecular reaction like normal peptide hydrolysis. This means the rate law depends only on the concentration of 13 or 14, the reaction is easier entropically and due to the hydrogen bond the reacting centres are generally close together.
Furthermore, looking at the Jmol model shown below, one can see by careful rotation of the molecule that the atoms that will make up the new six-membered ring are already folded up in a chair like structure. The carbonyl group only has to rotate slightly to allow attack of the hydroxyl group along the Buergi-Dunitz trajectory. All of this combined makes hydrolysis in the all equatorial conformer of 13 very fast. Finally, thermodynamic stability of the product, with another six-membered ring, might contribute to pulling the equilibrium over to the side of the lactone.
14 is a little more stable than compound 13 (both with amide in axial position) due to the trans ring junction, which is more stable than a cis junction between two six-membered rings. However, 14 is conformationally not flexible (it cannot ring flip), so the molecule’s shape is permanently such that the OH is not in a good position to attack CO.
Only axial amide 14 will be able to form the lactone, but axial 14 is the minor conformer by quite a large margin, and the more stable equatorial 14 cannot ring flip into the reactive conformation since the trans-decalin is rigid. This explains the huge difference in observed rates of hydrolysis.
As is pointed out in the paper1, the amides 13 and 14 are unstrained, i.e. there is no A1,3 allylic strain which causes the rate enhancement. This suggests that the rate enhancement must be due to some other feature of the molecule - as explained above.
3D view of compound 13
Compound13 |
References
1. M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, J. Org. Chem., 2008, 73, 6413–6416 DOI: http://dx.doi.org/10.1021/jo800706y
Semi-Empirical MO Theory - Regioselective Addition of Dichlorocarbene
As an introduction to quantum mechanical calculations, the electronic structure and vibrational frequencies of compound 12 were computed using a density functional B3LYP/6-31G(d) approach. The geometry of 12 was pre-optimized using MM2 and HF/STO-3G and a job was then submitted to the SCAN for the DFT computation. The frontier molecular orbitals of 12 have been visualized using Gaussview, and in the following discussion some derivatives of 12 will be invoked to illustrate certain points about the electronic structure.
3D view of compound 12, DFT optimized
Chlorodiene |
From top to bottom: HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2
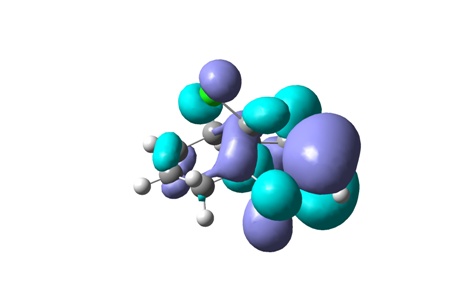
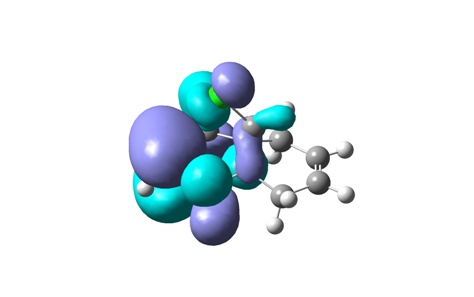
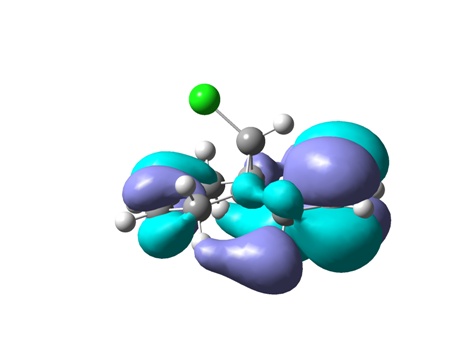
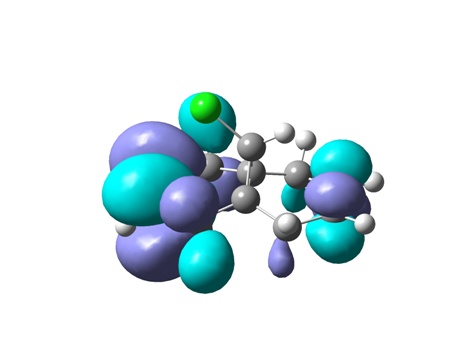
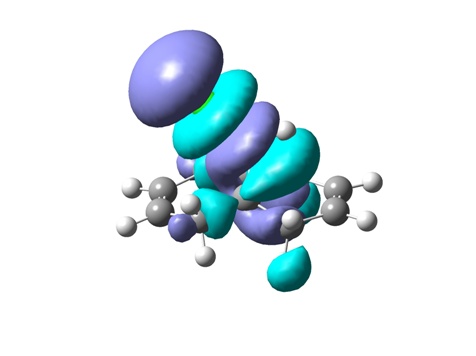
The geometry of the optimized chlorodiene molecule is generally very strained, irrespective of the optimization method used (MM2, HF STO-3G, RB3LYP 6-31G(D)). In all 3D models it is clear that the cyclopropane ring effectively forces the two six-membered rings to adopt unfavourable conformations. Cyclohexenes prefer to adopt half chair geometries; in the case at hand, this is not possible. The cyclohexenes are almost flat.
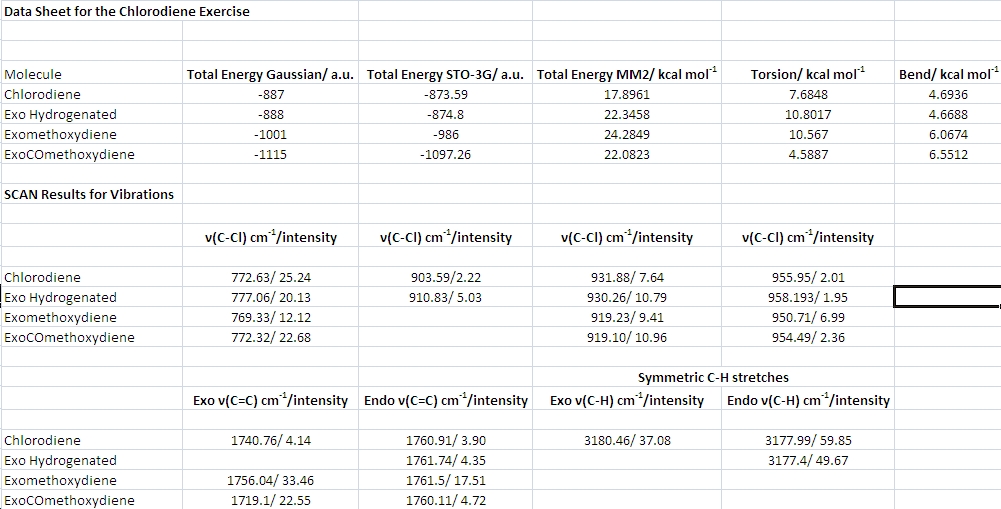
The table above shows the data collected using the three approaches as well as the results of the vibrational frequency calculations for the chlorodiene molecule 12 and three of its derivatives: one with the exo double bond hydrogenated, the next one with a methoxygroup on the double bond and the third one with a carbonylmethoxy group. These three molecules were investigated in order to probe whether there is any electronic interaction between the exo double bond and the C-Cl antibonding orbital.
It was found after the DFT optimization on the SCAN that the exo double bond had a stretching frequency of 1740 cm-1, whereas that of the endo double bond was 1760 cm-1. This is about 100 cm-1 higher than the real stretching frequencies of C=C double bonds, which, depending on their degree of substitution, are found between 1600 and 1680 cm-1.
The 20 cm-1 difference is significant enough to arouse suspicion. Why should the exo double bond be weaker? Geometrically (bond angles, dihedral angles) the two rings are very similar, so the origin is likely to be electronic in nature. Rzepa pointed out in that the exo Pi orbital can overlap with the C-Cl sigma * orbital. This would explain why the exo double bond is a little weaker (electron density is donated into another orbital), and it would suggest that the C-Cl bond has a higher stretching frequency in the diene than in the derivative in which the exo double bond is hydrogenated. If the effect is very pronounced, one might even wish to measure the distance between the double bonds and the cyclopropane carbon atom bearing the chlorine atom to find out whether this particular C atom is maybe a little closer to the exo than to the endo double bond (indicating a weakly bonding interaction).
Inspecting the above table, it can be seen that the hydrogenated molecule is indeed expected to have slightly higher v(C-Cl) stretching frequencies. This suggests that the orbital interaction is rather weak. To ensure that the result is reproducible, two more derivatives were optimized and subjected to frequency calculations, one with an electron donating methoxy substituent on the exo double bond, the other one with an electron withdrawing carbonyl group. Interestingly, the DFT optimization on the SCAN oriented the carbonyl group in such a way that it was flat with regard to the double bond, thus enabling conjugation. During the MM2 optimization of the molecule, this feature had to be set manually, again an indication of the inadequacies of the Molecular Mechanics method for certain problems.
The methoxy substituent clearly increased the C=C bond strength (higher v(C=C) of 1756 cm-1, as it increases the electron density between the two carbons), whereas the carbonyl group decreased it to 1719 cm-1 due its electron withdrawing effect. This is in line with expectations.
The methoxy substituent also caused a slight decrease in v(C-Cl), in line with increased donation of electron density into the C-Cl sigma* orbital.
The carbonyl substituent, however, had no such effect.
Both the HF STO-3G and the B3LYP optimization computed the molecular orbitals of compound 12. The results were similar, although those of the more advanced technique appeared aesthetically more pleasing in GaussView.
Visualizing the surfaces, the expected result would be seeing an opportunity for constructive overlap between the HOMO-1 (exo Pi orbital) and the LUMO+2 (C-Cl sigma*). Unfortunately, this is not borne out. Although there is clearly the possibility of overlap, this would be antibonding. This result does not agree with the computations done by Rzepa et al. The surfaces for the HOMO-1 through to the LUMO+2 are shown.
In terms of reactivity, the stabilization of the exo double bond by delocalization into the C-Cl sigma* orbital means that the endo Pi bond is the HOMO (although the displayed surfaces do not suggest any bonding overlap, it is clearly taken into account – looking at the list of MOs in GaussView indicates the endo Pi bond as being the HOMO). The computations by Rzepa thus rationalize why the dichlorocarbene (an electrophilic six electron species) adds to the endo double bond rather than the exo one.
DFT-based Molecular Orbital Methods - Miniproject
This section will introduce the use of Density Functional Theory (DFT) based calculations of the (electronic) structure of molecules. The aim was to optimize the geometries of two isomers formed in one reaction using a DFT method and then submit the optimized geometries as another job on the SCAN to predict the 13C NMR spectra of both compounds. The key point here is to investigate whether it is possible to accurately predict the spectra as well as the spectral differences between two compounds so that experimental assignment is made easy. A reaction not given in the script was studied, therefore, there will also be comments on its synthetic utility, mechanism and the origin of its remarkable stereocontrol.
Looking for a suitable reaction
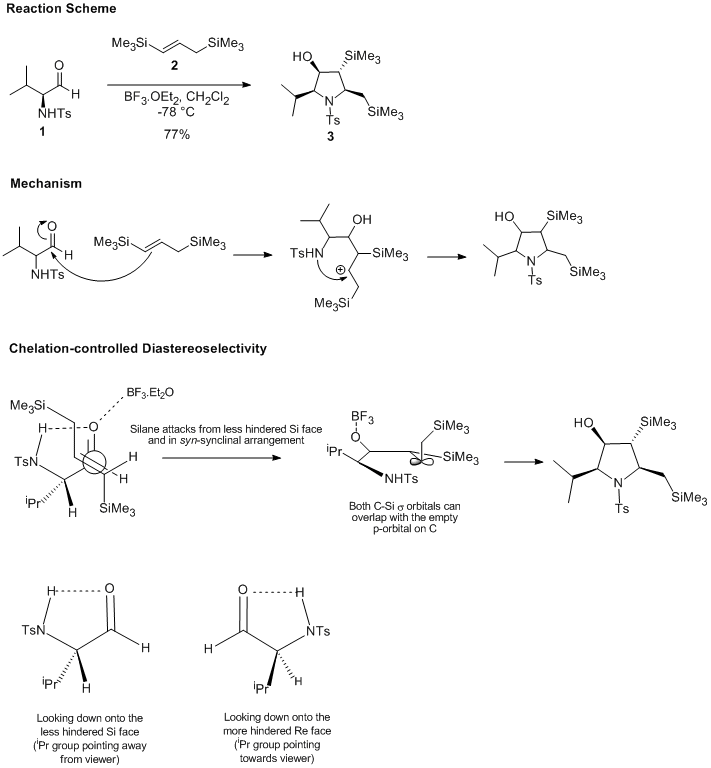
Initially, I looked at Nicolaou's and Sorensen's Classics in Total Synthesis. Naturally, I found very many suitable examples, but I could not pursue any of them because either 13C NMR was not yet commonly used or the supporting information was unavailable. Many of the very modern total syntheses by groups such as the Nicolaou or Overman groups were too complex – all the intermediates very big molecules with many accessible conformations. Then I searched for the keywords “stereoselective synthesis” on http://pubs.acs.org, having in mind finding a selective aldol reaction. The problem here was again the complexity and conformational ambiguity of the substrates. It was then that I found the reaction I eventually chose: a stereoselective synthesis of functionalized pyrrolidines reported in 2006 by Restorp, Fischer and Somfai1. It appeared to be a good choice because the penta-substituted pyrrolidine is conformationally rather rigid (which is important for the 13C NMR shift prediction). Furthermore, the reaction employed silane chemistry which I had not come across yet and it was therefore inherently interesting. The stereoselectivity is almost complete; this makes the reaction useful and the outlook of understanding the stereoselectivity motivated me to investigate the reaction. The scheme below shows the reaction mechanism and a rationalization, both of which were adapted from the original paper.
The reaction is an annulation of N-Ts-alpha-amino aldehydes and 1,3-Bis(silyl)propenes. As shown in the mechanism section, the allyl silane initially attacks the Lewis acid complexed carbonyl group which gives an intermediate beta-silyl cation. The double bond does not open in the direction that would give an alpha-silyl cation. The sulfonamide nitrogen of the amino aldehyde then traps the carbocation in a cyclization that gives the pentasubstituted pyrrolidine with very high stereocontrol. Densely functionalized pyrrolidines such as this one are commonplace targets in organic and medicinal chemistry, and efficient routes to them are therefore of value. Furthermore, the dimethylphenylsilyl group is a known hydroxyl group synthon, so after annulation the polyhydroxylated pyrrolidine is easily accessible by Tamao-Fleming oxidation2.
The authors optimized the reaction and found that the outcome critically depends on the substituents on nitrogen and silicon and the choice of Lewis acid. The product molecule 3 has four stereocentres and thus there are 16 stereoisomers. Each of these can be paired up with an enantiomer, so there are eight diastereomers. The following discussion will be limited in the following way: Only the reaction shown above will be discussed, which is the highest-yielding reaction reported in the paper, with a yield of 77% and a dr of >98:2. Furthermore, only the major diastereomer obtained (3) and the one minor diastereomer which I consider as most likely to be formed will be submitted for 13C NMR calculation by the GIAO method. Due to the excellent stereoselectivity of the reaction, no other product was isolated and characterized by the group.
The structures of the two isomers were then drawn in ChemBio3D and optimized by MM2. An input file for the DFT Method DFT=mpw1pw91 calculation was prepared and the basis set was set to 6-31G(d,p). The job was submitted to the SCAN for geometry optimization. The job had approximately seven hours of wall time on the Chem2 Cluster, probably due to the relatively high number of atoms, espcecially silicon and sulfur.
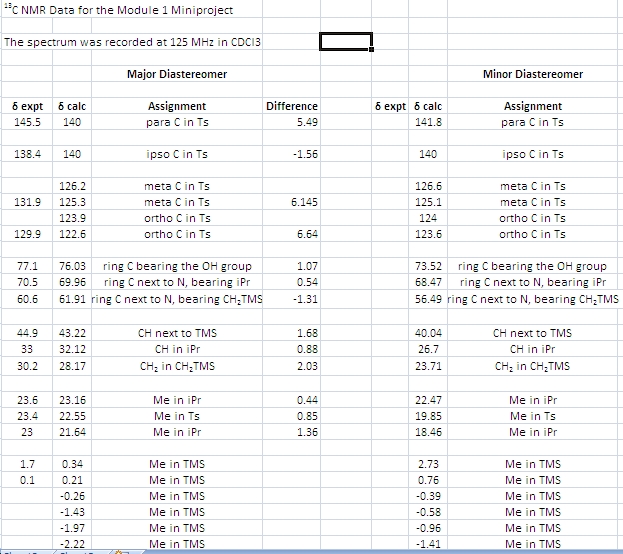
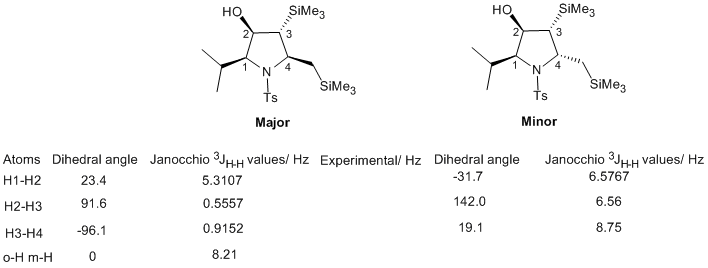
Sure enough, the two predicted 13C spectra differed slightly. However, they do not differ very much, and even if they did, it would be difficult to tell which spectrum belongs to which isomer. IR is unlikely to help since all the functional groups have the same connectivity (i.e. the isomers are not regioisomers). 1H NMR spectroscopy is the most convenient way to distinguish all the potential diastereoisomers that might be formed (there are 4 stereocentres, so there are 16 stereoisomers possible and 8 diastereoisomers). The four ring carbons all bear a hydrogen substituent. By predicting all the 3JH-H coupling constants from the dihedral angles according to the Karplus equation and then comparing them to the recorded spectrum, it should be possible to identify which stereoisomer one has obtained.
Furthermore, since the starting alpha-amino aldehyde is enantiomerically pure, and the reaction highly stereoselective, the isolated major pyrrolidine product will be enantiomerically pure as well. This means computing the optical rotation and comparing the obtained value to the experimentally determined one offers another means of identifying which isomer has been synthesized.
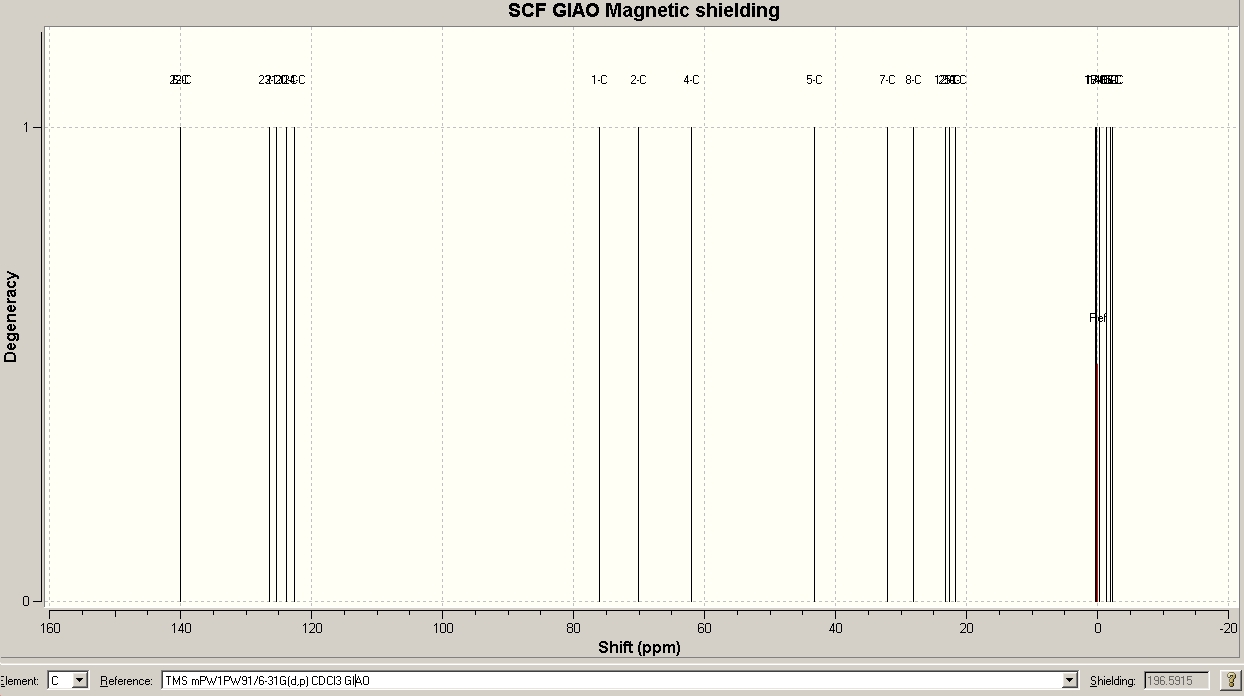
The predicted NMR spectrum for the major isomer is shown above, along with a table (vide infra) comparing predicted and experimental values. The data in the table suggests that the GIAO calculation was successful, because the general agreement of chemical shifts is very good. Only at lower field in the aromatic region deviations of about 5 ppm are observed. At higher field, the deviations are not larger than about 1.5 ppm. There are more signals in the predicted spectrum than in the one which was recorded during the experiment. All of the “extra” signals, however, belong either to aromatic carbons or to methyl carbons that are part of the TMS groups. For instance, the GIAO method predicts both ortho carbons in the Ts group to have different chemical shifts. In the real spectrum, one can only observe one because they are chemically equivalent. Any slight differences in environment between the two ortho carbons are most likely averaged out due to rotations. A similar line of argument applies to the two sets of three methyl groups in the TMS moieties. The programme assigns each group its individual shift, although the three Me groups are chemically equivalent and are thus observed as one signal in the real spectrum. The very good agreement between calculation and experiment can be considered as evidence that the DFT optimized geometry/ conformation is in fact the one adopted by the pyrrolidine 3 in CDCl3 solution!
As a general observation, it is quite remarkable that the predicted spectrum agrees so well with the real one. In particular, without knowing the real spectrum, one could easily assign all the resonances around 0 ppm to the silane methyls (their environment is very similar to that of the standard TMS). Then there is a region of methyl groups at around 20 ppm, the methylenes and methines at 30-40 ppm, followed by the carbons next to heteroatoms (N, O) at 60-80 ppm. Finally, the aromatic carbons come in the region typical for (aromatic) double bonds at 120-140 ppm.
In retrospect, this molecule appears to have been quite a good/ lucky choice with regard to testing the accuracy of the computational method.
The above table shows the dihedral angles and coupling constants in the two isomers as predicted by the Janocchio programme. The column with experimental values is empty, the values from top to bottom (for the major isomer) should read as follows (J couplings from Supporting information of ref. 1): 9.7 Hz, 8.7 Hz, 4.0 Hz.
Clearly, the programme does not reproduce these. It is possible that the silicon substituents make the use of the Karplus equation unreliable. But there are still other methods of distinguishing the isomers. The easiest one of those is of course crystallizing the compounds and subjecting them to x-ray diffraction analysis. This will give relative and absolute stereochemistry. Another way would be to conduct a NOE experiment.
The final part of the discussion will be devoted the question of why such excellent stereoselectivity is observed. For this, it is best to refer back to the first figure in this section on chelation-controlled diastereoselectivity.
There is a hydrogen bond between the NHTs and C=O groups. Nucleophilic attack of the allylsilane on the carbonyl group (activated by the Lewis acid BF3) occurs from the less hindered Si face. This the origin of the syn relationship between the substituents at C1 and C2. The syn-synclinal mode of attack of the alkene means that the future C3 substituent has the orientation shown (pointing down), therefore it is likely to be anti to the substituents at C1 and C2. Finally, the observed anti relationship between the two substituents at C3 and C4 can be traced back to the trans alkene. There is of course a carbocation intermediate with free rotation about the bond, so the fact that virtually only one isomer is observed suggests that trapping of the cation by the nitrogen atom is faster than bond rotation.
In theory, the eight diastereomers may arise from the imperfection of the above mentioned factors that control the selectivity. Nucleophilic attack might occur on a carbonyl group that is not H bonding to the amine. The silane might also attack in another mode. Bond rotation could just as well have been faster or as fast as cyclization, with unpleasant effects on the stereocontrol. The fact that there is still high selectivity, with so much to go wrong, is quite impressive.
References
1. Restorp, P., Fischer, A., Somfai, P., J. Am. Chem. Soc., 2006, 128, 12646-12647, DOI: http://dx.doi.org/10.1021/ja0647102
2. Fleming, I. et al., J. Chem. Soc., Perkin Trans. 1 1995, 317-337