Rep:Mod:cdhxp74297
Part 2: Stereoisomerism in Mo(CO)4(PCl3)2
Last year we conducted a synthesis of cis- and trans-isomers of Mo(CO)4(PPh3)2. We took Molybdenum hexacarbonyl to yield cis-Mo(CO)4(piperidine)2, after refluxing in toluene and excess piperidine. On continued reflux in DCM, with PPh3, a substitution reaction occurred to yield cis-Mo(CO)4(PPh3)2. This underwent thermal isomerisation at 120oC to yield the trans-isomer.
We are going to investigate the structure and vibrational frequencies of related complexes. Due to the computationally intensive nature of the phenyl- groups of the phosphine ligands, they will be replaced with chlorine atoms - this has been shown[1] to be a valid strategy when dealing with bulky phosphines, both in terms of electronic and steric effects.
Stability of Stereoisomers
Optimisation Procedure
Using Gaussview, the two isomers of Mo(CO)4(PCl3)2 were built, initially placing a Mo octahedral fragment, then placing the CO fragment and PH3 fragments into their positions, before substituting the hydrogen atoms for chlorine atoms. These were then optimised, using a low level pseudo-potential basis DFT/B3LYP/LANL2MB calculation, specifying a loose convergence criteria for this initial optimisation.
MoCO4PCl32cis |
MoCO4PCl32trans |
The resulting geometries of these calculations are shown. This level of calculation however, is not sufficient to optimise the conformation of the PCl3 group. Also, the optimisation resulted in PCl3 bond lengths which were longer than the predetermined range encoded into Gaussview, hence the bonds were not shown. Why is this? Gaussview is just an interface. All it gets when it opens up a log file is a set of coordinates and the atomic types at that point (and vibrations data etc). The interface will the calculate the distances between all the atomic pairs, and using a list of allowed bond ranges encoded somewhere into its program, draw bonds for distances within that range. Gaussview was developed for mostly organic molecules, so when we have coordination to a metal centre we know that the bonding behaves very differently to that in an organic fragment, so hence, the value falls outside the specified range. Also, jmol receives .mol files. These define a set of coordinates and the connections, which is created from Gaussview, so whichever connections are determined by Gaussview will also be shown by jmol.
We can define a bond as the constructive overlap of two electron wavefunctions of component atoms resulting in an increase in the probability of finding an electron within the internuclear region. If this increase in electron density is symmetric about an internuclear axis, we call it a sigma bond, if it is symmetric about a plane between the two nuclei, we call it a pi bond.
To correct the PCl3 conformation, we first defined the P-Cl bond lengths as single bonds, to be able to treat the PCl3 group as a group when we then went onto modify the dihedral. Failure to do this would only move one Cl atom, not all three. The dihedral angles of a Cl-P-Mo-C unit were set, so as to fix the conformation of the PCl3 group, relative to the CO ligand cis- to it. In the trans-isomer, the PCl3 ligands were set to line up above each other, and stagger a CO group. In the cis-case, the two PCl3 groups were set to stagger opposite CO groups, so were 180o apart from each other. Then this new geometry was optimised using a LanL2DZ basis set - a much more accurate basis compared to LanL2MB. We also specified an ultrafine convergance criteria. The resulting geometries from this calculation are shown
MoCO4PCl32cis |
MoCO4PCl32trans |
However, this LanL2DZ basis still uses only uses a minimal (s and p) basis set to describe the phosphorous. We need to introduce a larger basis set for phosphorous to allow the calculation to describe its d-AO's. With this extra basis included, the optimisation was repeated, and the geometries shown below were produced.
MoCO4PCl32cis |
MoCO4PCl32trans |
We see the final trans-geometry involves the PCl3 groups staggering each other, and almost totally staggering one CO ligand too. The cis- complex too is staggered off the CO ligand, and also opposite for each ligand, to reduce steric bumping.
We shall carry out an analysis of the frequencies of our final geometries, to ensure once again that we have reached a minimum, stable conformation, using the same calculation: DFT/B3LYP/LanL2DZ freq int=ultrafine scf=conver=9 extrabasis. The cis-conformation has two negative frequencies, of -1.2924cm-1 and -0.0004cm-1. These are close enough to zero that we can be confident in our finding a minimum. The trans-isomer has three negative frequencies, of -2.3449cm-1, -2.0025cm-1 and 0.0008cm-1. Again, these are close enough to zero to trust in the result.
Stability of Isomers
The cis- and trans-isomers of Mo(CO)4(PCl3)2 were optimised, as described above. We are now going to comment on the relative stability of these two isomers, and consider why this may be.
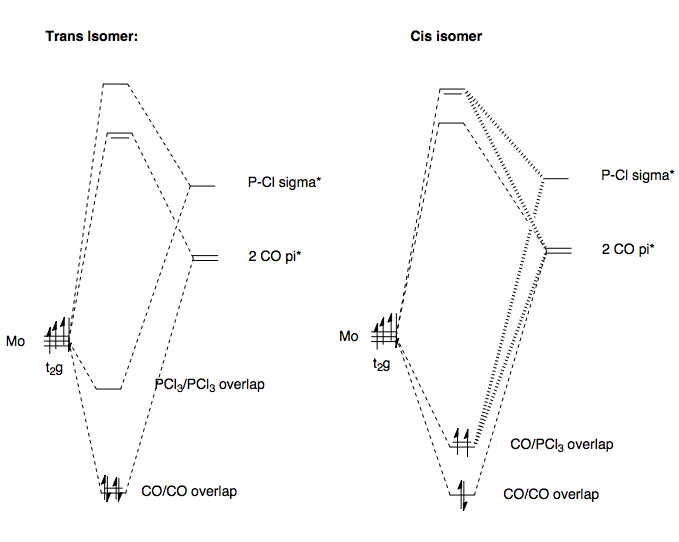
The trans-Mo(CO)4(PCl3)2 complex is 3.27Kjmol-1 more stable than the cis-isomer. Why would this be? We can consider two possible reasons for this: steric and electronic.
The CO ligand is a good π-acceptor, due to the low energy CO π* orbital. The overlap between a Mo d-orbital in the t2g set and the π* orbital of CO will stabilise the complex. The overlap between the P-Cl σ* orbital and Mo d-orbital of the t2g set however, is not as stabilising as the π* overlap, because the σ* is a higher energy acceptor. In the trans-complex, each metal t2g orbital will overlap with a pair of CO liagnds or a pair of PCl3 ligands, trans to each other. The orbitals overlapping with two CO ligands will be highly stabilised relative to the t2g energy level. The orbital overlapping with the PCl3 ligands will be less stabilised. However, Mo is a d4 metal. So, by Hunds rule, we fill the lower, stabilised orbitals first, and overall, the complex is stabilised because the electrons occupy the highly stabilised CO overlap d-orbitals, leaving the PCl3-overlap less stabilised orbitals are left empty.
This is not the case for the cis-complex. Now, for the 3 t2g orbitals, one has a CO/CO overlap, and will stabilise as the trans-isomer did, but now two have two CO/PCl3 overlaps. The PCl3 is less stabilising as we said, so overall, these two orbitals are again less stabilised than the CO/CO overlapped d-orbital, but will be more stabilised than the PCl3/PCl3 overlapped d-orbitals. Now, since only one orbital was highly stabilised by two CO overlaps, this is filled before all d-electrons are accounted for. The next two have to go into a degenerate PCl3/CO-stabilised d orbital, which is higher energy and hence, overall, the cis-complex is higher energy than the trans-.
There is also a steric effect. Placing two bulky PCl3 groups cis- will cause them to sterically bump, or electrostatically repel due to their proximity, and hence raise the energy of the cis- complex. This is not the case for the trans-complex, as the ligands are far removed from each other.
To test this, other complexes of cis- and trans-Mo(CO)4(PX3)2 were optimised, using the same procedure as above, and the energy of the two isomers calculated. When Mo(CO)4(PMe3)2 was studied, the trans isomer was found to be 3.11Kjmol-1 more stable than the cis-isomer. This is slightly less stabilised than the PCl3 complex was. This complex was chosen because the size of the PMe3 and PCl3 ligands are comparable. Then, any difference is due to electronic influences. The measure of phosphine size is based upon the cone angle of the ligand. The cone angle of the PMe3 is 118o, and that of PCl3 124o. The acceptor P-C σ* orbital is a higher energy acceptor than the Cl-P σ*, so hence, the stabilisation by overlap is less good, and hence the trans-isomer is less stabilised compared to the cis- than when PCl3 ligands were used.
trans-Mo(CO)4(PH3)2 low frequencies: -6.3477cm-1 -6.1131cm-1 -0.0005cm-1 -0.0002cm-1
cis-Mo(CO)4(PH3)2 low frequencies: -0.0010cm-1 -0.0007cm-1 -0.0006cm-1
The complexes cis- and trans- Mo(CO)4(P(OH)3)2 were also studied. These complexes may be impossible to form, a metal-phosphoric acid type species, but they are here to demonstrate a point, which could be applicable to phosphonate species. In this complex, the trans isomer is now 36.16Kjmol-1 less stable than the cis-isomer. The trend has been reversed, despite the fact that the P-O σ* is a good acceptor, and we would expect stabilities comparable tot the PCl3 complexes. However, now there is an additional factor to consider. In the cis- isomer, the POH3 ligands are twisted so as to allow a hydrogen bond to operate between them. This extra stabilising interaction overcomes the observed trend and the cis- is stabilised over trans-.
trans-Mo(CO)4(P(OH)3)2 low frequencies: -0.009cm-1 -0.0008cm-1
cis-Mo(CO)4(P(OH)3)2 low frequencies: -4.4271cm-1 -1.3260cm-1 -0.0004cm-1
Vibrational Modes of CO ligand stretching
Vibrational modes of M(CO)4(L)2, where L is a point ligand

To understand the vibrational spectra of the two isomers of Mo(CO)4(PCl3)2, I shall present here the derivation of the vibrational modes of the CO stretching frequencies in octahedral complexes from first principles.
To begin with, we shall consider the ideal stereoisomers of M(CO)4(L)2 where L is a point ligand, so having the highest possible symmetry. The trans isomer is of the point group D4h. The cis-isomer is of the point group C2v.
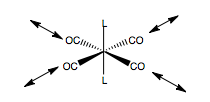
We can place displacement vectors along the carbonyl groups to represent the stretching modes of the ligands. A double headed arrow represents this stretch. This is our basis set to determine the form of the symmetry allowed carbonyl stretching modes. Then we form the reducible representation of this basis, by seeing how the displacement vectors individually transform under the operations of the point group. For each vector that is unchanged by an operation, we count 1 for the representation. For each that is reversed in direction, count -1, and for those which move, count 0.
For example, under operation E of the D4h point group, all vectors remain unchanged, so we count 4 as the character of the reducible representation for this basis set. Note that to determine the vibrational modes of the molecule in total, we would need to place x,y,and z displacement vectors on each atom, to allow all atoms to move independently, then find the irreducible representation of that basis set. However, we are only interested in the carbonyl stretching modes, so we can use this reduced basis. Under the operations 2C4, all 4 displacement vectors rotate by 90o. Although they map onto each other, we are looking at the individual vectors when determining the reducible representation, and they all moved, so we count 0 as the character of the operation for this basis. Repeating this for all the operations of the D4h point group, we obtain the reducible representation for this CO stretching basis set. This is shown, left.
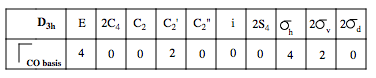
Now, we need to break this reducible representation up into its irreducible components. Think of the analogy of a jigsaw puzzle. We find a complete jigsaw, but if we are to know how many pieces it has, we need to break it up and count. We apply the reduction formula to our reducible representation. This tell us, for a given irreducible representation of the D4h point group, how many times it is a component of our reducible representation.
Where h is the number of operations of the point group, k is the number of symmetry operations of a type, chiR is the character of the reducible representation for that symmetry operation, and chiIR is the character of the irreducible representation of the symmetry operation. Summed over all operations of a group.
For the A1g irreducible representation, we shall go through the sequence.
n(A1g) = (4x1x1) + 0 + 0 + (2x2x1) + 0 + 0 + 0 + (1x4x1) + (2x2x1) = 4 + 4 + 4 + 4 = 16/16 = 1. Hence, there is one A1g irreducible representation as a component of our reducible representation.
We do the same for all other irreducible representations of the point group, and obtain the sum of the irreducible representations that make up our reducible representation: ![]()
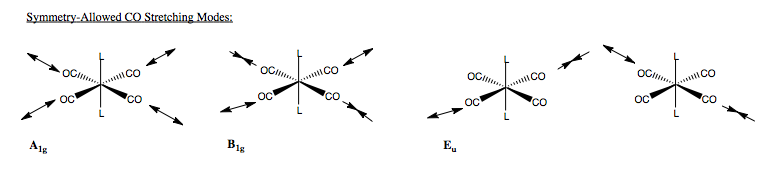
This tells us that the carbonyl stretching vibrations have four symmetry allowed modes - two non degenerate and one double degenerate. This is only half the problem though. We still have yet to determine what the vibrations look like. Only then can we determine whether or not we will see them on an IR spectrum of this compound. One component of the reducible representation is an A1g mode. This corresponds to a totally symmetric stretch across all four CO groups. To determine the form of other vibrations, we form guesses of the vibrations, then take the vectors which will represent that vibration, and determine their symmetry under the D4h point group. In complex molecules we would have to use the projection operator to determine vibrations, but here again we are just looking at CO stretching, so can get away with educated guesses.
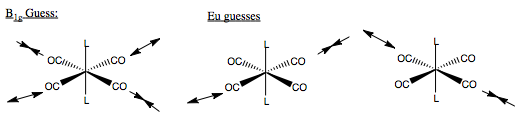
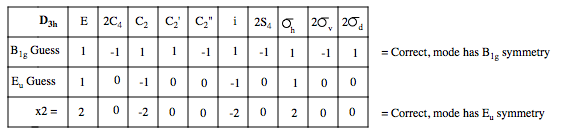
We have a non-degenerate mode, and a doubly degenerate. The non-degenerate mode must correspond to a vibration in which the displacement vectors do map onto each other - therefore, we can say that in this mode, all four groups are vibrating, but not symmetrically, otherwise it would be of A1g symmetry. Using the same thinking, we can say that the doubly degenerate mode, only two CO groups are vibrating, also this is a gerade mode, so each vector will have the opposite phase. Hence, we form our guesses. We see how these act under the symmetry operations of D4h, for the non-degenerate mode, we simple see how the phase changes, for the degenerate mode, we see if the phase changes and if the vectors do not map on to each other, and find that these guesses do have the symmetry.
Finally, we need to determine whether the modes are IR active. The selection rule for and optically active vibrational mode is that the dipole moment of the vibration must change on transition. Looking at the A1g and B1g displacement vectors, we see they are symmetric across the metal centre. Hence, there is no change in dipole, and these two modes are IR inactive. The Eu modes on the other hand are non-symmetric across the M centre, so a dipole change occurs on vibration, and hence the modes are active. In this spectrum, we would expect to see only one peak for the CO stretching modes, made up of two degenerate stretching modes of opposite CO groups.
Since in this section we are looking at Molybdenum stereoisomers, it made sense to test this prediction by calculating the vibrational modes of the Mo(CO)4(Cl)2. However, the molecular geometry is found to be D2h, not D4h, as expected for such a complex. We see a Jahn Teller distortion for this molecule, resulting in the two sets of trans CO ligands having different lengths. The complex is likley a low spin complex, due to the large ΔO from the strong CO ligands, hence the d4 complex has an unevenly occupied t2g set, and thus, a weak distortion. The optimisation was repeated for Nb CO4 Cl2, which is a d3 complex, hence should show no JT distortion, but once again, a D2h symmetry resulted, this time though with a smaller distortion. This does not make sense in CFT. If we treat the molecule under the MO theory instead though, the D4h geometry may not be as stable as the D2h geometry, and by distortion, may result in removal of t2g degeneracy, and lowering of energy, by better orbital overlap, for example.
MoCO4PCl32trans |
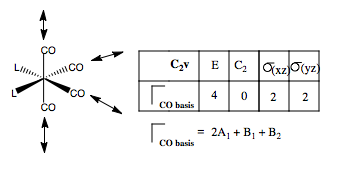
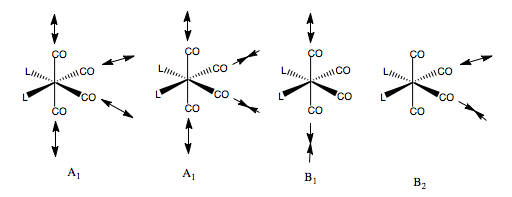
Now, doing the same for the cis-C2v Geometry. Once again, we form our basis by placing stretching vectors on the CO groups, and find the reducible representation of this basis. Then we use the reduction formula to find the component irreducible representations of the C2v point group. The CO groups have four, non-degenerate stretching modes.
What are the form of these modes? Once again, we can guess that one A1 mode must be totally symmetric across the whole molecule. Also, looking at the point group, if a vibration is symmetric for both types of CO ligand, i.e the same across the xz plane and the same across the yz plane, then the symmetry will also be A1. Hence, we can form a guess where each of the pairs of like-CO ligands are moving in the same way, but the pairs vibrate out of phase. The B1 mode must reverse direction on reflection in the yz plane, hence the cis-CO ligands must have opposite phase. Likewise for the B2 mode, the vibration reverses in the xz, so the trans-CO ligands must reverse phase. Here are our guesses.
All these modes should be IR active, since the CO ligands are unequally distributed about the metal centre, so any CO vibration will result in a change in the dipole moment.
We can test this prediction against a real molecule. Optimising the geometry of cis-Nb(CO)4Cl2, initially using a loose DFT/B3LYP/LanL2MB type calculation, then a more rigourous tight DFT/B3LYP/LANL2DZ, the geometry was optimised, and the vibrations calculated. The resulting calculated stretching CO modes are shown here. Our predictions match the calculated
|
Comparison between predicted and calculated CO stretching modes in Nb(CO)4(Cl)2 |
||||||||
|
Symmetry |
Prediction |
Calculation |
||||||
|
Mode |
Active |
Mode |
Frequency /cm-1 |
Intensity |
||||
|
A1 |
IR active |
|
2041 |
133 |
||||
|
A1 |
IR active |
|
1966 |
787 |
||||
|
B1 |
IR active |
|
1962 |
1806 |
||||
|
B2 |
IR active |
|
1958 |
465 |
||||
Vibrational modes of isomers of Mo(CO)4(PCl3)2: The effect of removal of symmetry of the vibrational spectra
Now, we discuss the effect of replacing point ligands for groups, and look at cis- and trans-isomers of Mo(CO)4(PCl3)2. The trans isomer is in the Cs point group, as the PCl3 groups stagger each other, so the only symmetry element this molecule has is a mirror plane in the Mo(CO)4 plane. The point ligand molecule was ideally D4h, but we found it to commonly be D2h due to a JT type distortion. The D4h point group had a pair of degenerate CO stretching modes. The Cs point group has no degenerate irreducible representations. Let us once again form our CO stretching basis, to determine the reducible representation, then use the reduction formula to determine the component IR's. In this case, it is almost trivial.

What is the form of these four CO streetlight modes? Since the CO ligands lie in the mirror plane, any possible combination of the CO stretches will be of A' symmetry. However, we can use the results from above to suggest possible modes. We expect a totally symmetric CO mode, with all 4 ligands in phase. This would likely be IR inactive, as the dipole moment would not change because all four move in phase. We might also expect a mode where trans-pairs of CO ligands are in out of phase with each other, as was the B1g set of the trans-M(CO)4L2compex above. This again would be IR inactive. Finally, two modes where only one pair of trans ligands vibrate, out of phase with one another. These two will be IR active, because of the unequal CO vibration across the metal centre. These are technically non-degenerate, because of their symmetry, but we would expect them to vibrate at very similar energies and intensities because of the same form of the displacement. Our guesses:

And those calculated:
|
Comparison between predicted and calculated CO stretching modes in Mo(CO)4(PCl3)2 |
||||||||
|
Symmetry |
Prediction |
Calculation |
||||||
|
Mode |
Active |
Mode |
Frequency /cm-1 |
Intensity |
||||
|
A' |
IR inactive |
|
2026 |
5.4 |
||||
|
A' |
IR inactive |
|
1967 |
5.8 |
||||
|
A' |
IR active |
|
1940 |
1606 |
||||
|
A' |
IR active |
|
1939 |
1607 |
||||
Our prediction is good, with the form of the modes corresponding well. We predicted that the two modes where all four ligands vibrate to be IR inactive, because the dipole moment of the complex is unchanged, but we see a very weak signal in the calculated spectrum. Possibly the displacement of the CO ligand into the Cl charge cloud might upset the dipole moment very slightly, causing a formally forbidden transition to be very weakly allowed.
Cis-Isomer. The effect of replacing the cis-point ligands with PCl3 groups, is to reduce the symmetry from C2v to C1, i.e no symmetry beyond the identity, because the PCl3 groups are staggered differently, otherwise two Cl atoms would bump, and this would be high energy. Hence, forming a CO basis with 4 stretching vectors instantly leads us to realise that we have four CO type stretching modes, all of A symmetry - the only possible option. Any possible combination of displacement, phase and number of the CO ligands moving would fit this representation, so guessing would not be valid. If we compare to cis-Nb(CO)4(Cl)2 modes above. The removal of symmetry however, will probably mean the vibration is not as 'clean'. Before, in the C2v molecule, the symmetry fixed the vibrations to given ligands. Now though, as we have said, any vibration is symmetry allowed. Hence the displacement might not be confined to one particular ligand/set of ligands. We can however, predict that all vibrations are IR active, since the dipole moment would change with any CO movement because the CO ligands are distributed unevenly around the metal centre.
If we animate the vibrations, we see that two, involving the 4 ligands are of comparable form to the C2v vibrations. However, the other two are messy, as expected. In the C2v molecule, these vibrations involve one one pair of ligands. Now, the vibration is mostly associated with one pair, but we see slight movement in the other pair. All are optically active, as expected.
|
Calculated C1 cis-Mo(CO)4(PCl3)2 vibrational modes. |
|||||
|
Mode |
Frequency /cm-1 |
Intensity |
|||
|
2020 |
541 |
|||
|
1953 |
593 |
|||
|
1942 |
823 |
|||
|
1939 |
1595 |
|||
Files
Trans-Mo(CO)4(PCl3)2 DFT/B3LYP/LanL2DZ Extra P basis Optimisation: [1]
Trans-Mo(CO)4(PCl3)2 DFT/B3LYP/LanL2DZ Extra P basis Frequency: [2]
Cis-Mo(CO)4(PCl3)2 DFT/B3LYP/LanL2DZ Extra P basis Optimisation: [3]
Cis-Mo(CO)4(PCl3)2 DFT/B3LYP/LanL2DZ Extra P basis Frequency: [4]
Trans-Mo(CO)4(PH3)2 DFT/B3LYP/LanL2DZ Extra P basis Optimisation: [5]
Trans-Mo(CO)4(PH3)2 DFT/B3LYP/LanL2DZ Extra P basis Frequency: [6]
Cis-Mo(CO)4(PH3)2 DFT/B3LYP/LanL2DZ Extra P basis Optimisation: [7]
Cis-Mo(CO)4(PH3)2 DFT/B3LYP/LanL2DZ Extra P basis Frequency: [8]
Trans-Mo(CO)4(P(OH)3)2 DFT/B3LYP/LanL2DZ Extra P basis Optimisation: [9]
Trans-Mo(CO)4(P(OH)3)2 DFT/B3LYP/LanL2DZ Extra P basis Frequency: [10]
Cis-Mo(CO)4(P(OH)3)2 DFT/B3LYP/LanL2DZ Extra P basis Optimisation: [11]
Cis-Mo(CO)4(P(OH)3)2 DFT/B3LYP/LanL2DZ Extra P basis Frequency: [12]
Trans-Mo(CO)4Cl2 DFT/B3LYP/LanL2DZ Optimisation: [13]
Trans-Mo(CO)4Cl2 DFT/B3LYP/LanL2DZ Frequency: [14]
Cis-Nb(CO)4Cl2 DFT/B3LYP/LanL2DZ Optimisation: [15]
Cis-Nb(CO)4Cl2 DFT/B3LYP/LanL2DZ Frequency: [16]
General references made throughout to:
T.Hunt, Molecular Orbitals in Inorganic Chemistry Lecture Course, 2009-2010
K.C.Molloy, Group Theory For Chemists, 2007
J.B.Foresman and A.Frisch, Exploring Chemistry with Electronic Structure Methods, 1996
Part 1: Introduction to the Course: BH3 and TlBr3