Rep:Mod:ccmodule3
Introduction
The Cope rearragement is a highly useful synthetic rearrangement involving the thermal isomerism of 1,5 dienes. It is an example of a pericyclic [3,3] sigmatropic reaction and can either go through a boat or a chair transition state. In this report, the simplest 1,5 diene, 1,5 hexadiene will be used to investigate this reaction through location of the low-energy minimum and transition structures on the C6H10 potential energy surface, to determine the preferred reaction mechanism. Though study of this reaction is complicated by the fact that the reactant and the product are the same molecule, analysis of the conformers of 1,5 hexadiene allows us to predict the path of the reaction.
Conformers of 1,5 hexadiene
Optimising the Reactants and Products
1,5 hexadiene has 27 possible conformational minima, however only 10 are energetically distinct. A selection of these 10 will be investigated and the symmetry of the conformers, the vibrational frequencies and the potential energies will be compared and contrasted with an intention to explaining the reaction. Firstly a molecule with an anti linkage for the central 4 atoms will be drawn by setting the dihedral angle to 180°. It would be expected that this would generate a low energy conformer due to the reduced steric interactions. In total 4 anti conformers and 2 gauche conformers were generated and a summary of the results is given below. The structures were first built using the Gaussian builder and then the structures were cleaned using the "clean" function.All results were generated using the HF/3-21G level of theory.
| Conformer | Structure | Point Group |
Energy/ (Hartree) HF/3-21G |
Relative Energy / (kcal/mol) | |||
| gauche3 |
|
C1 | -231.61132932 | 0.00 | |||
| gauche5 |
|
C1 | -231.68961573 | 0.62 | |||
| anti1 |
|
C2 | -231.69260213 | 0.04 | |||
| anti2 |
|
Ci | -231.69253530 | 0.08 | |||
| anti3 |
|
C2h | -231.68907000 | 2.25 | |||
| anti4 |
|
C1 | -231.69097055 | 1.06 |
The results agree well with the values and geometries given in Appendix 1. The first conformer produced had a C2 symmetry and was deemed to be the anti1 confromer. As expected, it is a low energy conformer; the steric interactions are minimised due to the large distance between the neighbouring hydrogen atoms. A gauche conformer was then produced which had C1 symmetry. It was expected that this conformer would have a higher energy than the anti 1 conformer, due to increased steric strain imposed by the more constrained geometry. This was indeed the case with this confomer having an energy of 0.0029864 hatree higher than the anti 1 conformer. Bearing these 2 examples in mind, it would be expected that the lowest energy conformer would be one that minimised steric interactions hence the other anti conformers were analysed. The results show that in fact, the anti 1 conformer is the lowest energy conformer within the anti subgroup as steric interactions between vicinal hydrogen increase the energy of the other conformers. The gauche conformers were then analysed with the gauche 3 conformer first generated. This conformer was found to be the lowest energy conformer, due to the stabilising effect of donation from the σ C-H orbial into the π* C=C orbital. In this conformer, the largest number of these interactions can be found leading to the lower energy.
The anti 2 conformer generated earlier was optimised a second time at a higher level of theory (B3LYP/6-31G*). A comparison of the structures is given below.
| Property | (HF/3-21G) | (B3LYP/6-31G*) |
|---|---|---|
| Dihedral Angle (o): C1-C2-C3-C4 | 114.64446 | 116.34946 |
| Dihedral Angle (o): C6-C5-C4-C3 | -114.64446 | -116.34946 |
| Dihedral Angle (o): C5-C4-C3-C2 | 180.0000 | 180.0000 |
| Bond length (Å): C1=C2 | 1.31615 | 1.31615 |
| Bond Length (Å): C2-C3 | 1.50888 | 1.50890 |
| Bond Length (Å): C3-C4 | 1.55288 | 1.50888 |
As can be seen there is very little difference between the structures generated using the different levels of theory. The HF/3-21G method provides slightly smaller dihedral angles and longer bond lengths bond lengths meaning this optimised structure will be slightly longer. However this difference is less than 0.1Å therefore it is unlikely that the properties and reactivity of the molecule will be affected.
The energy difference between the Anti 1 and Gauche 3 conformers is very low so the structures were reoptimised at the same higher level of theory as for the Anti 2. The energy for the Anti 1 conformer at the B3LYP/6-31G* level was -234.61178344 and the energy for the Gauche 3 conformer was -234.61132932 therefore the Gauche 3 confromer is still the more stable. Clearly at this higher level of theory, the reduced steric interactions in the Anti 1 conformer are still dominated by the stereoelectronic stabilising interactions in the Gauche 3 conformer. Higher level calculations by B. G. Rocque et al. show that in fact Anti 1 is the lowest energy conformation. This is surprising but not entirely unexpected; the energy difference between the σ C-H orbial and the π* C=C orbital is fairly large so the stabilising interactions will be correspondingly small.
Vibrational Analysis
To confirm a minimum had been found a frequency calculation was performed on the Anti 1 conformation using the B3LYP/6-31G* level of theory. A snippet of the log file is reproduced below:
Low frequencies --- 74.1930 99.5011 109.1601
Diagonal vibrational polarizability:
2.9049660 1.7787969 1.7061022
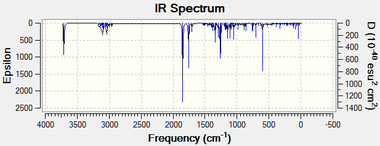
As can be seen, there are no negative frequencies; these would indicate a transition state. This is because negative frequencies mean a minimum has not been reached on the potential energy surface. The IR spectrum is reproduced below.
The high symmetry of this molecule is reflected in its IR spectrum. Though there are 42 vibrational modes only about 10 have a large amplitude. It is likely the overall dipole change is retarded in stretches due to the high symmetry leading to many absorptions which will almost certainly blend into the background noise experimentally.The lack of negative frequencies is further illustrated in this IR; as can be seen all absorptions are "real". Vibrational analysis can also give thermochemistry data and this is given below.
Sum of electronic and zero-point Energies= -234.469318 Sum of electronic and thermal Energies= -234.461978 Sum of electronic and thermal Enthalpies= -234.461034 Sum of electronic and thermal Free Energies= -234.500253
The values produced correspond to thermochemical quantaties calculated by Gaussian through analysis of the various partition functions. The calculation was attempted at 0K but the computer did not work under these conditions. It would be expected that the various energies would all converge to a single value smaller than any values above. This is beacause at 0K the only contribution to the above values will be the electronic and zero point energies as the rotational and vibrational partition functions are both temperature dependent and so their values will be 0 at 0K.
http://pdfserve.informaworld.com/309877_910068705_713826977.pdf
Optimising the chair and boat transition structures
The Cope rearragement can go through either a chair or a boat transition state, however the boat transition state is known to be several kcal/mol higher in energy so is unfavoured. Using different methods of transition state optimisation these differences will now be rationalised and properties such as the point groups, etc. will be reported.
An allyl fragment was first optimised using the HF/3-21G level of theory and then copied and pasted twice into a new molecule window. The 2 allyl fragments were then positioned to form an initial guess for the transition state; the terminal ends of the 2 fragments were placed 2.2Å away from each other. This initial structure was optimised to a transiton state by changing the job type to Opt+Freq and the method was changed to Optimization to a TS (Berny). The additional keywords "Opt=Noeigen" was added to ensure the calculation did not fail if multiple negative frequencies were found. The structure generated is given below.
Vibrationjwp108 |
This structure has the following physical properties.
-Energy: -231.61932247 hartree -Point group: C2h -Distance between terminal ends: 2.02 Å
The results for the allyl fragment is given below.
-Energy: -115.81025009 hartree -Point group: C2v
The difference between 2 x allyl fragments and the transition state is -0.00117771 hartree which equates to -3.09148875kcal/mol. This means the 2 allyl fragments are more stable than the transition state corresponding to the idea that the transition state is more unstable than the reactants and could potentially be at a potential energy maximum. To test whether the system is at a maximum, a vibrational analysis was performed on the system. The frequency data is reproduced below.
Low frequencies --- -817.9502 -3.0116 -2.0401 -0.0005 -0.0002 -0.0002
Low frequencies --- 1.7607 209.5561 396.1026
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
8.0501323 2.5576696 0.4527939
Diagonal vibrational hyperpolarizability:
0.0076589 0.0365747 -0.0022332
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -817.9502 209.5561 396.1026
Red. masses -- 9.8858 2.2189 6.7662
Frc consts -- 3.8969 0.0574 0.6255
IR Inten -- 5.8668 1.5762 0.0000
Raman Activ -- 0.0001 0.0000 16.9000
Depolar (P) -- 0.2696 0.7497 0.3845
Depolar (U) -- 0.4247 0.8569 0.5554
As can be seen there is only 1 negative frequency of a significant magnitude at -817.9502cm-1. Multiple large negative vibrations would be indicative of a failed calculation as it means there are multiple ways for the system to become more stable. This negative frequency is animated below.
| Negative Vibration |
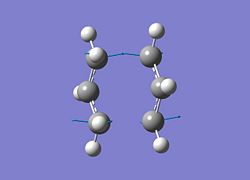 |
This vibration corresponds directly to the bond breaking/bond making process of the Cope rearrangement in hexadiene with concerted bond breaking and bond making concerted as would be expected for a pericyclic reaction.
Frozen cooordinate method
The frozen coordinate method is an alternative to finding the transition state of a reaction. In this method the geometrical parameters of the reacting centres are frozen and the rest of the molecule is optimised. Following this optimisation, the distance between the reacting terminal atoms is optimised. This method is preferred to the previous method for a combination of reasons. A bad guess for the transition state will fail with the earlier method as the curvature of the potential energy surface will be far away from the transtion state potential energy surface. Furthermore if the transition state optimisation is computationally expensive, breaking the problem into 2 parts means that even if the final optimisation does not compute successfully, we are still left with a partially optimised molecule.
The final results are given below.
Vibrationjwp108 |
As can be seen from the above structure produced appears very similar to the structure produced using the earlier method. The distance between the terminal hydrogens is 2.02Å; the same as for the earlier optmisation. A vibrational analysis was performed to see whether this structure is a true transition state. A portion of the log file is reproduced below.
Low frequencies --- -817.9565 -5.0179 -0.0007 -0.0005 -0.0005 4.5190
Low frequencies --- 6.7959 209.4565 395.6473
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
8.0324157 2.5529117 0.4526389
Diagonal vibrational hyperpolarizability:
0.0132805 -0.0495698 0.0015732
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -817.9565 209.4565 395.6473
Red. masses -- 9.8793 2.2191 6.7601
Frc consts -- 3.8944 0.0574 0.6235
IR Inten -- 5.8514 1.5688 0.0000
Raman Activ -- 0.0003 0.0000 16.9075
Depolar (P) -- 0.2870 0.6240 0.3819
Depolar (U) -- 0.4459 0.7684 0.5527
As can be seen there is only 1 negative frequency with a large magnitude at -817.9565cm-1 . This corresponds almost exactly to the negative frequency generated by the previous optimisation of -817.9502cm-1, implying the 2 transition structures are very similar. The energy of this transiton state was calculated to be -231.61932229 hartree, therefore the difference in energies is -0.00000018 hartree or -0.0004725 kj/mol. This is a very small amount and can be ascribed to the different method of calculation. It can therefore be said with a large degree of certainty that both methods have converged on the same structure.
Boat Structure
As mentioned above, the boat transition state has a higher energy, therefore it is generally unfavoured. Investigation of this transition state requires the use of an alternative method of calculation, the QST2 method. In this method, the products and reactants are specified and the transition state is interpolated from these 2 structures. The reactants and products are the same molecule for this reaction therefore, the atoms must be numbered to allow Gaussian to calculate which atoms are moving where.
The anti 2 conformation was used for this analysis and the results of the renumbering are shown below.
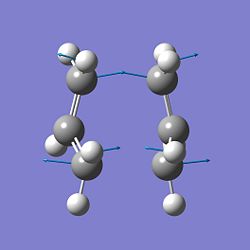
This optimisation failed due to Gaussian's inability to rotate about the single bonds. The structure generated involved 2 overlapping sigma bonds joining the terminal ends. Therefore, the initial structures were rotated; the dihedral angle was set to 0o, and the C2-C3-C4 and C3-C4-C5 angles to 100o. Upon tweaking of the method, the calculation was successful and a boat transition state was made. One imaginary vibration was recorded at -840.9cm-1, this corresponds to the below imaginary vibration.
IRC analysis
Though the mechanism of the reaction has been investigated, the conformation of the final products cannot yet be predicted. An IRC analysis allows us to calculate the energy of the final product and we can correlate that with the energies of the conformers. The energies should match up exactly. An IRC analysis was performed on the chair transition state. Initially it was run with number of points computed as 50 and the the force constant only calculated once.
The following graphs were produced.
| IRC analysis |
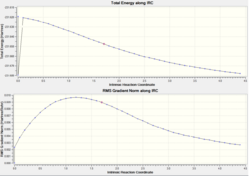 |
As can be seen from the graph, the results have not converged. The RMS value is 0.00895161; well above the 0.0001 normally regarded as a successful reaction. The calculation was repeated with force constants calculated always. The RMS gradient was reduced to 0.00097520 and the following graphs were produced.
| IRC analysis |
 |
This calculation was more successful than the previous one with an energy of -231.68718911 hartree reported for the final structure. This energy corresponds roughly to the energy of the Gauche 1 conformer and by analysis of the structure there is a clear resembalance.
| IRC analysis |
 |
It is unusual that the highest energy conformation is produced so to confirm that this is the correct conformer produced, the structure produced was further optimised to a minimum using the HF/3-21G method. Upon optimisation, the energy decreased to -231.69166698 hartree which correspond well to the Gauche 2 conformer as it is the same to 5 d.p. Furthermore the symmetry corresponded with the conformer produced having C2 symmetry. The conformer is shown below.
| IRC analysis |
 |
Activation energies
The activation energies for the reactions can be calculated by comparing the stability of the reactants to the stability of the transition state. To do this, a higher level of theory is required to ensure good results so the structures were reoptimised at the B3LYP/6-31G* level. The reactant used will be the Anti2 conformer. The results are shown below.
| ' | Chair (HF) | Chair (DFT) | Boat (HF) | Boat (DFT) | Anti2 Conformer (HF) | Anti2 Conformer (DFT) |
| Total Energy (hartee) | -231.6193225 | -234.556983 | -231.602804 | -234.5430931 | -231.6925353 | -234.61171 |
| Sum of Electronic and zero Point energies (hartree) | -231.466699 | -234.414919 | -231.450921 | -234.4023392 | -234.469318 | -234.469203 |
| Sum of Electronic and thermal energies (hartree) | 231.46134 | -234.4089412 | -231.4456 | -234.3960487 | -234.461978 | 234.461856 |
| Activation Energy (kcal/mol) (0K) | 45.94 | 34.34 | 56.31 | 43.06 | N/A | N/A |
Upon comparisson with the appendix it can be seen that the results are in good agreement with experimental values. The boat conformation always has a higher activation energy so the reaction is likely to proceed along the chair transition state path at 0K. The HF method overestimated the activation energy in both cases. Therefore, either the stability of the reactants is underestimated and the stability of the transition state is overestimated or both. This is likely to be because of the relatively poor modelling of the complex electronic structure of the transition state.
The Diels Alder Cycloaddition
The reaction between cis-butadiene and ethene
The Diels Alder cycloaddition is a highly useful synthetic pericyclic reaction between a conjugated diene and a dienophile. The reaction between cis-butadiene and ethene is an excellent example of the reaction. In this case, the 2 molecules react together to form cyclohexene. The reaction is extremely regio and sterospecific with the reaction only taking place if the conformation of the diene is cis and there is potential for overlap between the HOMO and LUMO of the respective ractants.
For there to be significant overlap, the symmetries of the 2 reacting orbitals must be the same with respect to the σv plane of symmetry. Orbitals can either be symmetric or antisymmetric. Therefore the HOMOs and LUMOs of ethene and butadiene will be generated and analysed with respect to symmetry to see whether this criterea is satisfied. The first calculations will be carried out using the Semi Emperical AM1 level of theory.
| Reactant | Molecular Orbital | Symmetry | Energy (a.u) | ||
|---|---|---|---|---|---|
| cis-Butadiene | LUMO | 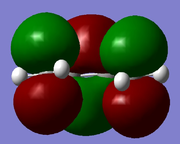 |
Symmetric | -0.207 | |
| HOMO |  |
Anti-symmetric | -0.358 | ||
| Ethene | LUMO |  |
Anti-symmetric | -0.162 | |
| HOMO |  |
Symmetric | -0.395 | ||
As can be seen the HOMOs and LUMOs can interact as they have the same symmetry, therefore a reaction is allowed. A further observation can be made; the energies of the interacting orbitals are relatively similar. According to pertubation theory the amount of stabilisation derived from orbital mixing is inversely proportional to the difference in energy between the two orbitals; the smaller the difference, the greater the stabilisation. Therefore the level of stabilisation is likely to be large for this reaction so the reaction is more likely to be favoured.
The calculations were then repeated at the higher B3LYP/6-31G* level of theory. The orbitals etc. derived are given below.
| Reactant | Molecular Orbital | Symmetry | Energy (a.u) | ||
|---|---|---|---|---|---|
| cis-Butadiene | LUMO |  |
Symmetric | -0.202 | |
| HOMO | 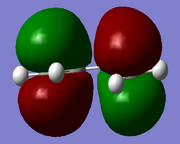 |
Anti-symmetric | -0.362 | ||
| Ethene | LUMO |  |
Anti-symmetric | -0.018 | |
| HOMO |  |
Symmetric | -0.266 | ||
As can be seen the trends in results, i.eusing the AM1 level of theory do not change after use of the higher level of theory. The numerical values for the energy of the orbitals changes but this is due to variation in the method used.
These optimised fragments will then be used to generate the transition state at both levels of theory to allow a degree of comparison. The 2 fragments were placed approximately 2.2Å apart with the guessed transition structure resembling the envelope shape that the transiton state is known to resembled.
| Envolope |
 |
The results for the AM1 and B3LY levels of theory are given below:
| Method | Semi-empricial/AM1 | DFT-B3LYP/631G(d) |
|---|---|---|
| Optimised TS | ||
| Energy/ au | 0.11162917 | -234.54389655 |
| Terminal carbon distance/Å | 2.12 | 2.27 |
| Angle of attack /O | 99.3 | 102.3 |
| Imaginary frequency /cm-1 | -955.502 | -525 |
The transition states have a similar geometry. In especial agreement is the angle of attack which is approximately the same. The distance between terminal carbon atoms increases upon use of the higher level of theory by 0.15Å. This is indicative of the better basis set used. However, in both cases the distance is smaller than the sum of the Van der Waals radii of the 2 Carbon atoms (3.4Å), implying there is a bonding interaction between these 2 carbon atoms. Furthermore there is a contraction in the C-C single bonds and lengthening of the C=C double bonds compared to reference values. The length of the C=C bond is 1.38296Å in the B3LYP transition state compared to 1.3392 Å in the optimised structure for butadiene. Similarly, the bond lengths for the single bond in the transition state is 1.3975Å compared to 1.4702Å in the butadiene reactant using the B3LYP level of theory. This implies that there is a decrease in the bond order caused by a shift in electron density from the double bonds to the single bond and also electron density is increasing in between the terminal hydrogens. In essense, the single bond is turning into a double bond and the double bonds are turning into single bonds. Similar results were acheived when analysing the Am1 results.
In general the AM1 bond lengths were all longer than the B3LYP bond lengths. This shortening reflects increased accuracy with the bond lengths correlating better with the reference values of 1.34Å for the C=C bonds and 1.487Å for the C-C bonds.
The HOMOs for the transition state under both levels of theory are given below.
| AM1 | B3LYP |
|---|---|
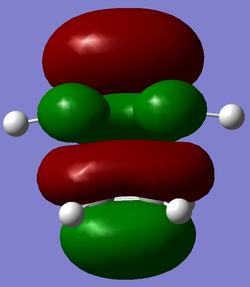 |
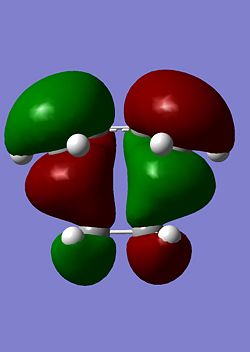 |
As can be seen the HOMO is clearly formed from a combination of HOMO of cis-butadiene and the LUMO of ethene. The B3LYP HOMO is antisymmetric whilst the AM1 HOMO is symmetric. This is a surprising result as both would be expected to be antisymmetric. However, the HOMO-1 is of a very similar energy (-0.355 compared to -0.356) and is antisymmetric. The low accuracy of this method may mean that the ordering of these orbitals is not perfect so it will be assumed that the HOMO-1 is the actual HOMO. This orbital is reproduced below and can be clearly seen to be antisymmetric.
| HOMO-1 |
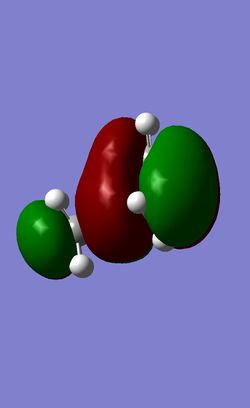 |
The LUMO's for the transition states under both levels of theory are reproduced below.
| AM1 | B3LYP |
|---|---|
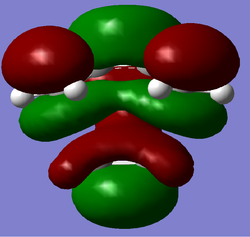 |
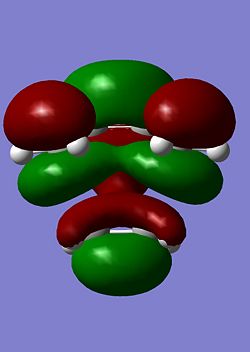 |
Both LUMOs are symmetric as expected and appear to be combinations of the cis-butadiene LUMO and the HOMO of ethylene.
The frequency analysis of both transition states showed one negative frequency. The log file for the AM1 optimised TS is reproduced below.
Low frequencies --- -955.5025 -6.2807 -5.8982 -2.4531 0.0238 0.0812
Low frequencies --- 0.6854 146.9404 246.7240
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
2.3319768 1.4113343 1.2387437
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -955.5025 146.9403 246.7240
Red. masses -- 6.2255 1.9524 4.8556
Frc consts -- 3.3488 0.0248 0.1741
IR Inten -- 5.6351 0.2705 0.3427
Part of the log file for the B3LYP optimised TS is reproduced below.
Low frequencies --- -523.8476 -8.2995 -0.0007 -0.0006 0.0003 12.3445
Low frequencies --- 19.1929 136.0310 204.0275
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
2.9563577 3.0722585 0.8391180
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -523.8473 135.9803 204.0138
Red. masses -- 8.2436 2.1661 3.9530
Frc consts -- 1.3328 0.0236 0.0969
IR Inten -- 5.8602 0.7228 0.9950
Both have one negative imaginary frequency; for the AM1 level of theory this is at -955.5cm-1 and for the B3LYP this is at -523.8 cm-1. The most important part of this information is the fact that there is a negative frequency. However, tentatively, the magnitude of the wavenumber can be analysed further. For both transiton states this absorption corresponds to the movement of the terminal carbon atoms in the below fashion.
| AM1 | B3LYP |
|---|---|
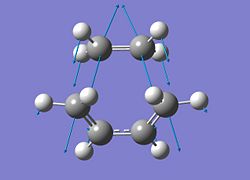 |
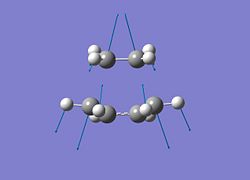 |
In the B3LYP optimised structure, the distance between the terminal carbons is 2.27Å and the in the AM1 optimised structure this distance is reduced to 2.12Å. For normal IR absorptions, the bond length correlates with the wavenumber; the longer the bond the smaller the wavenumber. It is possible that this same theory can be applied to these negative vibrations. The scheme of these vibrations implies that the bond making is synchronous as both terminal carbon atoms approach eachother at the same time. The 1st "real" vibration is a twisting motion of both the molecules as can be seen below.
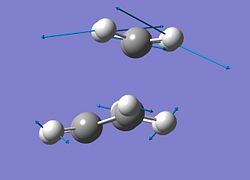
This twisting motion would inhibit concerted bond formation therefore it is possible that asynchrnous bond formation occurs. Literature suggests that both types of bond formation are possible. This could be investigated further using better basis sets etc.
The energies of these transition states has not been compared due to the differences in the methods; these numbers are meaningless. The earlier comparisson between the reactants and TS was made and, as expected, the TS was higher in energy.
Reaction between cyclohexadiene and maleic anhydride
The optimisations and frequencies were all carried out using only the AM1 level of theory due to the time constraints imposed. Ideally this reaction should be studied at a higher level of theory e.e. B3LYP/6-31G* but the presence of heteroatoms and the more complicated structure renders this computationally expensive .
The results genereated by the low level AM1 basis set are unlikely to be very good. This is because the AM1 basis set is based on on the Neglect of Differential Diatomic Overlap integral approximation and in a molecules with large stereoelectronic effects this is likely to lead to inaccurate results. However, trends, etc. will be unaffected and the results should still be valid at this level.
The regioselectivity of the Diels-Alder reaction can be easily studied using this reaction. Maleic Anhydride is a potent dieneophile and reacts with cyclohexa-1,3-diene to give the endo adduct. This is hypothesised to be due to secondary orbital overlap between 2 non bonding pair of atoms due to favourable overlap between the HOMOs and LUMOs This can be rationalised by examination of the transition states of the endo and exo form.
The transition state was built by positioning the 2 fragments 2.2Å apart and optimising using the TS(Berny) option using the Semi Emperical AM1 level of theory.
The exo fragment was created first, optimised and a frequency analysis performed. The below structure was generated.
Vibrationjwp108 |
The log file of the frequency analysis was checked for convergence. An exerpt is copied below.
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000404 0.001800 YES RMS Displacement 0.000128 0.001200 YES Predicted change in Energy=-1.536594D-09 Optimization completed. -- Stationary point found.
This clearly shows convergence has been reached. A transition state should only have one negative frequency so the frequency output is reproduced below.
Low frequencies --- -811.1700 -5.0421 -4.4824 -2.5222 0.0373 0.0925
Low frequencies --- 0.3650 60.5780 123.7527
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
17.3384531 16.5755928 8.9910849
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -811.1700 60.5779 123.7526
Red. masses -- 7.0401 4.4862 7.1667
Frc consts -- 2.7293 0.0097 0.0647
IR Inten -- 96.7100 0.5536 0.0413
The one negative frequency at -811.2cm-1 corresponds to bond formation beween the alkene carbon atoms in maleic anhydride and 2 of the diene carbon atoms as shown below.
The energy of the transition state is -0.05050326 hartree.
The endo transition state was generated and analysed using the same level of theory. The below structure was generated.
Vibrationjwp108 |
An exerpt of the logfile showing convergence is shown below.
Item Value Threshold Converged? Maximum Force 0.000081 0.000450 YES RMS Force 0.000013 0.000300 YES Maximum Displacement 0.000348 0.001800 YES RMS Displacement 0.000078 0.001200 YES Predicted change in Energy=-2.179793D-08 Optimization completed. -- Stationary point found.
The frequency analysis was also checked to see if there was only 1 negative vibration.
Low frequencies --- -805.6410 -3.4323 -3.3115 -0.1940 0.0142 0.1486
Low frequencies --- 1.2248 62.4135 111.6844
****** 1 imaginary frequencies (negative Signs) ******
Diagonal vibrational polarizability:
18.5014230 23.6113092 8.9775861
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- -805.6410 62.4132 111.6844
Red. masses -- 6.6982 4.3308 6.7985
Frc consts -- 2.5615 0.0099 0.0500
IR Inten -- 71.2688 1.5374 3.4237
This negative frequency corresponds to the below vibration; the formation of a bond between the 2 molecules .
The energy of this transition state is -0.05129428 hartree. This corresponds to an energy difference of 0.00079102 hartree or 2.0764275 kJ/mol in favour of the endo transition state; a surprising result. Experimentally it is known that the exo form is primarily formed and this can rationalised by compaing the molecular orbitals for both transiton states.
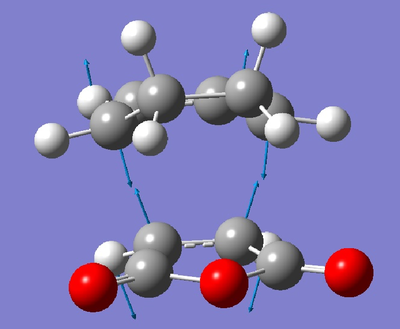
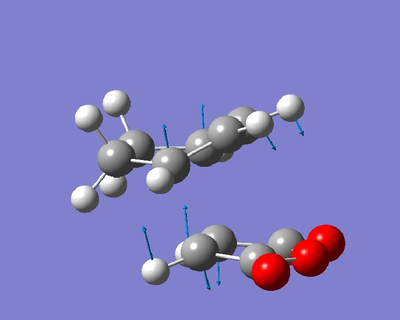
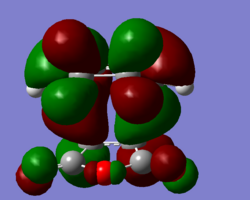
Secondary orbital overlap was not observed in the HOMO of the endo TS but was observed in the HOMO-1 so this orbital is reproduced below.
| HOMO (exo) | HOMO (endo) |
|---|---|
 |
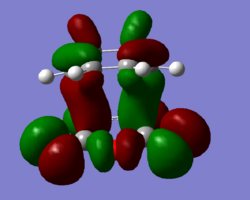 |
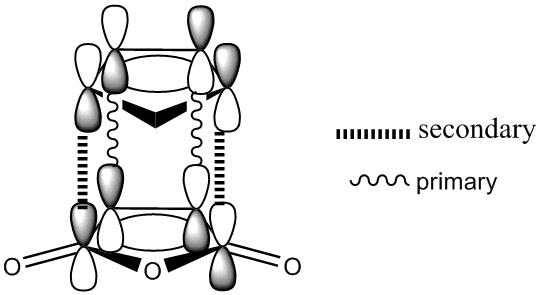
From these diagrams, the secondary orbital overlap can clearly be seen in the form of the large orbtials bridging both molecules. The shape can be rationalised with reference to this qualatative diagram below. Cyclopentadiene is used due to the availability of the 3D stucture as a template in ChemDraw but the theory is the same as for Cyclohexadiene.
Clearly what has happened is that the primary and secondary overlapping orbitals of the same phase have mixed together leading to a bridging molecular orbital as seen above. No nodal plane can be seen between the primary and secondary orbital overlapping orbitals on the same side of the transition state but there is a nodal plane through the σv plane. This transiton state is antisymmetric. A further factor disfavouring the exo state is steric hinderance; the distance between the hydrogen atoms at the back of the maleic anhydride molecule and the cyclohexa-1,3-diene moeity is only 2.64Å in the exo form whilst in the endo form this distance is increased to 3.08Å. Though this is a small distance, steric repulsions are known to increase exponentially with decreasing distance as per the Leonard Jones potential. The peak attractive force as per the Leonard Jones potential is 2.81Å, any closer and there will be repulsion and any further there will be reduced attraction. By this rule, the interactions in the exo form are strongly repulsive and the interactions in the endo form are mildly attractive, further explaining the endo selectivity in this Diels Alder reaction.
Conclusion
From these results, the primary conclusion to be made is that the endo product is the thermodynamically stable product but the exo product is favoured as the transition state is stabilised to a greater extent through the secondary orbital overlap and the unfavourable steric interactions present in the endo TS are not present. The cause of the thermodynamic stability of the exo product has not been investigated but it is probably due to the electrostatic repulsion resulting from the close proximity of the C=O pi electrons and the hydrogen sybstituents on the bridging carbons. This assertion warrants further analysis of the products and would form the ideal basis for further investigation.
References
1. Brandon G. Rocque; Jason M. Gonzales; Henry F. Schaefer III. An analysis of the conformers of 1,5-hexadiene. MOLECULAR PHYSICS, 2002, VOL. 100, NO. 4, 441-446. DOI: 10.1080/00268970110081412.