Y3C Transition states and Reactivity

Introduction

This section aims to illustrate the 3 different computational techniques that can be utilised in order to analyse the transition state (TS) of a reaction. The TS is the state which has the highest energy along a reaction coordinate, as a result it is the least stable state. In the reaction, the reactants needs to have a certain amount of energy in order to surpass the activation barrier, also known as the transition state energy, and reach the product state. This computational lab allows for calculations leading to the location of the TS. The structure of the TS is crucial in determining the mechanism of a reaction.

A potential energy surface (PES) has a 3N-6 dimension, which coincides to the degrees of freedom that the molecule has, where N is the number of atoms that the molecule possesses. In a 3-D PES, the saddle point (also called the TS), is a local mixami amidst 2 minima, and can be sometimes identified through secondary derivatives as it would be negative in one direction and positive in all other directions.

Nf710 (talk) 22:50, 22 February 2018 (UTC) Your TS is being evaluated in 3N-6 dimensiosn not 2 you get the force constants from diagonalisation of the hessian matrix.

There are 3 calculation methods available in order to determine the structure of the TS.

1. The first and fastest method requires only one step where a guessed structure of the TS is optimised to give an optimised TS. This means that one will need of the TS to quite an extent, furthermore this method is rather unreliable as there is a high chance that the guessed TS is incorrectly drawn.

2. The second method works from a pre-frozen guess structure of the TS where the reacting termini of the reactants are frozen in space before the remaining structure is optimised to a minima. After that, the molecules are optimised as a transition state. This allows for a more reliable representation of the TS. This method is sufficient for Exercise 1.

3. The third method is the longest and most reliable method. Here, one starts by either optimising from the reactants or the products to a minima. For the reactant case, each reactants are optimised to a minima, arranged to resemble the TS and the reacting termini are frozen and the rest of the method 2 is repeated. A similar case occurs with the product; when the product is optimised to a minima, the bonds formed in the reactions are removed, the 2 fragments are arranged to resemble the TS and the reacting termini are frozen and method 2 was used once more. This method allows for the most reliable representation of the TS and is used for Exercise 2 & 3.

In this computational lab, two methods of calculation were used on Gaussian in order to find the TS. During the optimisation, the position of the molecule is decided as it is built in Gaussian. The time-independent Schrödinger equation was solved whilst utilising the Born-Oppenheimer approximation in order to find the energy and the wavefunction φ which represents the electronic states for the fixed nuclear positions and is dependent on on frozen nuclei positions. This is also known as the self-consistent field method (SCF). The two methods employed are the semi-empirical method PM6, which is usually performed first and sometimes followed by the Density Functional Theory (DFT) method B3LYP. The semi-empirical method PM6, although based on the Hartree-Fock formalism, this method uses many approximations based on experimental data in order to solve the Schrodinger equations. This method is usually fast and reliable, but can be easily countered if the environment of the molecule that is being computed is not similar enough to the approximated parameters of this method. The other method is B3LYP, a hydrid functional which utilises the DFT in order to calculate the majority of the Hamiltonian while a small portion still utilises the Hartree-Fock theory to calculate the exchange integral term. B3LYP stands for Becke, 3-parameter, Lee-Yang-Parr and uses a 6-31G basis set as the electronic wavefunction in order to produce more accurate results at the cost of increased calculation time.

Nf710 (talk) 22:50, 22 February 2018 (UTC) Good understanding here the it would have been nice if you coudl have added some equations to explain the methods used. As each method has a slightly different hamiltonian operator

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Great job in the whole section! Well done!)

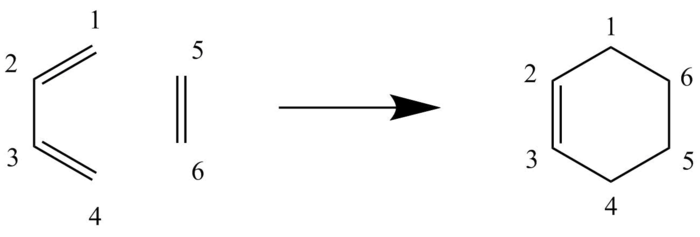
Also known as the Diels-Alder reaction, this exercise investigates the well-known [4+2] cycloaddition between a conjugated diene (butadiene) and a dienophile (ethylene). The electrophilic reaction involves 4 pi-electrons from the diene and 2 pi-electrons from the alkene, and is a popular method to form regio- and stereochemically controlled 6-membered rings.

Method 2 was used to compute the transition state (TS) for this exercise. All steps are optimised to the PM6 level. First, the reactants are optimised to a minimum. The carbons at the reacting termini were then frozen at around 2.20 Å before optimised to a minimum to give a frozen-guess TS. Then finally, the molecule was optimised as a TS and an IRC was performed in order to confirm and locate the transition state.

Analysis of the Molecular Orbitals (MO)

The Lowest Unoccupied Molecular Orbital (LUMO) and the Highest Occupied Molecular Orbital (HOMO) for the reactants and the TS are shown below and its energies were recorded in order to produce the MO diagram as shown in figure 2.

Ethene - HOMO

Ethene - LUMO

Butadiene - HOMO

Butadiene - LUMO

TS - HOMO -1

TS - HOMO

TS - LUMO

TS - LUMO +1

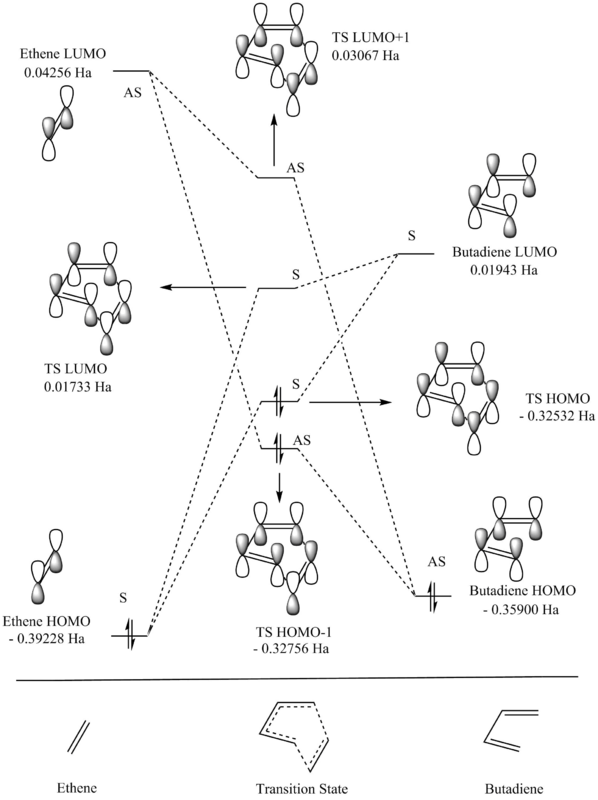
The symmetric TS HOMO and LUMO are formed through the interactions between the HOMO of ethylene and the LUMO of butadiene, both of which are symmetric. On the other hand, the LUMO of ethylene and the HOMO of butadiene, both of which are asymmetric, interacts to give an asymmetric HOMO-1 and LUMO+1. What can be concluded about the requirements for symmetry is that molecular orbitals need to be of the same symmetry in order for the reaction to be allowed, and that the reaction is forbidden when the symmetry of the molecular orbitals aren't the same. The orbital overlap integral, S_AB, is a quantitative measure of orbital overlap of two different atoms. Orbitals of the same symmetry will lead to constructive overlap and gives a non-zero value while orbitals of different symmetry will lead to destructive overlap and an orbital overlap integral of zero. Thus the overlap integral are:

- Non-zero for symmetric-symmetric interaction

- Non-zero for asymmetric-asymmetric interaction

- Zero for symmetric-asymmetric interaction

As observed in the MO diagram, the energy gap between the HOMO and LUMO for butadiene is smaller that those for ethylene due to butadiene being more electron rich than ethylene. Furthermore, in a normal MO diagram, the bonding MO formed should have a lower energy compared to both atomic orbitals (AO) whilst the anti-bonding MO formed should have a higher energy than both AOs. The reason why figure 3 goes against the tide is because the MOs formed corresponds to the transition state where the electrons are very delocalised within the chemical environment of the molecule.

LOG Files

File:Cc5115_ETHENE_MO.LOG

File:Cc5115_BUTADIENE_MO.LOG

File:Cc5115_OPT_MO.LOG

Analysis of the C-C bond lengths

Bond Lengths (Å)	C1-C2	C2-C3	C3-C4	C4-C5	C5-C6	C6-C1
Ethylene					1.36
Butadiene	1.36	1.54	1.36
Transition State	1.38	1.41	1.38	2.11	1.38	2.12
Cyclohexadiene	1.49	1.33	1.49	1.54	1.54	1.54

The numbering of the carbon bonds are according to the labels on figure 1. The typical C-C bond lengths are as follows:

Bond Type	Bond Length (Å)
sp³-sp³ C-C bond	1.54
sp³-sp² C-C bond	1.50
sp²-sp² C-C bond	1.47
sp²-sp² C=C bond	1.34

When the reaction proceeds to the transition state, the sp²-sp² C5-C6 bond (originally ethylene) becomes longer as the carbons starts to change from sp² hybridised to sp³ hybridised. This trait is also apparent with C1-C2 and C3-C4 bonds where it once was the double bonds on butadiene, however, the increase in length of these bonds is less than that of C5-C6 due to the formation of a new double bond between C2 and C3, thus these carbons still remain sp² hybridised. This also leads to the next observation, where the C2-C3 bond decreases in length as it moves from the reactants to the transition state then the product, cyclohexadiene. This is because it is changing from a sp³-sp³ C-C bond to a sp²-sp² C=C bond where the increase in s character shortens the bond lengths. This reaction also leads to the formation of 2 new bonds, namely C4-C5 and C6-C1. The Van der Waals radius of a carbon atom is 1.7 Å, and so the distance between 2 carbon atoms should be 3.4 Å, which is relatively longer than the bonds C4-C5 and C6-C1 which has a length of 2.11 and 2.12 Å respectively. This shows that the bonds are already partially formed in the transition state and they are beginning to interact together. This bond then settled at 1.54 Å in the product which matches with the typical bond length for a sp³-sp³ C-C bond.

Analysis of the vibrations

The animation for the first vibration is shown below. As observed, the formation of the 2 new bonds are synchronous as the reacting termini of butadiene and ethylene approaches each other at the same rate.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

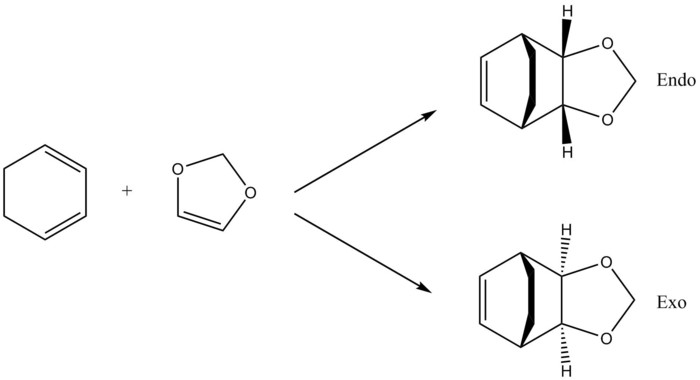
The Diels-Alder reaction between cyclohexadiene and 1,3-dioxole can proceed via either the endo or exo pathways to form 2 products with different stereochemistry. Method 3 was employed in order to compute the TS for this exercise. This time, the structures were further optimised with B3LYP/6-31G method and the results are shown and discussed below.

Analysis of Molecular Orbitals

(Fv611 (talk) Good MO diagrams, but you could have discussed the differences between the endo and exo conformation in terms of the relative energies of their TS MOs. Additionally you forgot to give the endo transition state JMols the correct header.)

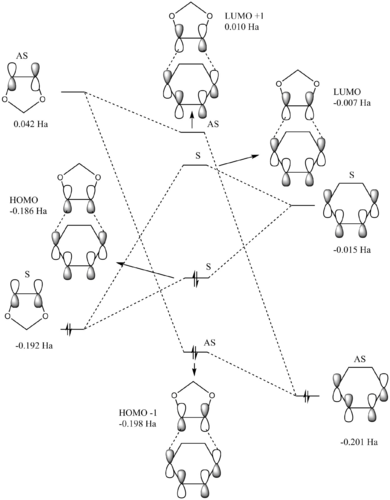
There are two types of Diels-Alder (DA) reactions: one is with a normal electron demand where the dienophile is electron deficient and the diene is electron rich, and the other is with an inverse electron demand where the dienophile is electron rich and the diene is electron deficient.

For a normal electron demand DA reaction, the dienophile low-lying LUMO interacts with the diene HOMO which has a high energy. However, observing the energies of the reactants and the transition states, the MO diagram shows that this particular DA reaction has an inverse electron demand where the dienophile (1,3-dioxole) is electron rich (higher in energy) and the diene (cyclohexadiene) is electron poor (lower in energy). The interaction between the HOMO of 1,3-dioxole and the LUMO of cyclohexadiene thus leads to the HOMO and LUMO of the transition state. Although opposing that of a normal electron demand DA, this reaction still follows the Woodword-Hoffman rule and is thermally allowed.

Similar to exercise 1, MOs of the same symmetry interact; the symmetrical dienophile HOMO and the diene LUMO interacts to give a symmetrical TS HOMO and LUMO, while the asymmetrical dienophile LUMO and diene HOMO gives the asymmetrical TS HOMO-1 and LUMO+1. It is also observable that the endo TS HOMO has a lower energy than the exo TS HOMO which suggests that the endo reaction is favoured. This will be discussed further in the Thermochemistry section of this exercise.

Nf710 (talk) 22:56, 22 February 2018 (UTC) You have just stated the demand of the reaction you have not tried to prove it by looking at the enrgy of the orbitals with a single point energy calculation

ENDO TS - HOMO -1

ENDO TS - HOMO

ENDO TS - LUMO

ENDO TS - LUMO +1

TS - HOMO -1

TS - HOMO

TS - LUMO

TS - LUMO +1

Log Files

File:Cc5115 ENDO B3.LOG

File:Cc5115 PLEASE WORK B3.LOG

Thermochemistry

Reaction Pathway	Reacton Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	+149.70	-77.52
Exo	+157.52	-73.92

As discussed briefly in the introduction, the reactants need to pass the activation barrier (transition state) in order to reach to the products. The table regarding the reaction barriers and energies shows that the activation barrier for the endo reaction is less than that of the exo reaction, more-so confirming that the endo reaction is kinetically favoured. This links to the lower energy that the endo TS HOMO has compared to the exo TS. This observance can be explained by secondary orbital interation (SOI). The 2 non-bonding oxygen p-orbitals containing electron lone pairs can overlap with the LUMO of the diene through space thus stabilising the TS and consequentially lowering reaction barrier. However, the more negative reaction energy of the endo reaction can be explained with sterics; in the exo transition state, the steric interaction between the sp³ bridging carbons and the rest of the 1,3-dioxole structure results in the exo product being higher in energy.

Exo Secondary MO

Endo Secondary MO

Nf710 (talk) 22:59, 22 February 2018 (UTC) The discussion in this section is quite brief. Your energies are also slightly out. It looks like you may have miss calculated the reactants correctly. You have however come to the correct conclusions.

Nf710 (talk) 22:59, 22 February 2018 (UTC) These are very nice J Mols. BUt

Exercise 3: Diels-Alder vs Cheletropic

IRC

IRC for Exo Product	IRC for Endo Product	IRC for Chelatropic Product

IRC (intrinsic reaction coordinate) show how reactions move in space during its reaction to form products. From the IRC animations, it can be seen that the formation of the new bonds differ to that of exercise 1. Here, in the exo and endo pathways, the formation of the 2 new bonds are asynchronous as one bond forms before the other. However, the bonds form synchronously in the chelatropic reaction leading to the symmetrical product.

The IRC reaction pathways also show a smaller activation barrier compared to that of exercise 1. This is because xylylene is highly unstable. Xylylene can exist with 4π electrons making it anti-aromatic, or either with 6π electrons an a diradical which is very unstable. On the flipside, the product formed is aromatic making the DA reaction extremely favourable. Naphthalene forces the diene to be rigid in its positions easing the overlap capabilities of the diene with the dienophile. This can be observed in the animation as naphthalene doesn't have to go through major rearrangements in order to form the products.

In the reaction, naphthalene initially has a C=C bond length of 1.35 Å and a C-C bond length averaging around 1.51 Å. This changes as the product is formed where all the carbon-carbon bonds on the 6 membered rings become 1.47 Å in length suggesting the formation of an aromatic 6-membered ring where the π electrons are delocalised throughout the ring. The change in bond length can also be seen with careful observation of the animations.

Log Files

File:Cc5115 chelatropic IRC.LOG

File:Cc5115 endoex3 IRC.LOG

File:Cc5115 exoex3 IRC.LOG

Thermochemistry

Reaction Pathway	Reacton Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	+79.85	-100.95
Exo	+83.82	-101.59
Chelatropic	+102.16	-157.93

(Your energies are shifted a bit, so your reactants are too high in energy Tam10 (talk) 17:11, 26 February 2018 (UTC))

Significantly resembling to exercise 2, exercise 3 features the endo pathway being kinetically favoured as its activation energy has the least energy compared to the other pathway. Again, this is due to the overlap between the oxygen p-orbitals overlapping with the π-orbitals of the xylylene ring. However, the difference in activation and reaction energies between the exo and endo pathways do not differ that much due to the SOI not contributing significantly in the TS and there are little steric difference between the two products. For the chelatropic product, there is a hugh drop in reaction energy. Observing the product, the large sulfur atom forming a 5-membered ring decreases the ring-strain making the product relatively stable compared to the products from the DA reaction.

Cyclisation at the other reaction site

IRC for Exo Product at reaction site B	IRC for Endo Product at reaction site B

Reaction Pathway	Reacton Barrier (kJ/mol)	Reaction Energy (kJ/mol)
Endo	+110.06	-14.33
Exo	+117.90	-18.78

(These reaction energies should be positive ie endothermic Tam10 (talk) 17:11, 26 February 2018 (UTC))

For this exercise, the Diels-Alder reaction can also take place at the other reaction site as illustrated in the animations. As seen from the table of reaction barrier and energy, the endo product is both kinetically and thermodynamically favoured as its activation energy is lower (TS has lower energy) as well as its reaction energy (product has a lower energy and thus more stable). This alternative pathway, however, is not favoured compared to the previous DA reaction since an aromatic 6-membered ring did not form during this reaction. This leads to higher activation energies and well as higher reaction energies.

Log Files

File:Cc5115 IRC 2 endo.LOG

File:Cc5115 IRC exo.LOG

Conclusion

Gaussian was used to calculate the geometries of the transition states and the TS was validated by a correct imaginary frequency from frequency calculations as well as the correct pathways along the reaction coordinate from IRC. In this exercise, the transition states of the DA and a chelatropic reaction was investigated using the PM6 and B3LYP calculation methods. Exercise 1 investigated the carbon-carbon bond lengths of the reactants, TS and products in the reaction between ethylene and butadiene. The bond lengths matched well with expectations. Exercise 2 investigated the inverse-electron demand DA reaction through the construction of a MO diagram and it was concluded that the requirements for symmetry is that molecular orbitals need to be of the same symmetry in order for the reaction to be allowed. Here, the endothermic pathway gave the kinetically and thermodynamically favoured product as expected. Exercise 3 also investigated the chelatropic reaction alongside the DA reaction and, similar to exercise 2, the endothermic pathway resulted in a kinetically and thermodynamically favoured product. An alternative reaction site was also investigated which was concluded to be less favourable to the original DA reaction site as an aromatic 6-membered ring did not form.