Rep:Mod:cc20082
'Module 2: Chandra Chadalawada
Introduction
Investigating bonding in inorganic compounds can be more complicated than in organic compounds due to many factors including the ionic nature of many compounds, the larger number of electrons in the system and the relative insensitivity of many inorganic nuclei to spectroscopic techniques such as NMR. Fortunately, computational techniques can be used to model such compounds to a relatively high degree of accuracy. These techniques usually revolve around solving the Schrondinger equation for the electronic wavefunctions. Doing this analytically is almost impossible due to extreme complexity of many electron systems due to the huge number of electrons. However, by separating the electronic and nuclear wavefunctions using the Born-Oppenheimer approximation and approximating the electronic wavefunctions using a basis set and minimising the energy of the system the properties of inorganic systems can be calculated to a relatively high degree of accuracy. The accuracy of such methods, however depends on the basis sets and the methods used to calculate the minimum.
The optimisation of BH3
BH3 was investigated using the Gaussview program for Windows. The trigonal planar BH3 molecule was constructed with the bond lengths all set to 1.5Å. The structure was investigated using the B3LYP method and the 3-21G basis set. The below summary of results was generated.
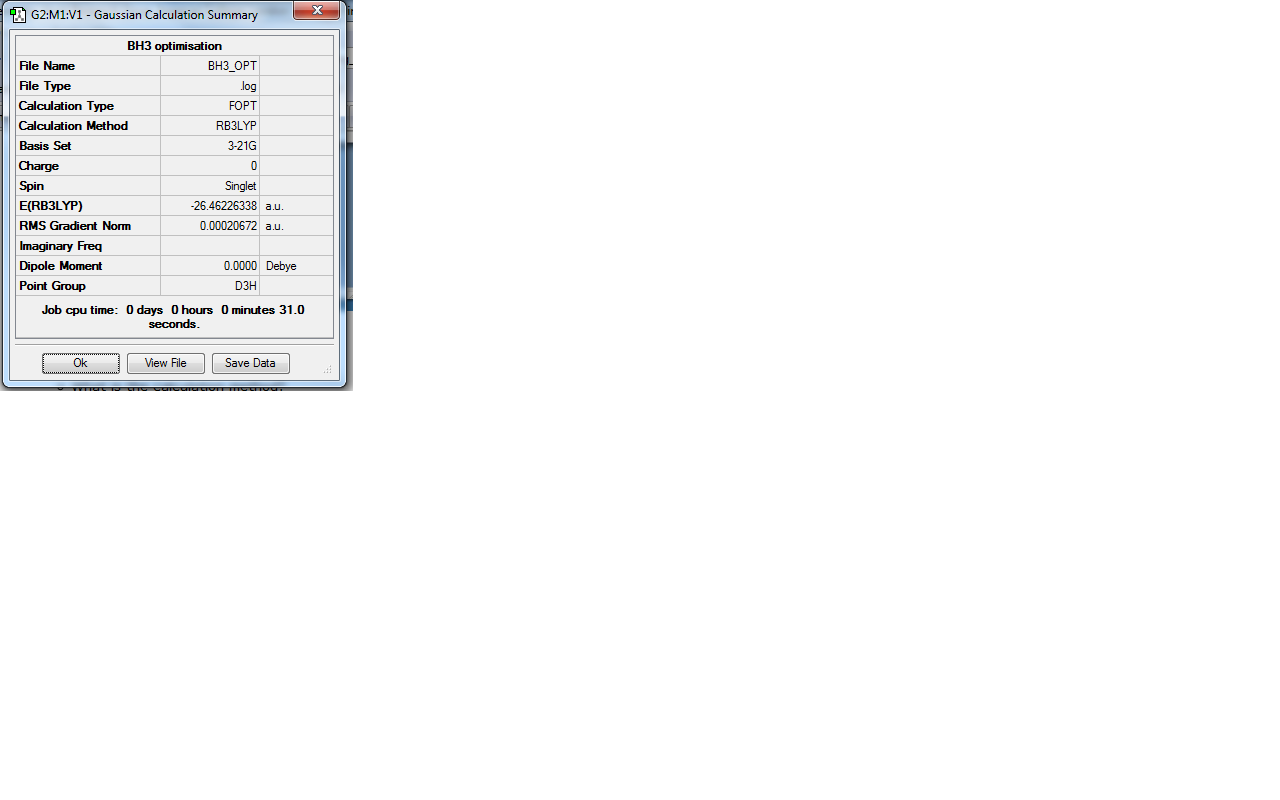 The success of the calculation can be roughly gauged using the gradient; a minima would have a gradient of 0. As can be seen the gradient is 0.00020672, implying a minimum has been generated. The spin state is a singlet, agreeing with LCAO theory (to be discussed later). The lack of a dipole moment is in agreement with the trigonal planar geometry expected. It is important to note, though a final energy in atomic units has been generated, this is specefic to the method used and cannot be easily compared with the total energy of other molecules. Further information can be gleaned with reference to the text output which is reproduced below:
The success of the calculation can be roughly gauged using the gradient; a minima would have a gradient of 0. As can be seen the gradient is 0.00020672, implying a minimum has been generated. The spin state is a singlet, agreeing with LCAO theory (to be discussed later). The lack of a dipole moment is in agreement with the trigonal planar geometry expected. It is important to note, though a final energy in atomic units has been generated, this is specefic to the method used and cannot be easily compared with the total energy of other molecules. Further information can be gleaned with reference to the text output which is reproduced below:
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
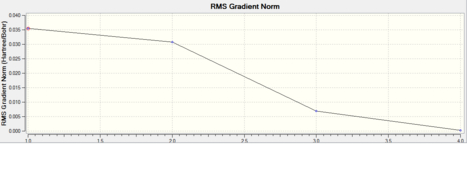
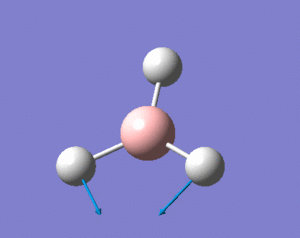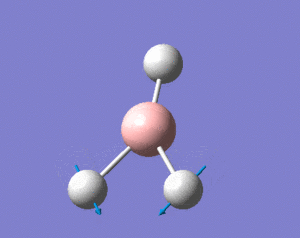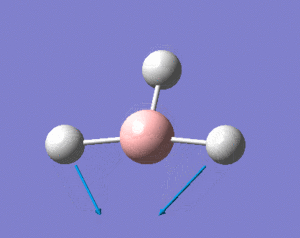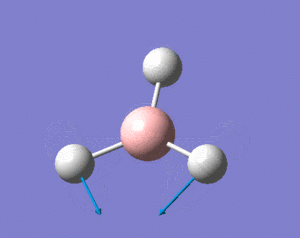
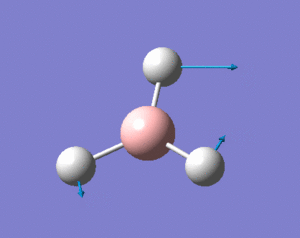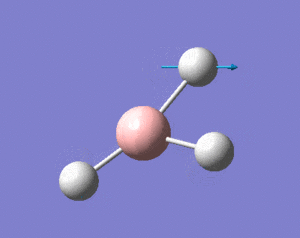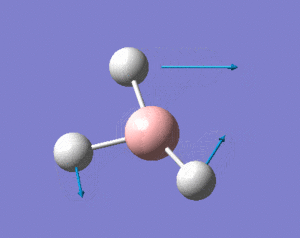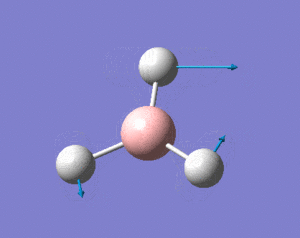
This shows the bond lengths ,which are all 1.1935Å, and the bond angles, which are all 120o. Further evidence to the success of the calculations is shown by the derivatives of the bond lengths and angle which are all almost 0. The D1 value of 180o tells us the molecule is planar, as expected. Further information can be gathered from the below graphs.
The graphs reflect the speedy computation of 33 seconds; only 4 steps were needed for optimisation. The decrease in energy reflects the increase in bonding between the central boron atom and the surrounding hydrogen atoms which serve to stabilise the molecule. The equilibrium bond length of 1.1935Å generated is through stepwise contraction of the bond from 1.5Å and this is reflected in the stepwise stabilisation of the molecule. Any further decrease in bond length would lead to destabilisation through internuclear replulsion.