Rep:Mod:cb5418
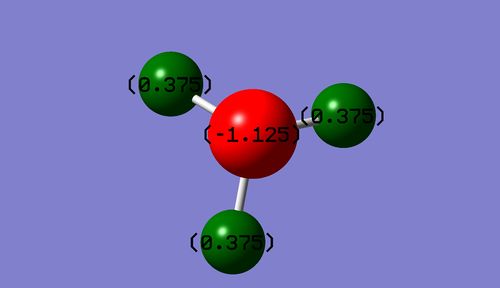
NH3 molecule
NH3 molecule |
Link to .log file
Summary of results
| Molecule name | Ammonia |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) in atomic units (a.u.) | -56.55776873 |
| RMS gradient (a.u.) | 0.00000485 |
| Point group | C3V |
| N-H bond distance (Å) | 1.02 |
| H-N-H bond angle (°) | 106 |
"Item" table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986275D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
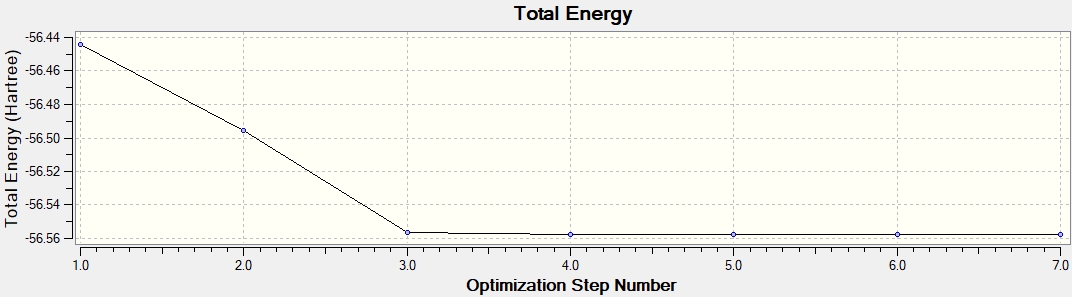
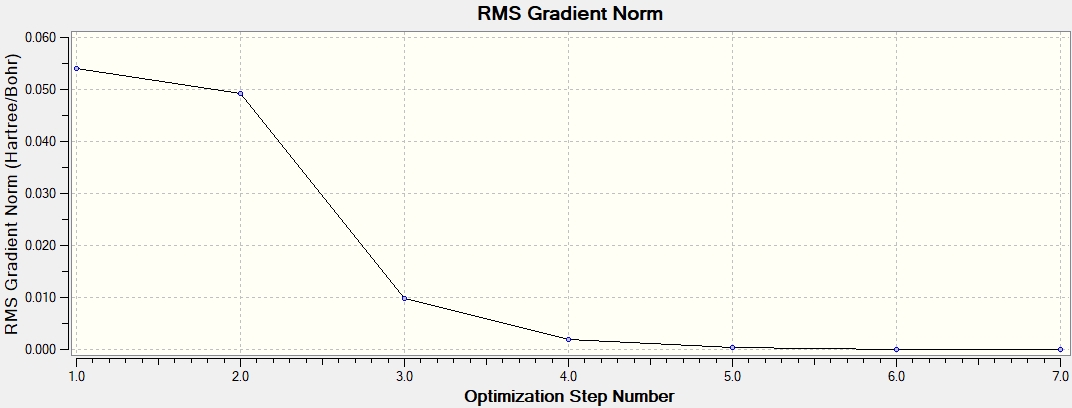
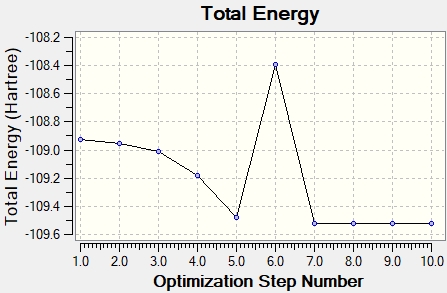
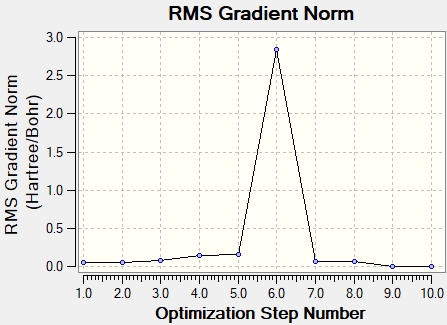
Graphs showing how the energy and gradient have changed over the optimisation
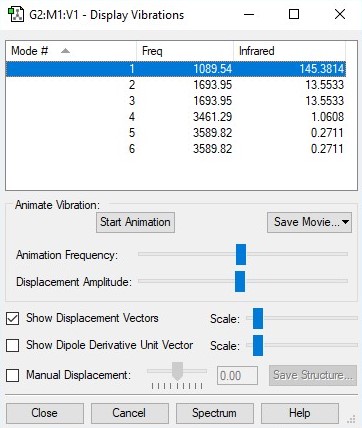
Animating the vibrations
| wavenumber cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| symmetry | A1 | E | E | A1 | E | E |
| intensity arbitary units | 145 | 13.6 | 13.6 | 1.06 | 0.271 | 0.271 |
| image |  |
 |
 |
 |
 |
|
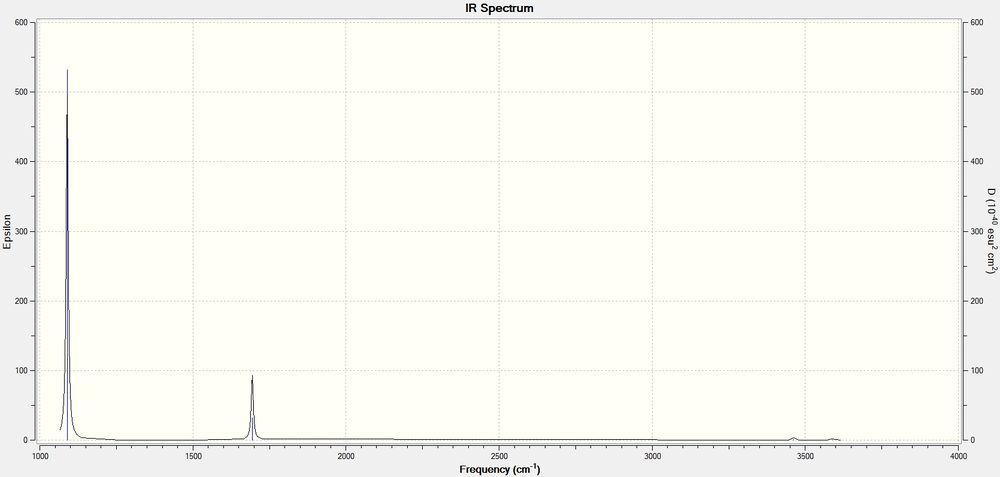
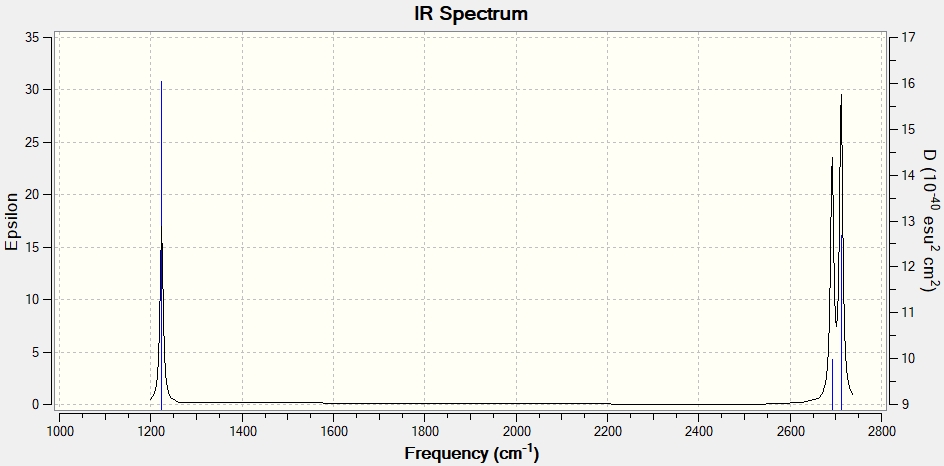
According to the 3N-6 rule, 6 modes are expected for this molecule. The 2 modes with 1694 cm-1 wavenumber and the other 2 modes with 3590 cm-1 wavenumber are degenerate. The vibrations with the following wavenumbers are "bending" vibrations: 1090 cm-1 and 1694 cm-1. The vibrations with the following wavenumbers are "bond stretch" vibrations: 3461 cm-1 and 3590 cm-1. The mode with the wavenumber 1090 cm-1 and 3461 cm-1 are highly symmetric. The mode with the wavenumber 1090 cm-1 is the mode know as the "umbrella" mode. In an experimental spectrum of gaseous ammonia, four bands are expected to be seen (two strong bands and two very weak bands) as shown in the IR spectrum below.
Charge analysis
The charge on the nitrogen atom is expected to be negative and the charges on the hydrogen atoms are expected to be positive, since the nitrogen atom is a more electronegative atom than hydrogen which means more electron density around the nitrogen atom. The partial negative charge on the nitrogen atom is balanced out by the partial positive charges on the hydrogen atoms making the ammonia molecule neutral.
N2 molecule
N2 molecule |
Link to .log file
Summary of results
| Molecule name | Nitrogen |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) in atomic units (a.u.) | -109.52412868 |
| RMS gradient (a.u.) | 0.00003369 |
| Point group | D∞h |
| N≡N bond distance (Å) | 1.11 |
| N≡N bond angle (°) | 180 |
"Item" table
Item Value Threshold Converged?
Maximum Force 0.000058 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000013 0.001800 YES
RMS Displacement 0.000026 0.001200 YES
Predicted change in Energy=-1.063903D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Graphs showing how the energy and gradient have changed over the optimisation
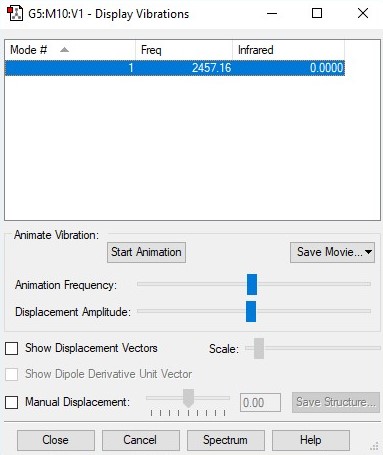
Animating the vibrations
| wavenumber cm-1 | 2457 | |
| symmetry | SGG | |
| intensity arbitary units | 0 | |
| image |  |
Charge analysis
H2 molecule
H2 molecule |
Link to .log file
Summary of results
| Molecule name | Hydrogen |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) in atomic units (a.u.) | -1.17853936 |
| RMS gradient (a.u.) | 0.00000017 |
| Point group | D∞h |
| H-H bond distance (Å) | 0.74 |
| H-H bond angle (°) | 180 |
"Item" table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
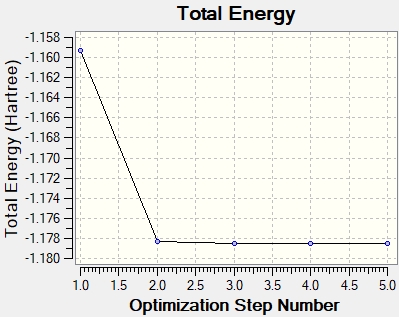
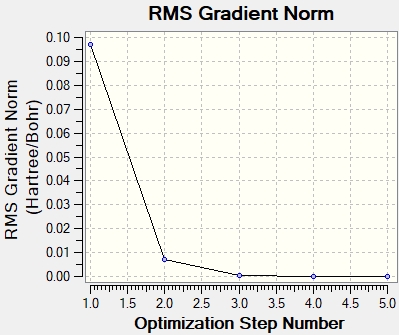
Graphs showing how the energy and gradient have changed over the optimisation
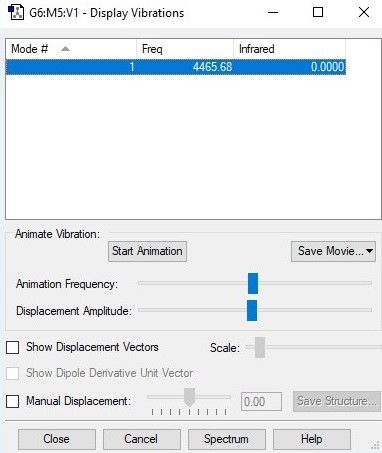
Animating the vibrations
| wavenumber cm-1 | 4466 | |
| symmetry | SGG | |
| intensity arbitary units | 0 | |
| image | |
Charge analysis
Structure and Reactivity
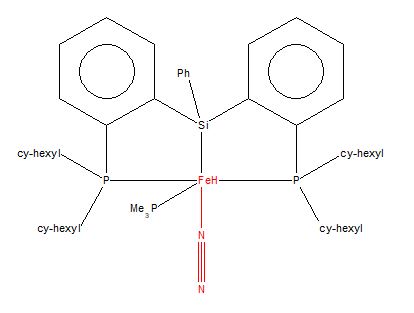
Transition metal complex that coordinates N2
The transition metal complex founded is called (bis(2-(dicyclohexylphosphino)phenyl)(phenyl)silyl)-hydrido-dinitrogen-(trimethylphosphino)-iron. The unique identifier for the structure is VEJRUA and the deposition number is 1547288. The N≡N bond length in this transition metal complex is 1.149 Å, whereas the N≡N bond length of N2 is 1.1055 Å.
From the N≡N bond lengths mentioned above, the N≡N bond length of the transition metal complex is longer than the N≡N bond length of N2. This is because the transition metal complex, in this case Fe, takes away some of the electron density from the N atom in order to form the Fe-N bond. Consequently, there is less electron density shared between the N≡N, thus the N≡N in the transition metal complex is not only longer but also weaker. Another reason is due to the fact that the transition metal complex processed by the programme ConQuest is in solid state, whereas the N2 molecule is in a gaseous phase. Therefore, the N≡N bond length differs.
When comparing these results using the computational method and the experimental method then there are bound to be some errors. The errors may arise due to the limited parameters used to compute the results, thus a better computational method may be used which takes in account more parameters in order to minimise the errors between the computational and experimental methods.
Determining the energy for the Haber-Bosch process
Haber-Bosch process: N2 + 3H2 -> 2NH3
E(NH3)=-56.55776 a.u.
2*E(NH3)=-113.11552
E(N2)=-109.52412 a.u.
E(H2)=-1.17853 a.u.
3*E(H2)=-3.53559 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05881 a.u.=(-0.05881*2625.5) kJ/mol=-146.5 kJ/mol
H2S molecule
H2S molecule |
Link to .log file
Summary of results
| Molecule name | Hydrogen sulfide |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) in atomic units (a.u.) | -399.38286251 |
| RMS gradient (a.u.) | 0.02273972 |
| Point group | C2V |
| S-H bond distance (Å) | 1.35 |
| H-S-H bond angle (°) | 93 |
"Item" table
Item Value Threshold Converged?
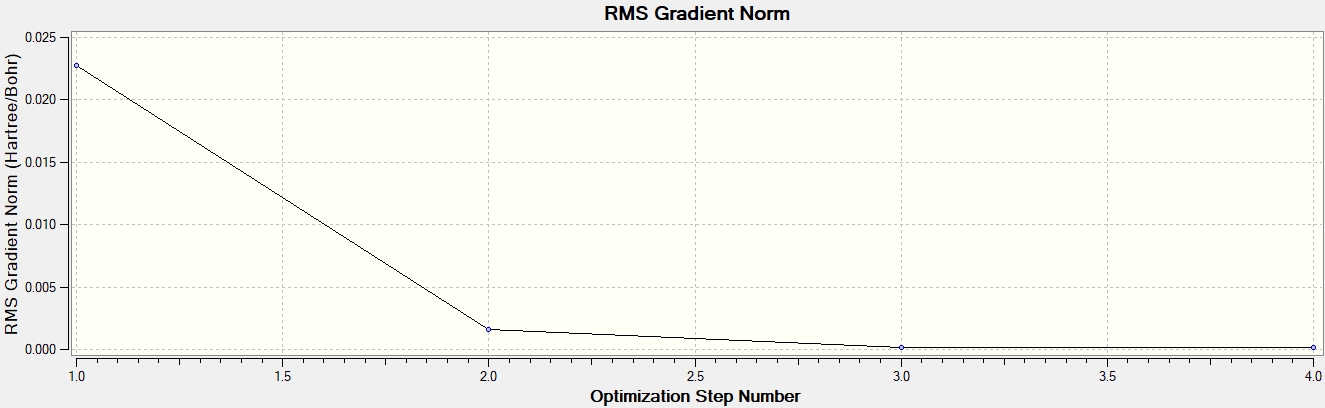
Maximum Force 0.000175 0.000450 YES
RMS Force 0.000145 0.000300 YES
Maximum Displacement 0.000472 0.001800 YES
RMS Displacement 0.000386 0.001200 YES
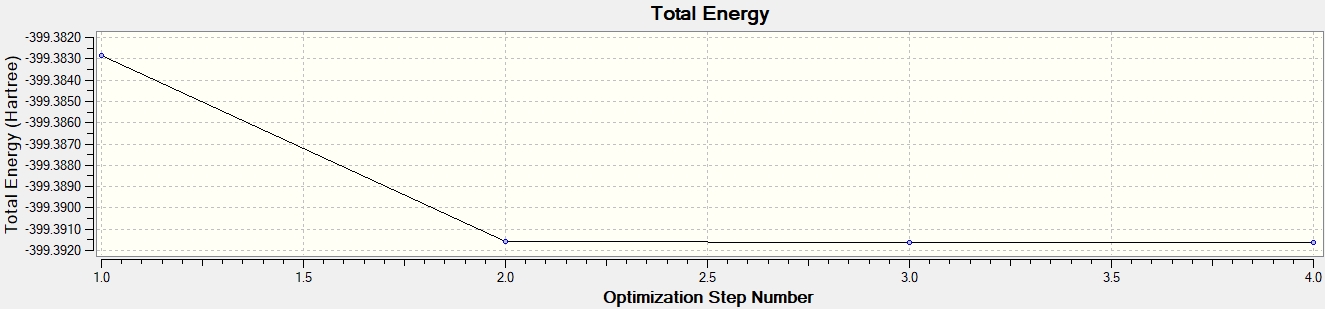
Predicted change in Energy=-1.208488D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3474 -DE/DX = 0.0002 !
! R2 R(1,3) 1.3474 -DE/DX = 0.0002 !
! A1 A(2,1,3) 92.681 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Graphs showing how the energy and gradient have changed over the optimisation
Animating the vibrations
| wavenumber cm-1 | 1224 | 2692 | 2712 |
| symmetry | A1 | A1 | B2 |
| intensity arbitary units | 4.92 | 6.73 | 8.62 |
| image |  |
 |
|
Three modes are expected from the 3N-6 rule. There are no degenerate modes for this molecule. The mode with the wavenumber 1224 cm-1 is a "bending" vibration and the other two modes which have the wavenumber 2692 cm-1 and 2712 cm-1 are "bond stretch" vibrations. The modes with 1224 cm-1 and 2692 cm-1 are highly symmetric. For the experimental spectrum of gaseous hydrogen sulfide, 3 bands are expected to be seen as shown in the IR spectrum below.
Charge analysis
There is a partial negative charge on the sulfur atom and partial positive charges on the hydrogen atoms. This is because sulfur is a more electronegative atom than hydrogen, therefore there is a greater electron density around the sulfur atom which induces the partial negative charge on it.
Molecular orbitals
| Which AOs contribute to the MO? | 2p(x,y or z) | One 3s orbital of sulfur and two 1s orbitals of hydrogen | One 3p orbital of sulfur and two 1s orbitals of hydrogen | One 3p orbital of sulfur | One 3p orbital of sulfur and two 1s orbitals of hydrogen |
| Is the MO bonding, antibonding, a mixture or non-bonding? | non-bonding | bonding | bonding | non-bonding | antibonding |
| Is the MO deep in energy, in the HOMO/LUMO region or high in energy? | deep in energy | slightly deep in energy | slightly deep in energy | HOMO | LUMO |
| Is the MO occupied or unoccupied? | occupied | occupied | occupied | occupied | unoccupied |
| What effect will your MOs have on bonding? | non-bonding p-orbital | σ-bonding giving a σ bond | σ-bonding giving a σ bond | non-bonding p-orbital | σ-bonding giving a σ* anti-bond |
| Additional comments | The only contributing AO is the 3p orbital from sulfur, it does not interact with any other orbital, hence non-bonding. | There are 3s AOs one from each atom that is in phase with one another, giving a totally bonding MO. | Although the two s orbitals from each hydrogen are not in phase, they are in turn in phase with the p orbital from sulfur giving rise to more bonding character than antibonding character. | Again, no contributions from either of the hydrogn atoms, hence non-bonding. | All the orbitals are out of phase with each other, therefore it is antibonding. |
| Images of the molecular orbitals |  |
 |
 |
 |
|
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES - good explanation about the charges and vibrations. Experimentally you would not expect to see the very small vibrational bands, so only two peaks would be visible.
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
However you have given a bond angle of 180 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES - Good details included about the bonding.
Haber-Bosch reaction energy calculation 0.5/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
No you haven't written any explanation for this part.
Your choice of small molecule 5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - excellent MO explanations.
Independence 0/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
No independent work included.