Rep:Mod:cb2811IComp

Inorganic Computational Lab

Optimization

BH₃ molecule

Optimization 3-21g

File:CB BH3 OPT.txt

• File Name = CB_BH3_Opt
• File Type = .log
• Calculation Type = FOPT
• Calculation Method = RB3LYP
• Basis Set = 3-21G
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -26.46226429 a.u. ~ -26.462 a.u. (approximation made considering an error of 10 kJmol^-1, i.e. 0.00381 a.u.)
• RMS Gradient Norm = 0.00008851 a.u.
• Imaginary Freq =
• Dipole Moment = 0.0003 Debye ~ 0.00 Debye (approximation to an accuracy of 2 decimal places, i.e. 0.01 Debye)
• Point Group = CS
• Job cpu time: 0 days 0 hours 0 minutes 24.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000709     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672478D-07
 Optimization completed.
    -- Stationary point found.

Optimized B-H bond length: 1.19 Å
Optimized H-B-H bond angle: 120.0 deg

Optimization 631g(dp)

File:CB BH3 OPT 631G DP.txt

• File Name = CB_BH3_OPT_631g_dp
• File Type = .log
• Calculation Type = FOPT
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -26.61532360 a.u. ~ -26.615 a.u.
• RMS Gradient Norm = 0.00000707 a.u.
• Imaginary Freq =
• Dipole Moment = 0.0001 Debye ~ 0.00 Debye
• Point Group = CS
• Job cpu time: 0 days 0 hours 0 minutes 8.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000061     0.001800     YES
 RMS     Displacement     0.000038     0.001200     YES
 Predicted change in Energy=-1.069388D-09
 Optimization completed.
    -- Stationary point found.

Optimized B-H bond length: 1.19 Å
Optimized H-B-H bond angle: 120.0 deg

GaBr₃ molecule

Optimization with LanL2DZ

File:CB GaBr3 opt LanL2DZ.txt

DOI:10042/27605

• File Name = log_88479 GaBr3 opt LanL2DZ second output
• File Type = .log
• Calculation Type = FOPT
• Calculation Method = RB3LYP
• Basis Set = LANL2DZ
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -41.70082783 a.u. ~ -41.701 a.u.
• RMS Gradient Norm = 0.00000016 a.u.
• Imaginary Freq =
• Dipole Moment = 0.0000 Debye ~ 0.00 Debye
• Point Group = D3H
• Job cpu time: 0 days 0 hours 0 minutes 27.7 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282686D-12
 Optimization completed.
    -- Stationary point found.

Optimized Ga-Br bond length: 2.35 Å
Optimized Br-Ga-Br bond angle: 120.0 deg

The computed Ga-Br bond length = 2.35 Å is not far from the literature value for the Ga-Br bond length of Ga₂Br₄•2(dioxane) = 2.31 Å. This result shows that this computational method gives good predictions of the real geometry of the molecule.

BBr₃ molecule

Mixed Optimization with 631g(d,p)

File:CB BBr3 OPT MIX.txt

DOI:10042/27609

• File Name = CB_BBr3_OPT_MIX
• File Type = .log
• Calculation Type = FOPT
• Calculation Method = RB3LYP
• Basis Set = Gen
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -64.43645436 a.u. ~ -64.436 a.u.
• RMS Gradient Norm = 0.00000713 a.u.
• Imaginary Freq =
• Dipole Moment = 0.0004 Debye ~ 0.00 Debye
• Point Group = CS
• Job cpu time: 0 days 0 hours 0 minutes 35.5 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000016     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000054     0.001800     YES
 RMS     Displacement     0.000028     0.001200     YES
 Predicted change in Energy=-9.615695D-10
 Optimization completed.
    -- Stationary point found.

Optimised B-Br bond length: 1.93 Å
Optimised Br-B-Br bond angle: 120.0 deg

Comparison between BH₃ and BBr₃ Bond Lengths

Table 1. Bond Lengths comparison

	BH3	GaBr3	BBr3
Bond length (Å)	1.19	2.35	1.93

In order to compare the bond lengths of BH₃, GaBr₃ and BBr₃ it is worthed recalling that the bond length depend on the atoms size and the difference in electronegativity between the atoms involved. By comparing the results in Table 1 we can observe how changing the ligands and the central atom of the compound affects the bond length.
BBr₃ bond length is larger than BH₃ since Br is a larger atom than H (i.e. has a larger Van der Waal radius) and has more diffuse orbitals, which have a smaller overlap with the B AO. On the other hand, the fact that Br is more electronegative than H makes the B-Br distance reduce slightly; however, this effect is minor compared to the effect of the size of the nuclei.
By changing the central atom from B to Ga (while keeping the same ligands, i.e. Br) an increase in bond length is observed. Again, this is a consequence of the greater Van der Waals radius of Ga compared to B, which determines a greater Ga-Br distance. In this case the smaller electronegativity of Ga compared to B enhances the Ga-Br bond distance, since the two atoms "are not pulled close to each other" as in BBr₃.
Sometimes GaussView does not show bonds where they are expected, but this does not mean that the bonds are not present. In fact, the bonds are present but they are not shown in GaussView since they exceed the program range within which a bond is defined.
A bond is an interaction which arises from the sharing (covalent bond) or an exchange of electrons (ionic bond) between two atoms. This type of interaction is represented by a line.

Frequency analysis

BH₃ molecule

File:CB BH3 FREQ.txt

• File Name = CB_BH3_FREQ_FINE
• File Type = .log
• Calculation Type = FREQ
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -26.61532364 a.u. ~ -26.615 a.u.
• RMS Gradient Norm = 0.00000215 a.u.
• Imaginary Freq = 0
• Dipole Moment = 0.0000 Debye ~ 0.00 Debye
• Point Group = D3H
• Job cpu time: 0 days 0 hours 0 minutes 7.0 seconds.

Low frequencies ---  -11.7227  -11.7148   -6.6070    0.0008    0.0278    0.4278
Low frequencies --- 1162.9743 1213.1388 1213.1390

It is worth noting that the first time the frequency analysis was attempted the low frequencies had different values than those found in Dr Hunt script. This was due to the fact that the point group of the molecule was CS rather than D_3h. Thus, in order to impose the correct point group (i.e. D_3h), the original BH₃ molecule file was optimized in GaussView adding keywords to increase the accuracy of the calculation. The full optimization code used was:

# opt=tight b3lyp/6-31g(d,p) geom=connectivity scf=conver=9 int=ultrafine

0 1

Then, the frequency analysis calculation was run with the following code:

# freq b3lyp/6-31g(d,p) geom=connectivity int=ultrafine scf=conver=9

0 1

This resulted in the low frequencies reported above, which are much closer to those provided by Dr Hunt because the point group of the molecule is now D_3h.

Table 2. Vibrations of BH₃

no.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry D3h point group
1	The H atoms are in the same plane and move up and down in a concerted motion, while the B atom moves in the opposite direction	1163	93	A2"
2	The H atoms are all in the same plane as B and 2 of them bend towards and outwards each other. The third H atom (the LHS one) oscillates towards the RHS H atom while this is bending towards the upper H.	1213	14	E'
3	The upper H atom is stationary, while the other 2 H atoms bend towards and outwards each other in the same plane.	1213	14	E'
4	The B atom is stationary, while the three H atoms, all in the same plane, bend in a concerted motion towards and forwards B	2583	0	A1'
5	The upper H atom is stationary, the other 2 H atoms move alternatively towards and forwards the B atom.	2716	126	E'
6	The 2 lower H atoms stretch symmetrically, while the third H atom (upper one) stretches asymmetrically compared to the other two. The B atom is slightly moving symmetrically towards and forwards the upper H atom.	2716	126	E'

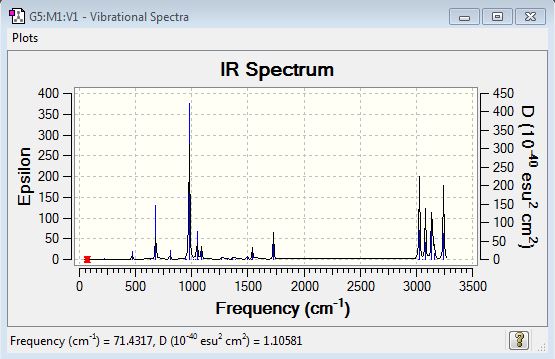
The IR spectrum of BH₃ shows only 3 peaks rather than 6 (which corresponds to the no. of vibrational modes). The reason for that is that the A₁' vibrational mode is IR inactive, i.e. it does not have a change in dipole moment (intensity = 0.0), hence no peak corresponding to this vibration is observed on the spectrum. Furthermore, two pairs of vibrational modes are degenerate (E'), thus only one IR peak per pair is observed on the spectrum. Therefore, the three peaks observed correspond to the A₂"(1163 cm^-1), E'(1213 cm^-1) and E' (2716 cm^-1) vibrational modes.

GaBr₃ molecule

File:CB GaBr3 FREQ.txt

DOI:10042/27615

• File Name = CB_GaBr3_FREQ
• File Type = .log
• Calculation Type = FREQ
• Calculation Method = RB3LYP
• Basis Set = LANL2DZ
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -41.70082783 a.u. ~ -41.701 a.u.
• RMS Gradient Norm = 0.00000011 a.u.
• Imaginary Freq = 0
• Dipole Moment = 0.0000 Debye ~ 0.00 Debye
• Point Group = D3H
• Job cpu time: 0 days 0 hours 0 minutes 15.3 seconds.

Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2010
Low frequencies ---   76.3744   76.3753   99.6982

The lowest "real" normal modes are the degenerate E' modes with vibration frequency of 76 cm^-1.

Table 3. Vibrations of GaBr₃

no.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry D3h point group
1		76	3	E'
2		76	3	E'
3		100	9	A2"
4		197	0	A1'
5		316	57	E'
6		316	57	E'

Comparison between BH₃ and GaBr₃ vibrational frequencies

Table 4. BH₃ vs GaBr₃ vibrational frequencies comparison

Frequency (cm-1)		Symmetry D3h point group
BH3	GaBr3	BH3	GaBr3
1163	76	A2"	E'
1213	76	E'	E'
1213	100	E'	A2"
2583	197	A1'	A1'
2716	316	E'	E'
2716	316	E'	E'

Table 4 shows that the vibrational frequencies of BH₃ are greater than those of GaBr₃. Since the frequency, ν, is directly proportional to the energy of the vibration, as shown by the equation E=hν, this means that more energy is needed to make BH3 vibrate than for GaBr₃. This can be rationalised by considering that Ga and Br atoms have a larger Van der Waals radii than B and H, thus the Ga-Br bond orbitals overlap is smaller than B-H one, i.e. resulting in weaker bonds. The fact that Ga-Br bonds are weaker than B-H ones justifies the higher ease of vibration (i.e. bond stretching and bending) of GaBr₃ compared to BH₃. A rigorous explanation of this observation is obtained by considering the formula of the vibrational frequency of a simple harmonic oscillator:

$\nu =\frac{1}{2\pi }\sqrt{\frac{k}{\mu }}.$

where μ is the reduced mass, and k the spring constant. This formula shows that ν is inversely proportional to the mass of the molecule and directly proportional to k (k is a measure of the strength of the bond, thus, the lower the value of k, the weaker the bond and viceversa). Hence, GaBr₃, which has a higher molecular weight and a lower k value than BH₃, has lower ν than BH₃.

The comparison between the normal modes of GaBr₃ and BH₃ shows that, while the three highest vibrational modes maintain the same order, the A₂" mode in GaBr₃ has a higher vibrational frequency than in BH₃. In fact, A₂" is the mode with the lowest vibrational frequency in BH₃, while in GaBr₃ it is the forth highest vibrational mode, with frequency higher than the two degenerate E' modes. This is explained by considering that A₂" mode involves the ligand atoms moving up and down in the same plane in a concerted motion, while the central atom moves in the opposite direction. The Br atoms have more electrons and are larger (i.e. their orbitals are more diffused) than H atoms, thus, they experience a greater electronic and steric repulsion between each other than H atoms. Hence, this explains why the A₂" mode is higher in energy in GaBr₃ than in BH₃.

The IR spectra of the two compounds look very similar to each other. Both have three peaks representing the three IR active vibrational modes, which have similar relative intensities between the two spectra. The only difference is that the peaks in the GaBr₃ spectrum are generally less intense than those in the spectrum of BH₃.

In both spectra the A₂" and E' modes lie close in energy, and also the A₁' and E' modes are quite close, but higher in energy than A₂" and E' modes. This is explained by considering that the A₁' and E' modes involve the stretching and shortening of the Ga-Br and B-H bonds, which require a lot of energy (stretching is contrasted by the bond strength, shortening is contrasted by the electron-electron repulsion between the two atoms), while the A₂" and E' modes involve the motion of the ligand atoms around the central atom while the Ga-Br and B-H bond length remains the same, thus less energy is needed for these types of vibration.

It is important to use the same method and basis set for both the optimization and frequency analysis calculations for both molecules in order to be able to compare the relative energies and frequencies. The purpose of performing a frequency analysis is to confirm that the structure of the molecule obtained from the optimization is a minimum. The "Low frequencies" reported in the log file represents the "-6" frequencies of the total 3N-6 vibrational frequencies of a non-linear molecule. These frequencies are the motions (rotation and translation) of the center of mass, which should be much smaller than the first "real" vibrations of the molecule listed. Theoretically, these frequencies are expected to be equal to zero, since we are probing the vibrations of the molecule, rather than the rotation and translation. However, in reality when a molecule is excited to vibrate it also presents some small degree of rotational and translational motion. Thus, in general, the closer these frequencies are to zero, the better the method used. The typical values of "Low frequencies" usually lie in the range of plus/minus 15 cm^-1, which indicate a good level of accuracy of the method used.

Molecular orbitals

BH₃ molecule

File:CB BH3 MOs.txt

DOI:10042/27635

A good match between the computed (quantitative) and the approximate MOs produced via MO diagrams (qualitative) can be observed from the picture above. However, the main difference between the two methods is the representation of the electron density, which is localized on the single atoms in the qualitative MOs, while it is more diffuse in space in the computed MOs. Hence, while the quantitative method shows the regions of the molecule with highest electron density, the qualitative method accounts for the single atoms contribution to the bonding/anti-bonding character of the MO. Therefore, despite the qualitative MOs description is not highly accurate, since it does not coincide with the real picture of the electrons localization in the molecule, it is still a very useful method which allows to predict the MOs relative energies and interactions.

NH₃ molecule analysis

Optimization

File:CB NH3 OPT.txt

• File Name = CB_NH3_OPT
• File Type = .log
• Calculation Type = FOPT
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -56.55776856 a.u. ~ -56.558 a.u.
• RMS Gradient Norm = 0.00000885 a.u.
• Imaginary Freq =
• Dipole Moment = 1.8464 Debye ~ 1.85 Debye
• Point Group = C1
• Job cpu time: 0 days 0 hours 0 minutes 15.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629718D-09
 Optimization completed.
    -- Stationary point found.

Frequency analysis

File:CB NH3 FREQ.txt

• File Name = CB_NH3_FREQ_fine
• File Type = .log
• Calculation Type = FREQ
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -56.55776872 a.u. ~ -56.558 a.u.
• RMS Gradient Norm = 0.00000322 a.u.
• Imaginary Freq = 0
• Dipole Moment = 1.8465 Debye ~ 1.85 Debye
• Point Group = C3
• Job cpu time: 0 days 0 hours 0 minutes 12.0 seconds.

Low frequencies ---   -0.0137   -0.0025    0.0021    7.0781    8.0927    8.0932
Low frequencies --- 1089.3840 1693.9368 1693.9368

MOs analysis

File:CB NH3 MOs.txt

DOI:10042/27637

• File Name = CB_NH3_MOs
• File Type = .log
• Calculation Type = SP
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -56.55776856 a.u. ~ -56.558 a.u.
• RMS Gradient Norm = a.u.
• Imaginary Freq =
• Dipole Moment = 1.8464 Debye ~ 1.85 Debye
• Point Group = C1
• Job cpu time: 0 days 0 hours 0 minutes 31.8 seconds.

NBO analysis

NH₃BH₃ analysis

Optimization

File:CB NH3BH3 OPT.txt

• File Name = CB_NH3BH3_OPT
• File Type = .log
• Calculation Type = FOPT
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -83.22468911 a.u. ~ -83.225 a.u.
• RMS Gradient Norm = 0.00000131 a.u.
• Imaginary Freq =
• Dipole Moment = 5.5647 Debye ~ 5.56 Debye
• Point Group = C1
• Job cpu time: 0 days 0 hours 1 minutes 15.0 seconds.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000026     0.000060     YES
 RMS     Displacement     0.000012     0.000040     YES
 Predicted change in Energy=-9.251712D-11
 Optimization completed.
    -- Stationary point found.

Frequency analysis

File:CB NH3BH3 FREQ.txt

• File Name = CB_NH3BH3_FREQ
• File Type = .log
• Calculation Type = FREQ
• Calculation Method = RB3LYP
• Basis Set = 6-31G(d,p)
• Charge = 0
• Spin = Singlet
• E(RB3LYP) = -83.22468914 a.u. ~ -83.225 a.u.
• RMS Gradient Norm = 0.00000114 a.u.
• Imaginary Freq = 0
• Dipole Moment = 5.5646 Debye ~ 5.56 Debye
• Point Group = C1
• Job cpu time: 0 days 0 hours 0 minutes 34.0 seconds.

Low frequencies ---   -0.0012   -0.0008   -0.0005    2.1701    3.3508    5.2357
Low frequencies ---  263.4767  632.9686  638.4631

NH₃BH₃ association energies

• E(NH₃)= -56.55776856 a.u.
• E(BH₃)= -26.61532360 a.u.
• E(NH₃BH₃)= -83.22468911 a.u.

ΔE=E(NH₃BH₃)-[E(NH₃)+E(BH₃)]=-83.22468911 a.u. a.u. -[−56.55776856 +(−26.61532360)] a.u.= −0.05159695 a.u. ~ −0.052 a.u.

ΔE=−135.46780254 kJmol⁻¹ ~ -135.48 kJmol⁻¹

This appears to be a sensible value since dissociation energies are usually in the range of a few hundreds of kJmol^-1. Furthermore, the value is negative, as expected, demonstrating that the N-B bond formation is a thermodynamically favourable process (i.e. the energy of the product is lower than the sum of the energies of the reagents).