Rep:Mod:catherinelu2

Introduction

In this study, GaussView 5.0 was used to characterise transition structures and calculate reaction energy barriers of the Cope rearrangement and Diels Alder cycloaddition reactions. This was done by molecular orbital-based methods and numerical solutions of the Schrodinger equation to locate energy minima on the potential energy surfaces.

The Cope Rearrangement

The Cope Rearrangement is a pericyclic, [3,3] sigmatropic rearrangement that was discovered by Arthur Cope in 1940 . A 1,5-diene undergoes thermal isomerisation, leading to a thermodynamically more stable regioisomer. In the case of 1,5-hexadiene, the forward and backward reactions are degenerate as the product is identical to the reactant.

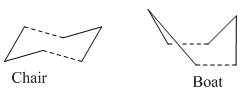
The reaction is believed to proceed via either a chair or a boat transition state, the energies of which were calculated using GaussView.

The objective of this study was to locate the energy minima and transition structures of the C₆H₁₀ potential energy surface in order to determine the preferred reaction mechanism.

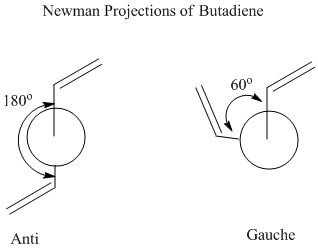
Anti

1,5-hexadiene with an "anti" linkage was drawn in GaussView and optimised: File:ReactantiCL.chk The optimised structure was found to have C2 symmetry.

1,5-hexadiene
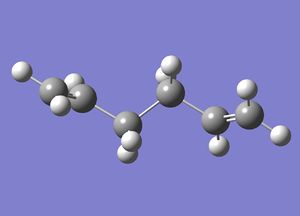
File Type	.chk
Calculation Type	FOPT
Calculation Method	B3YLP
Basis Set	3-21G
Final Energy	-231.69260
Point Group	C2

Gauche

1,5-hexadiene with an "gauche" linkage was drawn in GaussView and optimised (File:ReactgaucheCL.chk); this is expected to be slightly higher in energy than the anti conformation as the hydrogen atoms on each end of the chain are closer together (60 degrees instead of 180 degrees), resulting in increased steric clash.

1,5-hexadiene
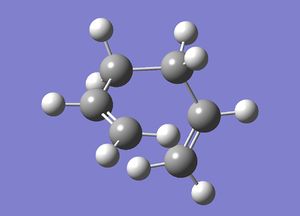
File Type	.chk
Calculation Type	FOPT
Calculation Method	B3YLP
Basis Set	3-21G
Final Energy	-231.68772 a.u.
Point Group	C2

Low-energy conformers of 1,5-hexadiene

The newman projections of the anti and gauche conformations were predicted to be those drawn below:

Based on the above, the low-energy conformers of 1,5-hexadiene were predicted to be used as a reference point for calculating enthalpy and activation energy.

Low-energy conformers of 1,5-hexadiene

Conformer	Structure)	Point Group	Energy/Hartrees HF/3-21G	File
Gauche 1		C2	-231.68772	File:ReactgaucheCL.chk
Gauche 2		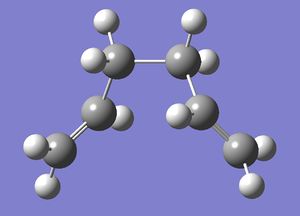C2	-231.69167	File:Reactgauche2CL.chk
Gauche 3		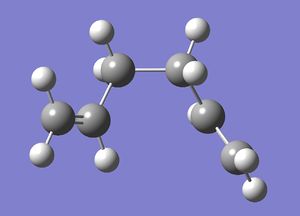C1	-231.69266	File:Reactgauche3CL.chk
Gauche 4		C2	-231.69153	File:Reactgauche4CL.chk
Gauche 5		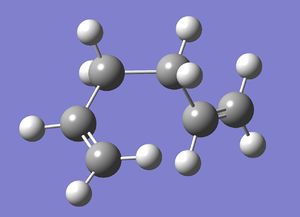C1	-231.68962	File:Reactgauche5CL.chk
Gauche 6		C1	-231.68916	File:Reactgauche6CL.chk
Anti 1		C2	-231.69260	File:ReactantiCL.chk
Anti 2		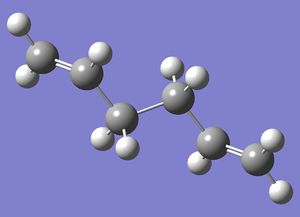Ci	-231.69254	File:Reactanti2CL.chk
Anti 3		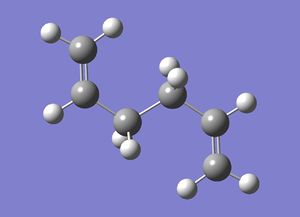C2h	-231.68907	File:Reactanti3CL.chk
Anti 4		C1	-231.69097	File:Reactanti4CL.chk

It can be seen from the calculations above that the lowest energy conformers are Gauche 3, Anti 1 and Anti 2. At this level of theory, the Anti 2 is the lowest in energy as the bulky R groups are anti-periplanar, positioned at the maximum furthest distance possible away from each other, leading to the least steric clash. Gauche 3 is slightly higher in energy than Anti 1 due to the bulky R groups being closer together. The dihedral angle is 60 degrees in gauche as opposed to 180 degrees in anti. Anti 2 is also slightly higher in energy than Anti 1, as the R groups are eclipsed in Anti 2.

C_i anti 2 conformation of 1,5-hexadiene

The lowest energy conformer was then optimised at a higher level of theory to ensure the accuracy of these calculations. The energy calculated File:AntiCiCL.chk at the HF/321G level was identical to that of appendix 1 to 5 decimal places. The symmetry was C_i.

1,5-hexadiene
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-234.69254
Point Group	Ci

Sum of electronic and zero-point Energies=           -231.539539
 Sum of electronic and thermal Energies=              -231.532565
 Sum of electronic and thermal Enthalpies=            -231.531621
 Sum of electronic and thermal Free Energies=         -231.570916

Optimisation at the DFT/6-31G level

1,5-hexadiene
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3YLP
Basis Set	6-31G(D)
Final Energy	-234.61172
Point Group	Ci

Sum of electronic and zero-point Energies=           -234.469217
 Sum of electronic and thermal Energies=              -234.461857
 Sum of electronic and thermal Enthalpies=            -234.460913
 Sum of electronic and thermal Free Energies=         -234.500849

The final symmetry is unchanged at C_i; the energy is slightly less negative than that calculated by HF/3-21G. This is slightly more negative than the literature value of -234.32879 .

Frequency Analysis

Frequency analysis was used to characterize the critical point and to confirm that it is a minimum on the potential energy surface, by checking that all vibrational frequencies are real and positive. This was carried out using the DFT/B3LYP method.

File:ANTICICLFREQ.LOG

Low frequencies ---  -11.5689   -0.0004   -0.0002    0.0007    9.3727   20.5035
 Low frequencies ---   72.6804   77.6552  120.6709

1,5-hexadiene
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3YLP
Basis Set	6-31G(D)
Final Energy	-234.61172
Point Group	Ci

The frequency analysis yielded the thermochemistry data.

Potential energy at 0K = E_elec + Zero Point Energy = -234.469217

Energy at 298.15 K and 1 atm of pressure, including translational, rotational, and vibrational energy modes = E + E_vib + E_rot + E_trans = -234.461857

Enthalpy H = E + RT = Sum of electronic and thermal enthalpies = -234.460913

Free energy G = H - TS = Sum of electronic and thermal free energies = -234.500849

The activation energy is calculated by E_a = H_product - H_reactant.

Optimizing the Chair and Boat Transition Structures of the Cope Rearrangement

Chair

The transition state of the Cope Rearrangement was optimised by two different methods. First, the Hartree-Fock with 3-21G basis set was used; the results obtained were compared to those obtained by freezing the reaction coordinate.

It is more difficult to optimise a transition state, as it is necessary to know the negative direction of the curvature of the potential energy surface. One of the difficulties found in attempting this was that if the transition state was not guessed to a sufficient accuracy, upon optimisation, the reaction would be seen to proceed in the wrong direction resulting in the constituent molecules separating from the transition state into separate reactant molecules.

If the geometry of the transition state is known to a reasonable accuracy, the force constant may be easily computed in the optimisation, which is updated as the calculation proceeds. If the transition state geometry is not known accurately, the curvature of the potential energy surface may be dramatically different at points that are far away from the transition structure, in which case a better transition structure is found by freezing the reaction coordinate, minimising the rest of the molecule, unfreezing the reaction coordinate and then optimising the transition state.

Hartree-Fock

An allyl fragment was optimised at the HF/3-21G level of theory; two of these optimised fragments were then placed one on top of the other at approximately 2.2 angstroms apart, as an approximate chair transition state. A sufficiently accurate transition state guess is required for the transition state to be successfully charaacterised. This guessed transition state was then optimised using HF/3-21G, with force constants calculated once and optimised to a Berny transition state. [1]

Chair Transition State
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.61932

Sum of electronic and zero-point Energies=           -231.466700
 Sum of electronic and thermal Energies=              -231.461341
 Sum of electronic and thermal Enthalpies=            -231.460397
 Sum of electronic and thermal Free Energies=         -231.495206

The frequency calculation gave an imaginary frequency of magnitude 818 cm^-1, corresponding to the vibration depicting the Cope Rearrangement. The keyword 'Opt=NoEigen' in the optimisation ensured that the calculation proceeded in the event that there were more than 2 imaginary frequencies obtained.

The distance between the C atoms that are to form new C-C bonds is 2.020.

Frozen Coordinate Method

The guessed chair transition state was also optimised using the frozen coordinate method, where the 2 C-C bonds that are to be formed are frozen to a distance of 2.2Å apart. The rest of the molecule was optimised to a minimum with a QST2 method.

The resultant system resembled the input molecule in geometry but the 2 C-C bonds to be formed were fixed at a distance of 2.2Å. These bonds were unfrozen. The Hessian force constant matrix was computed by setting the C atoms that are to form bonds to 'derivative' in order to calculate the second derivatives of the potential energy surface, i.e. the force constants. This was then optimised using HF/3-21G to a Berny transition state (force constants never computed). File:ChairtsderivCL.chk

Cope Rearrangement
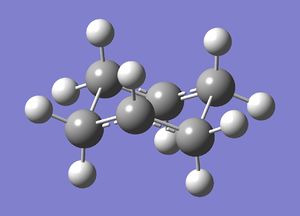
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.61932

The resultant transition state is of the same geometry as that previously obtained. The newly formed C-C bonds have a length of 2.02190, an increase from that predicted by the Hartree-Fock calculation.

Boat

The boat transition structure was optimised using the QST2 method, where the reactants and products are specified and the calculation interpolates between the two structures to find the transition state in between.

Initially, the optimised anti2 structure was used as the input - this failed File:Boatqst2failCL.chk. This was because the guessed transition state was too dissimilar from the real transition state, so the calculation only translated the top allyl fragment; there was no rotation around the central bonds. The QST2 method is therefore unsuitable for locating the boat transition structure using these reactant and product structures.

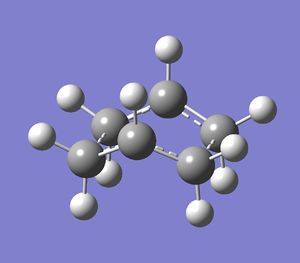
To solve this, the central dihedral angle was set to 0 degrees and each inside C-C-C bond angle was set to 100 degrees for both reactant and product, making the guessed transition state a more accurate replica of the real transition state. This was optimised using the same method, yielding the boat transition structure.

File:Boatqst2CL.chk

Cope Rearrangement
File Type	.chk
Calculation Type	FREQ
Calculation Method	B3lYP
Basis Set	6-31G(D)
Final Energy	-231.60280

The newly formed C-C bonds were of length 2.14 angstroms.

Sum of electronic and zero-point Energies=           -234.402342
 Sum of electronic and thermal Energies=              -234.396008
 Sum of electronic and thermal Enthalpies=            -234.395063
 Sum of electronic and thermal Free Energies=         -234.431753

The frequency calculation gave a single imaginary frequency of magnitude 840 cm^-1:

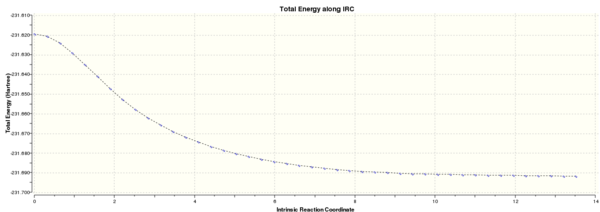
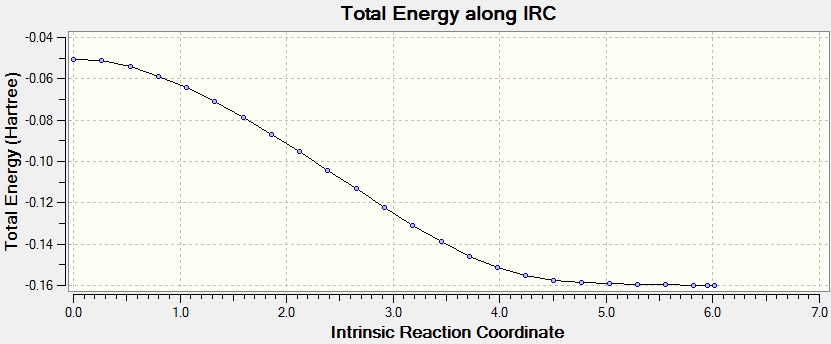
Intrinsic Reaction Coordinate

The IRC is the minimum energy reaction pathway between a reaction's transition state and the reactants/products in mass-weighted cartesian coordinates. The IRC method enables the identification of the conformer to which a specific transition structure leads, by following the minimum energy path from a transition state down to its local minimum on the potential energy surface. This is done by taking small steps towards the part of the energy surface where the gradient is steepest.

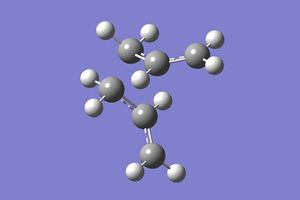
The direction of the IRC path can be chosen as forwards, backwards or both ways. The optimised chair transition state was used to compute the forward reaction only, as for the purposes of this particular reaction, the forward and backward reactions are symmetrical. The force constants were set to 'calculate always' and the number of points computed along the IRC was set to 50. [2]

Cope Rearrangement
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.69158

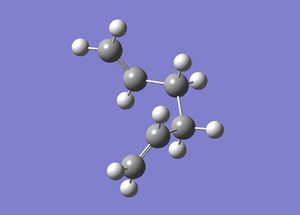
The IRC was found to have not yet reached a minimum geometry. The job was rerun with the new setting of computing 100 points along the IRC [3] instead of 50 and then the resultant structure was optimised [4], which resembled the gauche 2 conformer:

Cope Rearrangement
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Final Energy	-234.61069

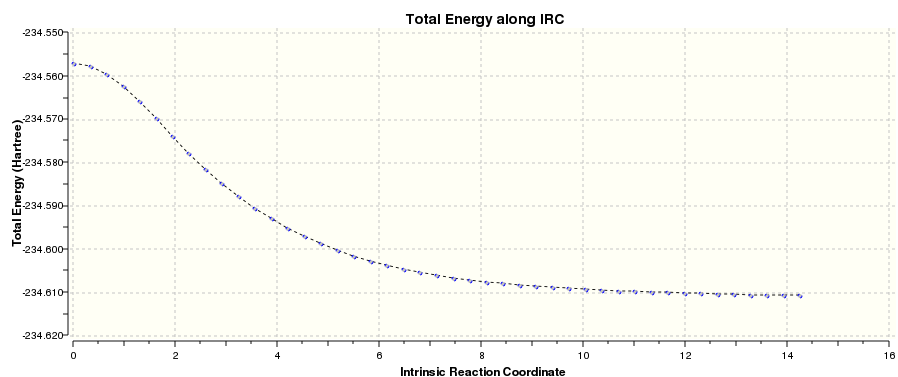
The IRC energy plot showed the total energy of the system approaching a minimum as the gradient of the potential energy plot approached zero when 100 points were plotted:

B3LYP/6-31G* Optimisations

The chair and boat transition states were then optimised at a higher level of theory.

Chair

The chair optimisation: [5]

Chair
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Final Energy	-234.55698

Sum of electronic and zero-point Energies=           -234.414929
 Sum of electronic and thermal Energies=              -234.409008
 Sum of electronic and thermal Enthalpies=            -234.408064
 Sum of electronic and thermal Free Energies=         -234.443814

An IRC calculation was run with a B3LYP/6-31G* method [6]. From this, the activation energy at this level of theory could be calculated.

The activation energy was calculated to be 33.66 kcal/mol.

Boat

The boat optimisation: [7]

Boat
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Final Energy	-234.54309

Sum of electronic and zero-point Energies=           -234.402342
 Sum of electronic and thermal Energies=              -234.396008
 Sum of electronic and thermal Enthalpies=            -234.395063
 Sum of electronic and thermal Free Energies=         -234.431753

An IRC calculation was run with a B3LYP/6-31G* method and 100 points calculated along the IRC [8]. From this, the activation energy at this level of theory could be calculated.

The activation energy was calculated as - 37.64 kcal/mol.

As seen above, the IRC had not yet reached a minimum geometry. The final structure was taken and optimised to a minimum using the B3LYP/6-31G* method.

Energies Summary and Activation Energy

Below is a summary of calculated values at 298K and also reported values for 0K and experimentally determined values [9] in italics.

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.46671	-231.46134	-234.55698	-234.41492	-234.40901
Boat TS	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
Reactant (anti2)	-234.69254	-231.53954	-231.53257	-234.61172	-234.46920	-234.46186

Activation energies/kcal mol^-1

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K
ΔE (Chair)	45.70	45.34	34.06	33.66	33.5 ± 0.5
ΔE (Boat)	55.60	50.31	41.96	37.64	44.7 ± 2.0

It can be seen from the values above that at both levels of theory, the boat transition state is higher in energy than the chair transition state. The B3LYP/6-31G(d) method gives activation energies that are much closer to those determined experimentally than the HF/3-21G method for both chair and boat. In particular, the chair transition state calculated at 0K using B3LYP/6-31G(d)gives a value that is within the error range of the experimentally determined value, showing the power and accuracy of computational methods.

For all values, the sum of electronic and zero-point energies at 0K is more negative than the sum of electronic and thermal energies at 298K; this is to be expected as the thermal energy is a positive value.

The Diels-Alder Cycloaddition

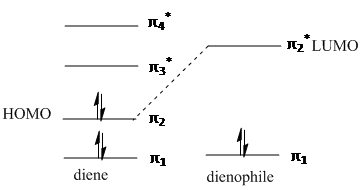
The Diels-Alder is a pericyclic, thermal, π4s + π2s cycloaddition between a conjugated s-cis diene and a dienophile. The reaction occurs via a single transition state as is characteristic of a pericyclic concerted reaction. Orbitals of the same symmetry combine via a six centred transition state, forming two σ bonds and one new π bond in the product. For a successful reaction to occur, the diene must be in the s-cis conformation, so that the ends of the diene can favourably overlap and interact with the ends of the pi system of the dienophile:

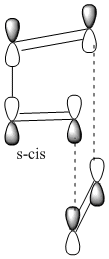
The dienophile preferably has an electron withdrawing group conjugated to the alkene, making the pi bond electron deficient. This makes the diene HOMO and dienophile LUMO closer together in energy and the donor-acceptor interation stronger, leading to a faster reaction rate.

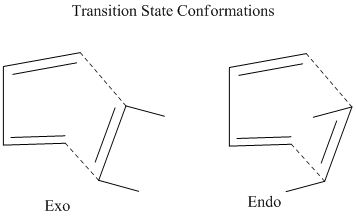
These substituents can be exo or endo to the cyclic diene system.

Butadiene

Cis-butadiene was optimised using an AM1 semi-empirical molecular orbital method: File:BUTADIENEOPTCL.LOG

Butadiene
File Type	.log
Calculation Type	FOPT
Calculation Method	RAM1
Basis Set	ZDO
Energy	0.048797

Butadiene is symmetric with respect to the plane.

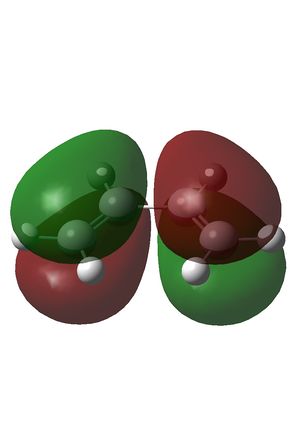
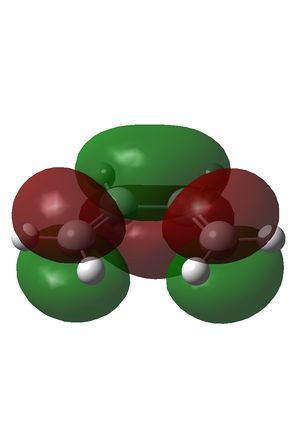
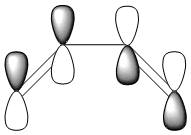
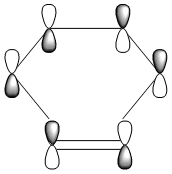
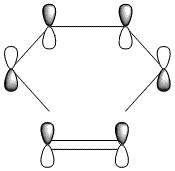
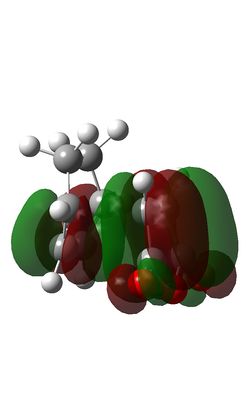
The HOMO and LUMO were also plotted and the LCAOs inferred from these. The HOMO is antisymmetric and the LUMO symmetric with respect to the plane. As the reaction is between the antisymmetric butadiene HOMO and the antisymmetric ethene LUMO, this reaction is allowed.

HOMO	LUMO
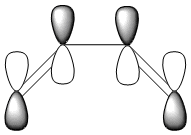AS	S

Diels Alder

An envelope transition state was formed in GaussView that maximised the overlap between the ethylene π orbitals and the π system of butadiene. The distance between the C atoms that were to form new C-C sigma bonds was set at 2.2 angstroms; this was then optimised to a Berny transition state with force constants calculated once. This structure was then optimised using the semi-empirical AM1 method [10]:

Diels-Alder Transition State
File Type	.chk
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Energy	0.111655

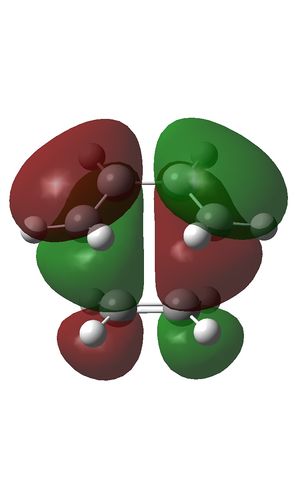
There was one imaginary vibrational mode at -956.07cm^-1, corresponding to the symmetrical bending motion of the C atoms that are to form the C-C bonds. The motion shows that the formation of the two C-C bonds is synchronous.

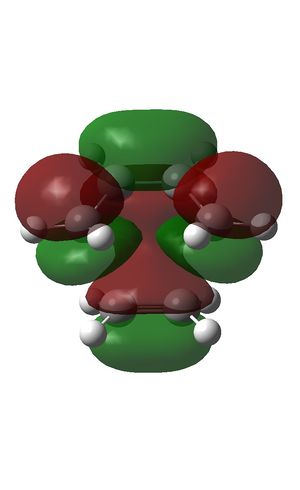
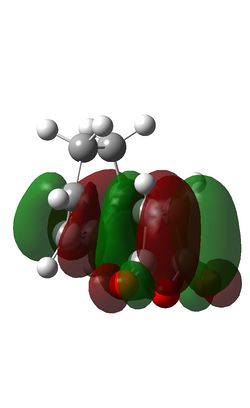
The HOMO (left) and LUMO (right) were plotted and the LCAOs inferred:

HOMO	LUMO
AS	S

The partially formed sp³ σ C-C bonds formed by C=C bond breaking of ethene had a length of 1.3829; the partially formed sp² bond of cyclohexene had a length of 1.3975 (see below; literature values in brackets). This compares to a normal C=C bond length of 1.3305 angstroms in ethene and a C-C bond length of 1.454 A in butadiene . The bond lengths calculated are intermediate between a conventional sp² and sp³ bond, indicating some degree of aromaticity and delocalised pi electron density in the transition state. The bonds in the process of forming and breaking are of similar lengths, which alludes to the identical bond lengths characteristic of aromatic systems. This also indicates that the bond breaking and bond forming occurs at the same time; this is consistent with a concerted cyclic transition state.

The HOMO was formed from the HOMO of butadiene and the LUMO of ethene. The transition state is antisymmetric as expected from formation by LCAO of the antisymmetric diene HOMO and antisymmetric dienophile LUMO, thus preserving the orbital symmetry in the product and obeying the Woodward-Hoffman orbital symmetry rules .

Regioselectivity of the Diels-Alder Reaction

Where the diene is cyclic, such as in the reaction of maleic anhydride with cyclopentadiene, the endo isomer is formed as the major product in a product ratio of 99:1 .

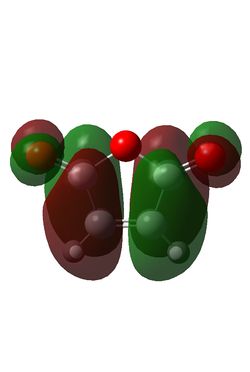
Maleic anhydride and cyclohexadiene were initially optimised using the semi-empirical/AM1 method: File:MaleicanhydrideoptCLam1.chk File:Hexadieneam1CL.chk. This yielded the following MOs:

Maleic Anhydride HOMO	Maleic Anhydride LUMO	Cyclohexadiene HOMO	Cyclohexadiene LUMO
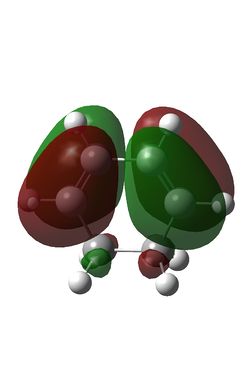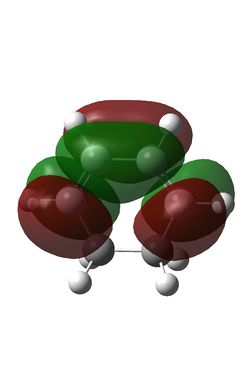
S	AS	AS	S

The reaction is between the diene HOMO (AS) and the dienophile LUMO (AS); conservation of orbital symmetry rules means the product will also be antisymmetric .

Endo

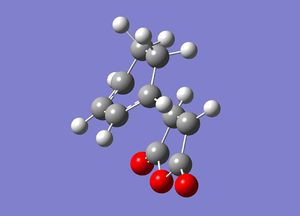
First the transition state of the reaction leading to the endo product was guessed. The bond coordinates of the 4 C atoms to form the new C-C bonds were frozen and set to 2.2 angstroms apart. This was then optimised initially to a minimum: [11]

The bond coordinates were then unfrozen and the Hessian force constant matrix was then computed to find the reaction transition state. [12]

Endo
File Type	.chk
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Energy	-0.051505

The transition state had one imaginary vibrational frequency at -806.17 cm^-1 corresponding to the formation of the two new C-C sigma bonds.

The IRC with a semi-empirical/AM1 method and 100 points calculated along the IRC and activation energy were also calculated [13]:

The activation energy was calculated to be 68.70 kcal/mol.

The final structure was seen to be formed in the course of the IRC; the C=C pi bond of maleic anhydride becomes a C-C sigma bond; the 2 C=C bonds of butadiene also form C-C bonds and the C-C bond in between these forms a C=C bond.

Exo

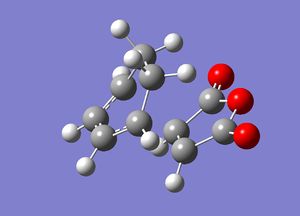
The above was repeated for the reaction leading to the exo transition state. The guessed transition state was first optimised to a minimum by the frozen coordinate method [14]] and then optimised to a transition state by unfreezing the coordinates and computing the Hessian force constant matrix [15] leading to the exo product:

Exo
File Type	.chk
Calculation Type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Energy	-0.05042

The resultant transition state had one imaginary vibrational frequency at -811.20 cm^-1 from a symmetric bend, corresponding to the concerted formation of the 2 new C-C sigma bonds.

The IRC with a semi-empirical/AM1 method and 100 points calculated along the IRC and activation energy were also calculated [16]:

The activation energy was calculated to be 68.19 kcal/mol, lower than that of the exo transition state.

The final structure was seen with concerted bond formation in the course of the IRC; the C=C pi bond of maleic anhydride becomes a C-C sigma bond; the 2 C=C bonds of butadiene also form C-C bonds and the C-C bond in between these forms a C=C bond:

Secondary Orbital Overlap

The Diels-Alder reaction between maleic anhydride and cyclohexadiene takes place thermally with 4n+2 (n=1) electrons moving suprafacially. Both the HOMO of cyclohexadiene and LUMo of maleic anhydride are antisymmetric, meaning the reaction is allowed and the resultant MOs are also antisymmetric.

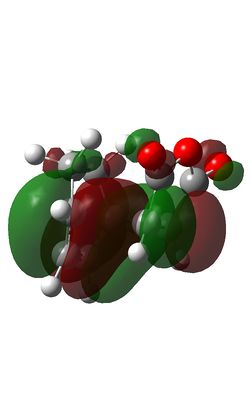
Endo HOMO	Endo LUMO	Exo HOMO	Exo LUMO

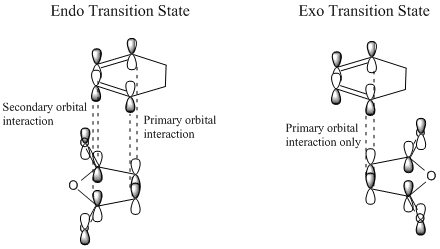
The steric congestion of the endo form can be seem in the above HOMO of the transition state; the downwards-pointing antibonding π* of the terminal oxygen atoms on maleic anhydride clash with the antibonding π* orbitals of the C=C bonds in cyclohexadiene. In the exo form, the oxygen π* orbitals are orientated upwards, away from the π* C=C orbitals, reducing the unfavourable repulsions and giving the endo product the lowest free energy.

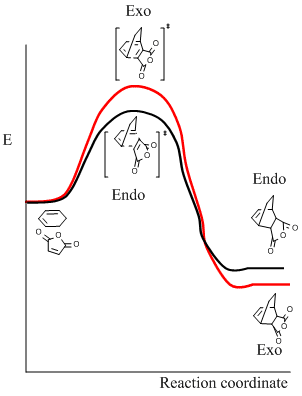
It can be seen that the exo transition state is of slightly higher energy (-0.05042) than the endo transition state (-0.05151), evidenced in the IRC calculations above, but the exo product is lower in energy than the endo product due to steric congestion in the endo form. The reaction is under kinetic control meaning the thermodynamically less stable product with the lower energy transition state, i.e. the endo form, predominates.

The ratio of product conformers may be rationalised by the respective transition states. The endo product is formed from the lowest energy transition state, where the dienophile tends to be orientated directly above the partially unsaturated diene. This stabilises the endo transition state due to spacial orbital overlap and also has the least destabilisation by steric repulsion, giving the endo transition state the lowest free energy, meaning the kinetic endo product predominates.

In the endo transition state, it can be seen that the orbitals of the carbonyl groups of maleic anhydride are of the correct symmetry and alignment to stabilise the HOMO orbitals of cyclohexadiene. This interaction is not possible in the exo transition state, making the endo transition state of lower energy .

Conclusions

Using semi-empirical AM1 methods, it has been demonstrated that the Diels-Alder reaction proceeds by the AS diene HOMO and AS dienophile LUMO, resulting in a product with conservation of orbital symmetry. the regiochemistry of the Diels Alder reaction was shown for the reaction between maleic anhydride and cyclohexadiene, where the endo product was overwhelmingly the major product despite being more sterically congested and of higher energy than the exo product. The reasons for this were rationalised by frontier molecular orbital theory.

References

<references>