Rep:Mod:cai2018
BH3
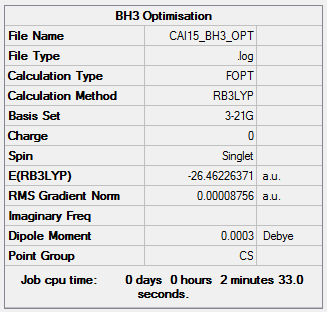
BH3 was optimised initially using a low-level B3LYP/3-21G level mode of optimisation, followed by a higher power B3LYP/6-31G level mode.
B3LYP/3-21G Level
Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000441 0.001200 YES
B3LYP/6-31G Level
At the 6-31G level, an additional frequency analysis was also carried out.
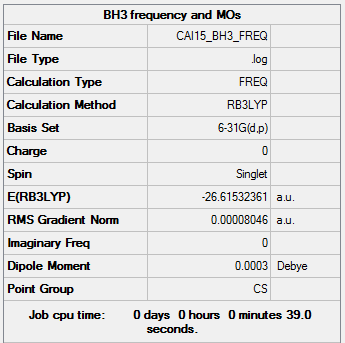
Item Value Threshold Converged? Maximum Force 0.000185 0.000450 YES RMS Force 0.000080 0.000300 YES Maximum Displacement 0.000770 0.001800 YES RMS Displacement 0.000312 0.001200 YES
Low frequencies --- 0.0006 0.0007 0.0009 33.2756 41.6973 43.2405 Low frequencies --- 1163.4847 1213.4680 1213.6222
BH Molecule |
Vibrational Spectrum for BH3
The six vibrational modes for BH3 are shown in the table below:
| Wavenumber (cm-1 | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 1163 | 92 | A1 | yes | out of plane bend |
| 1213 | 14 | E | very slight | bend |
| 1213 | 14 | E | very slight | bend |
| 2580 | 0 | A1 | no | symmetric stretch |
| 2713 | 126 | E | yes | asymmetric stretch |
| 2714 | 126 | E | yes | asymmetric stretch |
The computer-generated IR spectrum for BH3 is shown below:
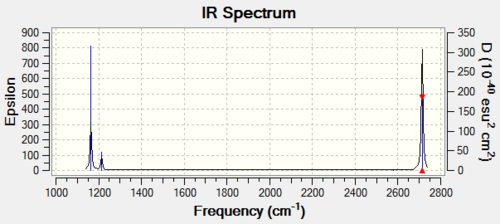
BH3 is a four atom, non-planar molecule, and thus from the equation 3N-6, is expected to have six vibrational modes. These six vibrational modes are described in the table above. However, only three vibrational peaks appear in the IR spectrum. Vibrations with E symmetry are doubly degenerate, and thus the two vibrational modes will overlap to show one peak in the spectrum. This is the case for the in-plane bend pair at 1213 cm-1 and the asymmetric stretch pair at 2713/2714 cm-1 (the slight frequency discrepency in the second pair is likely due to slight energy miscalculations). The fourth vibrational mode (symmetric stretch) does not have a strong enough intensity to be seen in the spectrum. This leads to three peaks shown in the IR spectrum.
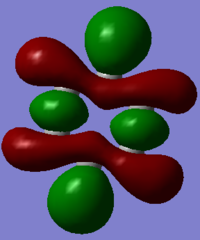
Molecular Orbital Diagram
The molecular orbital diagram for BH3 is shown below, with the eight lowest energy computed MOs added.
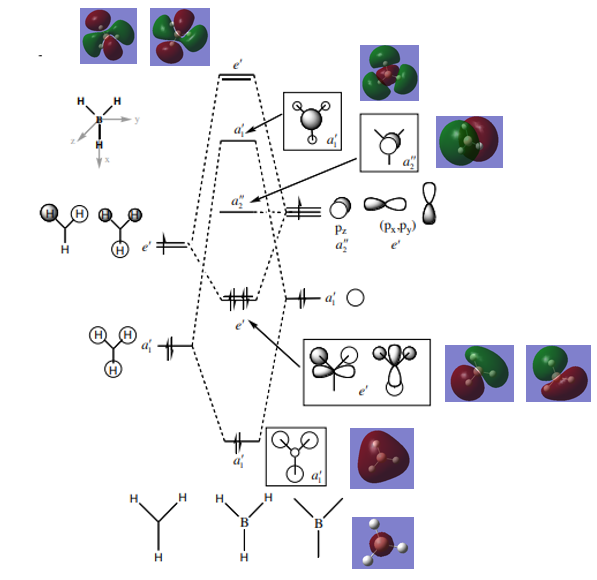
There are no significant differences between the real and LCAO MOs, and thus qualitative MO theory can be considered relatively accurate.
Smf115 (talk) 16:58, 28 May 2018 (BST)Good inclusion of the MOs in the diagram however, some seem to be repeats (such as the top two e' MOs) and not the two unique orbitals. The useful nature of qualitative MO theory is highlighted but to improve, the differences in the AO contributions for some of the MOs, such as the 3a1' MO, could have been noticed.
NH3
B3LYP/6-31G Level
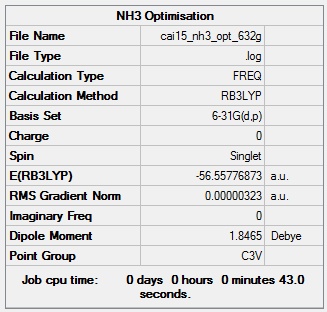
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
Low frequencies --- -0.0128 -0.0017 0.0008 7.1034 8.1048 8.1051 Low frequencies --- 1089.3834 1693.9368 1693.9368
NH Molecule |
NH3BH3
B3LYP/6-31G Level
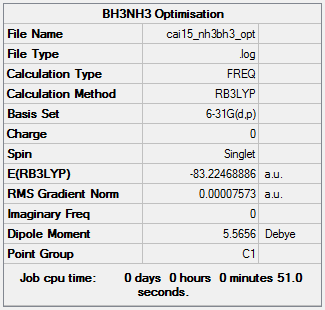
Item Value Threshold Converged? Maximum Force 0.000159 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000511 0.001800 YES RMS Displacement 0.000237 0.001200 YES
Low frequencies --- -0.0011 0.0006 0.0009 11.2475 11.8336 28.3139 Low frequencies --- 264.0265 633.0284 638.5234
NHBH Molecule |
Calulation of B-N Bond Energy
The energy of the dative B-N bond was calculated using the optimised energies of BH3, NH3 and NH3BH3:
E(BH3)=-26.61532350 a.u.
E(NH3)=-56.55776873 a.u.
E(NH3BH3)=-83.22468886 a.u.
ΔE=E(NH3BH3)-[E(BH3+E(NH3)]
ΔE=(-83.22468886)-(-26.61532350+(-56.55776873))
ΔE=-0.05159663 a.u.
1 a.u. = 1 Hartree = 2625.50 kJ mol-1 [2]
ΔE=(-0.05159663)*(2625.50)
ΔE=-135 kJ mol-1 (±10 kJ mol-1)
The N-B dative bond energy is comparable to the strength of an O-O single bond (-145 kJ mol-1)[3], which is generally considered a weak bond. The N-B bond energy is even smaller than the O-O bond energy, and thus itself can be considered a weak bond.
Smf115 (talk) 16:56, 28 May 2018 (BST)Good comparison made with a referenced literature value, correct calculation and consideration given to the accuracy of the final energy value in kJ/mol.
BBr3
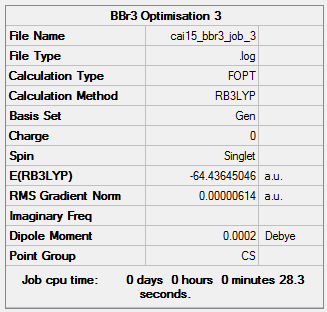
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000045 0.001800 YES RMS Displacement 0.000032 0.001200 YES
Low frequencies --- -1.9018 -0.0002 -0.0002 -0.0002 1.5796 3.2831 Low frequencies --- 155.9053 155.9625 267.7047
D-Space link: http://hdl.handle.net/10042/202471
DOI: 10042/202471
BBr Molecule |
Aromaticity Project
Benzene Optimisation
Item Value Threshold Converged? Maximum Force 0.000193 0.000450 YES RMS Force 0.000094 0.000300 YES Maximum Displacement 0.000799 0.001800 YES RMS Displacement 0.000367 0.001200 YES
Low frequencies --- -11.6655 -0.0007 -0.0007 0.0006 5.1881 15.0078 Low frequencies --- 414.0175 414.6060 621.0759
Benzene |
Borazine Optimisation
Item Value Threshold Converged? Maximum Force 0.000201 0.000450 YES RMS Force 0.000067 0.000300 YES Maximum Displacement 0.000349 0.001800 YES RMS Displacement 0.000120 0.001200 YES
File:CAI15 NEW BORAZINE FREQ.LOG
Low frequencies --- -10.6718 -0.0008 -0.0004 -0.0001 9.9404 11.3052 Low frequencies --- 288.5908 290.4328 404.2362
Borazine |
Benzene vs Borazine
Charge Comparison
| Borazine | Benzene |
|---|---|
|
|
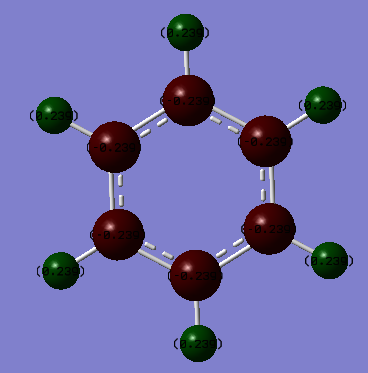
In borazine the relative NBO charges on each atom are:
Boron = 0.747
Nitrogen = -1.102
Hydrogen (B-H) = -0.077
Hydrogen (N-H) = 0.432
In benzene the relative NBO charges on each atom are:
Carbon = -0.239
Hydrogen = 0.239
The electronegativities of the relevant atoms are[4]:
Boron = 2.04
Carbon = 2.55
Nitrogen = 3.04
Hydrogen = 2.20
There is a slight electronegativity difference between carbon (2.55) and hydrogen (2.20) of 0.35. The C-H bonds in benzene are expected to be slightly polarised covalent, with the carbon negative in relation to the hydrogen, due to the slightly stronger pull of the electrons. This is shown by the relative NBO charges that are calculated, as carbon is -0.239 and hydrogen is +0.239.
In borazine, the situation is slightly more complicated, due to the ring containing two different atoms (nitrogen and boron, rather than just carbon as in benzene). Boron (2.04) is slightly less electronegative than hydrogen (2.20), whereas nitrogen (3.04) is slightly more electronegative than hydrogen. The B-H covalent bonds are expected to be polarised towards the hydrogen, with the boron positively charged with respect to hydrogen, due to a small electronegativity difference of 0.16. The N-H covalent bonds are expected to have a greater degree of polarisation, in this case towards the nitrogen atom, with the nitrogen atom negatively charged with respect to the hydrogen, due to an electronegativity difference of 0.84. However, the electronegativity difference between boron and nitrogen must also be considered for the N-B bonds in the ring. The electronegativity difference for nitrogen and boron is 1.00, and thus these bonds are expected to be polarised towards nitrogen, with the nitrogen atoms negatively charged with respect to boron. This accents the polarity of the B-H and N-H bonds, leading to the nitrogen atoms being relatively strongly negatively charged (-1.102) and the boron atoms being slightly more positively charged (+0.747) in comparison to the B-H hydrogens (-0.077) and N-H hydrogens (+0.432).
The high symmetry of benzene (D6h) is reflected in the symmetrical charge distribution between all atoms. The introduction of alternating atoms in borazine lowers the symmetry (D3h) and introduces a dependency of charge based on neighbouring atoms, with alternating positive and negative hydrogens. Overall, the atoms in borazine are more highly charged than in benzene, due to greater electronegativity differences between atoms.
Smf115 (talk) 14:56, 1 June 2018 (BST)Great charge analysis with the same colour range used across both molecules to highlight the charge distribution and a detailed justification of the charges by both electronegativities and symmetry.
MO Comparison
| Borazine | Benzene | Comparison |
|---|---|---|
 |
 |
Benzene MO15 and borazine MO14 are both relatively high energy sigma bonding MOs. The MOs are totally bonding as the nodal planes lie on the atoms and not between the bonds, however the presence of the six nodes in both MOs does lead to the relatively high energy. The benzene MO is totally symmetric, with the orbitals lying equidistance from each hydrogen atom. In the borazine MO, the orbitals lie slightly towards the N-H hydrogen atoms, which carry a slight positive charge, and slightly further from the essentially neutral B-H hydrogens, due to differing orbital contributions from the boron and nitrogen atoms. |
 |
 |
Benzene MO19 and borazine MO19 are both sigma anti-bonding orbitals. The benzene MO is symmetric due to equivalence of all the carbon and hydrogen atoms. In borazine, the boron and nitrogen atoms contribute differently to the MO. Boron is higher in energy than nitrogen, and thus contributes more, leading to a greater coefficient from the boron orbitals, distorting the MO towards the boron atom. |
 |
 |
Benzene MO21 and borazine MO21 are both pi bonding MOs. The benzene MO is symmetric due to the equivalence of the carbon and hydrogen atoms. In borazine, the MO is distorted due to differing contributions from the boron and nitrogen atoms, due to different energies of the boron and nitrogen atoms. |
Aromaticity
Aromatic compounds have unusual stability/un-reactivity for unsaturated hydrocarbons.
The concept of aromaticity was first developed for benzene by Kekule in 1865, and worked for compounds containing benzene rings. Molecular orbital theory is based on the linear combination of atomic orbitals. MO theory predicts that benzene consists of a sigma-bonding frameowrk formed from sp2 hybridised carbons, leaving an empty p-orbital on each carbon atom orthogonal to the ring. The six atomic p-orbitals then combine to form six molecular orbitals, which leads to a delocalised pi-system. However, the idea of sp2 orbitals overlapping breaks down for more complicated systems. The extension of Kekule's idea to molecules with chemical reactivities similar to benzene by Erlenmeyer in 1866 lead to the acceptance that all unsaturated systems with cyclic conjugation were aromatic. This in turn was broken down by Willstaetter in 1905 through the synthesis of cyclooctatetraenes, that did not demonstrate the predicted aromaticity[5], thus conjugated systems are not necessarily aromatic.
Huckel's rule was developed in 1931 as an empirical rule for aromaticity. To be aromatic, Huckel stated that a molecule must be:
1. Cyclic.
2. Have a p-orbital on each ring atom.
3. Planar.
For compounds which are planar and have a contiguous, cyclic array of p-orbitals perpendicular to the plane of the ring, those with (4n+2) p-electrons display special stabilisation, and are aromatic. Those with (4n) p-electrons, display special instability, and are anti-aromatic.
The (4n+2) rule does not work for all molecules - pyrene and coronene are examples of aromatic molecules that break this rule.
A recent debate has also been going on as to whether sigma-orbitals also contribute to aromaticity, rather than just a delocalised p-system[6].
By the 1960s, Huckel's rules were expanded, and most chemists accepted that planar, cyclic, delocalised p-electron systems are aromatic, and would show the following ground state properties[7]:
1. Greater stability than the olefinic analogues by an amount known as the 'resonance energy'.
2. Bonds lengths would be equal in the ring, with distances intermediate between those of typical single and double bonds.
3. Show a p-electron ring current induced by an external magnetic field, increasing the diamagnetic susceptibility.
Additionally:
4. Aromatic compounds undergo substitution reactions far more easily than addition reactions (where aromaticity is lost).
Smf115 (talk) 14:55, 1 June 2018 (BST)A very clear discussion of the concepts of aromaticity from the basic concepts up to a more updated criteria with appropriate references. To improve, reference to the MOs just visualised to illustrate why overlapping pZ AOs are a bad descriptor of aromaticity could be made.
Smf115 (talk) 14:55, 1 June 2018 (BST)Overall, a very clear and well presented report.
- ↑ Hunt, P. 'Lecture 4 Tutorial MO Diagram BH3 [1]
- ↑ Constants and Conversion Units [2] 2018, accessed: 22/05/18
- ↑ Chung C., University of Waterloo [3] 2018, accessed 24/05/18
- ↑ Wikipedia, [4], 2018, accessed: 25/05/18
- ↑ T. M. Krygowski et al. / Tetrahedron 56 (2000) 1783–1796
- ↑ Palusiak, M. and Krygowski, T. (2007), Application of AIM Parameters at Ring Critical Points for Estimation of π‐Electron Delocalization in Six‐Membered Aromatic and Quasi‐Aromatic Rings. Chemistry – A European Journal, 13: 7996-8006. doi:10.1002/chem.200700250
- ↑ T. M. Krygowski et al. / Tetrahedron 56 (2000) 1783–1796