Rep:Mod:by416
BH3 Molecule
Method:B3LYP
Basis set:6-21G (d,p)
Item Value Threshold Converged? Maximum Force 0.000070 0.000450 YES RMS Force 0.000039 0.000300 YES Maximum Displacement 0.000356 0.001800 YES RMS Displacement 0.000214 0.001200 YES
Media: File:BY416 BH3 FREQ.LOG
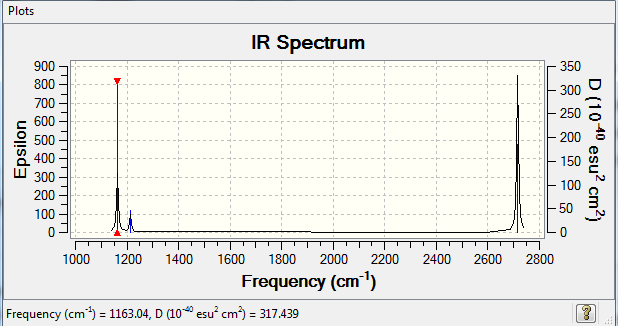
Low frequencies --- -0.6727 -0.3834 -0.0055 12.9097 16.4795 16.4932 Low frequencies --- 1163.0392 1213.2115 1213.2142
BH3 |
IR
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1164 | 92 | A2" | yes | out-of-plane bend |
| 1214 | 14 | E' | slight | bend |
| 1214 | 14 | E' | slight | bend |
| 2580 | 0 | A1' | no | symmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
There are 6 vibrations of BH3, as seen in the table. These do not show up in the IR spectrum because there are two pairs which are degenerate (of the same energy). These degenerate pairs are only seen once in the IR spectrum. Furthermore, for a vibration to be IR active it must have a change in the dipole moment. The A1 symmetric stretch does not invlve an overall change in the dipole moment. Therefore it is not seen in the IR spectrum.
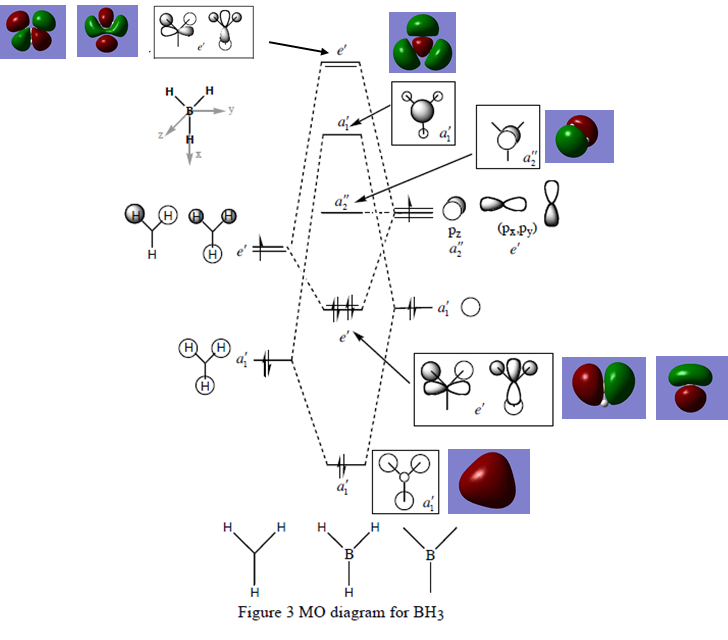
MO diagram
(MO diagram for BH3, Lecture 4 Tutorial Problem Model Answers, P. Hunt, [1], accessed 22/05/18)
The LCAO AOs are similar to the computed MOs. There are areas of electron density and no electron density (nodes) seen in both. This shows that qualitative MO theory is useful as its accuracy is high.
Ng611 (talk) 19:17, 4 June 2018 (BST) Ate there any differences at all that you can see (there actually are some!). Otherwise, good analysis.
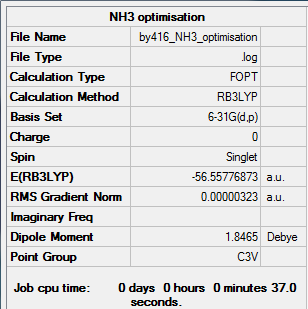
NH3 Molecule
Method:B3LYP
Basis set:6-21G (d,p)
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Media: File:BY416 NH3 OPTIMISATION.LOG
Ng611 (talk) 19:18, 4 June 2018 (BST) This should be a frequency log file here.
Low frequencies --- -8.5646 -8.5588 -0.0044 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
NH3 molecule |
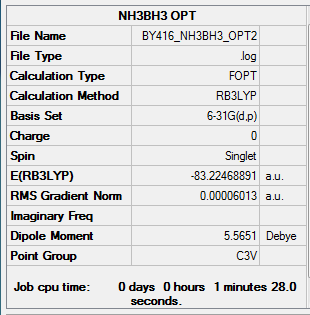
NH3BH3
Method:B3LYP
Basis set:6-21G (d,p)
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000513 0.001800 YES RMS Displacement 0.000296 0.001200 YES
Media: File:BY416 NH3BH3 OPT.LOG
Ng611 (talk) 19:18, 4 June 2018 (BST) ... And here.
Low frequencies --- -13.6017 -0.0013 -0.0007 -0.0003 19.4531 43.3457 Low frequencies --- 266.2693 632.1302 638.2535
NH3BH3 molecule |
Energy Calculations:
E(BH3)= -26.61532364 a.u
E(NH3)= -56.55776873 a.u
E(NH3BH3)= -83.22468893 a.u
Association energy, deltaJ : E(NH3BH3) - [E(NH3)+E(BH3)] = -0.05159656 a.u
-0.05159656 x 2625.5 = -135.4667683 kJ/mol
The energy calculation shows that the B-N bond is weak. The bond enthalpy is +135 kJ/mol. This is lower than other organic bonds.[2]
Ng611 (talk) 19:19, 4 June 2018 (BST) The final value should be reported to the nearest kj/mol
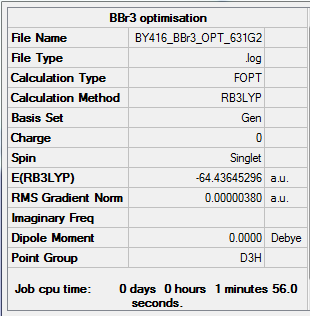
BBr3
Method:B3LYP
Basis: 6-31G (d,p) for B, LanL2DZ (pseudo-potential) for Br
Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.000118 0.001800 YES RMS Displacement 0.000069 0.001200 YES
Low frequencies --- -3.1706 -0.0002 -0.0001 0.0000 1.6540 3.3467 Low frequencies --- 155.8924 155.9627 267.7046
BBr3 molecule |
Project : Aromaticity
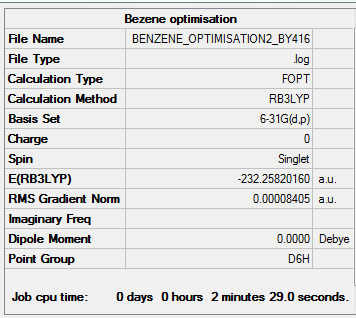
Benzene
Method:B3LYP
Basis set:6-21G (d,p)
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000082 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000305 0.001200 YES
Low frequencies --- -11.6728 -0.0010 -0.0008 0.0003 6.6686 15.6846 Low frequencies --- 414.0392 414.6031 621.0860
Benzene |
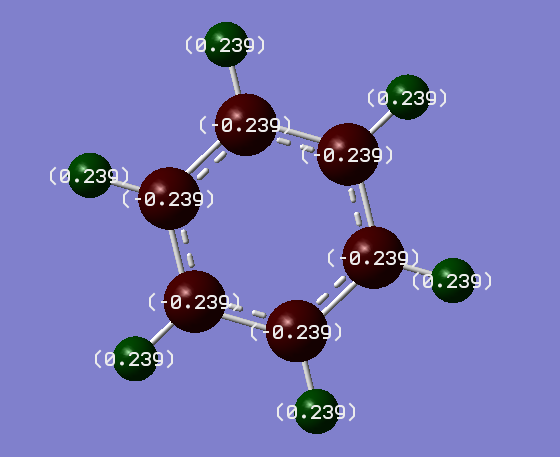
Charge distribution:
Charges:
Carbon = -0.239
Hydrogen = 0.239
Discussion:
In benzene, every carbon atom has the same electronegativity, therefore has the same charge. The same applies to the hydrogen atoms. The hydrogen atoms have the same magnitude of charge as carbon, but the opposite sign.
Borazine
Method:B3LYP
Basis set:6-21G (d,p)
[[File:Borazine opt2 by416.PNG]
Item Value Threshold Converged? Maximum Force 0.000073 0.000450 YES RMS Force 0.000026 0.000300 YES Maximum Displacement 0.000298 0.001800 YES RMS Displacement 0.000106 0.001200 YES
Low frequencies --- -15.3480 -15.3480 -12.7393 -0.0158 -0.0107 -0.0107 Low frequencies --- 288.9049 288.9049 403.7235
Borazine |
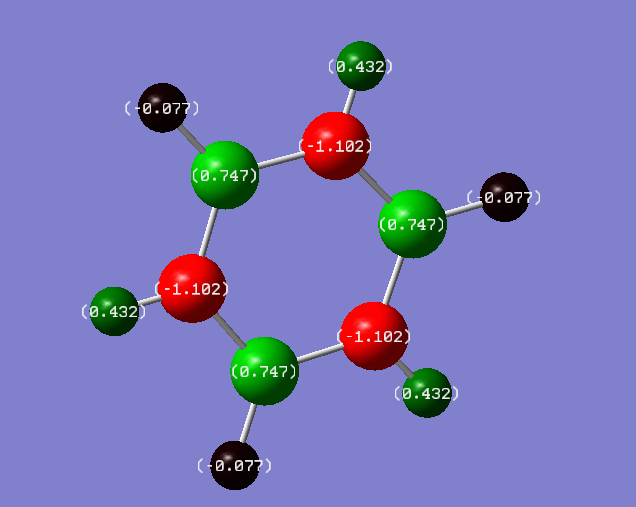
Charge distribution:
Charges:
Nitrogen= -1.102
Hydrogen atoms bonded to Nitrogen= 0.432
Boron= 0.747
Hydrogen atoms bonded to Boron= -0.077
Discussion:
Nitrogen is much more electronegative than boron and hydrogen. Therefore, it pulls electron density from orbitals of B and H, towards itself. As a result the hydrogen atoms bonded to nitrogen have a positive charge because electron density has been pulled away. On the other hand, boron is less electronegative than nitrogen so does not pull as much electron density towards itself. Therefore, it has a less negative charge and its electron density is dispersed on the hydrogen. Hence the hydrogen atoms bonded to boron are more negative than the hydrogen atoms bonded to nitrogen.
Charge Comparison
Borazine has N - H bonds which are more polar than benzene and B - H bonds which are less polar than benzene. This is because nitrogen is more electronegative than carbon. Hence creating bonds with a greater charge difference/ more polar. Boron is less electronegative than carbon therefore there is lower charge difference between B-H than C-H.
Ng611 (talk) 19:21, 4 June 2018 (BST) Good discussion of the effects of electronegativity on the overall charge distribution. What do the partial charges sum to, and is there any difference in partial charge for atoms related by symmetry?
MO Comparisons
1.
These MO diagrams represent p orbitals. 3 p orbitals are in the same phase on either side (the grouping of electron density). The phases are distinguished by colour. In between the areas of electron density, there are nodes where the likelihood of finding an electron is 0. For benzene, the electron density is distributed evenly among the p orbtials in the same phase. This is because all the carbons in benzene are of the same electronegativity. However, for borazine, the electron distribution is gravitated towards the nitrogen atoms (blue atoms). This is because nitrogen is much more electronegative than boron, as discussed before when considering charge density.
Ng611 (talk) 19:24, 4 June 2018 (BST) Which p-orbtials are responsible for the overall MO here? A comment about the symmetry of the orbitals and the symmetry of the molecule here would also be useful.
2.
This example is also looking at p orbitals. As mentioned in the other examples, the distribution is more equal in benzene than borazine. In borazine, the orbitals are skewed because of the different electronegativities. The distribution is even in benzene because the electronegativies are the same.
3.
This example also looks at P orbitals, here all the p orbitals are in the same phase. Only the above place is showing in the pictures, there is also an orbital underneath. The image was taken like this to see the distribution of one orbital. In this case the electron density is distributed equally among the benzene. This is because of the equal electronegativty of the carbons. In borazine, however, the spread of electron density is less equal. The nitrogen atoms have more electron density surrounding them, because of their higher electronegativity.
Aromaticity
For a molecule to be aromatic it needs to obey certain rules. These rules include: being cyclic, planar. all the atoms being conjugated and obeying the 4n+2 rule. The 4n+2 rule, also known as huckle's rule, states that for a molecule to be aromatic it must have the right number of pi electrons. This right number is 4n+2, which is the mathematical shorthand for the series: 2,6,10,14,18... where n must be an integer. Therefore, for the molecule to be aromatic it must have pi electrons that equal to a number in that series. For example, even though clyclooctatetraene is cyclic, conjugated and planar it is not aromatic as it has 8 pi electrons.
The basic conceptions of aromaticity are a simplified version of the MOs. For example, the idea of conjugation is rigid as it assigns electrons to certain bonds. However, as shown in the MO diagrams, the electrons can be found anywhere in the orbital. Furthermore, the idea of aromaticity originated from benzene. The rules assigned, also based from benzene/aromatic compounds, do not apply in some cases. For example benzene is not planar in certain conditions. The idea of aromaticity can also be applied to compounds which are not the conventional aromatic compounds. Some examples include polyhedral boranes, metallobenzenes and fullerenes.
Ng611 (talk) 19:27, 4 June 2018 (BST) This is a promising paragraph. You should go into far more detail though regarding these concepts of aromaticity. For example, what new concepts of aromaticity have arising to explain aromaticity in the compounds you mention. What experiments can be performed to see whether aromaticity is actually occuring?
The Pz orbitals are not conjugated in the pi system therefore they cannot be considered when looking at aromaticity. The orbitals are not conjugated because their orientation/angle is not at the correction orientation to allow the pi orbitals to create a conjugated system. Therefore, it is not a good description for aromaticity.
Ng611 (talk) 19:27, 4 June 2018 (BST) A good report overall. You let yourself down slightly in the final section (the discussion on aromaticity) and in uploading the wrong data for two of your calculations. Otherwise, this was a good piece of work overall. Well done.