Rep:Mod:bwvb5394

Module 2: Bonding (ab initio and density functional molecular orbital (DFT))

Inorganic Experiments

Introduction

Ab initio and DFT are quantum mechanical methods that enable the interpretation of the properties, structure and bonding of molecules. GaussView is used here to carry out these calculations on simple inorganic molecules followed by increasingly more complex exapmles which require more iterative steps and therefore have a much longer processing time. Consequently in each calculation a compromise has to be reached between the time that the calculation takes and the accuracy of the output data. The accuracy of a calculation depends on the calculation method, basis set and the number of cycles used. In the case of the large molecules in the mini project, a smaller number of cycles was used in order to shorten the timescale of the computation.

BH3

Optimisation

1. B-Cl bond distance=1.86592A.
2. The Cl-B-Cl bond angle is 120 degrees.
3. The output file is a .log.
4. The calculation type is an FOPT.
5. The calculation method is RB3LYP.
6. The basis set is LANL2MB.
7. The final energy is -69.4 a.u.
8. The dipole moment is 0 Debye.
9. The point group is D3h.
10. The calculation took 12s.

Vibrational Analysis

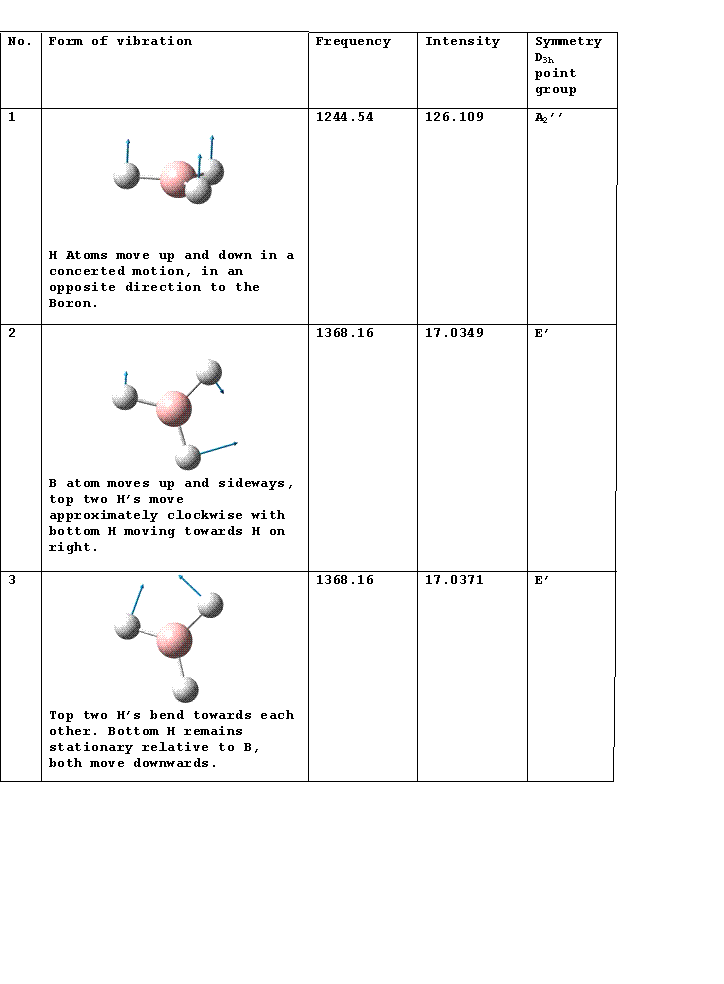
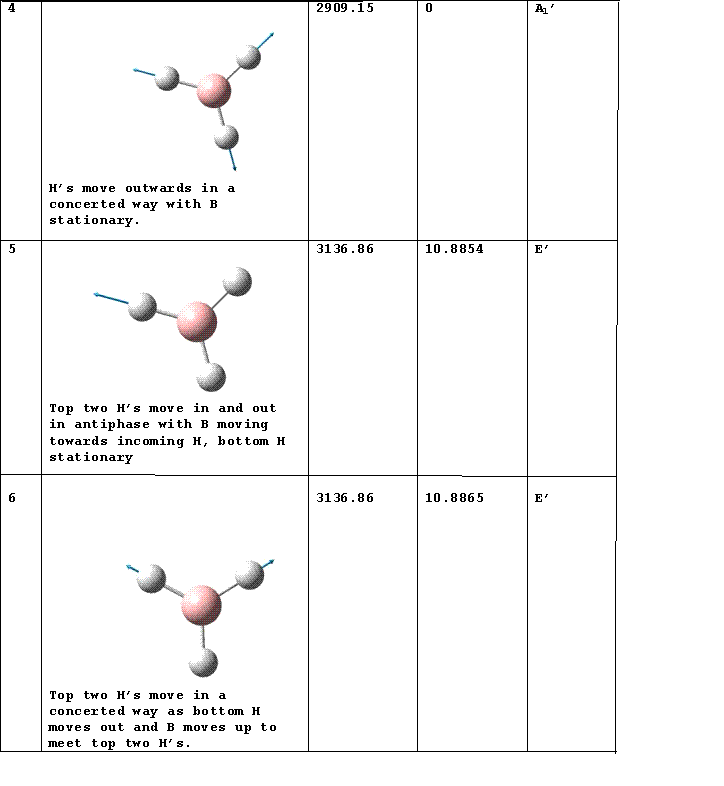
IR Spectrum

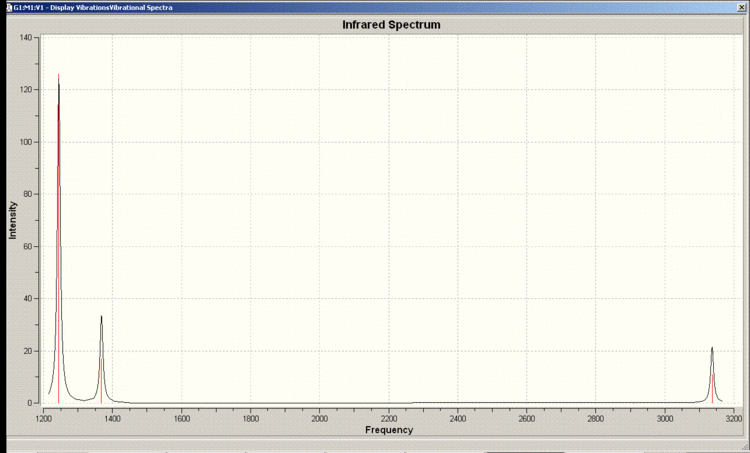
Vibrations 2 and 3 as well as 5 and 6 occur at the same frequency so appear as one peak in the spectrum. There is a selection rule for IR spectroscopy requiring a change in the dipole moment. Vibration 4 does not incur a change in the dipole moment so does not appear in the spectrum.

MO Diagram

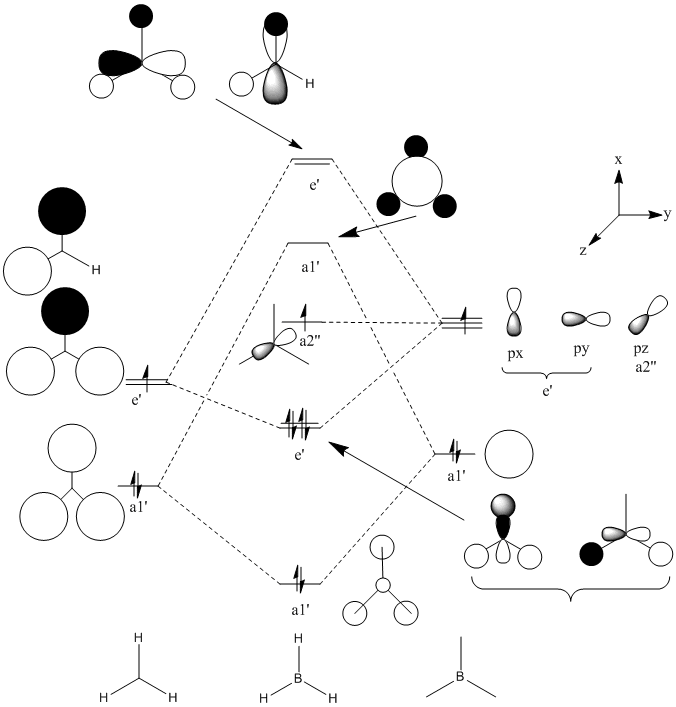
MO's

a1' Bonding orbital

a1' Bonding orbital

e' Bonding orbital

e' Bonding orbital

e' Bonding orbital

e' Bonding orbital

a2"Non-bonding orbital (HOMO)

a2"Non-bonding orbital (HOMO)

a1' Anti-bonding orbital (LUMO)

a1' Anti-bonding orbital (LUMO)

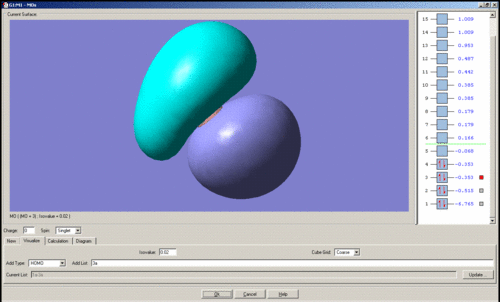
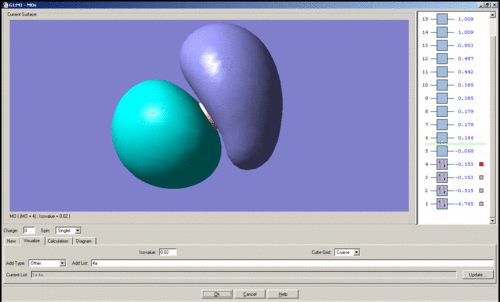
In general it is quite easy to distinguish one quantitative molecular orbital (MO) from another by the position and number of nodes present, for instance the qualitative e' anti-bonding orbitals may be assigned to their respective quantitative orbitals by the position of the node that lies perpendicular to one of the B-H bonds. The qualitative a1' bonding orbital is surprising because the electron density should be concentrated on the hydrogen atoms as their atomic orbitals lie closer to the MO than boron's, however the simulation seems to show that the opposite is true. For the topmost e' bonding orbital, as shown above, it was expected that the electron density would reside mostly along one side of the molecule, around the H-B-H region in which there is orbital overlap. However the electron density according to the quantitative MO, is evenly distributed over the entire molecule. There should also be one node present, but this is not visible. The HOMO is just a non-bonding p-orbital, but the quantitative MO implies that the node of the p-orbital is perpendicular to its expected position and that one of the nodes bares a closer resemblance to a pi-bond due to its diffuse nature than the round lobe of a p-orbital. The LUMO has a node in the plane of the molecule rather than nodes through the plane which would be guessed from the quantitative MO's, giving the MO the appearance of a very large p-orbital on boron.

The images of the qualitative MO's shows that quantitative MO theory generally cannot be used to accurately predict the form of the final MO and therefore the distribution of electron density throughout a molecule. However it is useful for predicting which atomic orbitals combine, how many molecular orbitals there are, their relative energies and occupation.

Small Molecule, H2S

Atom	x-coordinate	y-coordinate	z-coordinate
S	0.000000	0.000000	0.104421
H	0.000000	1.008809	-0.835365
H	0.000000	-1.008809	-0.835365

1. S-H bond distance= 1.37873A.
2. H-S-H bond angle= 94.05736 degrees.
3. The calculation method is RB3LYP
4. The basis set is 6-31G
5. The final energy is -399.35499679 a.u.
6. Dipole moment= 1.8022 Debye.
7. The point group is C2v.
8. The calculation took 22.0s.

Transition Metal Complex: [Bis(trimethylphosphine)tetracarbonyl molybdenum]

Important Geometrical Parameters

(Optimised geometries: Trans DOI:10042/to-? 10042/to-? , Cis DOI:10042/to-1109 10042/to-1109 )

Molecule	Bonds	Bond angle/Degrees	Bond distance/Angstroms
Trans isomer	C-P-C	101.4-101.6	C-P 1.890
	P-Mo-C	88.9-91.1	C-Mo 2.029
	P-Mo-P	180.0	P-Mo 2.573
	C-Mo-C	89.99-90.01	C-Mo 2.029
Cis isomer	C-P-C	100.6-101.4 (101.9)	C-P 1.890-1.895 (1.84)
	P-Mo-C	88.2-90.6 (116)	C-Mo 2.033
	P-Mo-P	92.94 (94.78)	P-Mo 2.648 (2.529)
	Cis carbonyls, trans to PMe3, C-Mo-C	89.07	C-Mo 1.982 (1.982)
	Trans carbonyls, cis to both PMe3's, C-Mo-C	178.3	C-Mo 2.033 (2.016)

Note: literature values are given in brackets for a similar complex, which differes only by having PMe2Ph ligands rather than PMe3 ligands.

The P-Mo-P bond angle is relativrly for the cis isomer large compared to the typical trans anlges which are around 88-91 degrees. This is due to the the steric hindrance of the bulky PMe3 groups, the literature value is even larger due to the more bulky phenyl substituent. The P-Mo-C angle is large for the literature compound presumably beacsue the presence of the bulky phenyl groups compresses the carbonyl ligands together. The larger range C-P bond distance for the cis isomer is due to the two methyl groups that are nearest to each other in the cis PMe3 ligands.. Only this C-P bond in each PMe3 ligand is substantially longer than the others and it appears to minimise the Van der Waals' repulsion. The P-Mo distance is also larger for the cis isomer probably for the same reason.

The trans isomer of the complex investigated could not be found in the literature. A search of the structure was made using Beilstein and a Google search was made using its systematic name.

IR Spectral Information

(Cis:DOI:10042/to-1110 , trans:DOI:? )

Cis/Trans	Vibration No.	Frequency/(1/cm)	Intensity	Functional Group/Bond
Cis	28(assymetric stretch)	311.16	14.04	Mo-P
	29(symetric stretch)	312.76	11.54	Mo-P
	32(assymetric stretch)	421.25	43.34	Mo-C (Carbonyls trans to each other)
	33(symmetric stretch)	428.18	0.23	Mo-C (Carbonyls trans to each other)
	34(assymetric stretch)	457.91	1.63	Mo-C (Carbonyls cis to each other)
	35(symmetric stretch)	472.49	0.62	Mo-C (Carbonyls cis to each other)
	78	1849.82	1091.77	C=O (Carbonyls cis to each other)
	79	1851.02	1951.21	C=O (Carbonyls trans to each other)
Trans	28(symetric stretch)	316.81	0	Mo-P
	29(assymetric stretch)	320.04	32.20	Mo-P
	33(assymetric stretch)	428.18	33.68,	Mo-C (Carbonyls trans to each other)
	34(assymmetric stretch)	428.37	43.75	Mo-C (Carbonyls trans to each other)
	78(assymmetric stretch)	1839.20	2002.14	C=O (Carbonyls trans to each other)
	79(assymetric stretch)	1839.46	2006.32	C=O (carbonyls trans to eash other)

The lower frequency of the Mo-P stretches in the cis isomer suggests that the bond is weaker than in the trans isomer. This reflects the longer bond length in the cis isomer. The energy of the cis isomer is 2.030070376 E6 KJ/mol and the energy of the trans isomer is 2.030062874 E6 KJ/mol. The trans isomer is therefore more stable by 7.5KJ/mol. The order of stability could be inverted by introducing substituents to the groups attached to phosphorus which will allow the ligands to have favourable intermolecular interactions when they are close enough, i.e. in the cis position. For instance, amine functionality could be added to alkyl groups attached to phosphorus to encourage hydrogen bonding between the ligands when they are cis to each other.

Ammonia

Symmetry

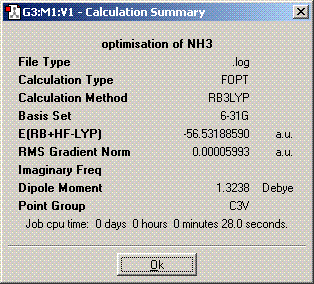
The symmetry is C3v.

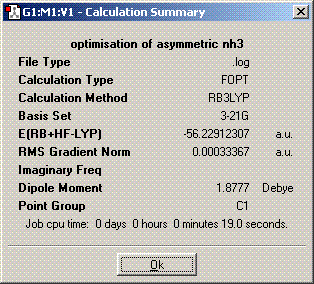
The symmetry is C1.

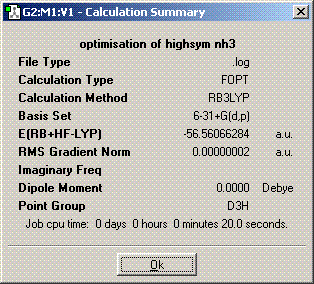
The symmetry is D3h.

The structures of of C1 and C2v symmetries are essentially the same except in the C1 case the bonds are all of different length. The D3h structure is significantly different in that it is planar so has a σh plane of symmetry. The C3v molecule took longer to compute than the other symmetries. It took longer then dor D3h probably because there is an extra plane (3D rather than 2D) to consider when adjusting the bond angles and distances and it probably took longer than C1 because it is of higher symmetry. A molecule can lose its symmetry during an optimisation as the bond distances and angles are altered, this could result in a high symmetry molecule having a different point group after it has finished being optimised. The lowest energy geometry is D3h. The energy of the C1 molecule is 870.3KJ/mol higher than the D3h molecule and the C3v molecule is 75.5KJ/mol higher. The energy difference here is significant because of the long bonds in the c1 molecule whch are far from their equilibrium bond length so their is a positive potential energy gain for each bond.

Calculation Method

The higher level MP2/6-311+G(d,p) calculations took approximately 20-30% longer to complete than the B3LYP/6-31G calculations for the same molecules, 31 seconds for D3h and 33 seconds for C3v. The barrier height to inversion for NH3 is 20.46KJ/mol. The energy difference is much smaller this time, it is over 55KJ/mol less. The result obtained this time around is in very good agreement with the experimental value of 24.3KJ/mol.

Vibrational Analysis

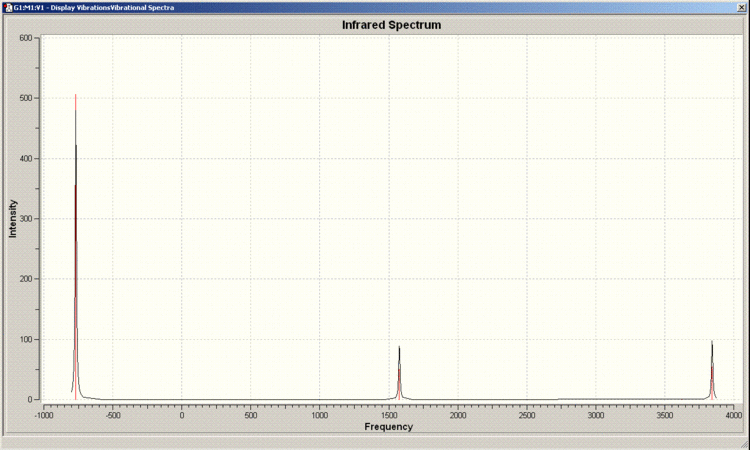
IR Spectrum of D3h Molecule

IR Spectrum of C3v Molecule

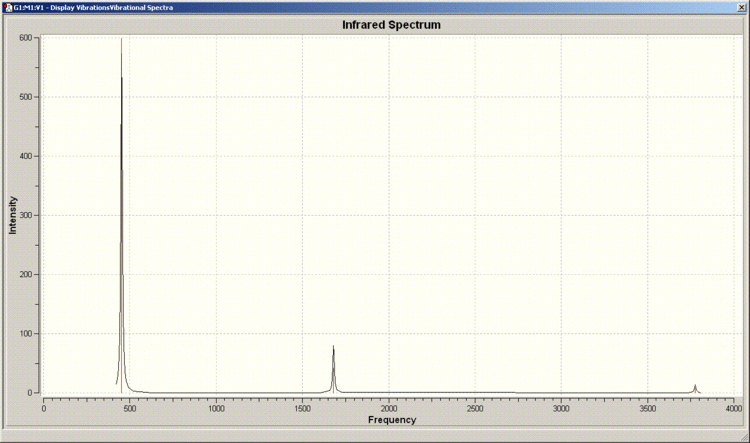
There are 6 positive frequencies for the C3v molecule and 5 for the D3h molecule.

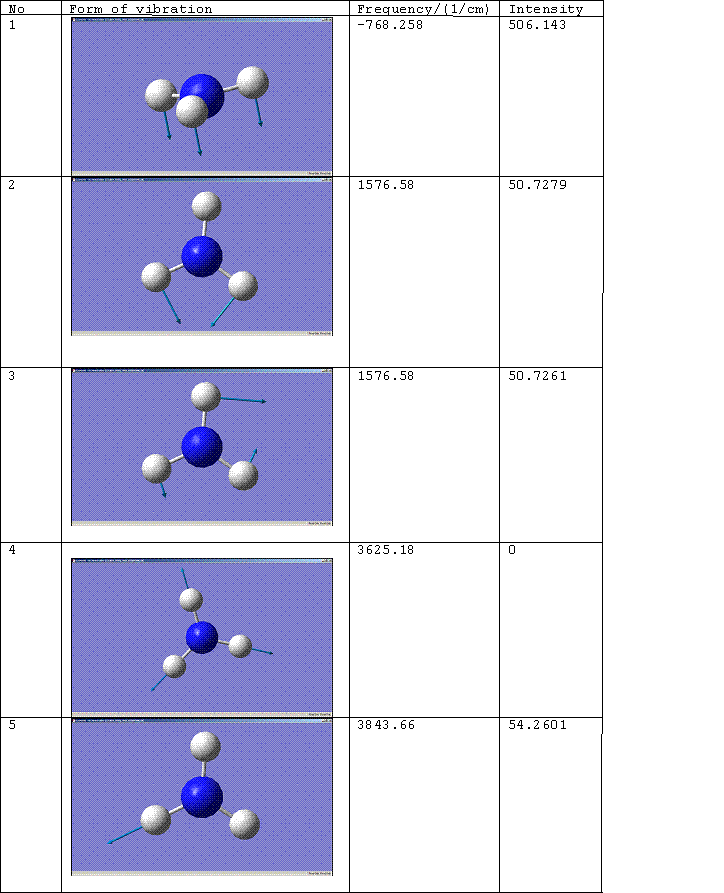
D3h Molecule

C3v Molecule

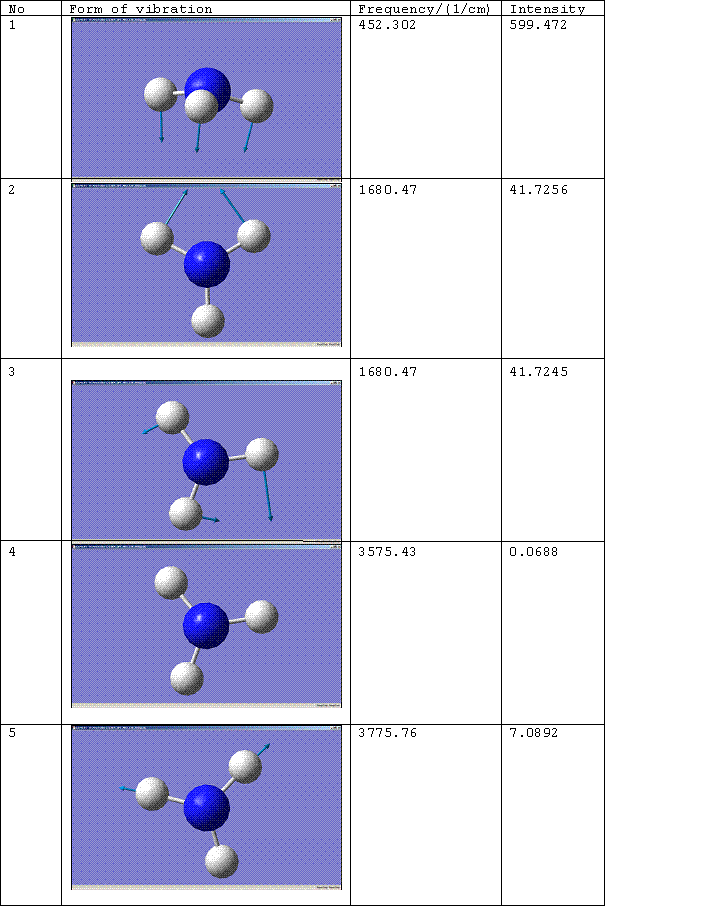
The number of the vibration corresponds to the same mode of vibration for both molecules, except that vibration 5 for the D3h molecule should be paired with vibration 6 for the C3v molecule. The change of the frequency for vibration 1 from a negative value to a positive one shows that the force constant of the bond has increased implying that the C3v molecule is the more thermodynamically stable conformation, i.e. the product rather than the transition state. For more on this see, Z. Zhou, W. Zhao, L. Chen and Q. Yu. Vibration 1 therefore follows the inversion reaction path.

Literature values for the vibrational frequencies of ammonia are 7548.0, 1689.9(1680.47), 3591.6(3775.76), 1030 and 3503 cm^-1. . The matching calculated frequencies are given in brackets.

Mini Project

Introduction

[FeFe] Hydrogenase is an enzyme with the ability to reduce protons toe hydrogen. The enzyme accomplishes this by binding to protons via initially one of the iron atoms before forming a hydride complex involving both iron atoms. It is the aim of synthetic research chemists to design a complex which will perform the same function to act as "cheap electrocatalysts for hydrogen evolution" as well "more economical electrode materials as alternatives to platnum in fuel cells" , but doing this without the surrounding protein structure presents a few challenges, see C. M. Thomas, T. Liu, M. B. Hall and M. Y. Darensbourg for more information.

1. The iron must be sufficiently basic to bind to a proton.
2. The conformation of each iron may have to be twisted relative to the other iron in terms of the position of each ligand set as is the case in the enzyme.

I will investigate the effects of using different ligands on the basicity of the iron ions. The focus will be on the pi-acceptor/donater ability of the ligands and the effect this has on the electron density at the diiron centre.

The model considered by G. Hogarth and I. Richards is [Fe2(CO)3(μ-pdt){μ,η2-Ph2PCH2CH2P(Ph) CH2CH2PPh2}] (pdt = SCH2CH2CH2S). However to simplify the DFT calculations, the phenyl groups of the tridentate ligand have been replaced with methyl groups. The CO ligands have then been substituted for others of varying pi-acceptor ability, in order these are: H2O < NH3 < CO. It is expected that as the pi-acceptor ability decreases, the electron density at the diiron centre will increase, meaning that it is more likely to pick up a proton and thus the complex will be a better model of the enzyme.

The compound [Fe2(CO)6(μ-pdt)](pdt = SCH2CH2CH2S)will also be looked at since the iron ions here are reportedly "not basic enough to bind a proton" it could therefore be useful as a basis for comparison of the basicity of the diiron centre. The tridentate ligand was introduced to break the symmetry of the complex so that one of the iron ions would be rendered more basic than the other and to attempt to twist the conformation of the complex so that it more accurately resembled the enzyme.

Geometry Optimisations

All of the optimisations here were carried out using RB3LYP/6-31G (which is one of the simpler calculations and lower level basis sets) beacause the molecules dealt with here are quite complex so a calculation level higher than this would be time consuming. For the complex without the tridentate bridge the maximum number of cycles was set to 25, but for all the other complexes this was set to 2 initially to obtain an estimate of the time required for a reasonably accurate computation. These trial runs took around two hours to complete so these optimised geometries were then submitted overnight to run through 10 cycles.

[Fe2(CO)6(μ-pdt)](pdt = SCH2CH2CH2S) (DOI:10042/to-1111 )

tetcarb

[Fe2(CO)3(μ-pdt){μ,η2-Me2PCH2CH2P(Me)CH2CH2Me2}] (pdt = SCH2CH2CH2S) (DOI:10042/to-1112 )

methyls

An interesting point here is that the Fe-Fe bond distance is only 2.46579 Angstroms compared to that seen by Hogarth and Richards of 2.5279 Angstroms, in the analogous complex with phenyl groups in place of the methyls. This is perhaps indicative of the lower steric strain due to the less bulky methyl groups. The assymetry introduced by the phosphine ligand is clear and there is a slight increase in the degree of staggering of the eclipsing CO logands from 11.95 and 12.87 degrees in [Fe2(CO)6(μ-pdt)], to 16.78 degrees in [Fe2(CO)3(μ-pdt){μ,η2-Me2PCH2CH2P(Me)CH2CH2Me2}], providing a conformation which is very slightly closer to that found in the enzyme.

[Fe2(NH3)6(μ-pdt)](pdt = SCH2CH2CH2S) (DOI:10042/to-1113 )

ammonia

[Fe2(H2O)6(μ-pdt)](pdt = SCH2CH2CH2S) (DOI:10042/to-1114 )

water