Rep:Mod:bwph3895
Module 3: Experiment 3-The Transition State
Introduction
The transition states of molecules can be modelled to provide insight into kinetically controlled reactions, which depend upon the transition state energy barrier along a reaction pathway. Here, the GaussView program has been utilised to carry out this modelling. Reacting molecules have been optimised to their transition states using the TS QST2 and TS (Berny) methods to provide insight into why certain transition state conformations are favoured over others. Also, the pathway proceeding from the transition state to the product occupying the first local minimum along the potential energy surface has been analysed using the an IRC (internal reaction coordinate) calculation. Finally, a quantitative molecular orbital interpretation of the transition state is made to help rationalise the preferred transition state for a reaction.
The Cope Rearrangement Tutorial
Optimizing the Reactants and Products
Conformation A
cisbute |
Energy=-231.68907a.u. Point group: C2h/C1. Gauche conformations are likely to be of higher energy than anti conformations due to increased steric interaction between the terminals of the diene, which are brought closer together in the gauche conformation.
Conformation B
cisbute |
E=-231.68772a.u. Point group: C2/C1. The most stable conformation will be one where the steric clash of the terminals ends is minimised.
Conformation C
cisbute |
E=-231.69254. Point group: Ci/C1. The conformation above is the lowest in energy so far which make sense as the terminals are far apart from each other.
Conformation D
cisbute |
E=-231.69167a.u. Point group: C1/C2.
Conformation E
cisbute |
E=-231.69266a.u. Point group: C1.
The conformer above is the most stable so far, disproving my hypothesis that anti conformations would be more likely to have greater stablilities for steric reasons. This is unexpected because it has a relatively crowded appearance compared to conformation A for instance and consequently one would expect the energy to be quite high for steric reasons. However, there must be other factors affecting the stabilities here. In the gauche structure above, each alkene has a hydrogen on an adjacent carbon peri-planar with respect to the p-orbitals, enabling possible overlap of a filled p-orbital with the σ* C-H orbital of the vicinal carbon, in other words hyperconjugation. It is clear that the most unstable gauche and anti conformations lack this planar p-orbital/hydrogen arrangement.
The second anti structure shown above corresponds to "anti 2" in the table. The energy is the same as tabulated. After a B3LYP/6-31G optimisation, the following geometry was obtained.
Conformation C
cisbute |
E=-234.55970a.u. and the symmetry is C1/Ci. The dihedral angles between the central CH2s' hygrogens have increased from 62.83 degrees to 64.13 degrees relieving the Van der Waals' repulsive interaction. The overall energy has decreased substantially, by nearly 3a.u., under this higher level calculation. The point group is the same as before. In general, the stabilisation gained through hyperconjugation, evident in conformations C,D and E, far outweighs the destabilistion caused by Van der Waals's repulsion.
Vibrational Frequency
Sum of electronic and zero-point Energies=-234.416245 Hartree/Particle
Sum of electronic and thermal Energies=-234.408954 Hartree/Particle
Sum of electronic and thermal Enthalpies=-234.408010 Hartree/Particle
Sum of electronic and thermal Free Energies=-234.447848 Hartree/Particle
Optimizing the "Chair" and "Boat" Transition Structures
In order to obtain an accurate result for the transition strucure calculations involving two allyl fragments, the allyl fragment was first optimised using the HF/3-21G method, giving the geometry shown below. The C=C bond distances are 1.39 Angstroms, which is typical and a C-C-C angle of 124 degrees, probably slightly larger than the expected angle of 120 degrees for an sp2 hybridised system so that the Van der Waals' interaction between the almost parallel terminal hydrogens is minimised.
cisbute |
Chair Transition Structure
Staroverov and Davidson[1] suggest that the Cope rearrangement occurs via either a stepwise radical process or a concerted mechanism whereby one bond is made between the terminal ends and one is broken. Furthermore, whichever route is correct, a chair-shaped intermediate with delocalised π-electrons is always formed as illustrated below by the diagram borrowed from their research paper.
The following structure was used as the input file, with the terminal C-C distances having been set to 2.2 Angstroms, a peculiar result emerged however.
cisbute |
Following optimisation to a TS (Berny), the structure below was obtained. Strangely, the optimisation has carried on past the transition state and formed the diene product, with a gauche conformation of energy -231.68417a.u., which seems to be a relatively very unstable conformation, in fact it is the least stable encountered so far due to the eclipsing hydrogens of the alkene C-H and adjacent alkane C-H. The reason for this may be that the distances between the sets of terminals were not exactly equal in the input file leading to the assumption by GaussView that the structure was not in fact a transition state.
cisbute |
After optimisation using the redundant coordinate editor, the structure below was obtained, which is not in fact the chair transition state. The same problem appears to have occurred as before in that the product has been obtained instead of the transition state, except this time the structure has been optimised to the more stable (as previously calculated) conformation B. However, the energy this time is higher (E=-231.49045a.u.) compare to when conformation B was optimised earlier on (E=-231.68772a.u.), showing that although the same calculation method of HF/3-21G has been used, the final energies are different. This is either because a different starting point was used in terms of the geometry as this time around a starting geometry further from the final geometry was used (two separate molecules) or it is beacause this calculation was supposed to optimise to a transition state rather than just optimise one molecule. The latter reason is the most probable explanation as the same level of theory should give the same result every time.
cisbute |
A second optimisation using the redundant coordinate editor was performed, this time the fragments were placed almost directly on top of each other, less staggered than before. This gave the correct, chair transition geometry as shown below.
cisbute |
The terminal distances were initially ~2.2 Angstroms prior to the calculation and during the coordinate freeze of the terminal carbons, but these distances have been reduced to 1.79 Angstroms. It is clear that the allyl fragments are now bent towards each other and the hydrogens are approaching their respective 'axial' and 'equatorial' positions that would be seen in cyclohexane for example. Also the H-C-H angles at the terminals have been reduced from 117 degrees to 111 degrees, which reflects the change in hybridisation from sp2 to an sp3 like centre.
The success of the calculation this time demonstrates the importance of the geometry of the fragments relative to each other in the input file because that is all that has been changed here. When the allyl fragments are on top of each other, as is the case here, it enables better overlap of the p-orbitals on the terminal carbons to occur as they approach each other head-on.
Boat Transition Structure
After optimising the allyl fragments to a QST2 transition state, the structure below resulted. The calculation failed to arrive at the boat conformation due to a reluctance of one of the allyl fragments to make a 180 degree rotation.
cisbute |
Changes were then made to the allyl fragments to bring then more closely to their transition state conformation. The central dihedral angle was set to 0 degrees and the central C-C bond angle was decreased to 100 degrees. The structure below is the result of an optimisation of these manipulated fragments using QST2.

Energy=-231.60280a.u.. The imaginary frequency for the coming together of the fragments is -840.135cm^-1. The terminal transition state 'bond lengths' are 2.14 Angstroms. This transition structure most closely resembles conformation E. It can be seen that the energy of the chair is lower than that of the boat by 0.08137a.u.
Internal Reaction Coordinate Method - Successful Attempt
An IRC calculation for the chair transition state yielded the following structure. The number of steps used was 50. The formation of a bond between one set of terminals is clear owing unequal distances between the sets of terminals and the receding hydrogens.
cisbute |
Graphs Showing Energy Change and Rate of Energy Change

The top graph almost passes through a point of inflection, which is represented in the bottom graph by the minimum around 2.75 on the x-axis (reaction coordinate).
After optimising this structure using a B3LYP/6-31G calculation the structure below was obtained. The molecule has been optimised to conformation D, one of the lower energy gauche conformation due to the high degree of hyperconjugation consequent of the peri-planar C-H and p-orbital discussed previously.
cisbute |
After increasing the number of points in the IRC to 100 the structure below resulted. The same result has been arrived at as above, i.e. conformation D.
cisbute |
Graphs Showing Energy Change and Rate of Energy Change

The convergence to the minimum energy is much better this time with a exponential decay in the energy.
After always calculating force constants the structure below was reached. This is the the least good method out of the three since the molecule is not yet fully optimised, the alkene p-orbital and vinylic alkane C-H are not yet peri-planar and the two terminals are more sterically hindered due to their closer proximity compared to the other structures.
cisbute |
Internal Reaction Coordinate Method - Failed Attempt
All of the work below was done using the wrong structure for the chair transition structure (see below). The Berny optimised chair transition structure was submitted for an IRC calculation. The IRCMax option was included initially, but this led to the following error: "Error termination in NtrErr". The number of cycles was set to 25 in an attempt to solve the problem, however further errors occurred so the IRCMax option was finally neglected. The strucutre below is of the the final step in the calculation, i.e. the lowest energy conformation.
cisbute |
E=-230.16925a.u.
Graphs Showing Energy Change and Rate of Energy Change
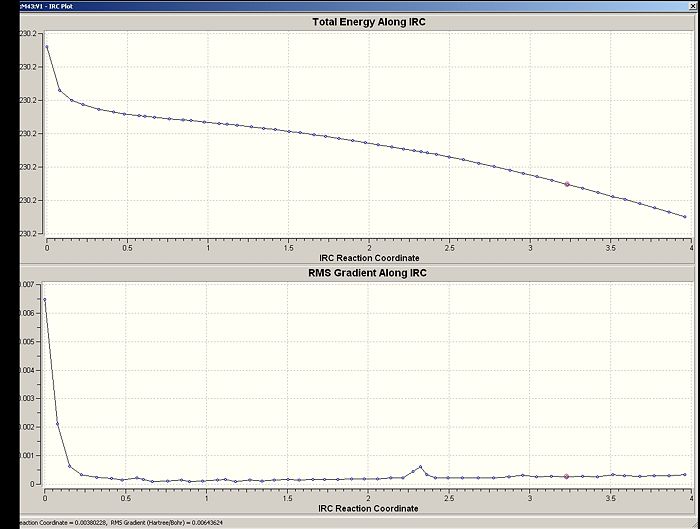
After optimising the structure from the final step using a HF/3-21G method, the following conformation was obtained.
cisbute |
Energy=-232.89414a.u. Calculation time=52s. After increasing the number of points used in the calculation to 100, the structure below was obtained.
cisbute |
Energy=-230.17317a.u. Calculation time=17min 4s. Interestingly a new gauche conformation has been adopted after an optimisation and after increasing the number of calculation popints to 100. The same pattern is shown above where the teo different strategies of increasing the number of points used or running an optimisation to minimise the energy lead to the same result.
Graphs Showing Energy Change and Rate of Energy Change
The erratic behaviour of the potential energy change along the reaction coordinate provides a good indication that something is wrong.
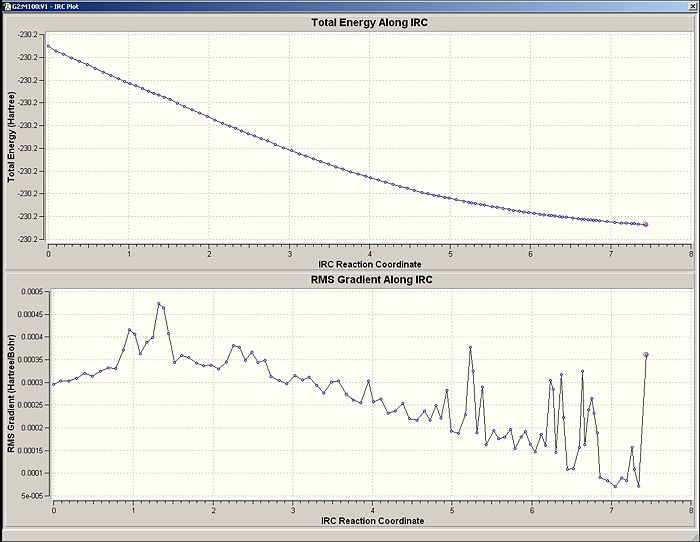
After calculating force constants at every point the structure below was obtained.
cisbute |
Energy=-230.16985a.u. Calculation time=12min 34s. Once again, calculating force constants has led to a structure less well optimised compared to the other two methods, with a poorer p-orbital/C-H σ* overlap.
The best way to optimise a molecule after running the initial IRC calculation is to run an optimisation as this takes the least time (if the level of theory is increased to B3LYP-6-31G then the time taken is comparable to the other methods, but it is still quicker than using 100 calculation points) and gives the same result as increasing the number of calculation points. The worst method to use is to calculate all force constants because this takes a long time and the end result is not as good as with the other methods.
Activation Energies
Chair
After a B3LYP/6-31G optimisation the following geometry was obtained.
cisbute |
Energy=-234.36267a.u. Eact=33.1Kcal/mol.
Boat
cisbute |
Energy=-234.35498a.u. Eact=38.1Kcal/mol. The activation energies given in the literature are 33.3±0.5 Kcal/mol for the chair and 44.4±2.0 Kcal/mol for the boat[2].
Conformation E
In order to calculate the activation energies for the transition structures, the most stable conformation of the product must be also be optimised using the same caclculation method, i.e. B3LYP/6-31G.
cisbute |
Energy=-234.41574a.u.
Diels Alder Cycloaddition
HOMO and LUMO
Only orbitals of matching syymetry can overlap favourably, giving bonding interactions. Looking at the symmetry of the HOMO and LUMO of the reacting molecules in the Diels Alder reaction provides a way of qualitatively understanding the reaction mechanism. The symmetry of the HOMO's and LUMO's in this section are assessed relative to the plane of symmetry shown below.

Cis-butadiene
The HOMO of cis-butadiene is shown below. It is anti-symmetric with respect to the plane of symmetry.
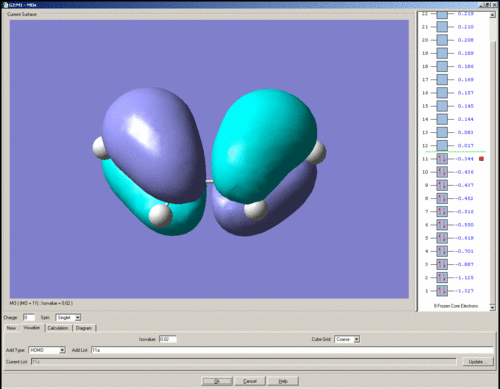
The LUMO of cis-butadiene is shown below. It is symmetric with respect to the plane of symmetry.
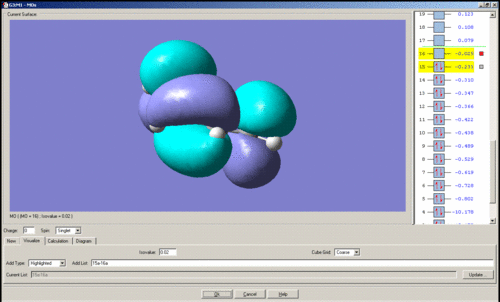
Ethene
The HOMO of ethene is shown below. It is symmetric with respect to the plane of symmetry.
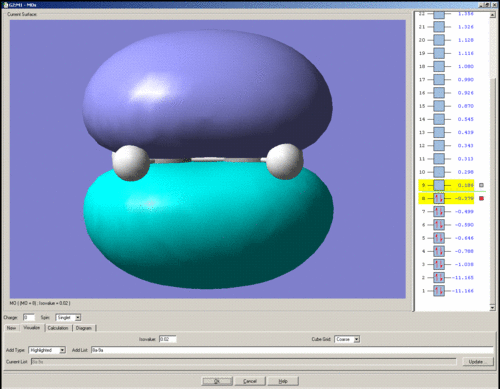
The LUMO of ethene is shown below. It is anti-symmetric with respect to the plane of symmetry.

These frontier molecular orbitals denote that the HOMO of cis-butadiene bonds with the LUMO of ethene and the LUMO of cis-butadiene can interact with the HOMO of ethene.
Transition Structure
The terminals were placed 2 Angstroms apart prior to the calculation and are now approximately 1.55 Angstroms apart (close to the average C-C bond length of 1.54 Angstroms) after an optimisation using the Berny transition state method with the force constants calculated once. The Van der Waals' radius of the carbon atom is 1.70 Angstroms[3], the C-C sp2 bond length is 1.34 Angstroms and the C-C sp3 bond length is 1.54 Angstroms. One would therefore expect the bonds that are forming between the terminals in the transition state to be between 1.54 and 1.70 Angstroms so that a compromise is reached between the attractive electron-nuclear force and the repulsive electron-electron interaction. Since the bond length in the transition state is very close to the typical C-C bond length, this indicates that the attractive force far outweighs the repulsive force.
Below is the HOMO for the transition structure shown above. On the whole this MO is symmetric with respect to the plane of symmetry, with the exception of the small amount of electron density at the CH2-CH2 linkage at the front of the diagram.
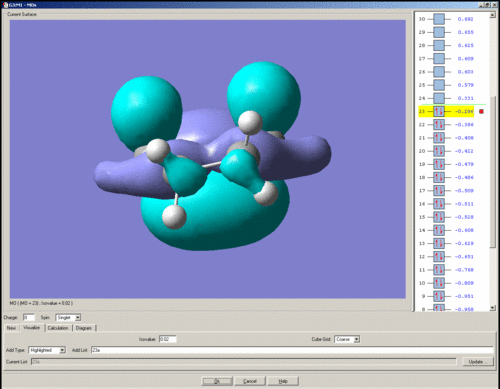
The HOMO is a combination of the HOMO's and LUMO's of ethene and cis-butadiene as described above, the reaction is allowed because orbitals of the same symmetry are combined.
Regioselectivity
Maleic anhydride reacts with cyclohexa-1,3-diene in a Diels-Alder reaction. There are two possible conformations for the product, exo or endo, with the endo product predominating. The reaction is supposedly kinetically controlled, if so then the transition state energy leading to the endo product should be lower. In this section all transition states have been optimised using the TS(Berny) method.
Endo Transition State-Berny
The terminal bond distances were set to 2 Angstroms prior to the optimisation.
cisbute |
The energy is -605.61037a.u. The terminal C-C distance is now 2.23 Angstroms.
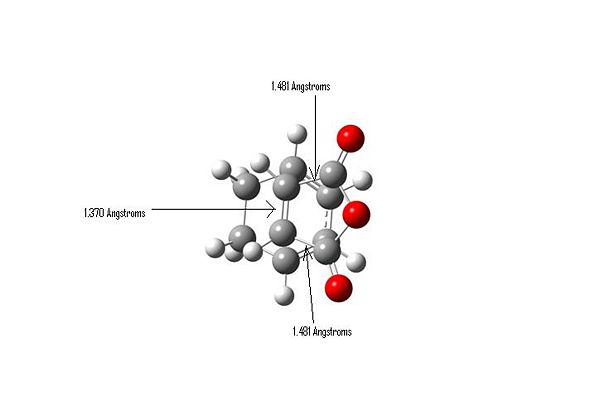
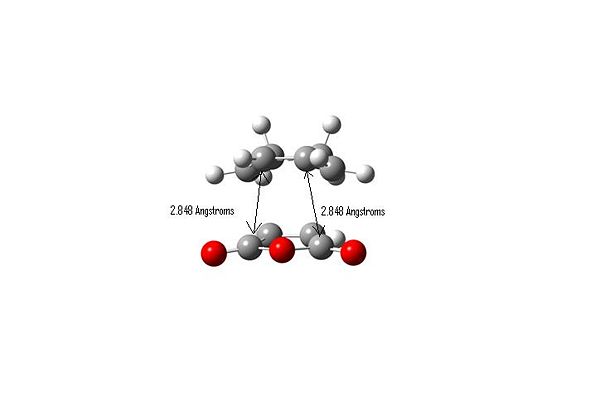
Important Bond Lengths

HOMO
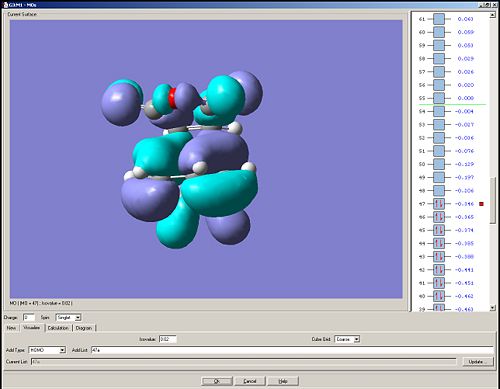
It can be seen that there is a bonding interaction where the C-C sigma bonds are forming. However there is a potential anti-bonding interaction between the central oxygen and the two carbonyls oxygens. This MO is anti-symmetric with respect to the plane of symmetry.
Exo Transition State
cisbute |
Energy=-605.60310a.u. The terminal bond distances have been optimised to 2.26 Angstroms.
Important Bond Lengths

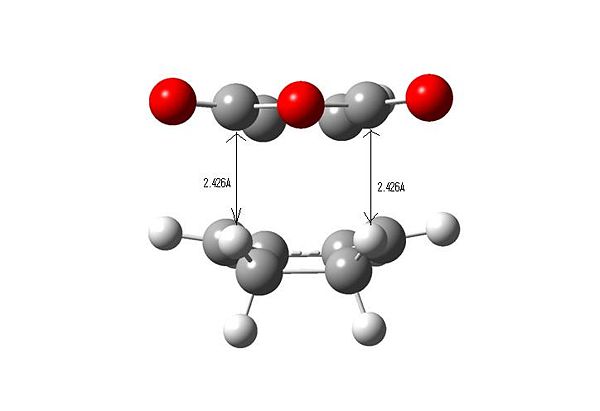
The distances between the atoms on the dienophile that are closest to the C-O-C carbons on maleic anhydride cause the greatest amount of steric hindrance so the distance measurements are to different atoms for the two transition states. It can be seen that the labelled C-H distance (2.426 Angstroms)in the exo transition state is less than the corresponding C-C distance (2.848 Angstroms) in the endo transition state, implying that there is less of an unfavourable steric interaction in the endo transition state, i.e. the exo form is more strained.
HOMO
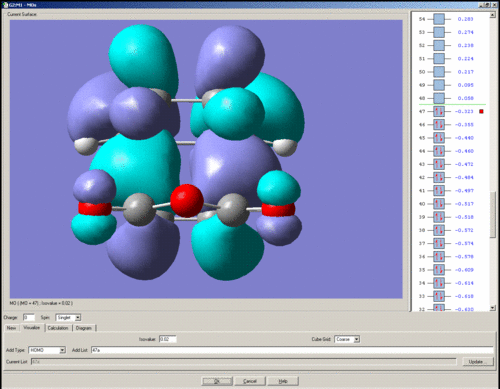
The HOMO is anti-symmetric with respect to the plane of symmetry.
The exo transition structure is approximately 0.01a.u. more stable than the endo form, this is contrary to what was expected and confirms that the calculations have failed to reach a transition structure. The first indication that the calculations did not work was that the terminal bond distances increased from 2 Angstroms, clearly this should not happen since a typical C-C bond distance is 1.39 Angstroms so a bond distance like this or slightly greater should be present in the transition state. This calculation would in all likelihood work if it was repeated with a shorter initial distance between the terminals, e.g. 1.6 Angstroms.
It is odd that although the calculations seem to have failed, there is still a bonding interaction in the HOMO where the σ-bonds would be expected to form.
References
- ↑ V. N. Staroverov and E. R. Davidson, Journal of the American Chemical Society, 2000, 122, 7377-7385. DOI:10.1021/ja001259k
- ↑ Paul G. Wenthold, J. Chem. Soc., Perkin Trans. 2, 1999, 2357 - 2363. DOI:10.1039/a903223a
- ↑ A. Bondi, The Journal of Physical Chemistry, 1964, 68, 441-451. DOI:10.1021/j100785a001
