Rep:Mod:bwalker3
Barnaby Walker
Module 3: Transition States and Reactivity
In module 1 molecular mechanics force fields were used to model reactants and products in order to make judgements about the selectivity observed in certain reactions. Despite being well suited to finding the lowest energy conformation of a molecule, the molecular mechanics method cannot be used to find the transition state of a reaction which involves the breaking of a bond. This is because the force field used in the calculations is unique to a particular combination of atoms, so if a bond is formed or broken during a reaction the force field used for the calculation must change.
However, the quantum mechanics based methods used in Module 2 are much more suited to this application. These will be used to find the transition states and judge the reactivity of the reactants first in the Cope rearrangement of 1,5-hexadiene, and then in the Diels-Alder cycloaddition of various dienes with dienophiles.
The Cope Rearrangement

The cope rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic shift that occurs in a concerted pericyclic fashion through either a boat or chair transition state. It has been reported that the boat TS is higher in energy than the chair TS. It has also been shown that the B3LYP method using the 6-311G(d) basis-set gives activation energies and enthalpies that agree closely with experimentation. As such, Gaussian will be used to predict these values for this Cope rearrangement at such a level of theory, in order to verify that the boat TS is indeed higher in energy.
The first step in doing this is to find the minimum energy conformation of the reactants and products. In this case, the reactant is largely the same as the product, so it is only 1,5-hexadiene that needs to be modelled. Once this has been done, the transition state can be modelled using a variety of methods. By carrying out an optimisation and frequency analysis at the B3LYP/6-311G(d) level of theory for the resultant transition states, information about their energies can be found. The reaction coordinates of the reaction can be found as well by carrying out an IRC calculation.
Optimisation of Reactants and Products
At first a low-level theory, HFT/3-21G, was used to optimise the structure of 1,5-hexadiene. Different starting conformations were drawn to gain different optimised structures, with there being two main classes: those where the two propene groups are anti to each other, and those where they are gauche. In these two classes there are other conformations with smaller differences. A few of these were modelled and the symmetry of them gained using the Symmetrise function in GaussView. These can be seen in the table below.
From the table it can be seen that the lowest energy conformation is the anti geometry with C2 symmetry. In this conformation the two alkene groups are pointing in the same direction, but as far from each other as possible. Looking at the two gauche conformations, the reasons why they are higher in energy than the anti conformations can be found out. For the C2 gauche conformation, although it has the same symmetry as the lower energy C2 anti conformation, the alkene groups are pointing in opposite directions. This leads to greater strain in the gauche conformation, shown by an increase in the bond angle around the central tetrahedral carbon atoms - from 111o in the anti conformation to 112o in the gauche conformation. This would suggest that the overall lowest energy conformation would have the alkene groups pointing in the same direction to minimise this strain.
However, the C1 gauche conformation does indeed have both alkene groups pointing in the same direction. Yet, this is much higher in energy than the other conformations as the alkene groups are very close together. From this an even lower gauche conformation of 1,5-hexadiene can be imagined, with the alkene groups pointing in the same direction as in the C1 conformation, but with them far enough apart not to cause too much strain in the molecule.
This was tested by starting from a gauche conformation with both alkene groups pointing in the same direction, but not too close together. This was then optimised using the HFT/3-21G level of theory. The resulting structure is shown below, having C1 symmetry and a total energy of -231.69266 a.u.. As this is the lowest energy conformation of 1,5-hexadiene, the relative energy of each conformation can be found with the energy of this conformation as the reference. These have been shown in the table above.
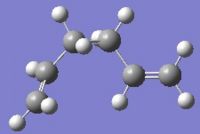 |
The structures above can be re-optimised with a higher level of theory to get more accurate structures and energies. In this case, the Ci anti conformer was re-optimised using the B3LYP method with the 6-31G* basis-set. The differences between the two optimisations can be seen in the tables below.
| Property | HFT/3-21G | B3LYP/6-31G* | Difference |
|---|---|---|---|
| Total Energy/a.u. | -231.69254 | -234.61171 | 2.92 |
| C=C bond length/pm | 132 | 133 | 1 |
| C-C bond length/pm | 155 | 155 | 0 |
| C(sp2)-C(sp3)/pm | 151 | 150 | 1 |
| C(1)-C(2)-C(3) bond angle/o | 124.8 | 125.3 | 0.5 |
| C(2)-C(3)-C(4) bond angle/o | 111 | 113 | 2 |
From this it can be seen that whilst there are some differences, the two structures are largely the same. However, the most important difference is that the conformer resulting from the higher level of theory has a lower total energy. As such, this is the structure that most closely resembles the stable Ci anti conformer. Thus, although the higher level of theory is more accurate at modelling the structure of 1,5-hexadiene, the HFT/3-21G level of theory is mostly sufficient for gaining the lowest energy structure.
A frequency analysis, at the same level of theory, can be carried out to ensure that the conformations gained by the optimisations are stable conformations, rather than transition states. If the vibrational analysis delivers a vibration with a negative frequency, an imaginary vibration, then the structure is a transition state. In fact, the vibrational analysis of the Ci anti conformation did not deliver any imaginary vibrations meaning that it is in fact a minimum energy conformation. A selection of the important vibrations for 1,5-hexadiene are shown below:
| Frequency/ cm-1 | Vibration | Intensity |
|---|---|---|
| 1734 |  |
18 |
| 3031 |  |
54 |
| 3081 |  |
36 |
| 3156 |  |
15 |
The frequencies delivered are within the normal range for C=C, the lowest frequency vibration, and C-H, the higher three vibrations, bond stretches. The agreement of the predicted spectrum with experiment can be judged better by using the GaussView program to predict the IR spectrum of 1,5-hexadiene from this vibrational analysis, and comparing it to an experimental IR spectrum. In this case the experimental IR spectrum is from the NIST/EPA Gas-Phase Infrared Database.
 |
 |
As can be seen, the computed IR spectrum fits closely the experimental one, especially in the stretching regions identified above. However, there is some discrepancy in the relative intensities of the peaks. This indicates that the B3LYP/6-31G* level of theory is quite accurate when it comes to calculating frequencies, but not so accurate in calculating intensities.
As well as giving information about the vibrations of 1,5-hexadiene, the vibrational analysis returns information about the energy of the molecule. This is particularly useful as the total energy returned in the summary of the calculations is that of the molecule on the potential energy surface of the optimisation. To make more meaningful comparisons with experimental data, the energy terms returned in the 'Thermochemistry section of the vibrational analysis output are shown below.
Sum of electronic and zero-point Energies = -234.469196 a.u. Sum of electronic and thermal Energies = -234.461849 a.u. Sum of electronic and thermal Enthalpies = -234.460905 a.u. Sum of electronic and thermal Free Energies = -234.500776 a.u.
Optimising the "Chair" and "Boat" Transition States
Whilst optimising the structure of the reactants and products of a reaction can be done quite easily and reliably with the molecular mechanics method, finding a transition state can not. However, these can be found using a number of techniques based on quantum mechanics calculations like those used above. In all cases, carrying out a vibrational analysis identifies the structure as a transition state by the presence of an imaginary frequency.
Chair Transition State
The first step in finding the transition state of the cope rearrangement was to have a guess at it's structure. This was done by optimising an allyl fragment at the HFT/3-21G level of theory. Two of these optimised fragments were used to approximate the chair conformation of cyclohexane, keeping the termini of the fragments around 220 pm away from each other.
Depending on how close this guess structure is to the transition state, two different methods can be employed to find it. The first of these is to carry out an optimisation and frequency analysis on the guess state at the HFT/3-21G level. This was done using the Opt+Freq option. However, instead of optimising to a minimum as would be done to find the lowest energy conformation of a molecule, it was optimised to a transition state using a Berny optimisation. The force constants were only calculated once, and the keywords Opt=noeigen were added to ensure that if more than one imaginary frequency is found the calculation does not crash.
The second is to freeze the fragments along the reaction coordinate whilst the optimisation is carried out, and then to perform the vibrational analysis. This was done by editing the redundant coordinates of the guess TS so the distance between the fragments is fixed at 220 pm. An optimisation was then carried out at the HFT/3-21G level. The redundant coordinates of the output were then edited to set the the bonds between the two fragments as Derivatives. An optimisation and frequency analysis was then carried out as in the previous method, but without the force constants being computed.
The structures returned by these two methods, and the differences between them can be seen below:
As can be seen freezing the molecule along the reaction coordinates yields more accurate results, with the total energy being slightly lower. However, the differences in the bond length and imaginary frequencies are not very significant as they are less than the accuracy of the level of theory used.
The imaginary frequency from the vibrational analysis corresponds to the formation of a new bond, as it is the molecule moving to a lower energy conformation. For the chair transition state this is -818 cm-1, with the distance between the allyl fragments being 202 pm.
Boat Transition State
Whilst these two methods were adequate to find the chair transition state, a third method was employed to find the boat transition state. This was the QST2 method. In order to do this, two molecules of 1,5-hexadiene were used in the input file. It was necessary to number the molecules so that one corresponded to the reactant and one to the product. The input was then optimised and a frequency calculation carried out with the QST2 method.
However, this failed to find the boat transition state, instead once again finding a chair shaped structure with bonds between the termini. For the QST2 method to work, the orientations of the reactant and product must be altered to resemble the boat structure more closely. This was done by changing the C(2)-C(3)-C(4)-C(5) angle to 100o in both molecules. The optimisation and frequency analysis was then carried out once again. This delivered the transition state below:
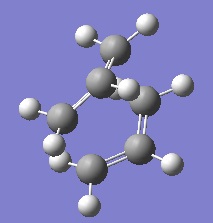 |
The distance between the termini of the allyl fragments is 214 pm, the imaginary frequency is -840 cm-1, and the total energy of the boat transition state is -231.6028 a.u..
The QST2 method used in this case was only useful after the geometries of the reactants and products were changed to resemble more closely the suspected transition state structure. However, the QST3 method allows a guess structure of the transition state to be included in the calculations, which would mean that the conformation of the products and reactants does not need to be changed.
Intrinsic Reaction Coordinate
Although the transition states have been found using the techniques above, the conformations of 1,5-hexadiene that are formed as a result of these transition states have not been found. There is a method that can do this however, by finding the lowest energy path from the transition to the local energy minimum. This is the intrinsic reaction coordinate (IRC) method, and works by altering the geometry of the transition state in small steps in the direction on the potential energy surface that has the steepest gradient.
This was done for the chair transition state, selecting the option to only carry out the IRC calculation in the forwards direction, as the molecule is symmetric along the reaction coordinate. The force constants were only calculated once, and 50 points along the reaction coordinate were calculated. The results of this can be seen below.
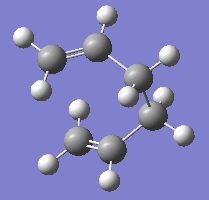 |
 |
 |
From the energy profile we can see the IRC calculations moving towards lower energy structures from the high energy transition state. The RMS gradient of the IRC analysis however indicates that the calculation did not find the lowest energy structure, as the gradient does not reach zero. This can be resolved in three ways. The first is to take the final step in the IRC calculation shown above and optimise this using a higher level of theory. Whilst this is the fastest option, it may find a local minimum that is not the overall energy minimum. The second option is to restart the IRC calculations using more points. This is more reliable than the first, but if too many points are needed the calculation can end up going in the wrong direction. Finally, the IRC analysis can be repeated but this time calculating the force constants at each step. Although this is the most reliable method, it is also the most computationally demanding. For these reasons, it was assumed that the final step of the IRC analysis already carried out was close to the energy minimum, and an optimisation was carried out at the B3LYP/6-31G* level of theory.
The same IRC analysis was carried out for the boat transition state. The results of this are shown below.
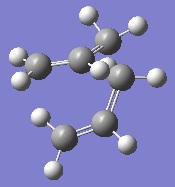 |
 |
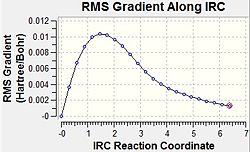 |
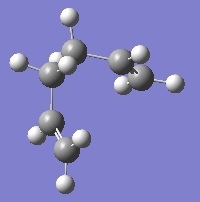
As can be seen, once again the IRC analysis did not complete. For this reason, an optimisation was carried out again at the B3LYP/6-31G* level of theory. The two products of the chair and boat transition states optimised at this level can be seen below.
 |
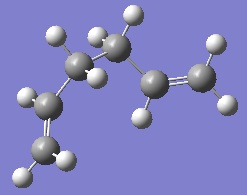 |
The result of the chair IRC is a gauche conformation of 1,5-hexadiene with C2 symmetry. In contrast, the product formed by the boat transition state is the lower energy gauche conformation with C1 symmetry. In fact, this is the conformation of 1,5-hexadiene that was identified as having the lowest energy during the optimisation of the reactants above.
This suggests that the cope rearrangement of 1,5-hexadiene through the boat transition state is thermodynamically favoured, as the product is lower in energy.
Activation Energies
As well as identifying the transition states, the vibrational analyses carried out above can give useful information about the energies of the transition states, as was seen for the reactants in the first part. To gain this information in an accurate way, the final structures of the transition states gained at the HFT/3-21G level of theory were re-optimised and the vibrational analysis carried out at the higher B3LYP/6-31G* level of theory. In the two tables below, the transition state structures at each level of theory have been compared.
From this it can be seen that whilst the geometry of the two transition states remains largely the same between the two levels of theory, the imaginary frequencies are much higher with the higher level of theory. The most startling result is that the imaginary frequency of the boat transition state at the B3LYP/6-31G* level is actually higher in energy than the imaginary frequency of the chair TS.
The different energies returned from the vibrational analyses of the transition states can be compared to those returned for the reactant at both levels of theory.
| Energy | HFT/3-21G | B3LYP/6-31G* | ||||
|---|---|---|---|---|---|---|
| Reactant | Chair TS | Boat TS | Reactant | Chair TS | Boat TS | |
| Total Energy/a.u. | ||||||
| Sum of Electronic and Zero Point Energy (0K)/a.u. | ||||||
| Sum of Electronic and Thermal Energies (298.15K)/a.u. | ||||||
| Method | HFT/3-21G | B3LYP/6-31G* | ||
|---|---|---|---|---|
| Temperature/K | 0 | 298.15 | 0 | 298.15 |
| Activation Energy (Chair)/ kcalmol-1 | 45.7 | 44.1 | 34.3 | 33.1 |
| Activation Energy (Boat)/ kcalmol-1 | 55.6 | 51.3 | 42.0 | 41.3 |
At 0K, the experimental values[1] are 33.5 ± 0.5 kcal/mol for the chair conformation and 44.7 ± 2.0 kcal/mol for the boat conformation. Thus the B3LYP/6-31G* level of theory is sufficient to get close agreement with experimental values.
The Diels Alder Cycloaddition
A Diels Alder cycloaddition is [4+2] cycloaddition, involving the formation of two new sigma bonds from the п orbitals of a diene and dieneophile. These cycloadditions occur in a concerted pericyclic way, but only if the number of п-electrons and the symmetry of the frontier orbitals involved satisfy certain rules. If these rules are satisfied the reaction is said to be allowed, and if they are broken it is said to be forbidden.
The symmetry requirement of the cycloaddition means that the HOMO of one reactant can only overlap with the LUMO of the other if their symmetry matches. If no overlap occurs due to a mismatch in symmetry, then no HOMO-LUMO interaction occurs and the reaction is forbidden.
Altering the substituent on the dienophile will alter the п-orbitals on it. This in turn will affect the regiochemistry of the reaction. This can be modelled using the quantum mechanics based methods as above, and will be done in the following section for a prototypical reaction, as well as for reactions involving substituted dienes and dienophiles where secondary orbital interactions are possible.
Prototype Reaction: Ethylene and Butadiene
 |

The prototypical Diels Alder cycloaddition is between ethylene and butadiene, with butadiene as the unsubstituted diene and ethylene as the dieneophile.
In this reaction, butadiene must be in cis-conformation, making it belong to the C2v point group. As ethylene belongs to the D2h point group, both are symmetric about a σv plane of symmetry. The frontier orbitals of these reactants will be symmetric (s) or antisymmetric (a). These orbitals can be predicted qualitatively by the linear combination of atomic orbitals (LCAO) method. In this case, the frontier orbitals will be created by combining p-orbitals to create MOs with either π or π* symmetry. As can be seen, the predicted HOMO of cis-butadiene is antisymmetric with respect to this plane of symmetry, whilst its LUMO is symmetric. On the other hand, the HOMO of ethylene is symmetric whilst its LUMO is antisymmetric. This suggests that either the HOMO of cis-butadiene interacts with the LUMO of ethylene, or the HOMO of ethylene with the LUMO of cis-butadiene:
 |
 |
 |
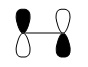 |
The frontier orbitals of the reactants were found by optimising the structures using the semi-empirical AM1 method in Gaussian. The resultant orbitals can be seen below with an iso-value of 0.05.
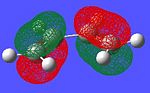 |
-9.33 eV |  |
+0.46 eV |  |
-10.53 eV | 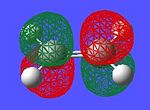 |
+1.41 eV |
As can be seen, the symmetry of the frontier orbitals predicted was in fact correct. Furthermore, it can be seen that the HOMO and LUMO of butadiene are formed by the combination of the π and π* orbitals of ethylene, and that the qualitative LCAO method used above is actually quite accurate in predicting the shape of the resultant MOs in this case. However, to test which HOMO interacts with which LUMO, the transition state of the cycloaddition must be computed, as was done for the cope rearrangement above.
This was done by guessing a structure for the transition state based upon an envelope geometry. This was optimised using the redundant coordinate editor as before to freeze the reaction coordinate. An optimisation and frequency analysis was then carried out on this optimised structure to gain the optimised transition state, and ensure that it is in fact the transition state.
The transition state was indeed found, as indicated by the presence of an imaginary frequency in the vibrational analysis. These can be seen below along with the HOMO and LUMO for the transition state (Link to file: [1]).
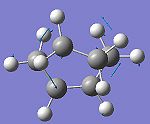
The imaginary frequency shown above confirms that this is the transition state for the cycloaddition, as the vectors indicate the formation of a bond between the terminal cis-butadiene carbons and the ethylene carbons. These also indicate that the formation of these two bonds is synchronous, supporting the observation that the Diels Alder cycloaddition occurs in a concerted fashion. The lowest positive frequency for the transition state, at 147 cm-1, corresponds to the wagging of the ethylene molecule in relation to the cis-butadiene molecule. This obviously does not to correspond to any bond forming or breaking.
The HOMO of the transition state shows the formation of two σ-bonds by the overlap of the antisymmetric HOMO orbital of cis-butadiene with the antisymmetric LUMO of ethylene. The LUMO however can be seen to be the overlap of the symmetric HOMO of ethylene with the symmetric LUMO of cis-butadiene. As this is close to zero, this orbital can be seen as a non-bonding MO. The overlap of these orbitals is allowed as they have the same symmetry with respect to the mirror plane described above.
The two partly formed C-C σ-bonds are both 2.12 A long. The C-C(ethylene) bond length is 138 pm, as is the length of the two terminal C-C bonds in the cis-butadiene molecule. The middle C-C bond in the cis-butadiene molecule is 1.40 A. The literature values found were 1.34 A[2] for the average sp2 C-C bond, and 1.54 A[3] for the average sp3 C-C bond. Thus, the two partly formed σ-bonds are significantly longer than a normal sp3 C-C bond. Furthermore, all of the other C-C bonds are somewhere inbetween the two literature values, showing that the π-bonding of the reactants is being disrupted and the hybridisation of the carbons is changing.
Reaction between Cyclohexa-1,3-diene and Maleic Anhydride
In the prototypical Diels Alder reaction modelled above, there are no issues with selectivity. However, when the reactants are both cyclic, regiostereochemical implications ensue. In such cycloadditions, either the exo or endo product can be formed. In some cases, such as the reaction of cyclopentadiene with maleic anhydride[4], a preference for the exo product has been observed, which has been explained by the formation of secondary orbital interactions[5].
These secondary orbital interactions (SOIs) can be seen as the overlap of orbitals that are not involved in the formation of the two new σ-bonds. As can be seen, these are only possible when the reactants approach each other so as to form the endo-isomer rather than the exo-isomer. Thus, where SOIs occur, the endo-transition state is stabilised, thus lowering the kinetic barrier to the formation of the endo-product. However, the validity of invoking SOIs to explain the preference for endo-isomers in these Diels Alder reactions has been debated, with some evidence suggesting it can also be explained by dispersion forces alone[6].
Despite this, evidence has gathered that suggests these do in fact exist in many cases[7], including the cycloaddition of cyclopentadiene with maleic anhydride[8].

In this part, the reaction of cyclohexa-1,3-diene with maleic anhydride will be investigated. As this is very similar to the reaction of cyclopentadiene with maleic anhydride, it is very reasonable that some sort of SOI will be seen for this reaction and that the endo-product will be preferred.
The semi-empirical AM1 method was once again used to model the HOMO and LUMO of the reactants. These can be seen below.
 |
 |
 |
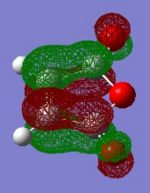 |
From the above it can be seen that the most likely orbitals involved in the reaction are the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride. As such, it is likely that in the endo transition state, SOIs will occur between the C-C π-orbitals in the HOMO of cyclohexa-1,3-diene and the C=O π*-orbitals in the LUMO of maleic anhydride. In the drawings below the bond-forming interactions have been represented as dashed lines, whilst the SOIs are bold arrows.
 |
 |
To investigate this, the transition states were modelled using the frozen coordinate method outline above. This was done using the semi-empirical AM1 level of theory once again. The resultant transition states can be seen below, with the imaginary frequency that confirms that they are in fact transition states (Link to files: Endo and Exo.
 |
 |
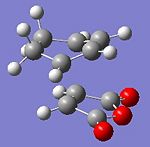 |
 |
From the above, it can be seen that both transition states were found, as the imaginary frequencies correspond to bond forming vibrations. The exo-isomer has a higher total energy than the endo-isomer, suggesting that it may be thermodynamically, as well as kinetically, favoured.
The frontier molecular orbitals were also visualised, and these can be seen below.
 |
 |
 |
 |
All of the above orbitals are antisymmetric with respect to the mirror plane described before, as a result of being formed from the antisymmetric orbitals of the reactants. In the HOMOs of both transition states, the partially formed σ-bonds can be seen. If any SOI was present in these molecular orbitals, a region of delocalised electron density would be expected between the carbonyl carbon and the cyclohexa-1,3-diene π-orbitals on each side of the transition state. However, as can be seen, in the HOMO of each this delocalisation is not present at all.
This suggests that there is no stabilisation due to secondary orbital interactions. Although this may well be the case, it could also be a result of the low-level of theory used. Furthermore, the size of the interactions may be too small to visualise, this being made even worse if the method used is largely innacurate. This is supported by the fact that the SOIs reported for the reaction between cyclopentadiene and maleic anhydride are small, so these may well be too[9].
Conclusion
From the above exercises, it can be seen that methods based on quantum mechanics can model transition states of reactions with a good degree of accuracy. This was seen in the first exercise, with the values gained for the activation energies agreeing well with the experimental data. Furthermore, these methods can be used to elucidate the mechanism of the reaction, with properties such as the imaginary frequency and the molecular orbitals allowing insight into this.
References
- ↑ Wiest, O.; Black, K.A.; Houk, K.N., J. Am. Chem. Soc., 1994, 116, 10336-10337 DOI:10.1021/ja00101a078
- ↑ Stoicheff, B.P., Tetrahedron, 1962, 17, 135-145 DOI:10.1016/S0040-4020(01)99013-1
- ↑ Bartell, L.S., J. Am. Chem. Soc., 1959, 81 (14), 3497-3498 DOI:10.1021/ja01523a002
- ↑ Stephenson, L.M.; Smith, D.E.; Current, S.P., J. Org. Chem., 1982, 47 (21), 4170-4171 DOI:10.1021/jo00142a035
- ↑ Clayden, Greeves, Warren, Wothers, Organic Chemistry, 2001, Oxford University Press, Oxford, pp916-7
- ↑ Garcia, J.I.; Mayoral, J.A.; Salvatella, L., Acc. Chem. res., 2000, 33 (10), 658-664 DOI:10.1021/ar0000152
- ↑ Wannere, C.S.; Paul, A.; Herges, R.; Houk, K.N.; Schaefer, H.F.; Schleyer, P.v.R., J. Comp. Chem., 2007, 28 (1), 344-361 DOI:10.1002/jcc.20532
- ↑ Arrieta, A.; Cossio, F.P.; Lecea, B., J. Org. Chem., 2001, 66 (18), 6178-6180 DOI:10.1021/jo0158478
- ↑ Arrieta, A.; Cossio, F.P.; Lecea, B., J. Org. Chem., 2001, 66 (18), 6178-6180 DOI:10.1021/jo0158478