Rep:Mod:bw08firstreport
Module 1: Organic
The Value of Computational Chemistry
Computational chemistry is a multidisciplinary area of science transcending traditional barriers sparating biology, chemistry, physics and mathematics. As theory can help to rationalize experimental observation, provide information not amenable to experimentation and even make predictions concerning the outcome of future experiments, it has become widely accepted by experimental scientists as a valuable supplement to their existing studies. One aspect of applied theory involves molecular simulations at the atomic level, which is sometimes called “molecular modeling”.
Molecular Modeling
Two broad categories of chemical modeling may be considered: macroscopic models and microscopic models. Macroscopic models consider, for example, rates of uptake of material and kinetics of transport, without consideration of structural features of the individual molecules. In contrast, microscopic models (often called atomistic models) usually take full account all the atoms in the system.
Microscopic, atomistic modelling is done in two ways: using fitting procedures or by applying theory from first principle. The fitting procedures are an attempt to rationalize connections between molecular structure and physiochemical properties (quantitative structure property relationships, QSPR) or with biological response (quantitative structure activity relationships). This type of modelling requires use of existing data to create the model and then allows interpolation or extrapolation of new properties of as yet unknown molecules within that same class of compounds.
The second kind of atomistic modelling applies theory, usually from first principles. Three commonly used modelling techniques involve the use of quantum mechanics, molecular mechanics or molecular dynamics. During the first part of this investigation, molecular mechanics was used to carry out the calculations.
Molecular Mechanics and Force Fields- Key Equation and Principles
These five equations have the following meanings:
- The bond stretching term (quadratic function), where K is the bond force constant.
- The bond angle term (quadratic function).
- The dihedral term, describing the torsion around a bond; in general this is low for a single and triple bond, high for a double bond, medium for a delocalized bond. V is related to the rotation barrier about the bond.
- Non-bonded term.
- A hydrogen bond term.
The underlying philosophy of molecular mechanics is to view a molecule as a collection of particles (nuclei) held together by some sort of elastic forces (electrons). In contrast to quantum mechanics where electrons are explicitly treated, in molecular mechanics the electrons are implicitly treated and, thus, it is not possible to assess bond-making or bond-breaking events as is possible with quantum mechanical methods, unless special functions are used. Hence molecular mechanics is used to reliably and quickly predict the structures of small- to medium-sized molecules, or to evaluate very large molecular assemblies. [1]
Notable Limitations of the Molecular Mechanics Approach
Firstly, the method uses data from well characterised molecules. Hence this technique is interpolative rather than extrapolative and it cannot deviate far from commonly observed chemistry. This results in difficulty in assessing the kinetic control of a reaction, as that requires parameters of the transition state. It is also challenging to model new molecules with unusual bonding, for these reasons mentioned, therefore complete quantum mechanical treatment of the system is necessary. Molecular orbital theory, another quantum mechanical method, may also have to be turned to for analysis of molecular properties such as stereoelectronic effects, aromaticity and hyperconjugation. Metal ions are also more difficult to handle using this type of model. Finally, this method involves modeling in the gas phase, which may ignore vital electronic interactions taking place with solvent molecules during a reaction, which can have a large impact on chemical reactivity.
Hydrogenation of Cyclopentadiene Dimer
Dimerisation of Cyclopentadiene
At room temperature, cyclopentadiene will slowly react with itself to form dicyclopentadiene. This reaction is an example of a [4π+2π] cycloaddition (when referring to the number of atoms in the system), or a [3+2] cycloaddition (when referring to the number of atoms involved). This reaction proceeds via a Huckel transition state (4n+2) with suprafacial topology.
There is a high degree of stereospecificity in this reaction. Two possible compounds can be formed, the endo- or exo- product. The overall reaction is shown below.
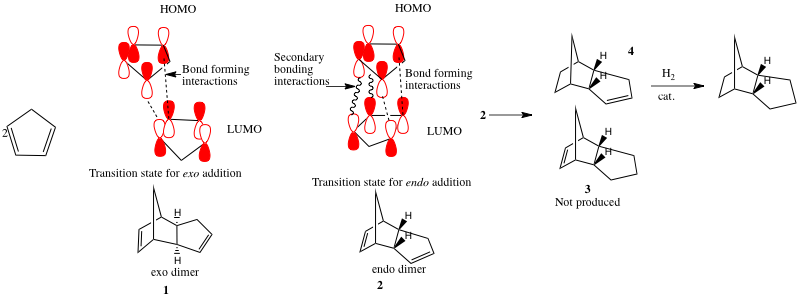
The total energy of each product was computed as is shown in the table below, alongside the individual contributions.
| Energy parameter | Endo energy (kcal mol-1) | Exo energy (kcal mol-1) |
|---|---|---|
| Stretch | 1.255 | 1.281 |
| Bend | 20.826 | 20.570 |
| Stretch-Bend | -0.834 | -0.837 |
| Torsion | 9.512 | 7.667 |
| Non-1,4 VDW | -1.499 | -1.415 |
| 1,4 VDW | 4.310 | 4.236 |
| Dipole/Dipole | 0.445 | 0.378 |
| Total energy | 34.0136 | 31.8796 |
This indicates that the endo dimer has an energy which is ~2kcal mol-1 higher than the exo dimer. This is consistent with the ' endo rule' for Diels Alder reactions. In general the two hydrogen atoms bridding the two cyclic structures must be cis in both products, but there are two possible products which obey this rule. These are called the endo and exo products. Although the endo product is higher in energy, it is produced under these kinetically controlled conditions, as the transition state leading to this product is stabilised relative to that leading to the exo product. This is represented in the diagram above.
Another way of looking at this result is by recognizing the negative entropy of activation as two molecules combine to produce one. A very precise orbital orientation is needed for the two bonds to form at once, which is assisted by the through space HOMO/LUMO bonding interaction.
Under a high enough temperature, however, the more thermodynamically stable product (i.e exo) will dominate the product mixture. This is expected as there is enough energy to pass through each of the transition states, so the most stable product will be produced.
Hydrogenation of Endo Dimer
Hydrogenation of the endo cyclopentadiene tends to give a dihydro derivative; a tetrahydro derivative is only formed under prolonged hydrogenation conditions.
By analysing the energies of the two dihydro derivatives of the endo dimer this enables an informed prediction as to which C-C double bond will be hydrogenated first.
| Type of Energy | Molecule 3 /kcal mol-1 | Molecule 4 /kcal mol-1 | Energy Difference /kcal mol-1 |
| Stretch | 1.24 | 1.10 | 0.14 |
| Bend | 18.97 | 14.51 | 4.46 |
| Stretch-Bend | -0.76 | -0.55 | -0.21 |
| Torsion | 12.15 | 12.50 | -0.35 |
| Non-1,4 VDW | -1.56 | -1.51 | -0.05 |
| 1,4 VDW | 5.73 | 4.51 | 1.22 |
| Dipole/dipole | 0.16 | 0.14 | 0.02 |
| Total Energy | 35.93 | 31.51 | 4.42 |
Hydrogenation product 4 is more stable than compound 3 by about 4 kcal mol-1), suggesting that the facility of hydrogenation is greater when compound 3 is formed. This prediction is made purely on a thermodynamic analysis of both compounds. This suggests that the double bond in the bridged ring is easier to hydrogenate than the unbridged double bond. Each compound has similar contributions to the total energy from the stretching, torsion, Van der Waals and hydrogen bonding energy terms, whilst the largest difference is observed between the bending contributions ( 4.5 kcal mol-1).
The bending energy of molecule 3 is much higher than in molecule 4, showing that the structure of molecule 3 is relatively unstable with a large deviation of bond angles from the ideal molecule. Furthermore, the C=C bond is found closer to the tertiary carbon atom in molecule 3 than in molecule 4. This shows that there is an increase in steric hindrance and strain in molecule 3. Therefore, the rotation of the bond is restricted and the increase in bending would lead to the relief of strain in the norbornene.
Finally, a comparison is made between the H-C=C and C-C=C bond angles found in both molecules as it is closely linked to the points outlined above. The ideal angle for a sp2 hybridized carbon is 120°. Consider the H-C=C bond angles in molecules 3 and 4, which are 108° and 113° respectively. The greater reduction of H-C=C bond angle in compound 3 indicates a higher level of strain relative to compound 4, as it is the furthest from the ideal value of 120°.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Part (a)
There has been widespread interest in the regio- and enantioselective conversion of 2-substituted nicotinic acid derivatives A into C(4) substituted dihydropyridines B and other compounds. Consequently, synthetic intermediates of type B should be of use in the enantioselective construction of alkaloids containing the piperidine ring system.
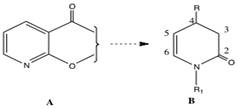
A large number of studies concerned with the addition of carbon nucleophiles to pyridines have been reported. Both the “free base” and the activated pyridinium salts undergo 1,2-, 1,4- and 1-6 additions.[2]
The first reaction investigated in this area involves the optically active derivative of prolinol (5) which undergoes a nucleophilic addition with methyl magnesium iodide to alkylate the pyridine ring in the 4-position, with the absolute stereochemistry shown in 6. Heterocycle 5 is prepared in 86% yield from 2-chloronicotinic acid and L-prolinol.[3] It is also noteworthy that the alkylithium reagents are nearly regio- and stereo- random. The high regio- and stereo- selectivity of this reaction has been proposed to result from initial coordination between the Grignard reagent and the amide oxygen atom, as shown below.

Conjugate delivery of the methyl group from magnesium to C(4) of the pyridine ring generates a magnesium enolate, which then goes on to produce 6.[4]
Dreiding stereomodels indicate that there is almost no flexibility in the seven membered ring of 5. Two conformational minima were found to be possible. One of these has the amide carbonyl group above the plane of the pyridine ring anti to the hydrogen atom at the chiral centre; the second has the carbonyl group and pyridine ring coplanar. Most importantly, no conformation was found to exist which positions the amide carbonyl group below the plane of the pyridine ring.
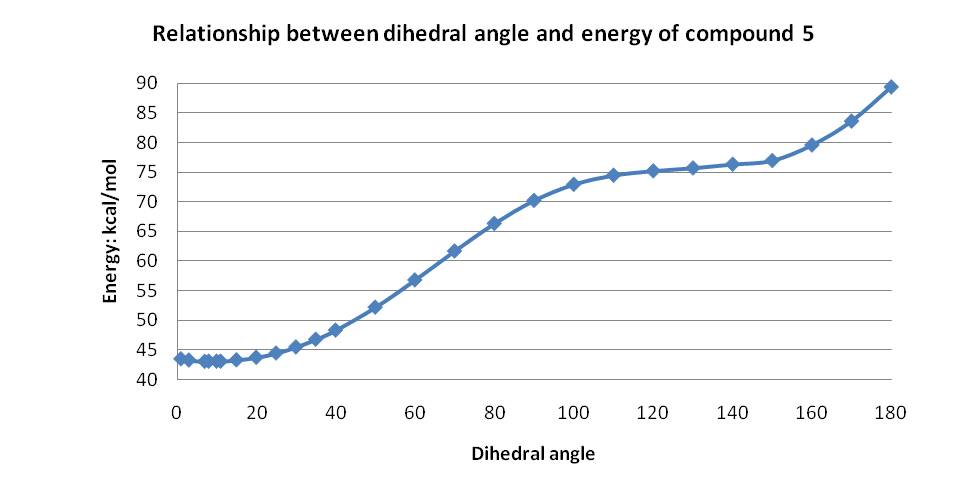
Using this information, the dihedral angle between the bonds highlighted in 5 above was varied in order to obtain the lowest energy. Initially the MM2 force field was used and the dihedral angle was tested for 0°, 5°, 10° and 20°. Energies of a range of conformations where the amide carbonyl group is above the plane of the pyridine ring and syn to the hydrogen atom at the chiral centre were also found, but as expected all had energies above those where the amide carbonyl group above the plane of the pyridine ring. This clearly indicated the preferred conformation has a dihedral angle of about 10°, but complete analysis was carried out from 0-180° degrees giving the results shown in the graph below.

Minor products resulting from Grignard reactions of this kind and random addition products isolated when alkyllithium reagents are used are expected to derive from pathways not involving the type of chelation control shown in 5a.
As the MM2 molecular mechanics approach encounters difficulties when dealing with compounds containing a positively charged nitrogen atom, the structure of compound 5 was also optimised using MMFF94 and MOPAC PM6 methods. The results are shown below.
| Method | Dihedral angle | Energy (kcal mol-1) |
|---|---|---|
| MMFF94 | 20.9o | 57.5 |
| MOPAC PM6 | 20.5o | 93.6 (heat of formation) |
These results showed higher overall energies for the ‘lowest energy’ conformations, but the dihedral angles obtained of 20.15o and 20.60o, respectively, are in good agreement with each other. In each case, these models show the lowest energy conformation as having the carbonyl group above the plane of the ring, reinforcing the proposed mechanism to account for the stereochemistry of the product.
Even higher selectivity and yield in this reaction type is expected and has been reported when bulkier reagents such as PhMgBr is used, promoting addition of the alkyl or aryl group anti to the hydrogen atom at the chiral centre.
Part (b)
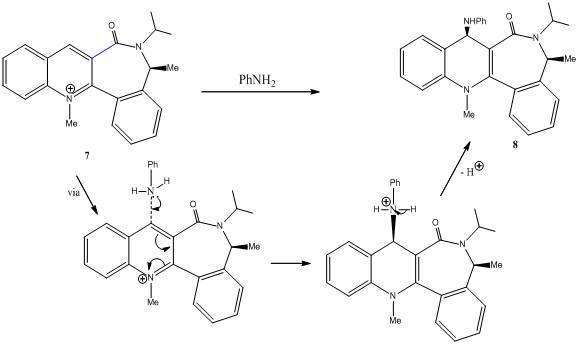
Several new synthetic tools have been developed from investigation of potential biomimetic NAD+ models as ‘nucleophile-transferring agents’. Compound 7 is an example of an axially chiral quinolinium salt. Nucleophilic addition of phenylamine to 7 yields 8 as the single diastereoisomer. The high level of selectivity is also observed when benzylamine or piperidine is used as the addition reagent. 2D-NOESY experiements, showing dipolar coupling between the methyl group of the lactam moiety and the methylene protons adjacent to the nitrogen of the amine confirm that both amines react on the opposite face with respect to the C=O lactam.
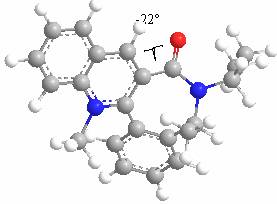
Using this information, MM2 analysis of the dihedral angle was carried out. The lowest energy was expected to be recorded when the C=O bond is below the plane of the pyridinium ring (negative dihedral angle). For completeness, energies of the conformations having the C=O bond above the plane of the ring were also computed.

This shows a minimum energy conformation when the dihedral angle is approximately -20o.
Results from MMFF94 and PM6 MOPAC analysis show a dihedral angle of approximately 40o below the plane of the quinolinium ring. The MMFF94 and PM6 results show quite high energies but they are in good agreement:
| Method | Dihedral angle | Energy (kcal mol-1) |
|---|---|---|
| MMFF94 | -40.9o | 99.8 |
| MOPAC PM6 | -43.5o | 156.4 (heat of formation) |
These results are extremely different from those obtained using the MM2 analysis. Again, the MM2 results are not particularly accurate due to its inability to correctly process the N+ of the ring.(N.B. The MMFF94 force field does not permit a dihedral angle to be inputted, in order to calculate the energy of such a geometry.)
The excellent diasterofacial selectivity observed orginiates from steric control exerted by the carbonyl lactam. The results compiled by Leleu et al. suggest that the chiral axis defined by the C3-C=O bond (highlighted in blue in compound 7) is the main configurational element governing the stereoselectivity of this nucleophilic addition. This element plays a key role in terms of diastereoselectivity, during the ‘anchoring step’ of the amine on compound 7, in which case the methyl group attached to the chiral carbon acts as the ‘chiral inducer’. [5]
The incoming nucleophile (phenylamine is this case) therefore reacts on the opposite face (anti) to the C=O lactam, giving the product 8.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
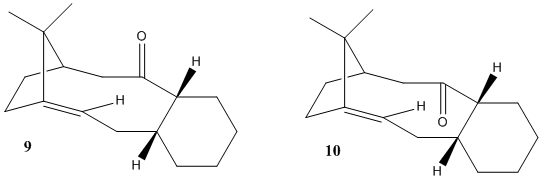
Atropisomerism is the distinction arising between two molecules that results due to restricted rotation about a single bond, usually due to high steric demand removing the usually free rotation.[6]
During this section the energy of molecules 9 and 10 will be computed and the reason for the slow rate of hydrogenation of the C=C bond will be explored. The geometries of each compound were optimized using MM2-forcefield to determine the most stable isomer. Many individual geometry modifications were made by moving the carbonyl group and changing the cyclohexane ring to the preferred chair conformation.
| Energy of Molecule 9/Kcal/mol | Energy of molecule 10/Kcal/mol |
|---|---|
| 48.89 | 44.31 |
| Bend Energy/Kcal/mol | Stretch Energy/Kcal/mol | Torsion Energy/Kcal/mol | VDW Energy/Kcal/mol |
|---|---|---|---|
| 15.84 | 2.68 | 18.17 | 12.20 |
| Bend Energy/Kcal/mol | Stretch Energy/Kcal/mol | Torsion Energy/Kcal/mol | VDW Energy/Kcal/mol |
|---|---|---|---|
| 10.69 | 2.53 | 19.79 | 11.30 |
On comparing the energy distribution of both compounds, the largest energy difference is in the bending energy as compound 10 has approximately 5Kcal/mol less energy in this mode. This reflects the large deviation from ideality in compound 9 , and modeling carried out on both compounds indicates that the main source of this energy change is the change ingeometry of the carbonyl group. Both compounds adopt a chair conformation in the cyclohexane ring: in 9 the carbonyl is on the ‘top’ face. In this position there is poor overlap between the low energy C=O σ* orbital and the bonding sigma C-H orbitals adjacent to it due to incorrect orbital orientation. Whereas in 10 the carbonyl is on the ‘bottom’ face, leading to a better orbital orientation between the bonding and anti-bonding orbitals resulting in a larger energy of stabilization, lowering the total energy of 10 below that of 9.
Alkene Reactivity
Given that 10 is the most stable isomer hydrogenation is modeled on this compound. The results are shown below.
| Energy of Molecule 10/Kcal/mol | Energy of hydrogenation product/Kcal/mol |
|---|---|
| 44.31 | 53.09 |
| Bend Energy/Kcal/mol | Stretch Energy/Kcal/mol | Torsion Energy/Kcal/mol | VDW Energy/Kcal/mol |
|---|---|---|---|
| 10.69 | 2.53 | 19.79 | 11.30 |
| Bend Energy/Kcal/mol | Stretch Energy/Kcal/mol | Torsion Energy/Kcal/mol | VDW Energy/Kcal/mol |
|---|---|---|---|
| 13.49 | 2.73 | 22.04 | 14.83 |
As the alkane produced is higher in energy than the starting alkene 10, the transition state (governing kinetics and reaction rate) leading to the product is product-like and therefore also highly strained, therefore hydrogenation is not expected to occur.
Hyperstable alkenes
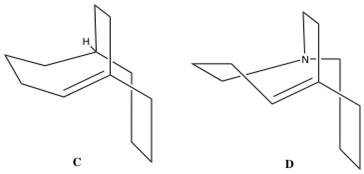
Bridgehead olefins have fascinated chemists ever since Bredt noted that double bonds avoid the ring junctions in camphane and pinane systems. [7] Bredt then formulated the empirical observation that states a double bond cannot be placed at the bridegehead of a bridged ring system unless the rings are large enough. Bredt’s rule is a consequence of the fact that having a double bond on a bridgehead would be equivalent to having a ‘‘trans’’double bond on a ring, which is impossible for small rings due to ring strain, and angle strain in particular. Hence it is important to remember that bridgehead alkenes are not necessarily hyperstable themselves, as some of these compounds can not even be made.[8]
Maier and Schleyer observed that the reverse is expected in medium-size polycyclic ring systems where bridgehead double bonds may actually be preferred. These ‘hyperstable alkenes’ have ‘’negative’’ olefin strain energies (OSE): the strain energy of the alkene is less than that of the parent hydrocarbon. A qualitative correlation was found from calculations using MM1 force field OSE values, which measure the thermodynamic driving force towards reaction, and experimentally observed stabilities and reactivites.[9] Due to their negative OSE values, hyperstable bridgehead alkenes have enthalpies of hydrogenation lower than normal (i.e. the values found for acyclic alkenes with the same degree of substitution); these enthalpies are even lower than those of medium size ring cycloalkenes.[10]
Several hyperstable bridgehead alkenes were reported shortly after Maier and Schleyer’s paper.[11] The predicted hyperstability of bridehead hyperstability of bridgehead alkenes in medium ring systems was first experimentally confirmed by Meifere et al.’s observations that bicyclo[4.4.2]dodeca-1-ene (C) resists hydrogenation. The hyperstable bridgehead alkene 1-azacyclo[4.4.4]dodeca-5-ene (D), which showed a strong intramolecular N-olefin interaction by photoelectron spectroscopy, was calculated by Alder et al. to have an enthalpy of hydrogenation of only 7.6 kcal/mol.
Modelling Using Semi-empirical Molecular Orbital Theory
In this section secondary orbital interactions will be taken into account in order to predict and explain chemical reactivity. By considering key occupied and unoccupied molecular orbitals, an insight will be gained into how electrons are distributed between these orbitals and how this impacts bonding and spectroscopic observations.
Regioselective Addition of Dichlorocarbene
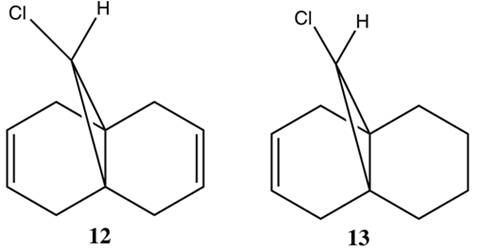
Compound 12 is a diene which can potentially react with electrophiles such as dichlorocarbene and peracids such as mCPBA at the double bond syn or anti to the C-Cl bond. A research group working on cycloproparene chemistry had to synthesise epimeric trichloride 14, which was done using the procedure below. [12]
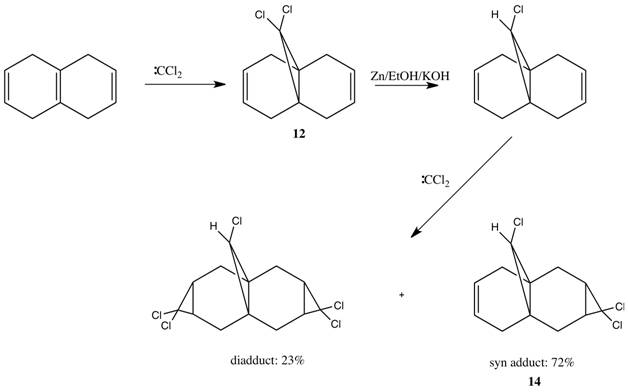
This work discovered a remarkably high pi-selective addition to the unsymmetrical diene 14. The results are consistent with a depletion of electron density from the pi-bond anti to the chlorine atom such that electrophilic addition occurs syn to this atom.[13]
In this rigid system free from steric differentiation, regioselection could arise from either orbital or electrostatic control or from specific factors present only in the transition state.[14] The Cieplak orbital model cannot be used in order to distinguish between the two alkene groups in 12 since they share common antiperiplanar sigma orbitals. Electrostatic π-facial asymmetry was proposed to account for the chiral discriminatory behaviour of derivatives of 12, and similar asymmetry in the calculated PM3 electrostatic potential (MEP) of 12 was noted.[15]This was explained by antiperiplanar stabilizing interactions between the Cl-C σ* orbital and the occupied exo pi-orbital, proposed to render the endo double bond more nucleophilic in both a frontier orbital and electrostatic manner. A major prediction arising from this analysis was that the Cl-C σ* exo π-orbital interaction would result in a strong geometric distortion of the exo double bond towards the bridgehead carbon.
Although 12 is a liquid at room temperature, verification of the crystal structure of 12 was performed by Rzepa, using low temperature crystallization and data collection. The results confirmed the predicted distortion, as the distance between either of the two anti (or exo) double bond carbon atoms and the central bridgehead carbon was measured to be 0.24 Angstroms (7%) shorter than the analogous endo distance. The molecular orbitals controlling the observed regioselectivity are shown below.
The HOMO indicates a large region of π electron density at the double bond 'syn' to the chlorine atom, encouraging electrophilic attack at this position. The anti double bond's π orbital correlates to the HOMO-1, which is perfectly set up for overlap with the σ* C-Cl orbital, found in LUMO + 2.
| Molecular orbital | Electron density distribution |
|---|---|
| HOMO-1 |  |
| HOMO | 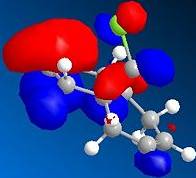 |
| LUMO | 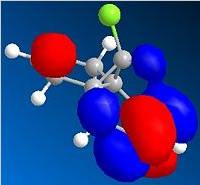 |
| LUMO+1 | 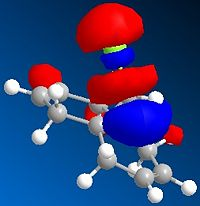 |
A B3LYP/6-31G(d,p) Gaussian calculation enabled the comparison of C-Cl and C=C frequencies, giving the results below.
This shows a large increase in C-Cl stretching frequency in 12 compared to the monalkene 13. This is due to the reasons outlined above: strong interaction between the anti π bond with the C-Cl σ* resulting in a reduction of the C-Cl bond strength and hence a lengthening of this bond. This interaction also leads to a reduction of electron density in the anti π bond, seen in the smaller vibrational frequency relative to the frequency of the syn double bond. As the vibrational frequency of the syn double bond is relatively unchanged between the two compounds, this confirms that it is unaffected by the chloro substituent.
Further Explorations and Confirmations
Furthermore, Rzepa found that antiperiplanar overlap with the Cl-C σ* (LUMO + 2) orbital results in the exo π-orbital (HOMO - 1) being stabilized by 0.08eV relative to the endo pi-orbital (HOMO). The (HOMO – 1) is also highly delocalized having significant components on the π-type cyclopropyl orbital. It is reported that this results in smaller pπ-orbital coefficients on each of the exo (0.54) compared to the endo alkene carbons (0.58).[16] Both of these effects result in a frontier orbital prediction that the endo alkene would be more reactive towards an electrophilic reagent such as dichlorocarbene, resulting in the reactivity shown above.
This approach is equal to the procedure introduced by Hehre, which involves superimposing the frontier orbitals onto an isovalued electron density surface.[17] When this is carried out, the endo alkene shows a much more sterically accessible π-orbital area than the exo alkene.
It is also interesting to evaluate the reactivity of 12 in terms of a transition state model. On inclusion of transition state entropy, enthalpy and solvation, there is predicted to be just a 0.1 kcal/mol specificity for the endo isomer.[18] In practise, as shown above, the endo isomer is produced exclusively, with no exo product (Cl and CCl2 on opposite sides of bridgehead carbon) being detected. This highlights the importance of many small effects in controlling regioselectivity and shows how stereoelectronic effects can dominate many aspects of alkene regioselection.
Mini Project
Enantioselective Synthesis of (+)-Estrone Exploiting a Hydrogen-Bond Promoted Diels-Alder Reaction
Starting from Dane’s diene and methylcyclopentenedione, (+)-estrone was very recently synthesised in a 24% yield.[19] The key step involves an enantioselective Diels-Alder reaction promoted by an amidinium catalyst. This paper represents a milestone achievement in enantioselective natural product synthesis. This mini project involves using a range of computational spectroscopic techniques to analyse compound 19 and 20, whilst comparing the data produced with recently reported spectral observations.
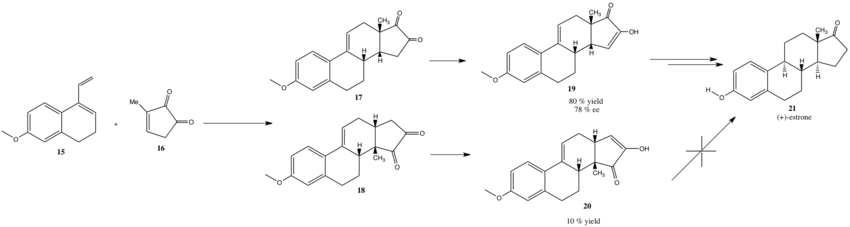
Estrone 21, due to its relatively simple structure and considerable pharmaceutical importance, has become a popular target compound for the development of novel synthetic methodologies.[20] This applies particularly to the Diels-Alder reaction: many breakthroughs in Organic Chemistry have been achieved by imparting constitutional and stereocontrol in reactions towards estrone and related estrogens.[21] This began with Dane’s successful synthesis of rac-17 from diene 15 and diketone 16, and developed into several other variants starting from diene 15 which were among the first applications of Lewis-Acid catalysed Diels-Alder reactions. A titanium based Lewis-Acid based catalyst enabled Dane’s earlier work to be improved by introducing high levels of constitutional control and enantioselection.
The first two reactions are kinetically controlled, the the catalyst ensuring endo attack of the diene as outlined below. Initial MM2 optimization yielding the data below and is consistent with 19 being the more stable product.
| Energy parameter | 19 energy (kcal mol-1) | 20 energy (kcal mol-1) |
|---|---|---|
| Stretch | 1.8869 | 2.1779 |
| Bend | 9.5386 | 15.1991 |
| Stretch-Bend | -1.5656 | 0.1677 |
| Torsion | -5.0440 | -3.4816 |
| Non-1,4 VDW | 17.8714 | -3.7640 |
| 1,4 VDW | 17.8714 | 19.0937 |
| Dipole/Dipole | -0.0831 | -0.1219 |
| Total energy | 22.7601 | 29.2709 |
Major Product.mol |
Compound 19 Gaussian Geometry Optimised
Minor Product |
Compound 20 Gaussian Geometry Optimised
Enantioselective catalysis was at first dominated by metal containing catalysts, but the past decade has seen an important number of highly selective reactions catalysed by hydrogen bond donors such as chrial ureas and thiroureas.[22] Acceleration of Diels-Alder reactions by hydrogen bonding was even reported prior to Lewis acid catalysis.[23] Yet hydrogen bond donors have until now been considered as relatively weak electrophiles, as Lewis acid based catalysis have been much more effective. This paper explains how a metal-free catalyst forming up to three bonds with diketone 15 promotes the Diels Alder reaction with diene 15 as efficiently as the best titanium TADDOLates used previously in this step, therefore leading to a new organocatalytic synthesis of (+)-estrone 21. The chiral amidine catalyst used during the Diels-Alder reaction is shown below.
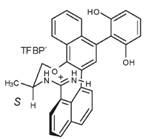
At first the synthesis of this large compound seems complex, however it was completed in moderate yield involving a 5-step synthesis.[24] A weakly coordinating counteranion (TFBP- = tetrakis(3,5-bis(trifluoro-methyl)phenyl)borate) was crucial to ensure effective binding of neutral substrates and also increases catalyst solubility in nonpolar solvents at low temperatures. The crystal structure of a similar catalyst reveals how hydrogen bond accepting host molecules may bind to the cationic cleft, as shown below.[25]
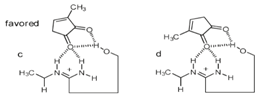
This schematic view of possible host-guest complexes formed when using compound 22 as catalyst shows the unfavourable orientation (d) due to OH---CH3 repulsion and the favourable orientation (c) leading to optimal guest activation, resulting in the 4:1 ratio of 19:20. The predominant configuration of 19 is explained by an endo attack of the diene 15 to the Re,Re face of the diketone 16 when bound to the chiral amidine.[26] The Curtin-Hammett principle is respected as stronger H-bonds will stabilize the diketone while increasing its reactivity. Yet it is also important to remember that other interactions in the transition state may be decisive in controlling the high enantioselectivity of this reaction. Catalyst 22 not only gives high enantioselectivity, it also increases the rate of reaction by a factor of 550 when compared to the uncatalysed reaction.
Discussion of 13C-NMR Spectra
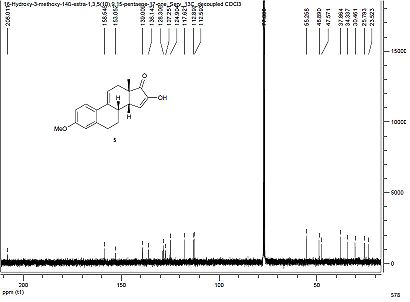
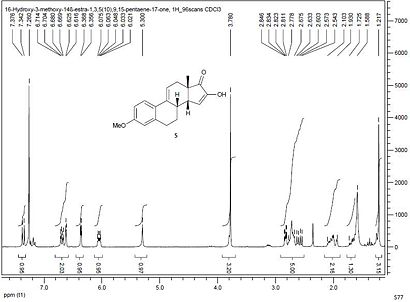
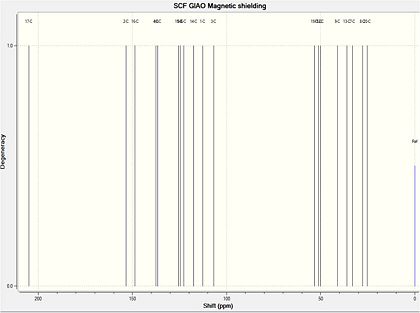
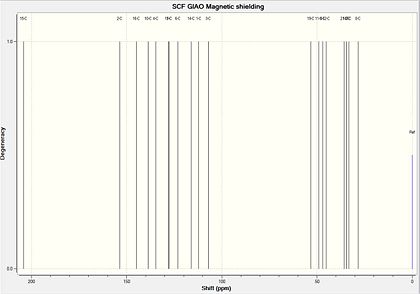
The 13C NMR spectra of both the major and minor product were predicted using the GIAO approach. Firstly, the geometry of the two compounds was initially oprtimised using the MM2 force field, and creating a Gaussian input file from the energy minimised structure. This was then submitted to be scanned using DFT=mpw1pw91, using a 6-31G(d,p) basis set, resulting in an optimised structure enabling NMR predictions to be made. The structures were again submitted to SCAN for NMR predictions, using chloroform as solvent as outlined in the literature. The literature 13C-NMR and 1H-NMR for compound 19 are shown below.
Literature Data For Compound 19
The GIAO approach is extremely sensitive to slight conformational changes. Although both compounds are reasonably rigid, being tetracyclic and having a C=C double bond in one of the rings, it is still likely that a slightly different conformation is adopted in both cases, compared to the Gaussian geometry produced, contributing to chemical shift deviations.
Compound 19: Computed 13C-NMR Spectrum
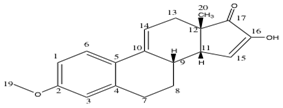
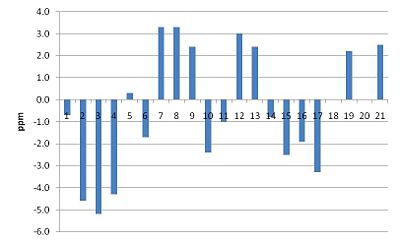
There is a good agreement between the computed 13C-NMR spectrum and the literature data, as the average deviation is 2.48ppm. However, there are four atoms for which there was a large deviation observed. Firstly, atom 3 was 5.7ppm below the literature value. This could have resulted from a slightly different conformation from reality, perhaps being derived from a hydrogen bonding like interaction between the hydrogen atom bonded to this carbon and the nearby strongly deshielded hydrogen atoms bonded to a carbon atom which is bonded to oxygen, deshielding this nucleus more than the computed value. Atom 16 was 4.6 less than the literature, which may result from poorly computed hydrogen bonding interactions with the solvent as this atom is bonded to an OH group. Nucleus 2 is also 4.9ppm less than the literature, this atom being bonded to oxygen. There may be some hydrogen bonding intermolecular interactions taking place at this oxygen atom that are not estimated effectively using this method. Yet an average deviation of 2.48ppm compares favourably with reported structural comparisons.
Compound 20: Computed 13C-NMR Spectrum
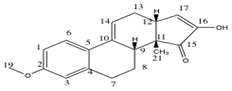
In this case the average deviation was slightly larger in magnitude, at 2.80ppm. There was only one carbon atom which disagreed by more than 5ppm, being number 3 which was 5.2ppm lower than the literature. This atom is in the same position as the nucleus in compound 19 which had the largest chemical shift deviation, therefore it is likely that the computational method is inaccurate at modelling the environment of this carbon atom. The electron withdrawing effect of the nearby oxygen atom may be underestimated, for example, or additional intermolecular forces or solvent interactions may cause this large deviation. But once again an average deviation of 2.80ppm is in agreement with recent compound identifications. To correct for a systematic error present for carbonyl carbons, the chemical shifts of these can be corrected using the following equation: δcorr = 0.96δcalc + 12.2. In each case this reduces the error observed by approximately 2ppm, increasing the accuracy of this method.
Key 13C-NMR Observations Enabling Product Identification
As the spectrum produced labels the number of each carbon atom causing a particular peak, compounds 19 and 20 can be identified using this computational method, which is more difficult using standard NMR spectroscopy. The key atoms involved in compound identification for both structures are atoms 15 and 17. In compound 19, atom 17 is doubly bonded to oxygen and is therefore is the most deshielded, having a chemical shift of 205ppm, whereas in compound 20 this atom is doubly bonded to carbon and has a chemical shift of 128ppm. Furthermore, in compound 20, atom 15 is doubly bonded to oxygen and is therefore is the most deshielded, having a chemical shift of 204ppm, whereas in compound 19 this labelled atom is doubly bonded to carbon and has a chemical shift of 125ppm. This highlights the value of computational methods to clearly indicate the different chemical environments of specific carbon atoms in each compound. Isotopic labelling of carbon atoms in this region of the diketone with 13C would also enable each compound to be more easily identified.
Computed 3JH-H Coupling Constant
When the optimized geometry of both compounds is fed into Janocchio the 3JH-H of the hydrogen atom shown for 19 below, can be calculated for both compounds.

In compound 19 3JH-H is calculated to be 4.03Hz, whereas in compound 20 there is only reduced coupling (1.11Hz) as now this hydrogen atom labeled above couples with the methyl hydrogens in this position. Both of these coupling constants are within 0.2Hz of the literature values, enabling identification of each compound to be completed. Additional comparisons were made with the literature and each computed coupling constant agreed to within 2Hz, but the characteristic coupling outlined above is most useful for identification purposes.
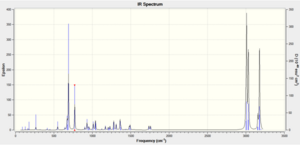
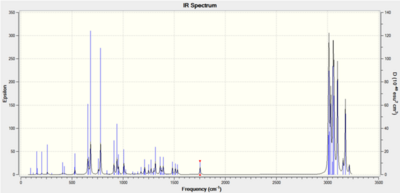
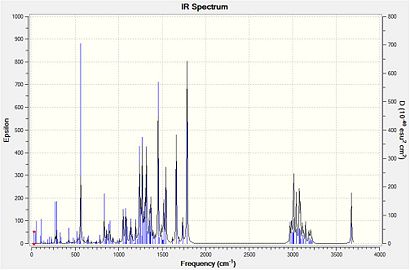
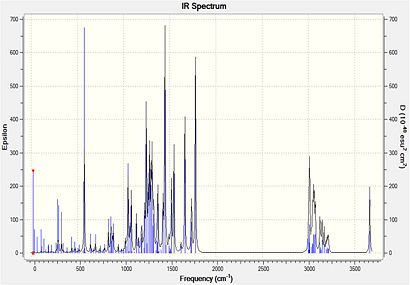
Computed Infrared Spectra for Major Product (Compound 19) and Minor Product (Compound 20)
Computed Infrared Spectra for Compound 19 (left) and compound 20 (right)
Infrared spectral data and inferences for compound 19
| Computed Frequency/cm-1 | Literature Frequency/cm-1 | Inference |
|---|---|---|
| 3673 | 3346 | O-H |
| 3121 | 3125 | =C-H asym |
| 3071 | 3076 | =C-H sym |
| 2924 | 2927 | aliphatic C-H |
| 1781 | 1785 | C=O |
| 1737 | 1735 | C=O |
| 1692 | 1690 | C=C |
| 1631 | 1627 | C=C |
| 1568 | 1570 | Enolate form C=O |
| 1452 | 1450 | Enolate form C=O |
| 1216 | 1212 | C-O |
| 1167 | 1163 | C-O |
Infrared spectral data and inferences for compound 20
| Computed Frequency/cm-1 | Literature Frequency/cm-1 | Inference |
|---|---|---|
| 3671 | 3341 | O-H |
| 3121 | 3127 | =C-H asym |
| 3079 | 3074 | =C-H sym |
| 2926 | 2930 | aliphatic C-H |
| 1779 | 1789 | C=O |
| 1732 | 1738 | C=O |
| 1691 | 1688 | C=C |
| 1633 | 1629 | C=C |
| 1563 | 1567 | Enolate form C=O |
| 1451 | 1447 | Enolate form C=O |
| 1165 | 1163 | C-O |
All of the key infrared absorptions expected in each compound have are observed in the computed spectrum. In general, each peak is within approximately 5cm-1 of the literature value. Upon further analysis of the output file, it was also learned that both the asymmetric and symmetric =C-H absortpions for each compound can be resolved using this technique as each absorption has a medium intensity. However, as this method produces the infrared spectrum of the compound in the gas phase, it does not account for the strong intermolecular hydrogen-bonding interactions which take place in when completing the spectrum using solid product on a KBr plate. For both compounds, the literature reports an absorption at approximately 3340cm-1 which is consistent with intermolecular hydrogen bonding occurring. But the spectra produced using Gaussian has an absorption at about 3670cm-1 which represents a free O-H bond. The characteristic absorption of a di-substituted aryl ring in the region (1700-1900cm-1) is not observed for either compound using this method. As both compounds have extremely similar bonds, certain identification of either compound using this spectroscopic method is extremely difficult, but it does provide a useful indication of the functional groups present in each product.
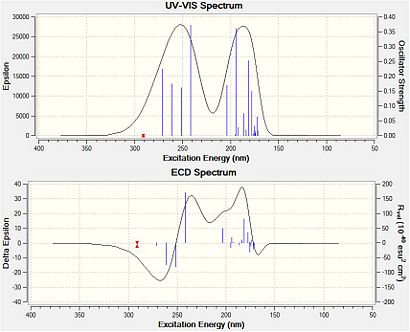
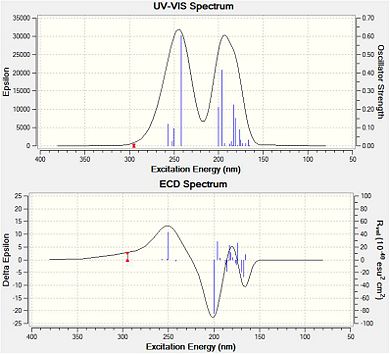
Interpretation of CD Spectra
UV-Vis and CD spectra for compound 19 (left) and compound 20 (right)
The time-dependent DFT method was used during this input, where the first 20 electronic singlet excitations are included.
The crucial difference between CD and OR is that the former is very much less sensitive to conformation, and hence the answer so much more definitive. Neither compound has any available literature optical rotation values or examples of CD spectra. Yet it is likely that with a greater source of information relating to both compounds their identification could be made from the spectra above. Initial calculations give an optical rotation value [ALPHA]D for compound 19 of +75(deg [dm g/cm3]-1) which compares favourably with a recently reported value of a similar derivative.[27]
Furthermore, an initial calculation for compound 20 gives [ALPHA]D = -19(deg [dm g/cm3]-1), agreeing with literature reported for compounds having similar conformations.[28]
Mini Project Conclusion
13C-NMR spectroscopy was useful in enabling the assignment of each carbon nucleus in both of the compounds analysed. For both products their spectra are almost identical, but important carbon environments can be understood and explained using this method. Infrared spectroscopy enabled a comparison with the literature data to be made and enabled the identification of the symmetric and asymmetric =C-H stretches which are difficult to observe in the laboratory. An input file to obtain the optical rotation of each compound was submitted but was deleted after running for 5 h.
Laboratory identification of 19 and 20 can be completed by 1H-NMR spectroscopy, although it is not imperative to do so due to the formation of almost exclusively 19 under kinetically controlled conditions.[29] When the reaction is carried out at -30°C in dichloromethane for two days using 15 mol % catalyst the resulting mixture contains almost exclusively cycloadducts 17 and 19, which were then isomerized by addition of acid. This gave a 91% yield of the ketoenols resulting from 19 and only traces of isomers resulting from 20 could be detected. Reduction of the enol triflates by published methods led to the enone shown below.
Chiral HPLC can be used to identify each of the enantiomers of this compound as 22 has a retention time of 12.4 min compared to 21.7 min for its enantiomer (DAICEL OJ, n‐hexane/PrOH 10 + 4, 0.8 mL∙min-1). A single recrystallisation of 22 from MeOH increases the ee from 81.0 % to 99.1 % ee, and three additional steps following known procedures give (+)-estrone.
During the infrared calculation the sum of electronic and thermal free energies was 7.66 kcalmol-1 lower for compound 19 compared to compound 20, which is larger than the approximately 2 kcalmol-1 stabilization achieved during the initial MM2 calculation. This indicates that there is a stronger thermodynamic driving force to form 19, but as the reaction is under kinetic control these energies are not extremely useful.
A 24% total yield of (+)-estrone can be achieved during this route, compared to 31% for commonly used titanium TADDOLate catalysed reactions, which also deliver much higher enantioselectivities of 93% ee. However the reaction rate recorded during amidine catalyst reactions compares favourably with those commonly reported using titanium TADDOLate catalysts which are easier to synthesise. On balance, there is currently a high level of interest in hydrogen bond donors to rival the most potent chiral Lewis acid catalysts, and this field is likely to become deeply investigated as the attractiveness of metal-free catalysts becomes extensively appreciated.
Conclusion
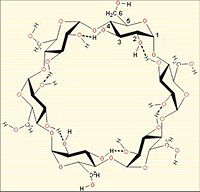
One example of the extending reach of computational chemistry towards organic applications is in the area of cyclodextrins (right). Cyclodextrins are a family of compounds made up of sugar molecules bound together in a ring (cyclic olgosaccharides).
These compounds are able to form host-guest complexes with hydrophobic molecules given the unique nature imparted by their structure. As a result, these molecules have found a number of uses in a wide range of fields such as pharmaceutical applications for drug release.[30]
Use of computational chemistry in this area has until recently been limited, due to the fact that they are relatively large, flexible molecules that are often studied experimentally in aqueous environments. This forces one to introduce many assumptions and restrictions so as to become unrealistic, creating a major hurdle for computational chemists. Many internal degrees of freedom exist for these molecules, making structural predictions both time consuming and difficult. Nevertheless, there have been a significant number of computational studies in the past decade that have led to a more profound understanding of the structure, dynamics and chemical behaviour of these compounds.
During the Mini-Project many of the advantages and disadvantages of computational methods were met. For example, after geometry optimization it was possible to predict the 13C-NMR spectrum for both compounds containing nineteen carbon atoms to within approximately 2.5ppm. However there were a couple of atoms which were consistently reported incorrectly using this method which were further analysed. A computation of the 3JH-H was made for a range of key nuclei, each of the values agreeing with reported data. Although the optical rotation calculation input was not returned, Electronic Circular Dichromism information enabled an estimate of the optical rotation values which were in agreement with similar compounds.
References
- ↑ Applications of Computational Chemistry to the Study of Cyclodextrins, K. B. Lipkowitz, 1998 DOI:10.1021/cr9700179
- ↑ Regio- and stereoselective control in the addition of Grignard reagents to the pyridine ring systemA. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
- ↑ Evaluation and prediction of the stability of bridgehead olefins; W.F. Maier, P.v.R. Schleyer., J. Am. Chem. Soc,, 1981,103DOI:10.1021/ja00398a003
- ↑ The Ultrafast Photoisomerizations of Rhodopsin and Bathorhodopsin Are Modulated by Bond Length Alternation and HOOP DrivenElectronic Effects DOI:10.1021/ja1056196
- ↑ Comparison of racemization processes in 1-arylpyrimidine-2-thione and 3-arylthiazoline-2-thione atropisomers and their oxygen analogs; C. Roussel, M. Adjimi and A. Chemlal, 1988, DOI:10.1021/jo00256a03 10.1021/jo00256a03
- ↑ Hyperstable Olefins: Further Calculational Explorations and Predictions; A. McEwen and P. Schleyer, 1985, DOI:10.1021/ja00274a016
- ↑ Evaluation and Prediction of the Stability of Bridgehead Olefins; W. Maier and P. Schleyer 1980, DOI:10.1021/ja00398a003 10.1021/ja00398a003
- ↑ Cage geometry controlled hyperstability in bridgehead olefins; Lalitha, 1990, DOI:10.1016/S0040-4039(00)97586-5 10.1016/S0040-4039(00)97586-5
- ↑ Steric Hindrance as a Mechanistic Probe for Olefin Reactivity: Variability of the Hydrogenic Canopy over the Isomeric Adamantylideneadamantane/Sesquihomoadamantene Pair (A Combined Experimental and Theoretical Study); R. Rathore, S. Lindemand and J. Kochi, 2002, DOI:10.1021/jo0200724 10.1021/jo0200724
- ↑ Hydrogenation of [7]paracyclophane: Formation of a hyperstable bridgehead olefin; Z. Li and M. Jones, 2001, DOI:10.1016/S0040-4039(01)80980-1 10.1016/S0040-4039(01)80980-1
- ↑ B. Halton and S. G. G. Russell, J. Org. Chem., 1991, 56, 5553-5556.DOI:10.1021/jo00019a015
- ↑ H.S. Rzepa, M. L. Webb, A. M. Z. Slawin and D. J. Williams, J. Chem. Soc., 1991, 765
- ↑ M.G. Banwell, N. K. Ireland, S. G. G. Russell and B. Halton, Aust. Org. Chem., 1991, 44, 555
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ S. D. Hahn and W. J. Hehre, J. Am. Chem., 1987,109, 663
- ↑ J.J.P. Stewart, J. Comput. Chem., 1989, 10, 209, 221.DOI:10.1021/jo00019a015
- ↑ Enantioselective Synthesis of (+)-Estrone Exploiting a Hydrogen Bond-Promoted Diels-Alder Reaction,2010,M. Weimar, G. Durner, J. Bats and M .W. Gobel, ', DOI:10.1021/jo100053j
- ↑ E. Dane and J. Schmitt, J. Liebigs Ann. Chem., 1938, 536, 196– 203 DOI:10.1021/jo100093j
- ↑ Highly Enantioselective [4 + 2] Cycloaddition Reactions Catalyzed by a Chiral N-Methyl-oxazaborolidinium Cation,Eda Canales and E. J. Corey, 2008, 10, 3271–3273 DOI:10.1021/ol8011502
- ↑ Small-Molecule H-Bond Donors in Asymmetric Catalysis,2007,A. Doyle and E. Jacobsen, DOI:10.1021/cr068373rj
- ↑ Axially Chiral Amidinium Ions with a Biaryl Skeleton: A New Class of Structure in Host–Guest Chemistry,2003,A. Gobel, DOI:10.1002/anie.199409841
- ↑ Enantioselective Synthesis of (+)-Estrone Exploiting a Hydrogen Bond-Promoted Diels-Alder Reaction,2010,M. Weimar, G. Durner, J. Bats and M .W. Gobel, ', DOI:10.1021/jo100053j
- ↑ Enantioselective Synthesis of (+)-Estrone Exploiting a Hydrogen Bond-Promoted Diels-Alder Reaction,2010,M. Weimar, G. Durner, J. Bats and M .W. Gobel, , DOI:10.1021/jo100053j
- ↑ Axially Chiral Amidinium Ions as Inducers of Enantioselectivity in Diels−Alder Reactions2000,T. Schuster, M. Bauch, G. Dürner and M .W. Gobel, ', DOI:10.1021/ol991276i
- ↑ Enantioselective Synthesis of (+)-Estrone Exploiting a Hydrogen Bond-Promoted Diels-Alder Reaction,2010,M. Weimar, G. Durner, J. Bats and M .W. Gobel, ', DOI:10.1021/jo100053j
- ↑ P. J. Stephens et al, Chirality, 2008, 20, 454-470. DOI:10.1002/chir.20466 DOI:10.1063/1.1477925 DOI:10.1063/1.1436466
- ↑ Enantioselective Synthesis of (+)-Estrone Exploiting a Hydrogen Bond-Promoted Diels-Alder Reaction,2010,M. Weimar, G. Durner, J. Bats and M .W. Gobel, ', DOI:10.1021/jo100053j
- ↑ K. Alder and G. Stein, Liebigs Ann. Chem., 1933, 504