Rep:Mod:bpw16yr2
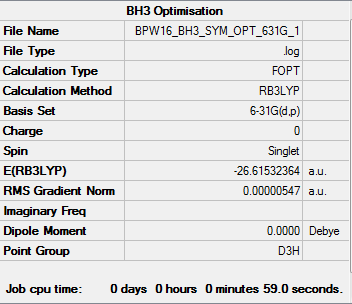
BH3 Molecule
Method - RB3LYP
Basis Set - 6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000043 0.001800 YES RMS Displacement 0.000028 0.001200 YES
Frequency .log file
File:BPW16 BH3 FREQ OPT 631G.LOG
Low Frequencies
Low frequencies --- -7.5936 -1.5614 -0.0055 0.6514 6.9319 7.1055 Low frequencies --- 1162.9677 1213.1634 1213.1661
Jmol Image
Optimised BH3 Molecule |
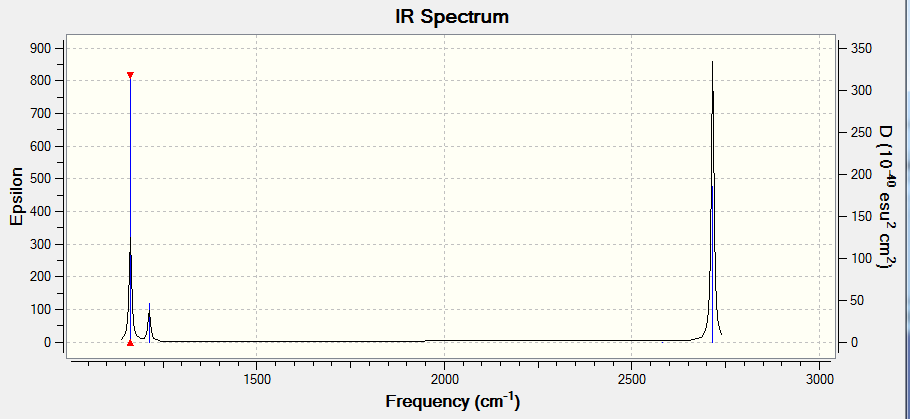
Vibrational Spectrum of BH3
| Wavenumber (cm-1) | Intensity (a.u) | Symmetry | IR Active? | Type |
|---|---|---|---|---|
| 1163 | 93 | A2 | Yes | Out of plane bend |
| 1213 | 14 | E' | Very slight | bend |
| 1213 | 14 | E' | Very slight | bend |
| 2582 | 0 | A1' | No | symmetric stretch |
| 2716 | 126 | E' | Yes | Asymmetric stretch |
| 2716 | 126 | E' | Yes | Asymmetric stretch |
There is 6 vibrations yet only three peaks in the IR spectrum. This is due to some of the vibrations being degenerate (having the same frequency, and hence energy, and so appearing at the same position in the spectrum). One of the vibrations (symmetric stretch) is also not IR-active (zero intensity) due to it not fulfilling the selection rule for IR (the vibration must cause a change in dipole moment).
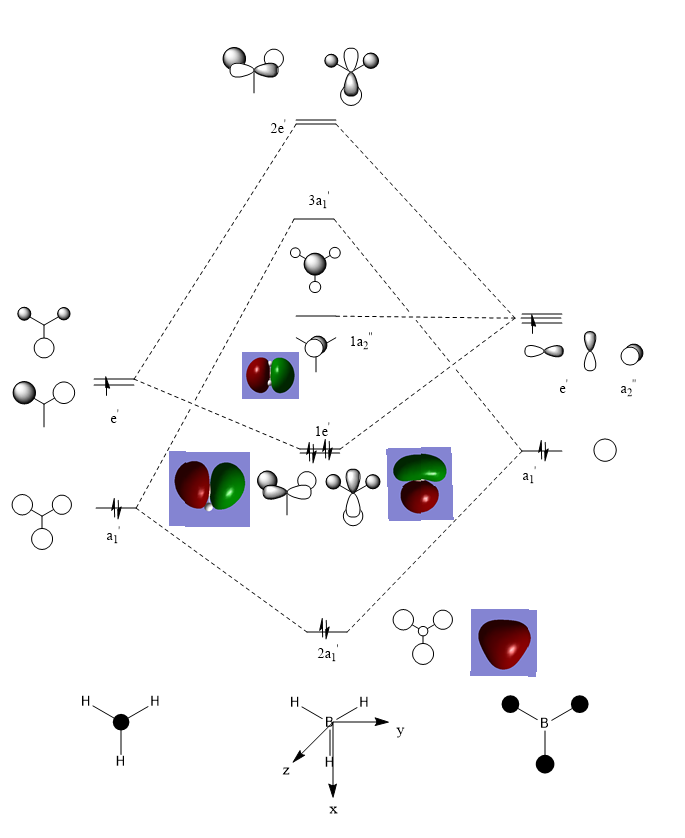
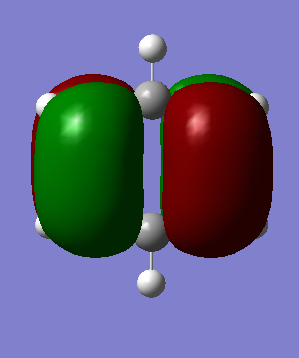
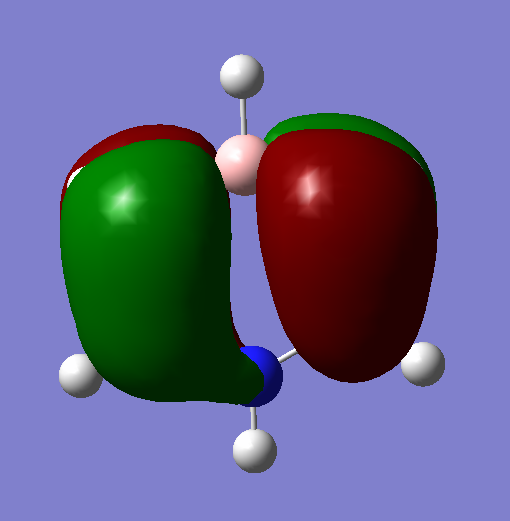
Valence MO Diagram of BH3
The LCAOs MOs are fairly similar to the computed MOs. The computed MOs show more overlap between the individual components, but this is because when LCAO MOs are drawn, overlaps are not drawn, just the individual components on top of each other. This shows that qualitative MO theory is of a good accuracy and can be used to usefully predict the shape and properties of MOs without complex calculations.
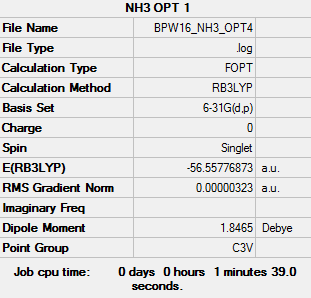
NH3 Molecule
Method - RB3LYP
Basis Set - 6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
log file
Low Frequencies
Low frequencies --- -0.0128 -0.0018 0.0010 7.1033 8.1047 8.1050 Low frequencies --- 1089.3834 1693.9368 1693.9368
Jmol Image
Optimised NH3 Molecule |
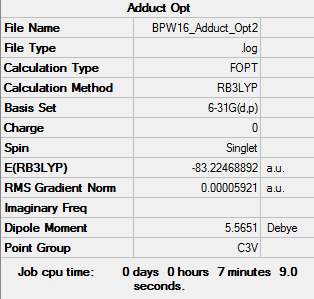
H3B-NH3 Adduct
Method - RB3LYP
Basis Set - 6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000121 0.000450 YES RMS Force 0.000057 0.000300 YES Maximum Displacement 0.000501 0.001800 YES RMS Displacement 0.000293 0.001200 YES
log file
Low Frequencies
Low frequencies --- -0.0012 -0.0008 -0.0004 16.6849 17.2568 37.3520 Low frequencies --- 265.9069 632.1985 639.3049
Jmol Image
Optimised Adduct H3B-NH3 Molecule |
Reaction Energy
E(NH3)= -56.55777 a.u.
E(BH3)= -26.61532 a.u.
E(NH3BH3)= -83.22469 a.u.
Hence, association energy of the dative bond:
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -0.05160 a.u. or -135 kJ/mol
This is a reasonable number to expect, as it is in the standard range for a bond strength (c.f. C-H bond strength = 338 kJ/mol).
Ng611 (talk) 22:42, 15 May 2018 (BST) Remember to cite your bond values (ideally from a textbook, databook, or paper)! What does this comparison say about the strength of the bond?
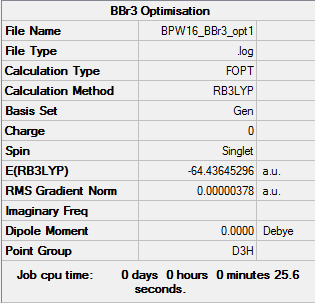
BBr3 Molecule
Method - RB3LYP
Basis Set - Gen (PP LANL2DZ used for Br atoms, 6-31G(d,p) used for B)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000035 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Frequency .log file
DSpace DOI
Low Frequencies
Low frequencies --- -0.0116 -0.0065 -0.0004 49.9506 49.9506 50.0315 Low frequencies --- 144.7605 144.7639 215.6181
Jmol Image
Optimised BBr3 Molecule |
Project Section - Investigating Aromaticity
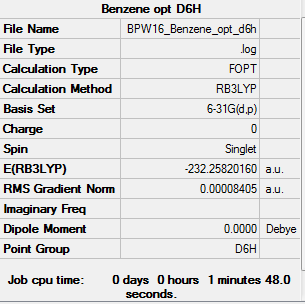
Benzene
Method - RB3LYP
Basis Set - 6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000194 0.000450 YES RMS Force 0.000077 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000289 0.001200 YES
log file
Low Frequencies
Low frequencies --- -2.1456 -2.1456 -0.0088 -0.0041 -0.0041 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Jmol Image
Optimised Benzene Molecule |
Borazine
Method - RB3LYP
Basis Set - 6-31G(d,p)
Summary Table
Item Table
Item Value Threshold Converged? Maximum Force 0.000083 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.000239 0.001800 YES RMS Displacement 0.000071 0.001200 YES
log file
Low Frequencies
Low frequencies --- -6.7766 -6.7766 -6.7465 -0.0210 -0.0104 -0.0104 Low frequencies --- 289.2507 289.2507 403.7827
Jmol Image
Optimised Borazine Molecule |
Charge Analysis
| Molecule | Charge (Colours) | Charge (NBO) |
|---|---|---|
| Benzene |  |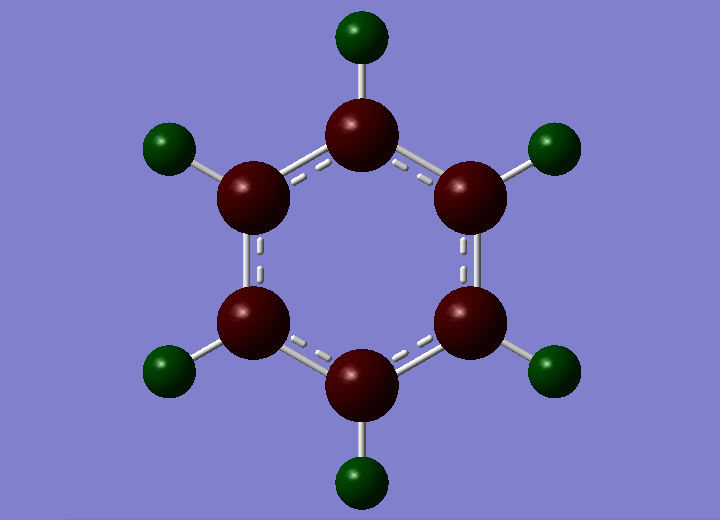
|
| Borazine |  |
|
| Atom | Charge (NBO) |
|---|---|
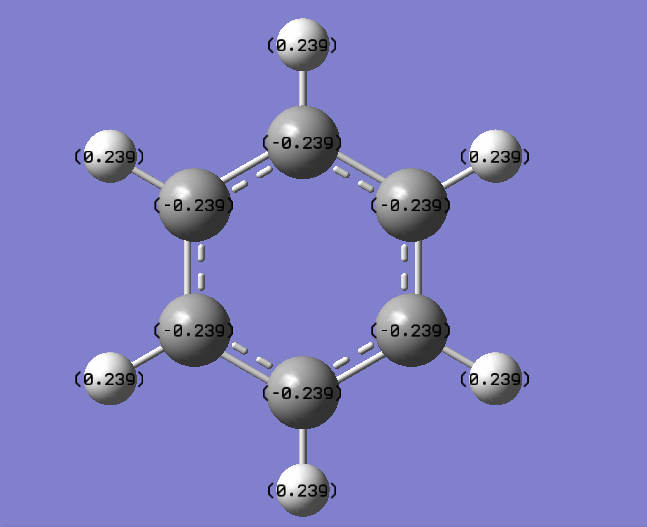
| C | -0.239 |
| H | 0.239 |
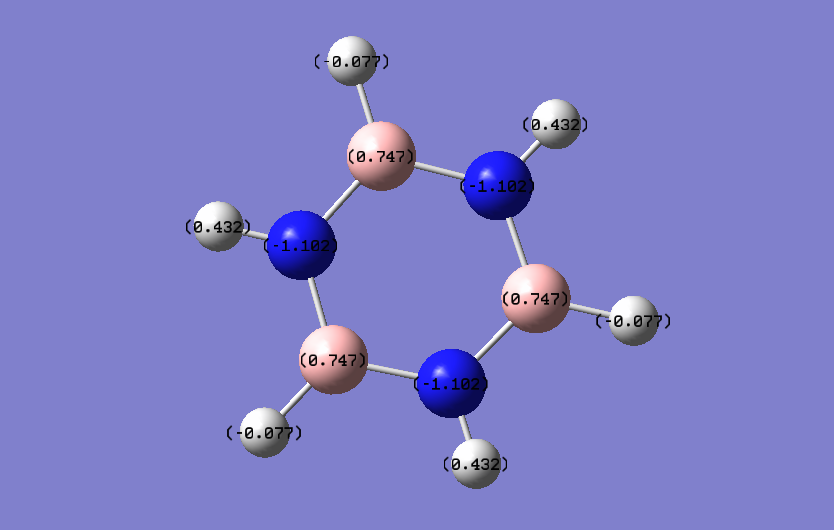
| Atom | Charge (NBO) |
|---|---|
| B | 0.747 |
| N | -1.102 |
| H (on N) | 0.432 |
| H (on B | -0.077 |
From the NBO charge analysis above, it can be seen that there is a greater charge distribution in borazine than in benzene. This is due to the electronegativity difference between the atoms. Carbon and hydrogen have electronegativities of 2.5 and 2.1 respectively, so there is not a great deal of polarity and hence the charge distribution is fairly small. The carbons have negative charge associated with them as they are more electronegative. This shows that the benzene ring will undergo electrophilic attack predominately.
The borazine molecule has a greater charge distribution with a large negative charge on the nitrogen, and a positive charge on the boron. The electronegativities of boron, nitrogen, and hydrogen are 2.0, 3.0 and 2.1 respectively. This shows that there is a fairy large electronegativity difference between the boron and nitrogen atoms, creating a polar bond. The nitrogens have a negative charge as they are more electronegative than the borons and hydrogens. The hydrogens have two different charges in borazine as they are bonded to two different types of atoms. The hydrogens bonded to borons are very slightly negative, as they are more electronegative than boron, with an electronegativity difference of 0.1. The hydrogens bonded to nitrogens have a positive, much larger charge, due to them being less electronegative than nitrogen, as well as having a greater electronegativity difference of 0.9. This shows that the nitrogen can act as a Lewis base, able to undergo electrophilic attack, while the boron can act as a Lewis acid, able to undergo nucleophilic attack.
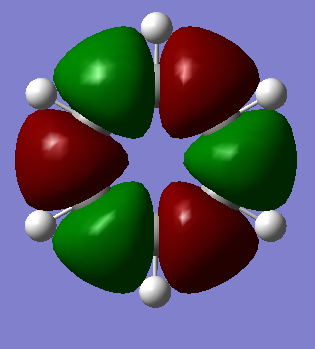
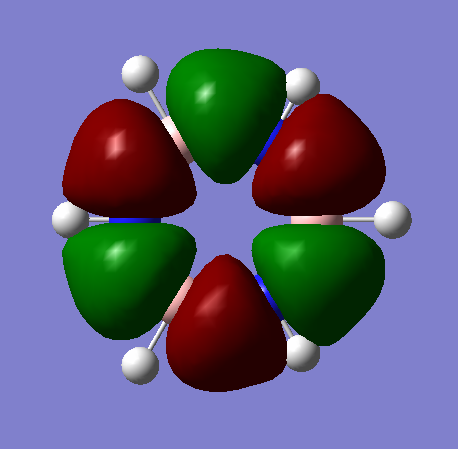
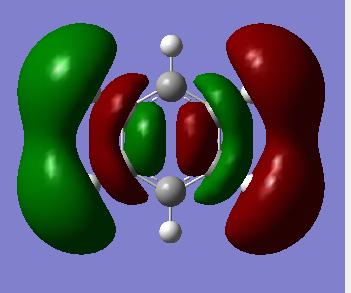
MO Analysis
| Benzene | Borazine | Comments |
|---|---|---|
 |
 |
These are MO numbers 14 and 15 for benzene and borazine respectively, showing that they have subtly different energies. They are both occupied, sigma MOs and this is the antibonding combination, with nodal planes through each ring atomic center and through-space, showing a C3 axis of symmetry, with no real difference in shape between the two different molecules. Some of the lobes for borazine are not the same shape as each other, simply due to the borazine molecule being less symmetric and the shape of the molecule being not a perfect hexagon unlike benzene, so slightly different orbital overlaps. The Nitrogen atoms are also more electronegative than the boron atoms and so electron density will be pulled and polarised towards them. It can be seen that there is a very slight difference between the two MOs, with the lobes being slightly more diffuse towards the nitrogen atoms rather than the boron atoms, with a slightly less symmetrical shape than in benzene. |
| Benzene | Borazine | Comments |
|---|---|---|
 |
 |
These are the MO number 20 for both molecules. It is an occupied, bonding pi MO overall with a C2 axis of symmetry, as there is through-bond p(z)-p(z) orbital overlap at each 'end' of the molecule, but through-space antibonding character, however this is weaker than the through-bond interaction as it is a closer, shorter-range interaction. There is a nodal plane, through-space, in between the two ends The shapes are largely similar for both orbitals, however there is slight distortion in the borazine MO, as the lobes where the p(z) orbtials have overlapped are not a symmetrical shape, as they are in the benzene MO. It can also be seen that electron density is being drawn towards the nitrogen atoms and away from the boron atoms, i.e. the electron clouds and hence the overlap and MO shape is polarised towards the nitrogens, as they are more electronegative than the boron atoms. |
| Benzene | Borazine | Comments |
|---|---|---|
 |
 |
These are the MO number 25 for both molecules. It is an unoccupied, overall antibonding orbital, with many nodal planes through atomic centers and through-space, with a mixture of pi and sigma components. The borazine MO has a quite different shape to the benzene MO. The benzene MO is much more symmetrical and less distorted. This is due to a number of reasons - firstly, the shape of the borazine molecule is less symmetrical than the benzene molecule, having different bond angles within the molecule. There are also polar BN bonds, due to the electronegativity difference, so it can be seen that electron density is polarised much more towards the nitrogen atoms, polarised quite strongly outside the nuclear region at the top of the molecule. It is clear that the borazine MO is less delocalised across the entire molecule, as the p(z) orbitals overlap less well due to an energy mismatch. |
Discussion of Aromaticity
Aromaticity was defined by Kekule after studying benzene. For a molecule to be aromatic, it must be a planar, ring molecule, which possesses a continuous, cyclic array of p-orbitals, that are orthogonal to the plane of the ring. In addition to this, it must obey Huckel's rule of aromaticity which states that for a molecule to be aromatic, it must contain 4n+2 p (or pi) electrons, where n is just an integer. Kekule defined aromaticity as hydrocarbons that are structurally similar to benzene, however, Erlenmeyer defined aromaticity as hydrocarbons that have similar properties to benzene, such as resonance stabilisation energies, ring currents, intermediate bond lengths between single and double bonds, and electrophilic aromatic substitution.
However, with modern computational methods, it can now be seen that aromaticity does not have to be associated with simply planar molecules, for example with polyacenes. It can be visualised that benzene in the crystaline state at 20K is not actually planar either, adopting a boat conformation because of sufficiently strong intramolecular forces. Aromaticity also does not have to apply solely to hydrocarbons, for example borazine is also aromatic, composed of B,N, and H. The aromatic stabilisation (resonance stabilisation) was originally considered to be from pi-electron delocalisation, however it is now postulated that the sigma-electron structure may also be a factor.
The MOs visualised with Gaussview vary in their similarity to those drawn through a LCAO method. While for highly symmetric systems such as benzene, with D6h symmetry, the pi orbitals are similar is shape to the LCAO ones, with the correct number of nodes, for less symmetric systems, or those containing main group elements other than C, the computed MOs can be different. For example, in borazine, due to the more polar, ionic BN bonds, there is considerable polarisation of the molecular orbitals towards the more electronegative nitrogen atoms and away from the boron atoms, distorting the shape of the MOs. There are also many sigma orbitals as well as the pi orbitals that are often focused on, all interleaved together. It also does not take into account subtle differences based on electronegativity or shape. For example, the borazine ring shape is not a perfect hexagon, with unequal bond angles, and with polar, more ionic bonds than in benzene. This means that the MOs computed are polarised much more towards the N atoms, as well as having slightly different overlaps. Just considering overlapping p(z) orbitals would not predict these subtly different sizes and shapes of the orbitals.
If a molecule is not planar, the p(z) orbitals, orthogonal to the plane of the ring (if it were planar) can not overlap as well and fully delocalise. However, as stated earlier, there are many molecules that are non-planar yet still posses the aromatic properties described earlier. This can also be seen in the borazine MOs, as they are clearly less delocalised than in benzene, due to the difference in symmetry, structure, and electronegativity. There may also be other orbitals involved such as sigma orbitals, which also contribute to the aromaticity, which are often ignored.
Application of AIM Parameters at Ring Critical Points for Estimation of p-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings.[1]
- ↑ DOI: 10.1002/chem.200700250 Chem. Eur. J. 2007, 13, 7996 – 8006.