Rep:Mod:bpw01201044
Introduction to Molecular Modelling 2 - Benjamin Woolley 01201044
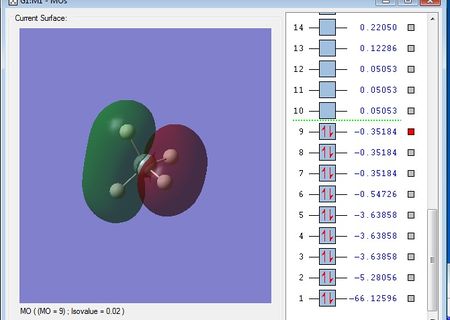
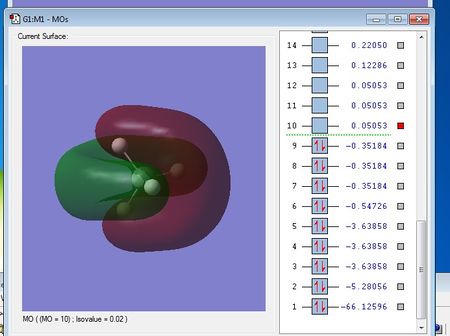
NH3 Molecule
Molecule name: Ammonia, NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (a.u): -56.55776873
RMS Gradient Norm (a.u): 0.00000485
Point group: C3v
N-H bond distance: 1.01798 A
H-N-H bond angle: 105.741 °
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986263D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
optimised ammonia molecule |
File:BWOOLLEY NH3 OPTF POP.LOG
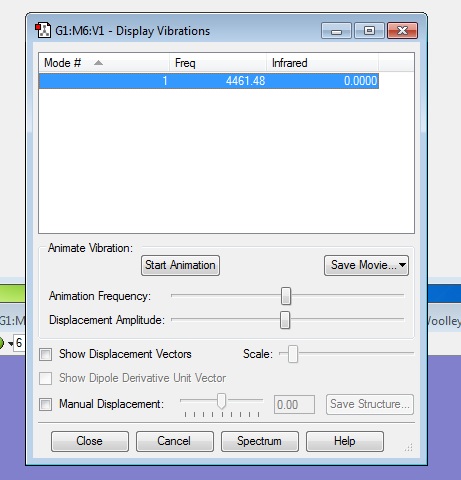
Using the 3N-6 rule, I would expect 12-6=6 vibrational modes, which is what I have found from the frequency analysis.
Modes 2-3, and 5-6 are degenerate.
Modes 1-3 are bending vibrations, modes 4-6 are stretching vibrations.
Mode 4 is highly symmetric
Mode 1 is known as the umbrella mode
In an experimental spectrum of gaseous ammonia, I would expect to see 4 bands due to there being 4 different frequencies of vibration present, all of which are IR active as they produce a change in dipole moment.
Charge on the N atom = -1.125
Charge on each H atom = 0.375
This agrees with what I'd expect as nitrogen is more electronegative than hydrogen and so a dipole will be created, with each hydrogen being delta positive and the nitrogen being delta negative, creating polar bonds.
N2 Molecule
Molecule name: Nitrogen, N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (a.u): -109.52412868
Point group: D*h
RMS Gradient (a.u): 0.00000365
N-N bond distance: 1.10550 A
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.248810D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
optimised nitrogen molecule |
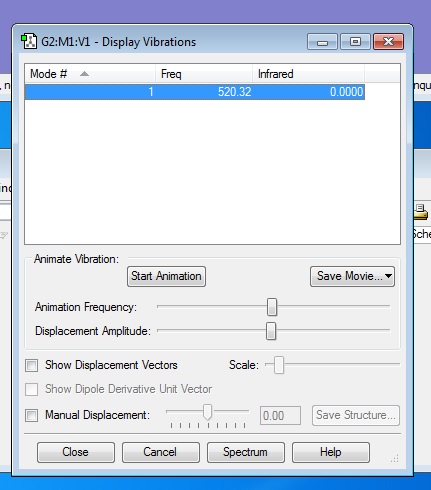
There are no negative frequencies.
Using the 3N-5 rule for linear molecules, I would expect there to be 6-5=1 vibrational mode, which is what I get from the frequency analysis.
The one vibrational mode is a bond stretching vibration and is not IR active because it does not produce a change in dipole moment. Therefore, in an experimental spectrum of Nitrogen there would be no bands.
Charge on each N atom = 0.000
This is in agreement with what I'd expect as N2 is a homo nuclear diatomic molecule, and so because it is formed from two identical nitrogen atoms, there is no difference in electronegativity, and hence no dipole.
H2 Molecule
Molecule name: Hydrogen, H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (a.u): -1.17853930
Point group: D*h
RMS Gradient (a.u): 0.00012170
H-H bond distance: 0.74309 A
Item Value Threshold Converged?
Maximum Force 0.000211 0.000450 YES
RMS Force 0.000211 0.000300 YES
Maximum Displacement 0.000278 0.001800 YES
RMS Displacement 0.000393 0.001200 YES
Predicted change in Energy=-5.852867D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7431 -DE/DX = -0.0002 !
--------------------------------------------------------------------------------
optimised hydrogen molecule |
There are no negative frequencies.
Using the 3N-5 rule for linear molecules, I would expect there to be 6-5=1 vibrational mode, which is what I get from the frequency analysis.
The one vibrational mode is a bond stretching vibration and is not IR active because it does not produce a change in dipole moment. Therefore, in an experimental spectrum of chlorine there would be no bands.
Charge on each H atom = 0.000
This is in agreement with what I'd expect as H2 is a homo nuclear diatomic molecule, and so because it is formed from two identical hydrogen atoms, there is no difference in electronegativity, and hence no dipole.
Analysis of Haber-Bosch process
N2 + 3 H2 → 2 NH3
E(NH3)= -56.55776873 au. This is the theoretical lowest energy structure for an ammonia molecule as calculated by Gaussian
2*E(NH3)= -113.11553750 au
E(N2)= -109.52412868 au. This is the theoretical lowest energy structure for a nitrogen molecule as calculated by Gaussian
E(H2)= -1.17853930 au. This is the theoretical lowest energy structure for an hydrogen molecule as calculated by Gaussian
3*E(H2)= -3.53561790 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579088 au = -146.478966598 kJ/mol. This is the enthalpy change of the reaction of nitrogen and hydrogen reacting to form gaseous ammonia. It is a theoretical value as all of the calculations have been carried out by Gaussian. Since this reaction produces 2 moles of ammonia, the calculated enthalpy change of formation for one mole of ammonia is therefore -73.239483299 kJ/mol.
Since it is an exothermic reaction, the ammonia product is more stable since it is lower in energy than the gaseous starting reactants.
Comparing this calculated value to a literature value, the literature value for the standard enthalpy of formation of ammonia is reported as -45.9 kJ/mol. [1] Therefore there is a difference of 27.3394833 kJ/mol between the theoretical value calculated in Gaussian and the experimental value reported in literature. The reasons for this could be that the experimental value is reported under standard conditions whereas the theoretical calculation has included certain assumptions and may have calculated the values under different conditions, for example temperature.
My Molecule: SiH4 Molecule
Molecule name: Silane, SiH4
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (a.u): -291.88802760
Point group: Td
RMS Gradient (a.u): 0.00000002
Si-H bond distance: 1.48485 A
H-Si-H angle: 109.47122 °
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-2.455460D-14
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4849 -DE/DX = 0.0 !
! R2 R(1,3) 1.4849 -DE/DX = 0.0 !
! R3 R(1,4) 1.4849 -DE/DX = 0.0 !
! R4 R(1,5) 1.4849 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
optimised silane molecule |
File:BWOOLLEY SIH4 OPTF POP.LOG
There are no negative frequencies.
Modes 1-5 are bending vibrations and modes 6-9 are stretching vibrations.
Using the 3N-6 rule, there should be 15-6=9 vibrational modes, which is in agreement with what I have found in the frequency analysis.
Modes 1-3, 4-5, and 7-9 are degenerate. Therefore, in an experimental spectrum I would expect to see 2 bands due there being 4 different vibrational frequencies, but only 2 that are IR active. Modes 4-5 and 6 are not IR active because they do not produce a change in dipole moment.
Charge on the Si atom = 0.629
Charge on each H atom = -0.157
This is expected as hydrogen is more electronegative than silicon and so there will be a dipole created between the Si and H atoms producing a polar bond.
| Molecular Orbital | Description |
|---|---|
 |
This is an occupied, non-bonding molecular orbital formed from the 1s atomic orbital on the silicon atom. It is non-bonding as the 1s orbital on Si is too low in energy to interact with the ligand group orbitals formed from the four 1s AOs from the hydrogens. It is very deep in energy and the overlap cannot be seen with the current isovalue and hence it does not contribute to the bonding. |
 |
This is an occupied, non bonding molecular orbital formed from a 2p AO on the silicon atom. It is non-bonding as the 2p orbital on Si is too low in energy to interact with the ligand group orbitals formed from the four 1s AOs from the hydrogens. It is much higher in energy than the previous MO discussed but it is still not in the HOMO/LUMO region, and hence does not contribute to the bonding. It can also be seen that there are three MOs that are degenerate due to there being three degenerate 2p AOs in Si, all of which form non-bonding MOs. |
 |
This is an occupied, bonding molecular orbital formed from the 3s AO from Si and one of the ligand group orbitals formed from the four 1s AOs from the hydrogens. It is relatively high in energy, but still not in the HOMO/LUMO region. Since it is formed from the valence orbitals from both silicon and hydrogen, it is a valence MO and it is very involved in the bonding. Also, the bonding overlap is extensive so all we see is one extended surface. |
 |
This is an occupied, bonding molecular orbital formed from 3 3p orbitals in Si and 3 ligand group orbitals formed from the four 1s AOs from the hydrogens. It is the HOMO for this molecule and so its energy lies in the HOMO region. Since all the atomic orbitals that contribute are valence orbitals, it contributes very strongly to the bonding in this molecule. It can also be seen that there are 3 degenerate MOs as there were three degenerate 3p AOs. |
 |
This is an unoccupied, antibonding molecular orbital formed from 3 3p orbitals in Si and 3 ligand group orbitals formed from the four 1s AOs from the hydrogens. It is the LUMO for this molecule and so its energy lies in the LUMO region. It does not contribute to the bonding of this molecule. It can also be seen that there are 3 degenerate MOs as there were three degenerate 3p AOs and 3 ligand group orbitals. |
Extra Calculation: Cl2 Molecule
Molecule name: Chlorine, Cl2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy (a.u): -920.34987886
Point group: D*h
RMS Gradient (a.u): 0.00002511
Cl-Cl bond distance: 2.04174 A
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000043 0.000300 YES
Maximum Displacement 0.000121 0.001800 YES
RMS Displacement 0.000172 0.001200 YES
Predicted change in Energy=-5.277239D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0417 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
optimised chlorine molecule |
File:BWOOLLEY CL2 OPTF POP.LOG
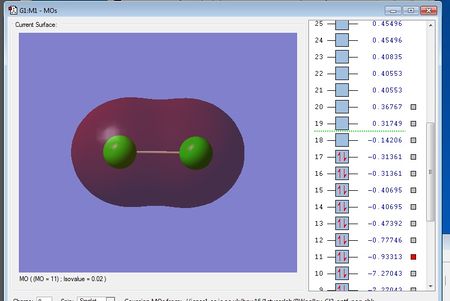
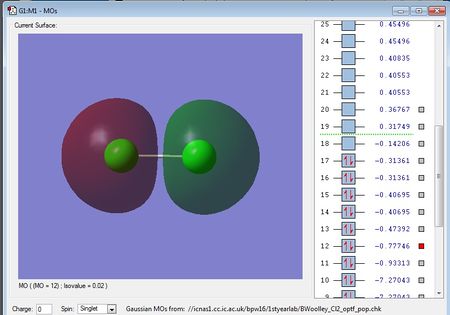
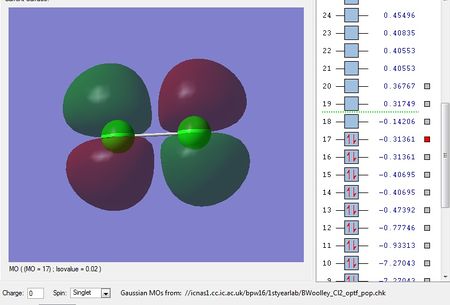
There are no negative frequencies.
Using the 3N-5 rule for linear molecules, I would expect there to be 6-5=1 vibrational mode, which is what I get from the frequency analysis.
The one vibrational mode is a bond stretching vibration and is not IR active because it does not produce a change in dipole moment. Therefore, in an experimental spectrum of chlorine there would be no bands.
Charge on each Cl atom = 0.000
This is in agreement with what I'd expect as Cl2 is a homo nuclear diatomic molecule, and so because it is formed from two identical chlorine atoms, there is no difference in electronegativity, and hence no dipole.
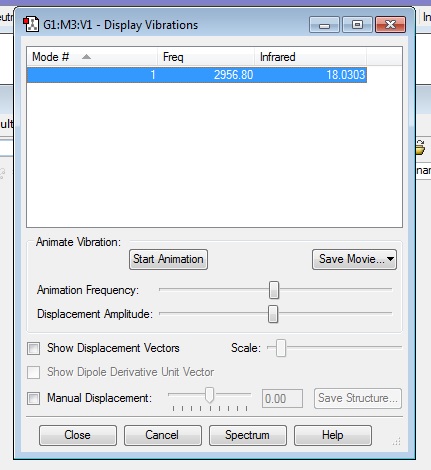
Comparing that to another linear molecule, I completed an extra calculation on an HCl molecule. I ran an optimization and frequency analysis as for all of the previous molecules above and obtained the following frequency analysis:
It can be seen that there is still only 1 vibrational mode, as to be expected from the 3N-5 rule, and it is still a stretching vibration but this vibration is IR active as there is a change in dipole moment for that vibration. This is due to there being a difference in electronegativity between hydrogen and chlorine, with chlorine being more electronegative than hydrogen, and so a dipole is created and it is a polar bond. Therefore, in an experimental spectrum of HCl, there would be one band observed.
Charge on the Cl atom = -0.284
Charge on the H atom = 0.284
| Molecular Orbital | Description |
|---|---|
 |
This is an occupied, 1σ bonding MO, formed from the core 1s AO on each chlorine respectively. It is very deep in energy and it is not possible to see the overlap with the current isovalue. It, therefore, does not contribute to the bonding very much. |
 |
This is an occupied, 4σ bonding MO, formed from the valence 3s AO on each chlorine respectively. These AOs overlap more strongly than the 1s AOs and so the bonding overlap is so extensive that all we see is one extended surface. The energy is much higher than the previous MO discussed too showing that it is a valence orbital and is very involved in the chemical bonding. |
 |
This is an occupied, 4σ antibonding MO, formed from the valence 3s AO on each chlorine respectively. It has a higher energy than the previous two MOs discussed and there is an appreciable energy difference between this antibonding orbital and the previous bonding orbital due to a better overlap of AOs. It is very involved in the chemical bonding. |
 |
This is an occupied, 2 pi antibonding MO, formed from a valence 3p AO on each chlorine respectively. It is the HOMO for this molecule and so its energy lies in the HOMO region. It can also be seen that there are two orbitals with the same energy (degenerate) due to there being 2 3p orbitals, orthogonal to each other that produce two pi star antibonding orbitals. These orbitals are very involved in the bonding. |
 |
This is an unoccupied, 5σ antibonding MO, formed from a valence 3s orbital on each chlorine respectively. It is the LUMO for this molecule and so its energy lies in the LUMO region. This MO does not contribute to the bonding of the molecule. |
References
- ↑ 1.H. Jia and E. Quadrelli, Chem. Soc. Rev., 2014, 43, 547-564.