Rep:Mod:boomerang0702

Cope Rearrangement: reactants

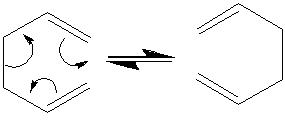
The cope rearrangement is an example of a 3,3-sigmatropic shift.In this section the reactants(and products) of the cope rearragement of 1,5-hexadiene were modeled using Gaussian.

Both anti and gauche conformers of 1,5-hexadiene were optimised at the HF/3-21G level of calculation and their symmetry and energy then calculated.

Gauche: Anti:

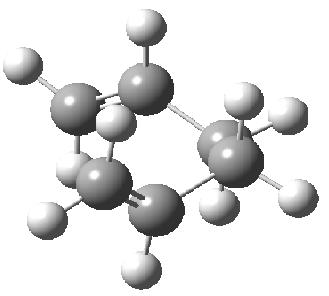
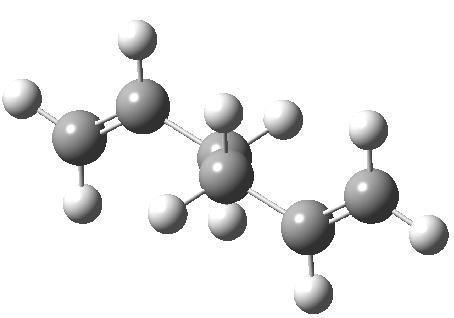
The gauche conformer has an energy of -231.69166699 hartree and C2 symmetry whereas the anti conformer has Ci symmetry and an enegy of -231.69253530 hartree. From this it was guessed that the lowest energy conformer would have anti symmtery and it was attempted to find this lowest energy conformer. The result is shown below with an energy of -231.69260235 hartree (lower than the previous two) and C2 symmetry.

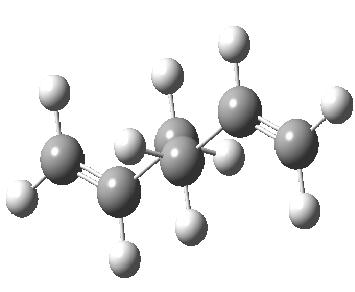
However, from the table found here Mod:phys3, it can be seen that the actual lowest energy conformer is gauche. This conformer was then built and optimised in gaussview(see below). It has an energy of -231.69266121 hartree, which is very close in energy to that of the predicted minimum, and C1 symmetry.

The Ci conformer was then optimised to the B3YLP/631G* level. The energy is now -234.61172184 hartree, higher than at the 321G level though the symmetry is still Ci. The geometry of the molecule has not changed much so this differance must be mostly down to the refinement of the calculation.

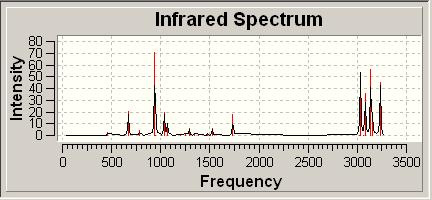
Finally vibrational analysis was carried out for the molecule at the same level of calculation, the IR spectrum is shown below. Key peaks include the C=C stretch at 1735, several CH stretchs about 3080-3200 and CH bends at 940 and 670cm^-1.

Several important energy terms were found in the thermochemistry section of the results file. From these it can be seen that the zero point energy is approximately 0.143 hartree ( 374kJ mol^-1

Sum of electronic and zero-point Energies=           -234.469182
 Sum of electronic and thermal Energies=              -234.461844
 Sum of electronic and thermal Enthalpies=            -234.460900
 Sum of electronic and thermal Free Energies=         -234.500730

Cope Rearrangement: Transition State

The cope rearrangement can proceed via either a chair or a boat transition state. In this section gaussian was used to explore the properties of both.

Chair Transition State

Firstly an allyl fragment was created and optimised at the HF/321G level. The bond lengths are 1.389Å and the C-C-C bond angle 124.2^o. This fragment was then used to form the chair transition state.

Two differant methods for transition state optimisation were used in this section. The first involved a simple optimisation and frequency calculation again at the HF/321G level.

Chair_TS

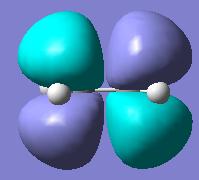
The interfragment distance is 2.021 slightly shorter than the starting distance of 2.2 and its energy is -231.619 hartree. Vibrational analysis of the transition state shows one imaginary vibration at -817.9 cm^-1 (see below). It can be seen that this corresponds to the Cope rearrangement as one of the interfragment bonds is breaking and the other is forming.

The second method involved freezing the coordinates of the breaking/forming C-C bonds and then optmising them seperately.

This gave a similar transition state also with an interfragment distance of 2.021 and an energy of -231.619 hartree. The imaginary vibration is now -817.8cm^-1 though still close to the previously calculated value and again shows one bond breaking and one forming.

Boat Transition State

The boat transition state was calculated using the QST2 method. In order for the calculation to work the central dihedral angle had to be set to 0^o and the internal C-C-C angles to 100^o. The resultant transition state is shown below.

Boat_TS

The interfragment distance is 2.140Å considerabley larger than in the chair transition state. This is most likely to accomodate for the steric clash of carbons 1 and 4. The energy is -231.603 hartree, 420 kj mol^-1 higher than the chair which is gain most likely due to steric repulsion. Calculation of the vibrational frequencies shows only one imaginary frequency (see below) at -839 cm^-1 It can be seen that one bond is breaking and one forming, as with the chair transition state.

IRC Method

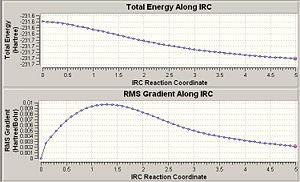
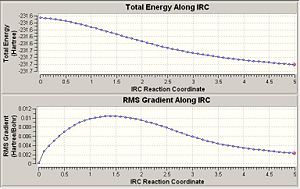
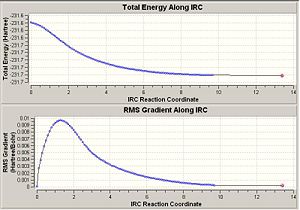
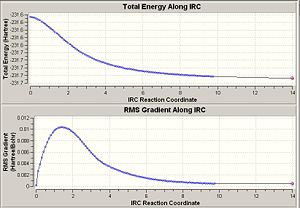
It has already been seen that there are many possible starting conformers for the rearrangement. In this section the IRC method was used to link the boat and chair transition state to the relevant conformer of the reactant/product. It was firstly used with 50 points giving the following results.

Chair TS:

Boat TS:

The plots show that the calculation has not reach a minimum in either case. There are three possible options i) optimse the structure to a minimum, ii) repeat the calculation with more points or iii) repeat the calculation, having force constants calculated at every step.

i)

Chair TS:

Boat TS

The energy for the IRC product of the chair transition state is -230.174 and has C2 symmetry. For the boat transituion state it is -231.683 and C1 symmetry. Neither of these corresponds to any of the reactant conformers shown here Mod:phys3. This shows that this method is not very useful and in fact it is known to be unreliable.

ii)

Chair TS:

Boat TS:

The chair transition state product shows C2 symmetry and has an energy of -231.692 hartree. It corresponds to the gauche 4 conformer. For the boat transition state the product has C1 symmetry and an energy of -231.684 hartree. It does not correspond to any of the given conformers as it is neither gauche nor anti but in fact periplanar.

iii) Unable to perform this as the calculation crashed in both cases.

Diels Alder Reaction

Reactants

All Diels-Alder reactions are in principle the cycloaddition of butadiene and ethene. In this section models of both butadiene and ethene were optimised using the AM1 method and the HOMO and LUMOs calculated, these afre shown belo along with their relative energies.

HOMO:, -0.357

LUMO:, -0.208

For butadiene the HOMO is assymetric with respect to the reflection plane and the LUMO is symetrical. . As the molecule contains a conjugate π bond system one might expect the C-C bond lengths to all be equal. However the C1-C2 and C3-C4 bond are 1.335Å whereas the C2-C3 bond length is 1.449Å. This indicates that the C1-C2/C3-C4 bonds possess more double bond nature than the C2-C3 which is primarily a singular bond. This can be seen clearly in the shape of the HOMO.

HOMO:, -0.395

LUMO:, -0.162

For ethene the HOMO is symetrical and the LUMO is assymetric with respect to the reflection plane. The C=C bond is 1.326Å long, which is shorter than any of the C-C bonds in butadiene due to its purely double bond nature.

Transition State

In this section the transition state was predicted using the frozen coordinate method. The optimisation was started from an “envelope” structure with an interfragment distance of 2Å. The results are given below.

The interfragment distance in the product is 2.209Å. The C1-C2 and C3-C4 bond lengths of the butadiene fragment are both 1.370Å whereas the C2-C3 is 1.394Å. For the ethene fragment the C-C bond length is 1.379Å. When compared to the bond lengths of the reactants it can be seen that the double bonds have become longer whilst the (mostly)single bond on butadiene has become shorter. This is to be expected as the product of the reaction possess only one C=C bond which would be in this position.

The vibrational frequencies were then calculated along with the HOMO and LUMO.

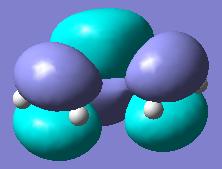
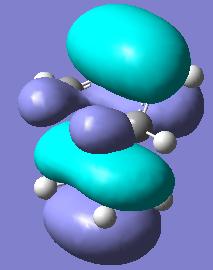
There is one imaginary vibration at -818cm^-1. This vibration shows that the formation of the two new C-C bonds occurs simultaneously which would be expected as pericyclic reactions (such as the Diels-Alder) occur concertedly. Below are the HOMO and LUMO of the transition state along with their relative energies. The HOMO can be seen to symmetric with respect to the plane of reflection and has a clear contribution from the HOMO of ethene. It is less clear which the butadiene MOs contributes but the LUMO seems to be a closer match which given that a HOMO-LUMO interaction between the two molecules is required would seem the correct choice.

HOMO: ,-0.300 LUMO: , 0.142

Regioselectivity

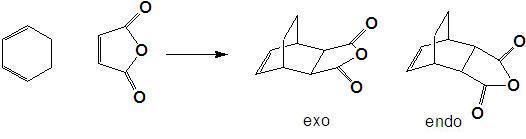
The diels alder reaction of maleic anhydride and cyclohexadiene can give two possible products, the exo and endo regioisomers. The endo isomer is predominates in accordance with Alder's endo rule. In this section the transition states of both isomers were calculated using optimisation at the HF/321G level.

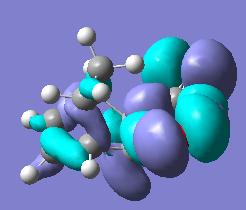
The exo transition state shown above has an energy of -605.703 hartree, C1 symmetry and an interfrgament distance of 1.547Å. Its HOMO is given below.

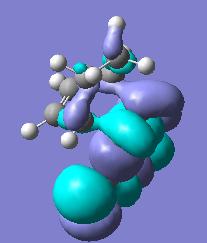
The endo transition state(below left) has an energy of -605.701 hartree, 26.25kJ mol^-1 higher in energy than the exo transition state, which is unexpected as the endo product predominates under kinetic conditions (i.e a lower energy transition state). This is most likely due to the limitations of running the calculation at such a low level. The fragment also has C1 symmetry and an interfragment distance of 1.560Å. Its HOMO is given below right.

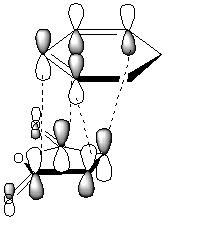
The prefferance for the endo product is believed to come from a mixture of steric and secondary orbital interactions. It can be seen above that the maleic anhydride fragment will undergo more steric repulsion with the sp³ carbons on the diene in the exo form which should in theory make it higher in energy.

Secondary orbital interactions(see below for example) between the diene and the maleic anhydride molecules would only be able to occur in the endo transition state as they would not be orriented towards each other in the exo form. These lower the energy of the transition state making the endo product more kinetically favourable.