Rep:Mod:bmmc1961
Module 3 - The Transition State
Reaction schemes were reproduced from the Lab Script page http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Module__3.2C_Experiment_3 Also it should be noted that latter parts of the experiment were preformed via the 'Chas' Remote Desktop Connection, at Imperial College. However initally vibrational and MO analysis could not be preformed or studied. After a personal consultation and investigation with Prof. Rzepa, this was altered and allowed the full experimental procedure to be done away from the College Campus.
The Cope Rearrangement
Optimising the Reactant and Products
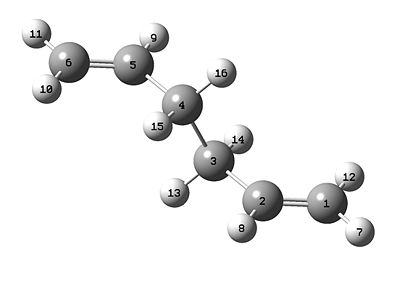
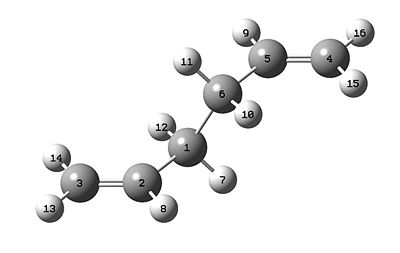
The molecule of 1,5-hexadiene was drawn, with an anti linkage for the central four carbon atoms. The structure was optimised using the Hartree-Fock method and the 3-21G basis set. The optimised structure is shown below, along with the summary which displays the energy as -231.67756834 hartrees.
The symmetry was found to be C1, relating to the lack of symmetry from this particular anti conformer.
The molecule was redrawn however this time with a gauche linkage for the four central atoms. Again the structure was optimised using the using the Hartree-Fock method and the 3-21G basis set. It was expected that the gauche conformation would be higher in energy than the anti as the torsion angle between the two substituent carbon chains is 60˚, much closer than the anti arrangement, and therefore increased steric interaction would result. The optimised structure is shown below, along with the summary which displays the energy as -231.68916020 hartrees. This is lower than the previous ani conformer, and which correlates with the previous prediction.
The symmetry was found to be C1, relating to the lack of symmetry from this particular gauche conformer.
It is suspected that the lowest energy conformation would be the anti conformation, as this arrangement seems to have the most conformers wherein the alkene groups are furthest away. Both structures above are tabulated in Appendix 1. The gauche conformer above relates to the gauche6 conformer in Appendix 1, and there is perfect accuracy. However the anti conformer above, which relates to anti4, does show deviation from the energy value in the appendix, by 0.0134 hartree.
The anti2 conformer was also drawn and optimised, as below.
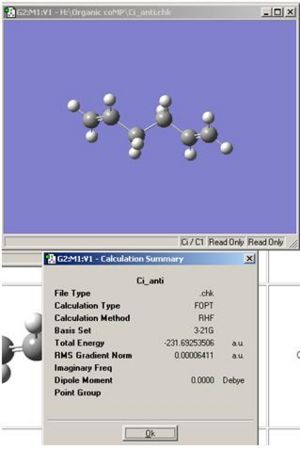
As can be seen the energy is accurate in terms of the tomic unit hartree, with Appendix 1 when rounded to 5 decimal places. It is also accurate in terms of symmetry as the optimised molecule above also has a centre of inversion, i, hence the Ci point group.
The above conformer was then re-optimised with the more advanced method, DFT, and the higher basis set, B3LYP/6-31G*. As expected the higher basis set, re-optimises the structure to a more energetically relaxed level. However unlike the small variations between the above structures and the respective analogues in Appendix 1, this time when a more advanced method/basis set is applied the variation in energy is quite substantial.
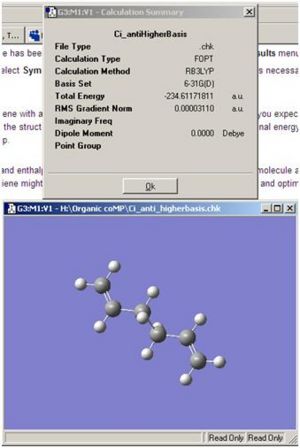
| Basis Set | Energy (hartree) | |
|---|---|---|
| 3-21G | -231.69253506 | |
| B3LYP/6-31G* | -234.61171811 |
As tabulated above there is almost a 3 hartree variation in stabilised energy, when the more advanced basis set is used. This tells us that the more advanced basis set should always be used, where applicable, when comparing energy's of structures from different sets, or when thermodynamic/kinetic properties are to be accurately calculated as these properties relate to the relaxed energy of a molecule that is found from optimisations.
Geometric variations could also be observed when the higher basis set was used for optimisations.

The C=C bond distance for the 3-21G basis set was 1.31627A whereas the same distance was 1.33349A under the B3LYP set. This perhaps relates to the idea that the earlier basis set does not accurately follow the first derivative of the PES, in that although it is near an energy minimum the limitation of the method settles for any point within a respectable range of the minimum; meaning that the optimised structure is at very close to a energetic and geometric minimum but notquite on thevery specific point. The more advanced set, does not have such a great minimum and so optimises even closer to the energetic and geometric minimum, i.e where the second derivative is postive.
Further geometric variations can be seen below in terms of:
1)C=C-C torsion angle
2)C=C-(C)-H torsion angle

Both of which are as a result of the discrepincy in C=C bond distance.
Frequencies and thermochemical properties
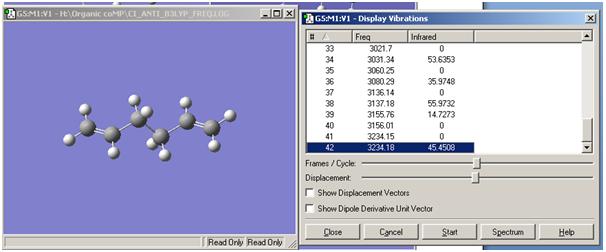
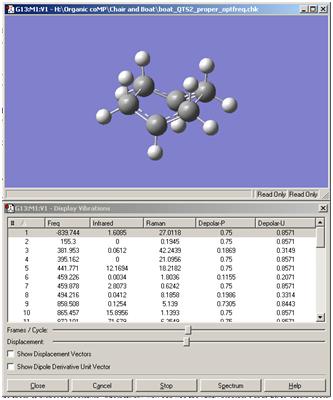
A frequency calculation was also performed on the 1,5-hexadiene anti2 conformer and is shown below:
There are no imaginary frequencies which relate to a transition state; some have an intensity of zero but this relates to no change in symmetry or diploe moment and therefore results in an IR inactive vibration.
By analysing the .log file, thermodynamic properties can be extrapolated. Of particular use are the properties below (in hartrees):
Sum of electronic and zero-point Energies= -234.469183
Sum of electronic and thermal Energies= -234.461841
Sum of electronic and thermal Enthalpies= -234.460897
Sum of electronic and thermal Free Energies= -234.500747
This exercise allows the computational chemist to understand the different conformations of molecular structures, and importantly, how each conformer has a separate stable energy, which as a result has a profound eaffect upon thermodynamics, reaction kinetics, and reactivity. Furthermore computational chemistry can allow insight into near experimental values of such properties.
Optimizing the "Chair" and "Boat" Transition Structures
Chair Transition State Optimisation
As both the boat and chair transition states contain two C3H5 allyl fragments, both fragments were optimised separately and incorporated into one window, then two different techniques were employed to optimise the overall chair transition state. The first technique involved approximating inter fragment distance and from here estimating the Hessian, or force constant matrix. The optimisation was performed to a transition state (TS(Berny)) as we are attempting to find the energy maximum on the PES which correlates to transition state, and under the Hartree-Fock method and 3-21G basis set. Transition state molecular dynamics tells that a frequency or forbidden vibration should occur at a negative which relates to the vibration between the two transition fragments. As a result, 'Opt=NoEigen' was included in the calculation as it relates to no eigenvalue, which prevents the calculation from ceasing if more than one imaginary or 'forbidden' frequency is found.
Initially, when the optimisation was run, it ceased with no final structure; 'Error termination request processed by link 9999.'This perhaps relates to the number of maximum optimisation cycles, which has been exceeded in the calculation or the calculated force constants and energies of each step of the optimisation are oscillating whic prevents a final, definitive stucture being calculated. When the calculation was sent to scan, the returned geometry had a inter fragment distance of 2.5, which is more than the original estimate.
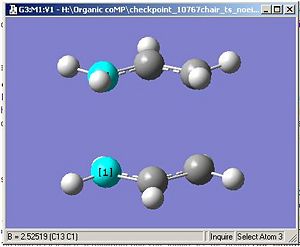
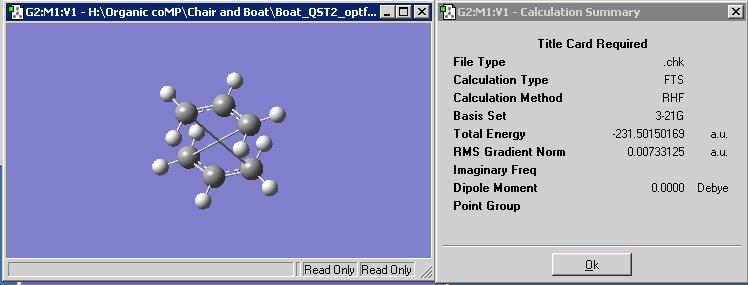
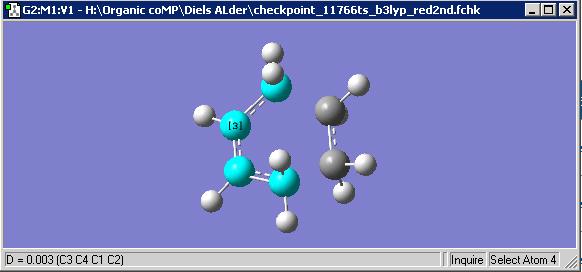
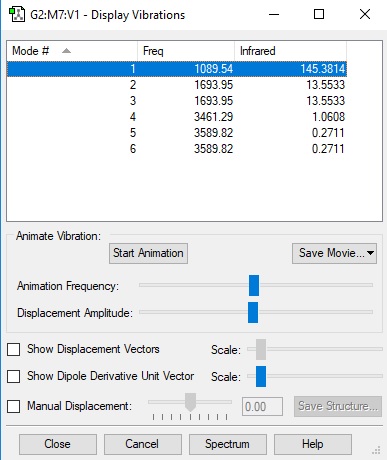
However, eventually, after increasing the number of optimisation cycles (maxcycle=N) the correct optimisation was gained as shown. The frequencies were also calculated and given that there is an imaginary vibration in line with the literature value (-817.1cm-1), it is a fair estimate of the chair transition state given the basis set level.
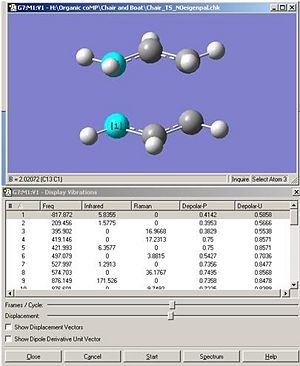
The inter-fragment distance is optimised to 2.02A. As shown below the stable energy is -231.61932244 hartree.
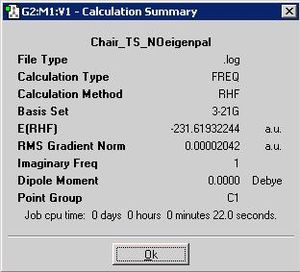
A second technique was also employed to optimise the chair structure, namely the frozen co-ordinate method. This entailed initially freezing the forming bonds between the two allyl fragments to 2.2A, and running an minimum optimisation on the rest of the structure. From here, which should be similar to the structure found from the previous 'no-eigen' T.S. optimisation, the frozen bonds are further optimised based upon T.S. Unlike the 'no-eigen' method, the force constant is never calculated, instead the Hessian is estimated and includes the approximate of the inter-fragment distances i.e. the information from the first part of the optimisation. This added information, which is approximated within a structure which is otherwise optimised, allows the co-ordinates to become even more accurately described once the co-ordinates have been differentiated along.
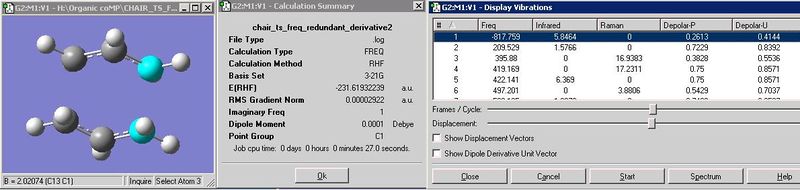
Both transition state optimisation techniques were performed under the Hartree Fock/3-21G method. There are no major differences in the transition state strucutres and properties that are supplied. They both contain imaginary (negative) frequencies which is consistent with the transition state, as these frequencies occur between the the co-ordinates that are have a bond formed/broken between them in the final structure. Both have distance between these co-ordinates of 2.02A to 3 s.f and only have a difference of 0.00002A. The 'redunant' technique had the higher energy transition state but only by 0.00000005 hartree. Perhpas this tells that this is the more accurate as the transition state relates to an energy maximum. There is a slighlty significant variation in the RMS Gradient Norm in that the redundant technique is 0.0000088 hartree. This relates to the gradient of particular point of the structure along the RMS. It is unclear whether this is the gradient of the tangent or the normal (as it states 'norm' in the title) but if it does relate to the normal, then this could mean that the redundant technique is more accurate as it has a higher normal gradient, which correlates to a perpendicular tangent gradient closer to zero, and therefore closer to the absolute maximum on the RMS (where gradient=0) relating to the transitions state. Of course if the 'RMS Gradient Norm' relates to simply the tangent gradient then the no-eigen technique is marginally more accurate as it has a gradient closer to zero.
It is noted that at a higher basis set these almost indistinguishable subtleties would become more accentuated due to an increase in accuracy and complexity in terms of methodology.
Boat Transition State Optimisation
The boat transition state was also optimised via a third technique; the QST2 technique. This works by drawing out the reactant and product of the rearrangement and allowing the technique to interpolate between the two structures to give the most suitable transition state between the two. However great care must be taken in numbering the product in such a way that it correlates to the rearrangement of the reactant i.e. that the bonds broken in the product is numbered in the same way as the bond that is existing in the reactant.
Initially the molecules were orientated and numbered in the following fashion and a TS(QST2) optimisation was run .
However the optimised structure failed to give a legititmate structure in that the bond formations were to the opposite atoms on the fragment.
Essentially there was a failure to identify a possible rotation around the central atoms of the two fragments. Typically, under such orientations of the reactant and product, the transition state can never be successfully optimised. Therefore, in order to gain a legitimate, albeit not necessarily a purely accurate, transition state one must in effect alter the reactant and product closer to the suspected structure. This was done by altering the central dihedral angle to 0 degrees and both of the C-C-C angles for the same four central carbons to 100 degrees. This was done for the reactant and the product, so both were closer to a rough estimate of the boat T.S. and the range of possibilites for the T.S. were significantly reduced.
As can be seen this is a legitimate boat T.S. as there is an imaginary frequency. Also the correct bonds are formed for the product. However in this conformation the inter-fragment distance between the newly-formed bonds is 2.14A. This is either as a result of the boat conformation as compared to the chair as both fragments are in the same orientation and so there are increased repulsive forces, or as a result of the the TS(QST2) optimisation technique.
From here, by analysing both the calculated chair and boat transition states, one can make a crude approximation of which transition state leads to which conformer. From the previous calculations one can state that the chair T.S. leads to the gauche conformation and the boat T.S. leads to the anti conformation. However to allow for a definitive investigation, an IRC was run with calculation of the force constant only at the start of the process, the resepective T.S. not as the calculation input, and only allowing calculation in the forward direction of the reaction co-ordinate.

As can be seen, the T.S. hasnt quite converged to a minimum geometry yet. Therefore one of three properties can be altered. It was decided to calculate the force constant at every of the 50 steps so as to gain a closer approximate instead of relying on the force constant calculated at the beginning of the calculation.
The final structure from the IRC was gained below:
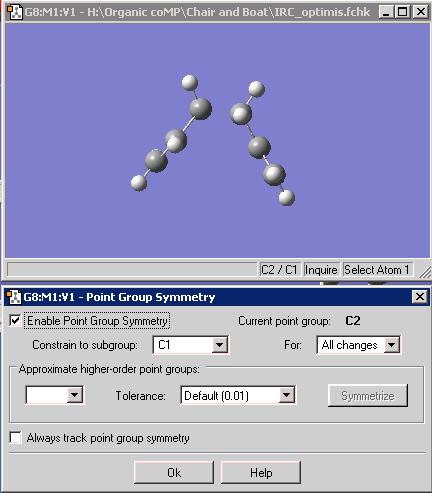
From the final geometry, a further optimisation was preformed to attain an optimised structure of the reactant, or as the reaction is a rearrangement, the product. This is because the IRC did not produce a structure that was a minimum, as shown by the graph below.
The optimised structure has a respectable C-C distance of 1.55A, and when the point group is probed, it demonstrates a C2 point group. Therefore we can say that the chair transition state comes from the reactant that is in the gauche conformation with C2 symmetry. Conversely the boat structure comes from a gauche conformation with C1 symmetry, with a higher energy to the 'C2' conformer and this reflects the fact that this conformation is energetically the lowest of the gauche conformers and the chair transition state is the lower in energy than the boat. This correlates with the fact that in both cases the conformation of the reactant goes to the transition state nearer in energy.
Calculation of Activation Energies
Calculated at 0K, the Activation energies were calculated at the B3LYP level of theory. The total energy of the reactant was found and a frequency calculation on the optimised TS was performed to find it's total energy. The energy difference related to the energy of activation for the whole re-arrangement as the energy of the TS represented the maximum point on the PES. All values were gained from calculations performed at the far more accurate B3LYP level of theory
Chair TS Conformation
Reactant: Sum of electronic and zero-point Energies= -234.469183 hartree
Transition State: Sum of electronic and zero-point Energies= -234.418991 hartree
Therefore activation energy= 31.49 kcal/mol This is just outside the error range of the expermental value, yet it well within the accepted estimate range.
Boat TS Conformation
Reactant: Sum of electronic and zero-point Energies= -234.469183 hartree
Transition State: Sum of electronic and zero-point Energies= -234.402344 hartree
Therefore activation energy= 41.94 kcal/mol This is within error range of the expermental value via the boat transition structure.
It was attempted to calculate the energies at 298.15K using the method of altering temperature for calculations in the previous exercise and the Freqchk method. However errors were encountered for both methods and due to time constraints, this added calculation was not attained.
This exercise enabled one to understand the techniques involved in attaining transition states and therefore following the route the possible conformers involved in a reaction. This will play a key role in understanding the orbital interactions and preferred arrangements of products in classical reactions such as the Diels Alder reaction below.
Diels Alder Reaction
The Diels Alder reaction is an example of a pericyclic reaction, more specifically a cycloaddition. In it two σ bonds are formed via interactions between the HOMO/LUMO of a dienophile and a diene, more specifically the π/π* orbitals. These interactions deal with a transfer of electrons from one orbital to another on a neighbouring molecule. This results in the formation of a new bond being formed, σ or π, dependant upon the new destination of the electrons. However when there is a transfer of electrons between two MO's symmetry observed in that the two orbitals in question must both be symmetric or anti-symmetric with respect to the plane. There are also favourable secondary orbital interactions which do not deal with the definite transfer of electrons from one orbital to another, rather a electrostatic interaction between an occupied and unoccupied orbital; this enhances the kinetic stability of one orientation over another. This can be usurped though via steric hinderance between two fragments or even destabilising interactions between the opposite to before, but between two occupied orbitals.
Cis-butadiene
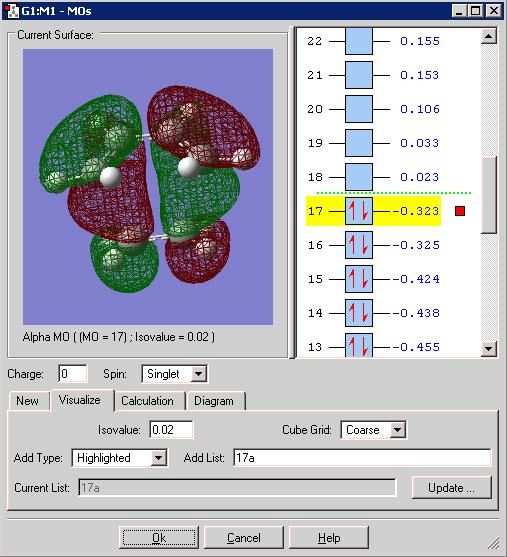
Cis-butadiene was optimised frist via semi-empirical calculation then via the Hartee-Fock method and finally B3LYP. The HOMO below is from the Hartree Fock method:
It can be seen that the HOMO is anti-symmetric with respect to the plane slicing vertically through the central two carbons.
The LUMO below was found via the Hartree-Fock method:
It can be seen that the LUMO is symmetric with respect to the plane slicing vertically through the central two carbons.
Cis-butadiene + Ethylene Transition State
The transition state was formed via the 'redundant' method i.e. the new σ bonds were frozen at approx 2.2A while the rest of the molecule was optimised, then from here the new σ bonds were unfrozen and the structure was optimised to a TS (Berny), never calculating force constant, but following the derivative via a guess Hessian. All calculations were perfromed firsrt under a semi-empirical method but all results below are from the B3LYP method.
The average C-C bond length containing two sp3 hybridised carbons is 154ppm 1. The average bond length for two sp2 hybridised carbons is 135ppm
The forming sp3 σ bond lengths (between the fragments) = 156ppm
This bond is in the region of the length quoted for a bond containing two sp3 hybridised carbons. Therefore we can speculate that the new bond will also be of this regime. It is slightly longer however as this is only a transition state and the bond is not fully formed. The van der Waals atomic radius for a carbon atom is approx 170ppm2, this tells us that as the partly formed C-C bond is shorter than this, that there is a definite interaction between the two atoms as they could not be as close otherwise.
The other sp3 σ bond lengths (as highlighted) = 151ppm
This σ bond value is shorter than the previous one because one of the carbons is sp2 hybridised and therefore the electrons have stronger forces imposed upon them by this carbon, reducing the bond length.
The other forming sp2 π bond lengths = 134ppm
The frequency analysis reveals an imaginary vibration which certifies the fact that it is a transition state. The vibration shown below has the simultaneous and symmetric movement of both of the carbons of both of the new sigma bonds towards each other. It can be therefore said that the two new bonds are formed in a synchronous fashion
This compared to the lowest positive frequency, which is simply asymmetric twisting of both fragments.
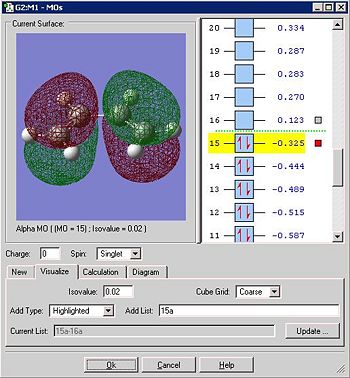
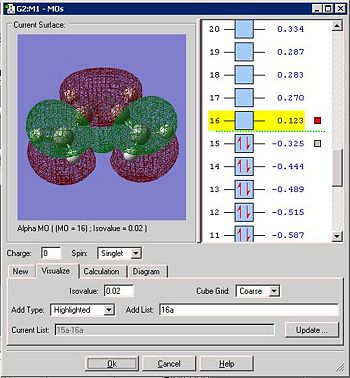
Below is the HOMO of the transition state:
The HOMO is antisymmetric with respect to the plane slicing the central carbons. By recognition of previous analysis it is the anti-symmetric HOMO of cis-butadiene that contributes and as there is a π* looking element in the ethylene fragment, it must mean that the LUMO of ehtylene contributes. This is intuitive though as, for the HOMO of the TS to be anti-symmetric, both the contributing MO's must be anti-symmetric also. A π* orbital is always anti symmetric on its own and unoccupied so it must be this rather than the ethylene HOMO (π orbital) that contributes. This reaction is allowed because both contributing MO's have the same symmetry properties and significant overlap of the orbitals can occur.
Maleic Anhydride and Cyclohexa-1,3-diene
All calculations were initally computed semi-empirically, but all results here were done via the B3LYP method to give greater accuracy and reliability for discussion.
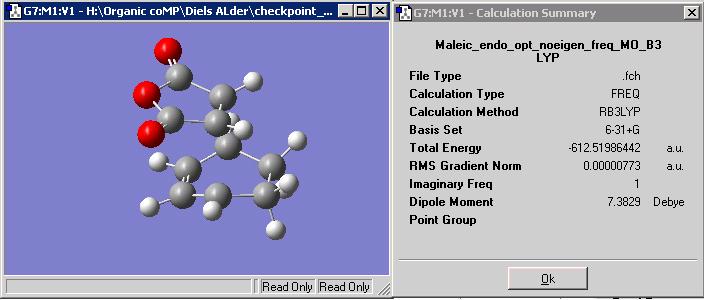
Structurally, the endo and exo form differ in the orientation of the maleic anhydride fragment. In the final product the endo form as the fragment facing 'down' in relative terms from the cyclohexene ring, while the exo form has the fragment facing 'up'. Analysis of the transition state allows one to speculate why such orientations occur.
By transition states the endo form:
has greater stability than the exo form
This is by roughly 3.07 kcal/mol
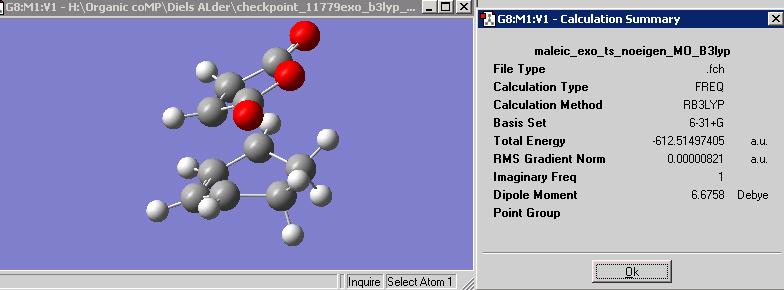
If we observe the orientation side on with the maleic anhydrdie on top, the endo transition strucuture has the carbonyl end of the maliec fragment parallel to the C-C double bond of the cyclohexene fragment below. Conversely the exo form of the maleic fragment is the opposite way round i.e. the carbonyl bonds are parallel to the opposite of the side of the C=C in the cyclohexane fragment. It can therefore be said then that difference in stability of the two forms is due to the orientations of the two fragments in the respective endo and exo transition structures.
If we are to concentrate solely on the structure of the exo form there is evident destabilisation that is not followed in the endo form. Namely this is the steric interaction between the carbonyl groups and the hydrogen sticking up from the cyclohexene ring directly below it. This is due to the difference in carbon hybridisation. As the cyclohexene carbons in question are sp3 hybridised, they are tetrahedral in geometry and therefore take up more space, pushing it's hydrogens closer to the planar sp2 carbonyl carbons of the maleic fragment directly above. This of course is an unfavourable steric interaction and destabilises the exo form. This is not experienced in the endo form however as the carbonyls are directly below sp2 carbons in a C=C bond which has it's hydrogens linearly facing away. This extra repulsion in the exo makes the form unfavourable even before the favourable interactions of the endo form are probed.
It is thought that the endo form is favoured due to secondary orbital overlaps. As can be seen by the geometry of the endo ts above, the carbonyl groups of the maleic fragment are direclty aboved the C=C bond of the cyclohexene fragment, without the steric interaction of the exo form. It can be said that there is an orbital interaction between the occupied C=C π orbital and the unoccupied π* of the C=O bond in the maleic fragment. The inter fragment distance is roughly 300pm so this would enable good space for interaction as the orbitals will be much closer in length due to the shape. It is not a direct transfer of electrons to form a new bond, rather a stabilising interaction, or 2nd order charge transfer, that lowers the energy of the transition state and as a result of the lowered T.S. makes the resultant product more stable than the product without such secondary orbital interactions in its T.S. i.e. the exo form.
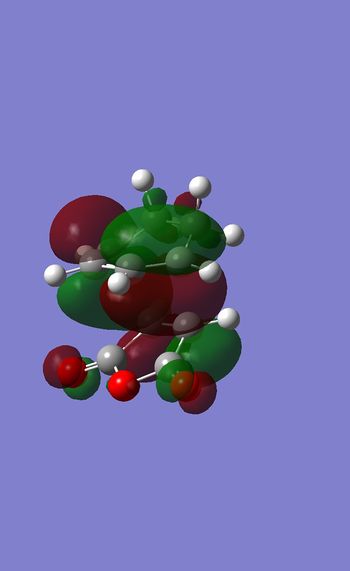
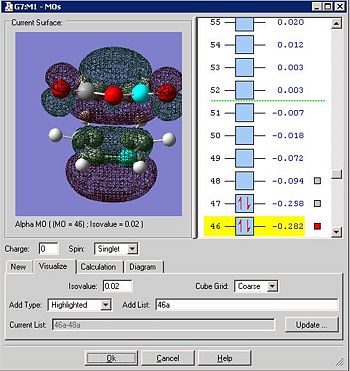
Below is the HOMO representation of the endo form by the B3LYP method
When the HOMO is investigated however, one struggles to actually visualise the C=O π* orbital. The orientations of the 3 MO's involved in the -C=O-CO-C=O- are in different orientations ( i.e. the C-O MO is horizontal which relates to lone pairs). The HOMO-1 clearly shows the C=C π orbital, but it is difficult to see how it can interact with the C=O π* when the latter is not in the HOMO or possibly not of the same symmetry. This follows a discussion by theoretical chemists such as Houk 3 that in fact there are no secondary orbital overlaps, but something else contributes to the prefered stability of the endo form. Perhaps it is due more to the destabilisation of the exo form due to repulsive interactions; i.e. it is not added stability but the destabilisation of another transition state which results in the preference of the endo form via its 'not de-stabilised' transition state.
This is a possible debate between organic chemists, who see the primitive chance of a secondary orbital overlap as a reason for added stabilisation, and computational chemists, who by performing actual calculations cannot spefically see any evidence for the plausible reasoning. If more time was possible one would perform an NBO analysis to ascertain whether there actually is any charge transfer of overlap between the C=C π orbital and the C=O π* orbital; this would provide a quantitative insight into the possible overlap, though one must speculate himself as to whether it is a real life possibility as to the constraints of a B3LYP calculation.
References
1. Fox, MA and JK Whitesell. Organische Chemie. 1994. Spektrum
2. "Periodic Table: Date of Discovery". Chemical Elements.com. Retrieved on 2008-12-13.
3. K. N. Houk, Joyner. Sims, R. E. Duke, R. W. Strozier, J. K. George, Frontier molecular orbitals of 1,3 dipoles and dipolarophiles, J. Am. Chem Soc., 1973, 95 (22), 7287-7301