Rep:Mod:bhheller
Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations
Benjamin Heller
Computational Lab Module 1
Introduction and Aims
This project is an investigation into the modelling of aspects of organic structure and reactivity, and such modelling can often be used not only to rationalise the outcomes of reactions, but to predict useful modifications or even new types of reaction. Two methods of calculation will be used; molecular mechanics method using MM2 and MMFF94 force field based models and a semi-empirical molecular orbital model - MOPAC PM6. These techniques will then be applied to a piece of scientific research of our own finding.
Modelling using Molecular Mechanics
Section 1. The Hydrogenation of Cyclopentadiene Dimer
Dimerisation of Cyclopentadiene
Cyclopentadiene dimerises to form dimer by a [4π+2π] Diels-Alder cycloaddition mechanism. It is an example of cycloaddition and there are no intermediate species. One of the reasons the Diels-Alder reaction goes so well is that the transition state containing six delocalised electrons and thus has some aromatic character and is therefore more stabilised. There are two possible products for this reaction; they are called endo and exo.

To determine their relative stabilities they were modelled and the energy was calculated. The results are tabulated below:
| Molecule | MM2 Energy kcal/mol |
|---|---|
| 1 | 31.8803 |
| 2 | 34.0000 |
The energy for the exo product is lower than that of the endo product and so is the more stable. However, the endo product is favoured and is the only one formed even though it is less stable than the exo product – it is the kinetic product. It is favoured as it's formation is quicker due to a lower energy transition state because of Secondary Orbital Interaction (SOI)[1] between the pz orbitals. This stereoselectivity was the basis of the Alder’s endo rule, also known as the principle of the maximum accumulation of unsaturated centres.
Hydrogenation

Compounds 3 and 4 are the products of the hydrogenation of one of the C=C double bonds in 2. Both compounds were modelled and the energies were calculated to determine the most stable (thermodynamic) product and hence the relative ease of hydrogenation of the two.
| Energies (kcal/mol) | Molecule 3 | Molecule 4 |
|---|---|---|
| Stretch | 1.2826 | 1.1058 |
| Bend | 19.8610 | 14.5314 |
| Stretch-Bend | -0.8380 | -0.5493 |
| Torsion | 10.8096 | 12.5098 |
| Non-1,4 VDW | -1.2180 | -1.0725 |
| 1,4 VDW | 5.6360 | 4.4955 |
| Dipole/Dipole | 0.1620 | 0.1406 |
| Total Energy | 35.6952 | 31.1614 |
According to Liu, Mi, Wang and Zhang 2 hydrogenates to the dihydro derivative 4 but not 3 and then eventually to the tetrahydro derivative:

The above results show that 4 is the most stable, with an energy of 31kcal/mol compared to 35kcal/mol for 3, and thus is the thermodynamic product and the most likely product in aggrement with the findings of Lui et al. The most substantial difference in energy between the two compounds was in the bending energy (19.9kcal/mol for 3 compared to 14.5kcal/mol for 4). This is due to the greater ring strain felt by the norborene C=C bond, compared to the cyclopentene C=C bond, owing to the bridging methylene group. This C=C double bond is more reactive than the cyclopentene double bond and hence is hydrogenated more easily as in the formation of 4.
Section 2. Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
This section consists of two reactions, both of which involve nucleophilic attack at the 4-position in the pyridine ring of a Nicotinamide adenine dinucleotide derivative. The optically active derivative of prolinol, N-methyl pyridoxazepinone, (5) reacts with methylmagnesium iodide to alkylate the pyridine ring at C(4). The methyl magnesium iodide is as a Grignard reagent where the methyl group acts as a nucleophile to attack the pyridine ring in a regio- and stereo- selective manner. the mechanism is shown below:


| Molecule 5 | |||
|---|---|---|---|
|
The high regio- and stereoselectivity for addition of Grignard reagents these prolinol derivatives may be a due to coordination between the electropositive magnesium in the Grignard reagent and the amide oxygen atom[2] as shown above and then conjugate delivery of the methyl from the magnesium to C(4) of the pyridine ring generates the magnesium enolate which is then eliminated to form 6. The energy of various conformations of 5 were determined to find the most stable one. Attention was paid to the geometry around the carbonyl and pyridine ring in each conformation as it is this arrangement that determines the stereochemical outcome of the reaction. The geometry was quantified by using the dihedral angle between the amide carbonyl and C(4) of the pyridine ring. The results of the measured dihedral angles and corresponding energies were plotted on the graph below:
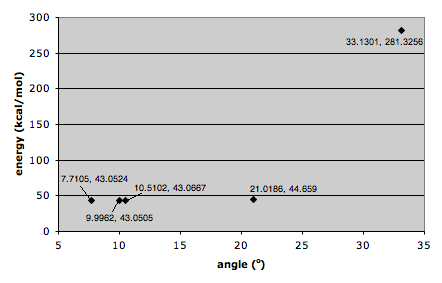
These results show that the molecule tends to exist with the oxygen of the amide group angled between about 10o and 22o from the pyridine ring, but crucially above the plane of the pyridine ring. this explains the stereochemistry of the product as the Grignard reagent coordinates to the oxygen during the reaction it attacks C(4) from directly above.
If the MeMgI is included in the optimisation calculation, the program gives the error message; MM2 is able to handle the Mg but the appropriate force field parameters are necessary. The Mg could have been included if another calculation method was used, ofr example the Gaussian or MOPAC methods. The MOPAC PM6 method would be much faster and so more practical than Gaussian.
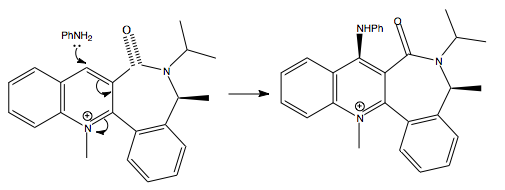
The reaction between PhNH2 (aniline) and N-methylquinolium (7) is also regio- and stereo- selective. The nitrogen atom with it's lone pair acts as the the nucleophile and also attacks at the C(4) position in the pyridine ring. The mechanism is shown below:
| Molecule 7 | |||
|---|---|---|---|
|
The amine attacks on the opposite face with respect to the C=O moiety leading to excellent diastereofacial selectivity, this originates from the steric control exerted by the carbonyl group[3]. The dihedral angles measure in the ChemBio3D model support this theory as the most stable conformer existed with the carbonyl group pointing about 20o below the pyridine ring so nucleophilic attack by the aniline is electronically and sterically hindered at the lower face of the ring so the aniline must attack the top face of the ring at the C(4) position instead.

These calculations were run using molecular mechanics force field model, MM2 which is a basic model that accounts only for sterics and lone pair interactions. More accurate calculations can be done using molecular orbital modelling, more specifically the MOPAC PM6 molecular orbital method or the Gaussian density functional theory (DFT), these methods as touched on earlier would also allow for the simultaneous calculation of more than one molecule. It is these molecular orbital based methods that are used later in the module.
Due to the size of the central ring in all of these molecules (7 carbons) the molecules are fairly flexible. This makes it harder to find the conformer with the lowest energy. Introducing sterically bulky groups (like a tert-butyl or a trityl) to lock the ring would make them less flexible as there would be a larger energy barrier between conformers. This would also improve the regio- and stereo- selectivity of reaction.
Section 3. Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
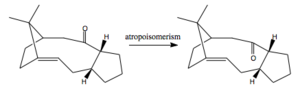
9 and 10 are key intermediates in the total synthesis of Taxol and the carbonyl group can point either up or down. According to Paquette[4], on standing 10 isomerises to 11, this is an example of atropoisomerism[5]. Atropisomerism is the distinction between two molecules that arises due to restricted rotation about a single bond, usually due to the high steric demand removing the usually free rotation.
The energies of the atropisomers were calculated using MM2 and then MMFF94 for comparison and the results are shown below:
| Energies (kcal/mol) | Molecule 9 | Molecule 10 | ||||||
|---|---|---|---|---|---|---|---|---|
|
| |||||||
| Stretch | 3.1830 | 2.7462 | ||||||
| Bend | 18.8526 | 15.8686 | ||||||
| Stretch-Bend | 0.3241 | 0.3578 | ||||||
| Torsion | 20.7519 | 17.4893 | ||||||
| Non-1,4 VDW | 1.1801 | 0.0876 | ||||||
| 1,4 VDW | 15.0245 | 12.8258 | ||||||
| Dipole/Dipole | -0.0541 | 0.0579 | ||||||
| Total Energy | 59.2621 | 49.4332 | ||||||
| Total Energy (MMFF94) | 82.7857 | 61.0339 |
The total energy of isomer 10 is 49.4kcal/mol, lower than that of isomer 9, which is 59.3kcal/mol. The most substantial difference in the constituent parts of the total energy is in the bending energy. 9 has significantly higher bending energy 18.9kcal/mol compared to 15.9kcal/mol in 10. This is because in 9 the cyclohexane ring is locked in the high energy twist-boat conformation due to the position of the carbonyl pointing above the ring. Whereas in 10 the cyclohexane ring exists in it's more stable, lower energy chair conformation as the carbonyl is below the molecule. There is also a significantly larger amount of torsional strain in 9 compared to 10. This could be due to the clash between the carbonyl and the bridging iso-propyl group. The two groups are furthest apart in 10 so the steric clash is less. As a result 9 will spontaneously isomerise to form 10 as shown in below.
Although significantly higher the results for MMFF94 show a similar comparison between conformers. The energies obtained are higher as a different force field is being used so similar values wouldn't be expected.
9 and 10 react much slower to hydrogenation than expected for strained alkenes due to a special stability because of the cage structure of the alkene. These type of stable molecules have been called hyperstable alkenes. Hyperstable alkenes or olefins are alkenes that are less strained than the parent saturated hydrocarbon and so show decreased reactivity. This is due to the bridgehead location of the double bonds[6]. A twisted olefin has reduced π overlap. This results in an increase of the HOMO energy and a simultaneous decrease of the LUMO energy. HOMO-LUMO degeneracy is reached when the twist angle becomes 90o (D2dsymmetry). They are characterised by having negative “olefin-strain” energy (OS), defined as the difference between the strain energy of an olefin and that of its parent hydrocarbon[6].
Modelling Using Semi-empirical Molecular Orbital Theory
The limitations of the molecular mechanics approach have been demonstrated and consideration must be taken of the electrons in molecules and how the electrons influence bonds and derived spectroscopic properties. In the following sections all models were minimised first using molecular mechanics (MM2) then minimised again using MOPAC PM6 molecular orbital method.
Section 4. Regioselective Addition of Dichlorocarbene
Orbital control of reactivity
Dichlorocarbene addition to 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene[7] shows remarkable π-selectivity, the mono-adduct (syn-trichloride) (72%) and the di-adduct (23%) are the only products isolated[8].
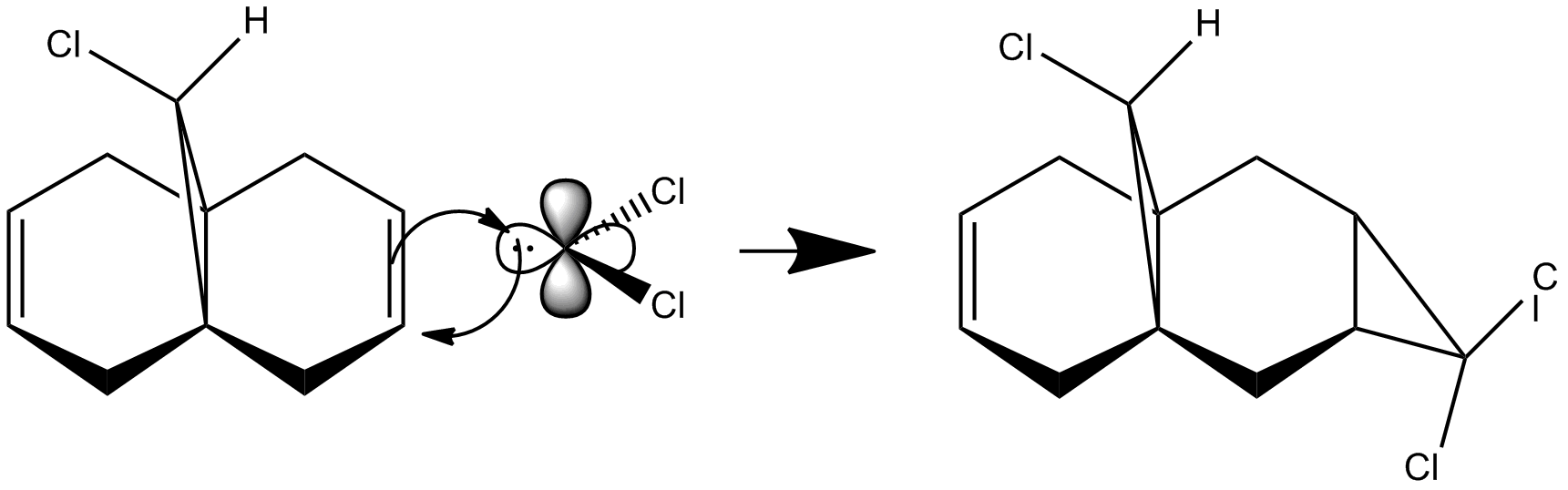
The reactivity and hence regioselectivity of a molecule is determined by its molecular orbitals, most importantly the frontier orbitals, the HOMO and the LUMO. The molecular orbitals were modelled using PM66 and they are shown below:
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
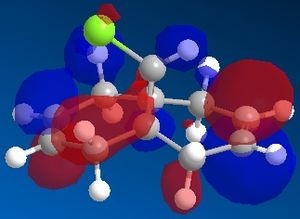 |
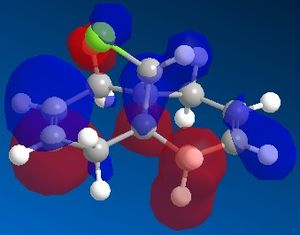 |
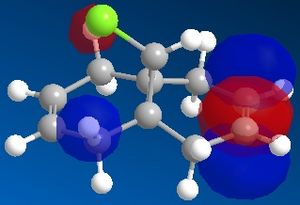 |
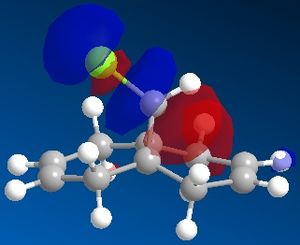 |
 |
It can be seen that the HOMO orbital is the syn-alkene π orbital and so the bulk of the electron density is located on the syn-alkene. As a result it is much more nucleophilic than the anti-alkene and as dichlorocarbene is an electrophile, it will attack the more electron-rich nucleophilic syn-alkene rather than the electron-poor anti-alkene and so the syn-adduct is favoured. The anti-alkene π orbital is the HOMO-1 orbital and so is at a lower energy than the syn π orbital so less likely to react.
There is also a stabilising antiperiplanar interaction between the C-Cl σ* orbital (LUMO+1) and the anti-alkene π orbital (HOMO-1) that causes anti-alkene π orbital to become lower in energy than the syn-alkene π orbital (HOMO) by 0.08eV[7]. As a result of this increased stability the anti-alkene π orbital is less reactive and will only react with a very aggressive electrophile. Any electrophile that would react with the anti-alkene would also react with the syn-alkene which explains why no anti-adduct is observed, only a small amount of the di-adduct.
Vibrational Frequencies
To calculate the influence of the Cl-C bond on the vibrational frequencies of this molecule 12 which contains a double bond anti to the Cl-C bond was compared to a hydrogenated version where this anti (or exo) double bond is replaced by a C-C single bond. The results were obtained using the B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation and the results are shown below:
| Derivative | Syn-alkene stretch | Anti-alkene stretch | C-Cl stretch |
|---|---|---|---|
| Di-alkene (12) | 1757 | 1737 | 771 |
| Hydrogenated monoalkene (syn-alkene) | 1758 | 775 | |
| Hydroxy group added | 1758 | 1753 | 765 |
| Cyano group added | 1757 | 1706 | 766 |
| Silyl group added | 1756 | 1690 | 764 |
The C-Cl stretching frequencies of approximately 770cm-1 correspond well with the literature value of 760cm-1[9]. However, the observed frequencies for the C=C bonds are substantially higher than those in the literature; 1640–1680cm-1[9] suggesting a stronger, more stable bond as a higher wavenumber corresponds to a higher energy, stronger bond. The frequencies are higher because they were calculated using an ideal harmonic oscillator but in reality, non-idealities exist and the stretches are anharmonic. Also, a relatively small basis set was used which is not as accurate. Calculations run with a larger basis set and with an anharmonic oscillator would have been more accurate but they are more complicated and take up more power and time. Hardly appropriate for an undergraduate lab.
Unexpectedly, the frequencies of the anti-alkene stretches are lower than those of the syn-alkenes which suggests that they have lower bond energy and are therefore less stable, seemingly in complete disagreement with the arguments above. However, owing to the fact that the stretching frequency depends on the strength of the entire bond, which for a double bond includes the π and the σ-bonds, in comparison with earlier where we were only discussing the stability of the π-bond, this does not actually contradict the earlier arguments as the π-bond can be unavailable for electrophilic attack but the whole bond can still have a lower energy. Thus the overall de-stability of the anti-alkene bond must be explained by either effects in the σ-bonds or an inherent destabilising effect in the entire molecule as it is not due to the π-bonds.
The stretching frequency of the syn-alkene in both the di-alkenene and the monoalkene and with the substituents remains constant, suggesting that the anti-alkene does not affect the strength of the syn C=C bond.
This experiment was furthered through the addition of substituents onto the anti-alkene to see the effects on the C=C and C=Cl stretching frequencies. The addition of these substituents (OH, SiH3 and CN) substantially changed the frequencies of both the C=C and C-Cl bonds. This is, unsurprisingly, most marked in the anti-alkene where the groups were substituted.
The addition of the silyl group lowers the frequency the most despite the fact that silicon is more electropositive than carbon. This could be due to promotion of electron density form the C=C bond into some of the available d-orbitals on the silicon, thus weakening the C=C bond. The lower frequency for the cyano-substituted alkene is most likely due an inductive electron withdrawing effect removing density from the C=C bond. Addition of the hydroxy group to the alkene results in a higher C=C frequency as, although oxygen is more electronegative and so inductively withdrawing, it is a stronger resonance donator and so donates electron density to the C=C bond, strengthening it.
Both the di-alkene and the hydrogenated mono-alkene belong to the Cs symmetry point group and so they both possess a plane of symmetry perpendicular to the principle axis of rotation (σh).
Structure based Mini project using DFT-based Molecular orbital methods
Structural revision of the Mycobacterium tuberculosis-produced diterpene, edaxadiene
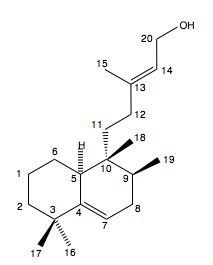
In this paper by Spangler, Carson and Sorensen[10] significant discrepancies were found between the spectroscopic data obtained for the synthetic construct of a pathogen crucial for the infectivity and virulence of M. tuberculosis (edaxadiene) and the natural isolate. This raised questions about the structural assignment of edaxadiene. A structural reassignment was carried out followed by a total synthesis of the correct structure of the natural product (nosyberkol). The synthesis of nosyberkol contains a biomimetic conversion of tuberculosinol, an isomer of nosyberkol, into nosyberkol.
The proposed structure of the pathogen was thought to be edaxadiene[11][12] (shown below) but during it's synthesis, similar structures were found to have significantly different 13C NMR shifts for the C(13) atom. The structures they synthesised had shifts closer to 42ppm rather than the 72.9ppm shift reported.
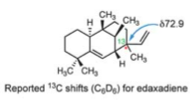
Optimisation of the reported structure of edaxadiene using MM2 then MOPAC PM6 and subsequent calculation of the 13C NMR produces the following results. Also tabulated are the corresponding shifts for nosyberkol (the actual structure of edaxadiene) and tuberculosinol (to be used later).
| Carbon atom | edaxadiene shifts (ppm) | nosyberkol shifts (ppm) | tuberculosinol shifts (ppm) |
|---|---|---|---|
| 1 | 27.7 | 26.5 | 27.7 |
| 2 | 44.0 | 42.9 | 43.5 |
| 3 | 39.7 | 41.1 | 42.5 |
| 4 | 141.7 | 145.0 | 135.4 |
| 5 | 52.5 | 48.0 | 44.3 |
| 6 | 36.4 | 34.0 | 37.1 |
| 7 | 124.8 | 115.6 | 126.8 |
| 8 | 42.9 | 32.6 | 34.9 |
| 9 | 42.9 | 34.9 | 39.9 |
| 10 | 38.3 | 41.2 | 42.9 |
| 11 | 39.8 | 36.9 | 40.5 |
| 12 | 36.8 | 36.4 | 39.9 |
| 13 | 46.4 | 74.0 | 64.9 |
| 14 | 144.4 | 146.1 | 143.2 |
| 15 | 21.4 | 23.9 | 24.1 |
| 16 | 30.1 | 31.0 | 30.5 |
| 17 | 27.3 | 27.8 | 27.8 |
| 18 | 27.3 | 23.4 | 22.7 |
| 19 | 18.7 | 19.7 | 19.5 |
| 20 | 105.9 | 110.3 | 113.5 |
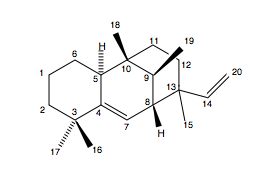

The important shift is that for the C(13) as it is this carbon that was found to change most between the two molecules. It can be seen that there are very significant differences between the shift for edaxadiene (46.4ppm) and the reported 72.9ppm. In fact the shift for nosberkol (74ppm) is very similar to the reported value and it was upon the synthesis and determination of the NMR of this compound that lead Spangler et al. to reassign the structure of edaxadiene to that of nosyberkol. The peak for nosyberkol is significantly more upfield than the peak for edaxadiene due to the presence of the hydroxy group. An independent synthesis of nosyberkol unambiguously established this structural revision[13].
In fact this structural reassignment could have been done purely using computational modelling methods and need not have taken synthesis and subsequent NMR determination to realise the incorrect structure especially seeing as the initial structure was so incorrect.
| edaxadiene | nosyberkol | ||||||
|---|---|---|---|---|---|---|---|
|
|
Once they had decided that the correct structure was nosyberkol, a total synthesis was devised. Within that synthesis was a step where there was a biomimetic conversion of tuberculosinol into nosyberkol by treatment with a mixture of copper(II) chloride and N,N-dicyclohexyl-carbodiimide (DCC) which was of particular interest to the authors. The total synthesis scheme is shown below.
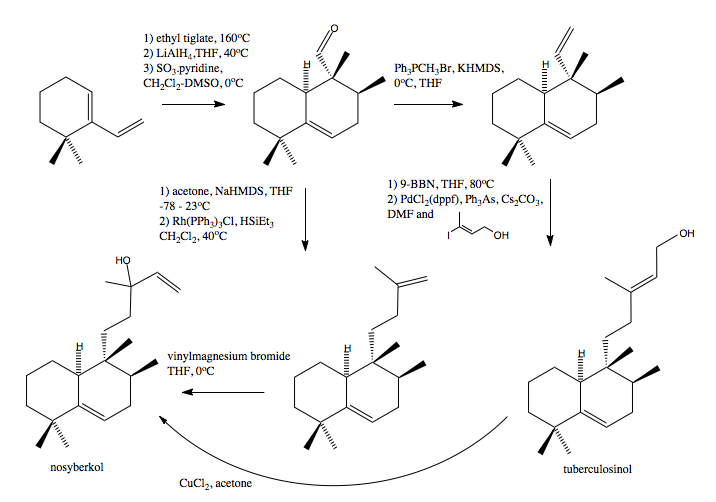
Using ChemBio3D we can differentiate between the two isomers and so determine whether or not the reaction was a success. The 13C NMR peaks are tabulated above and the differences in the peaks between the two isomers are shown on the graph below.
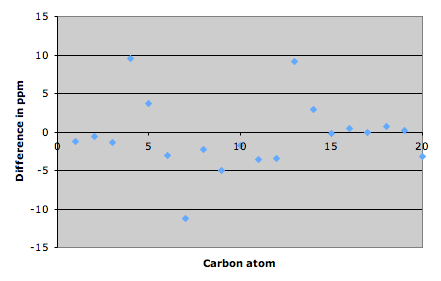
There is a large difference between the shifts for the C(13) atom as expected as in nosyberkol the C(13) atom is sp3 and in tuberculosinol it is sp2 and so is shifted further upfield. There is also a hydroxy group attached to this carbon further deshielding it and shifting it more. C(20) is shifted further upfield in tuberculosinol due to position of the hydroxy group. The other differences at carbon atoms 4, 5, 6 and 7 are most likely due to the conformation of one of the molecules being slightly different at the boundary of the two cyclohexane rings.
The IR spectra of the two isomers would also show a difference as in one (nosyberkol) there is a tertiary alcohol and the other (tuberculosinol) there is a primary alcohol although this difference would be quite small.
| tuberculosinol | |||
|---|---|---|---|
|
In conclusion molecular modelling is a very useful way of predicting and analysing molecules and their reactions and as a result these two isomers can be easily distinguished using said techniques. However one must aware of the limitations of each piece of software.
References
- ↑ P. Caramella, P. Quadrelli, L. Toma. J. Am. Chem. Soc. 124, 7, 2002[1]
- ↑ A.G. Shultz, L. Flood et al. J. Org. Chem., 1986, 51, 838 [2]
- ↑ S. Leleu et al. Tetrahedron: Asymmetry, 2004, 15, 3919. [3]
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319[4]
- ↑ L. A. Paquette. Stereocontrolled Construction of Complex Cyclic Ketones via Oxy-Cope Rearrangement. Angew. Chem. Int. Ed. Engl. 29 (I990) 609-626[5]
- ↑ 6.0 6.1 W. F. Maier, P. v R. Schleyer. Evaluation and Prediction of the Stability of Bridgehead Olefins. J. Am. Chem. Soc., Vol. 103, No. 8, 1981[6]
- ↑ 7.0 7.1 B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447[7]
- ↑ B. Halton, S. G. G. Russell. J. Org. Chem., Vol.56,No.19, 1991[8]
- ↑ 9.0 9.1 IR Correlation Table[9]
- ↑ J. E. Spangler, C. A. Carson, E. J. Sorensen. Chem. Sci., 2010, 1, 202–205
- ↑ F. M. Mann, M. Xu, X. Chen, D. B. Ulton, D. G. Russell and R. J. Peters, J. Am. Chem. Soc., 2009, 131, 17526–17527
- ↑ F. M. Mann, S. Prisic, H. Hu, M. Xu, R. M. Coates and R. J. Peters, J. Biol. Chem., 2009, 284, 23574–23579
- ↑ Maugel, F. M. Mann, M. L. Hillwig, R. J. Peters and B. B. Snider, Org. Lett., 2010, 12, 2626–2629
