Rep:Mod:bghweg223
The Cope Rearrangement
The aim of this computational experiment is to investigate the [3,3]-sigmatropic shift of 1,5-hexadiene, also known as a Cope Rearrangement.
Scientific consensus is that the rearrangement occurs in a concerted pericyclic manner through either a chair or boat transitions state.
To fulfil the aims of the experiment the low-energy minima (conformers) and the pericyclic transition structures, chair and boat, for the Cope rearrangement need to be determined on C6H10 energy surface. XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Optimising the Reactants and Products
The first step is this computational experiment is to find the optimised structures for the reactants and products. For the Cope Rearrangement of 1,5-hexadiene, the reactant and product are both 1,5-hexadiene. However, the position of two π bonds and one σ bond have changed, which is important for substituted 1,5-hexadiene derivatives.
1,5-hexadiene has 3 C-C's in the middle it's chain. There is free rotation about σ-bonds and therefore 1,5-hexadiene has the ability to adopt many different conformers (local low-energy minima). The task is therefore to find the lowest energy conformer, which is the conformer which will be most populated.
Finding Conformers of 1,5-Hexadiene
To start the investigation with the lowest energy conformers of 1,5-hexadiene some simple conformational analysis can be applied. It is well known that butane has two thermally accessible conformers gauche and anti-peri-planar (a.p.p.). Therefore, the four central carbon atoms of 1,5-hexadiene can have their dihedral angles manipulated to app & gauche conformations, then their conformations can be optimised and the energies compared, see below for results.
The computational level of theory used to optimise the structures is Hartree-Fock with the basis set 3-21G (HF/3-21G). This is a relatively low end method for calculations and is used to gain a quick and cheap results.
It can be seen by comparing the relative energies for both conformers that the a.p.p. conformer is lower in energy. This is perhaps the expected result as the two most sterically demanding groups are as far apart as possible.
Finding lowest energy conformer of 1,5-hexadiene
In the above a.p.p. conformer the -CH=CH2 groups are still both on the same side of molecule, with respect to the plane of the C-C-C-C bond, therefore perhaps the energy could be lowered by positioning the alkene groups on opposite sides. The results for which are shown below.
It can be seen that this adjustment to the relative positioning of the alkene groups lead to a slight increase in the conformers energy. One could therefore assert with reasonable confidence that A.p.p. C=C same side (A.p.p. C2) is the lowest energy conformer for 1,5-hexadiene.
Comparison of calculated conformers to Appendix 1
Provided in the instructions is Appendix 1 which shows the energy and conformers for 1,5-hexadiene, the results from above can be then compared to those from Appendix 1.
| Calculated label and point group |
Calculated energy | Appendix 1 label and point group |
Appendix 1 energy |
|---|---|---|---|
| A.p.p. C2 | -231.69260 | anti1 | -231.69260 |
| A.p.p. Ci | -231.69254 | anti2 | -231.69254 |
The Gauche conformation included in tables previously is not included in Appendix 1, because it's energy is too high to make it into the 10 lowest energy conformers. In constrast, both the a.p.p C2 and Ci, were in the lowest 10, and shall be referred to as anti1 and anti2 respectively from now on. The energies of anti1 and anti2 match well between the calculations and the appendix. Showing that the calculations above have been performed correctly and that the HF/3-21G method can return consistent and repeatable results and therefore is likely to be adequate for this investigation. The most interesting observation from the Appendix 1 is that a gauche conformer has the lowest energy! This at first appears to be counter-intuitive as one would expect a a.p.p. conformer to be lowest energy due to steric reasons discussed previously. Therefore it is likely that the low energy gauche conformer favourable electronics interactions are also involved. XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Comparison of computational methods in optimising anti2 conformer
The anti2 conformer (a.p.p. Ci) shall now be optimised by a more computationally demanding method DFT-B3LYP with basis set 6-31G*. The geometries of the anti2 conformers shall then be compared.
| Geometry parameters | HF/3-21G | B3LYP/6-21G* | ||||
|---|---|---|---|---|---|---|
| Structure | ||||||
| C9-C1-C4-C7 dihedral |
180.0o | 180o | ||||
| C11-C9-C1 dihedral |
124.8o | 125.3o | ||||
| C11-C9 bond length |
1.316Å | 1.333Å | ||||
| C9-C1 bond length |
1.508Å | 1.504Å | ||||
| C1-C4 bond length |
1.553Å | 1.548Å |
From initial inspection of the Jmol file it can be seen that both methods return geometries which are very similar. Upon comparing the bond angles and lengths is becomes clear that the structures are about 99% identical with only small deviations. Therefore, it can be concluded the HF/3-21G method is sufficient for the comparisons of geometries for the 1,5-hexadiene.
Frequency analysis of anti2 conformer
Finally, to check that that the anti2 conformer is in fact a conformer (low-energy minima) one must perform a frequency analysis to check that all the vibrations are real (positive). This was perform on anti2 conformer using B3LYP/6-21G*.
The low frequencies from the calculation were -
Low frequencies --- -18.6342 -11.7125 -0.0009 -0.0006 0.0003 1.8424 Low frequencies --- 72.7326 80.1452 120.0243
Since in the second row there are no negatives frequencies the anti2 conformer is a minima. The simulated spectra and the vibrations that appear in the spectra are shown below.

This simulated spectra can then be compared to a literature spectra[1]. Below is a table comparing calculated shifts to the literature ones.
| Calculated peak (cm-1) |
3234 | 3155 | 3137 | 3031 | 1734 | 1523 | 1289 | 1036 | 940 | 938 | 669 |
| Literature peak (cm-1) |
3079 | 2983 | 2925 | 2848 | 1646 | 1441 | 1214 | 998 | 914 | 914 | 652 |
From the above tabulated data it appears that all the IT active vibrations in the calculated model have corresponding peaks in literature IR spectra. The spectra of comparison look similar and have similar patterns such as the unusual peak at ~1700cm-1 and 4 distinct C-H peaks (~3000cm-1). However, all the calculated peaks are significantly larger than the literature values. With the greatest values having the largest difference of ~7.5% and the smallest values being 2.5% larger. This is a systematic error in the calculation that comes from the method treated the vibrations as harmonic oscillators. To calculate a more accurate spectra a anharmonic model must be used.
From the calculation it is also possible to find information about the energy of the conformer. The most important thermochemical information is included below.
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Optimising the "chair" and "boat" transition structures
In this part of the experiment the transition structure will be investigated using a number of techniques, the reaction coordinate visualised and the activation energy calculated for both the "chair and "boat" transition structures.
Optimisation of transition state fragment
The transition states of the Cope rearrangement for 1,5-hexadiene are thought to be aromatic and progress as indicated by the image[2].

In the diagram above it can be seen that both transition structures progress with bond breaking/forming occurring inbetween two allyl fragments (CH2CHCH2). To model the transition structures this fragment must first be optimised. The fragment was optimised using HF/3-21G level of theory (which shall be applied throughout the transition state optimisations), which yielded the following structure.
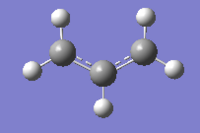
Manual optimisation of "chair" transition state using TS(Berny)
The "chair" transition state can be found manually by using optimisation to a maximum. This is done by the calculation of the force constant matrix (the Hessian). At the maximum stationary point negative imaginary frequencies appear, this frequency should correspond to the Cope rearrangement.
To perform the manual "chair" transition state optimisation the allyl fragment was put into the Gaussview window twice. The fragments were then orientated so that they looked similar to the "chair" transition state. Using HF/3-21G level of theory they were Optimised to a TS (Berny).
It is vital to the this method of finding transition states that the fragments are orientated in a good guess transition structure. Otherwise,the method will not be able to find the correct TS due to farthe curvature of the potential energy surface being different at points far away from the maxima. In this case the terminal allyl carbon were placed ~2.2Å from the other terminal carbon.
The method provided the result with the following transition structure and imaginary frequency.
"Chair" transition structure (HF/3-21G - TS Berny)
|
"Chair" Cope rearrangement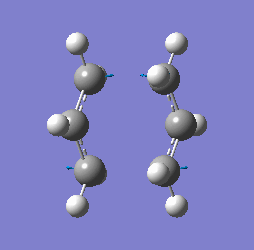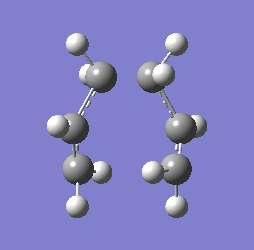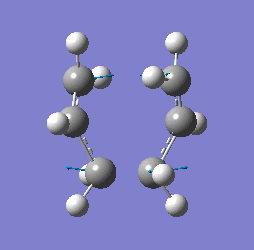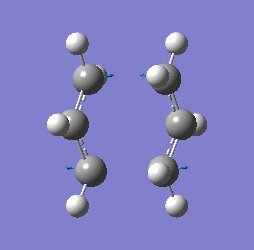 |
Manual optimisation of "chair" transition state using frozen coordinate method
In this method of manual TS optimisation the reaction coordinate is frozen and the rest of the molecule fully relaxed. Then the reaction coordinate is unfrozen and the transition state found. An advantage of this method is that it can avoid calculation of entire force constant matrix and instead differentiating along the reaction coordinate, resulting in a cheaper alternative to force constant matrix when it is expensive to compute.
To apply this method the terminal allyl carbons were set as a bond of fixed distance 2.2Å with frozen coordinates. The structure was then optimised giving a pseudo transition structure, i.e. it was like the TS except the bond breaking/forming distance had been frozen to 2.2Å. Next this constraint was removed and the optimisation set to run TS (Berny) as before but the Hessian was not calculated. The result of the calculation can be seen below.
"Chair" transition structure (HF/3-21G - Frozen coordinate method -TS Berny)
|
"Chair" Cope rearrangement XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX |
Comparison of the two manual transition structure optimisation methods
The two methods provide identical results, to the degree of accuracy of such calculations. All terminal carbon inter-fragment distances, bond breaking/forming, distances are 2.02Å. Also, the central carbon inter-fragment distance at 2.88Å and the fragment bond angle is 120.5o .The results are identical, showing that the two methods found the same maxima on the potential energy surface. This result is expected as the same level of theory and method were used to find the TS, the only real difference in the method was how the fragment were initially orientated to one another.
Optimisation of "Boat" transition structure using QST2 method
A fully automated method of findiug transition structures is the QST2 method. This method shall be applied to the 1,5-hexadiene, the calculation works by taking both the products and reactants of a reaction and interpolating between the structures in an attempt to find a transition structure.

To apply this method both product and reactant structures are drawn into one Gaussview MolGroup. From this window the atoms are numbered so that the numbering shows the Cope rearrangement occurs. The QST2 method was then applied. This method failed to find the correct "boat" transition state. To help the QST2 find the TS, the structure of the reactant and product can be changed as to match better match the "boat" conformer (and TS sown in image previously). By improving the initial guess it increases the chances of the chance of the automated method of finding the TS. The reactant, transition structure are provided below.
| "Boat" reactant |
"Boat" TS |
"Boat" Product |
Following potential energy surface (PES) from transition structures to local minima
Following PES by inspection
The next step in understanding the Cope rearrangement is to know which conformers have access to the transition states.
On inspection it is hard to tell which conformers lead to the transition structure. Or in terms of the PES, which low energy minima and maxima are thermally accessible to one another. For the "chair" transition state, it is possible to imagine the transformation from conformer to transition state. When looking down the plane of the two chains, imagine pulling apart the bottom set of terminal carbons whilst pushing the top pair closer to give a structure similar to that of similar to that of gauche2 (if we ignore the double bond.For the "boat" transition state if you imagine looking down one of the bonding breaking/forming interactions and then rotating about the interaction, until you two fragments are a.p.p. to one another you get the anti2 structure.
| Transition state | Conformer | |||
|---|---|---|---|---|
Chair transition state
|
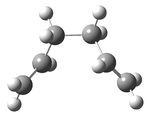 | |||
|
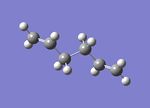 |
The above thought experiments show that it is possible to finding routes between conformers and transition states by looking. However, it is very hard to accurately estimate the energy barrier of such thought transformations. Therefore to get an accurate picture of which and how conformers transform into transition states a computational approach must be taken.
Following PES using Intrinsic Reaction Coordinate
This method automatically alters the geometry of the transition structure so as to follow the PES along where the gradient the steepest.
The calculation is set up to follow the symmetrical reaction coordinate (product & reactant are the same) in only one direction, included frequency analysis and with 50 points along the IRC as to give it enough steps to find the minima.
IMAGES OF SURFACE, MOTION + WRITE ABOUT OTHER METHODS AND ONE WITH ONLY 10
Diels-Alder Cycloaddition
Diels-Alder (DA) is a subclass of cycloadditions, which themselves are a type of pericyclic reaction. Specifically DA reactions are π4 + π2 cycloadditions. An example of which is the reaction of cis-butadiene and ethylene. DA reactions occur due to the favourable interaction between the HOMO-LUMO of the two reactants.

Frontier orbitals of butadiene and ethylene
The interactions of the cis-butadiene's HOMO and ethylene's LUMO and cis-butadiene's LUMO and ethylene's HOMO are vital to the sucess of the DA reaction. These MO's can be computed for both reactants.

Initially the semi-empirical AM1 method was used to optimise the structure of cis-butadiene. At first the structure of cis-butadiene was drawn planar with the dihedral angle C1-C4 = 0o. The structure was optimised and this gave the negative frequency. The imaginary frequency shows the molecule twisting as to lose it planar structure. The molecule was then re-optimised with the C1-C4 dihedral angle set to ~20o. At this point the method was switched from the AM1 method to B3LYP/6-31G* level of theory to get a more accurate result for the optimisation and molecular orbitals. The same process was then repeated for the ethylene molecule.
From the above symmetry assignment it can be seen that the HOMO and LUMO from each reactant have the same symmetry (anti- or symmetrical) they therefore interact and a cycloaddition could occur.
Transition structure of the Diels-Alder reaction between cis-butadiene and ethylene
The symmetry of both the HOMO & LUMO of the transition state are both symmetric. This result is expected from the HOMO and LUMO of the reactants. Two symmetric wavefunctions mixed result in a symmetric wavefunction; and two anti-symmetric mixed result in a symmetric wavefunction.
sp3 C-C bond length is 1.54 Å and a typical sp2 C=C bond length is 1.34 Å[6]
The Van der Waals radius of a C-atom is 1.72 Å[7]
References
- ↑ http://www.acros.com/
- ↑ E. Brown, R. Bader, and N. Werstiuk, J. Phys. Chem. 2009, 113, 3254
- ↑ http://www.ch.ic.ac.uk/wiki/index.php/Mod:phys3#Appendix_2
- ↑ http://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ http://www.ch.imperial.ac.uk/wiki/index.php/Mod:phys3#Appendix_1
- ↑ G. Schultz, I. Hargitta, J. Mol. Struc., 1995, 346, pp. 63-69
- ↑ M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer, D. G. Truhlar, 1995, 346, pp. 63-69