Rep:Mod:bg1512

Transition Structures - 3rd Year Computational Module

Bjorn Gugu (00757392)

This is the wikipage for the 3rd Year Computational Module "Transition Structures" report by Björn Gugu. The research and all other work contributing to this wiki are scheduled for the timeframe of 27/10/2014 - 07/11/2014.

Abstract

Transitions states for the Cope rearrangement and two Diels-Alder reactions were computationally investigated. Two plausible transition states for the Cope rearrangement were found, one chair shaped of symmetry C2h and one boat shaped of symmetry C2v. The chair transition state could be evaluated as the lower energy transition geometry and experimental activation energies were recovered to within 10%. The transition states for two archetypal Diels-Alder Reactions were calculated, discussing the effects of attack trajectory, orbital symmetry and secondary orbital stabilisation.

Introduction

Transition State Theory

The study of chemical reactions and mechanisms is inherently linked to the energy profile of reactants, products and that of their interconversion. While the thermodynamic reaction direction of a reaction can be easily predicted by invoking the net change of free energy in a conversion from products to reactants, a detailed study of chemical mechanisms is tied to the understanding of the energy profile during the reaction. A simple model for such an energy profile is that of the reaction coordinate. The reaction coordinate is a hypothetical measurement of the progress of a reaction. Displaying the free energy as a function of this coordinate often reveals that an interconversion firstly passes through a maximum of energy before resolution.

The development of potential energy surfaces ("PES") - multidimensional functions of energy vs. nuclear distances - allowed for a more succinct interpretation of the reaction coordinate. For a given PES, the series of nuclear arrangements which afford the overall lowest potential energy barrier is then defined as the reaction coordinate. The geometry of highest energy along this pathway - often called the activation energy - is termed the transition state ("TS"). It is therefore a saddle point in the potential energy surface: A maximum on the reaction coordinate, while also a minimum on the PES. As the number of participating atoms in a reaction increases, more degrees of freedom are introduced, which complicate the PES. This leads to the possibility of multiple reaction coordinate for a given reaction and therefore multiple TSs. While each pathway is a valid mechanism, many will differ from one another. It is these differences that correspond to multiple mechanisms and phenomena such as secondary orbital interactions. The importance of a proper understanding of the TS is evident and will be the subject of this report.

Quantum Chemistry & Molecular Modelling

Calculation of PESs requires a profound understanding of the underlying interactions between atoms. A quantum mechanical system such as a molecule may be entirely described by the Schrödinger equation:

$\hat{H}\psi =E\psi$

Where $\hat{H}$ is the Hamiltonian, an operator describing the energy of a wavefunction $\psi$ and $E$ is the energy eigenvalue of the wavefunction. Acceptable wavefunctions for electrons take the form

${\psi }_{n,m,l}=R_{n,l}(r)Y_{l,m}(\theta ,\varphi )\chi$

where $R$ denotes the radial component, $Y$ a spherical harmonic - the angular components - and $\chi$ the spin function of an electron. Such a wavefunction describing an electron is an orbital, a region of space in which the probability of finding an electron is almost unity. This equation is only analytically soluble for one-electron systems. In order to calculate multi-electron systems a number of approximations must be made. The first and foremost is the Born-Oppenheimer approximation, which treats electronic motion as independent of nuclear motion and therefore allows for nuclear charge to be treated as a static potential. Even so, the calculation of energies from this expression yields the general formula

$E=\frac{\int {\psi }^{*}\hat{H}\psi d\tau }{\int {\psi }^{*}\psi d\tau }$

in which the integrals require computationally expensive numerical solutions. In order to alleviate this problem, the electron wavefunctions are approximated. A collection of such modified wavefunctions is called the basis set of a calculation and allows for a compromise between computational effort and level of theoretical depth. Linear combinations of basis set orbitals then yield molecular orbitals (MOs), which are extensively used for the prediction of chemical and structural behaviour of species. Such approximate wavefunctions take the form of modified hydrogen wavefunctions - which are analytical - of which a common form are Slater type orbitals. However, these wavefunctions may not need satisfactory results and are often replaced by products of Gaussian functions. The computational methods in this report base entirely on the above described principles.

The Cope Rearrangement

The reaction scheme of the Cope rearrangement.

The reaction scheme of the Cope rearrangement.

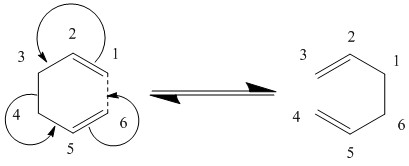
The Cope Rearrangement is a notable pericyclic reaction. This [3, 3]-sigmatropic shift has been the centre of mechanistical discussion for decades, ultimately leading to the question whether the transition state of such a reaction is concerted or step wise. Both pathways seem theoretically plausible; the first involves a six-atom TS stabilised by delocalised electrons, the latter invokes a diradical pathway. Experimental estimations of reaction energies and kinetics could establish that delocalised, or in other words "aromatic", TSs are most likely.

To this date, the Woodward-Hoffmann rules serve as the theoretical framework for pericyclic reactions. Invoking orbital symmetry arguments, they predict that a thermochemical 4n+2 electron reaction (such as the Cope rearrangement) passes through a Hückel-type ("aromatic") TS. However, two possible structures may be imagined, a chair-like structure of C2h symmetry and a boat-like structure of C2v symmetry. This computational experiment will provide estimations of transition state energies and thereby establish the most likely transition state geometry.

The Diels-Alder Cycloaddition

The reaction scheme for the reaction of butadiene and ethene to yield cyclohexene.

The reaction scheme for the reaction of butadiene and ethene to yield cyclohexene.

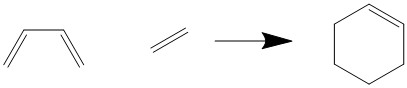
The Diels-Alder cycloaddition is probably the most archetypal of all pericyclic reactions. Systematically a thermal [4+2] - cycloaddition, two sigma bonds are formed at the expense of two pi bonds in its forward direction. Typically the reactants are an electron rich diene and an electron deficient dienophile. It should be noted that this reaction is entirely fueled by the interaction of pi-bonds and therefore the preferred attack angle will be close to π. While the reaction is stereospecific, still two possible isomers may be obtained. They are classified by their transition state geometry: The endo product is formed by an alignment of the two reactants in a seemingly parallel fashion, whereas the exo product results from the transition state geometry of least steric strain. While the exo product is the thermodynamically preferred product (due to lack of steric strain), the kinetic endo product often dominates because of secondary orbital interactions stabilising the TS. Practically, these two reaction pathways are characterised by different trajectories - the dienophile may attack the diene from the top or bottom face.

Further considerations about the reactivity of a given set of reactants in a DA-reaction include the need of the diene to be in a cis conformation. For alkene chains, such as 1,3 - butadiene, this conformation is hardly populated, leading to marginal reaction rates. Secondly, the electronic properties of a simple dienophile, such as ethene, often inhibit an effective reaction.

Two DA - reactions will be investigated in this experiment. The first is the prototypical reaction of 1,3 - butadiene with ethene to yield cyclohexene, which is a hardly reactive reaction in natural conditions due to the reasons listed above. The second on the other hand is a widely used reaction in which the highly electron deficient dienophile maleic anhydride is coupled with the reactive cyclohexadiene - it is bound to the cis-configuration due to its ring structure. Maleic anhydride is known to exhibit strong secondary interactions, favouring the endo product. This stabilisation is caused by the sterically unobstructed mixing of the C=O antibonding orbital with the π* of the diene.

A sketch of the orbital interactions in the DA reaction of maleic anhydride and cyclohexene. The dotted lines represent the additional MO mixing responsible for the endo-effect.

Methods

All calculations were conducted using the Gaussian09 software package and the associated visualisation program GaussView 5.0. The used level of theory for any given calculation will be specified in the text via []-brackets.

Results & Discussion

The Cope Rearrangement

Optimisation of Reactants

Firstly, the reactants and products - which possess an inherently equivalent structure - were optimised. A number of initial guesses, varying in conformation, were successfully optimised [HF/3-21G], yielding different conformers which could be assigned to previously identified conformations. The first isolated conformer is one of purely app linkages. It possesses C2h symmetry and an energy of -231.68539619 a.u.. It does not correspond to any of the reference structures. Second, a conformer of Ci symmetry and E = -231.69253528 a.u. was isolated, corresponding to structure "anti2". Next, a gauche conformer of C1 symmetry and E = -231.69266120 a.u. was found. This structure is a perfect match for "gauche3". Lastly, the lowest energy conformation (denoted "gauche2", symmetry C2, E = -231.69237280 a.u.) was found, clearly refuting the general notion of anti-periplanar conformations being the lowest in energy. It may be argued that anti-periplanar conformations do not only minimise steric strain, but also benefit from σ-σ* hyperconjugation and are therefore energetically most favourable. However, chains of increasing length accumulate additional van der Waals - interactions which can favour a more convoluted chain folding. It should also be noted that the energy difference between the "gauche2" conformers and the second most stable conformer is minimal, which further hints at an only marginal contribution of such secondary interactions.

Of these initial guesses, the "anti2" structure was chosen for further calculations. In order to certify the credibility of this structure, it was further optimised [DFT/B3LYP/6-31G*]. The overall geometry was not affected, the molecule still possesses Ci symmetry. However, the length of all bonds changed, assigning bond lengths more closely related to experimental values to all bonds. The double bond length was altered from 131.613 pm to 133.350 pm, while the single bond length changed from 155.275 to 154.816. The literature value for double bonds is 134 pm and that of single bonds 154 pm. Clearly, the newly optimised TS structure shows better agreement with reality than the low level optimisation. This affected the total energy, lowering it substantially to -234.61171063 a.u.. A frequency calculation showed furthermore that all vibrational modes possess real frequencies. Moreover, the associated predicted IR spectrum shows the expected peaks for C-H and C=C interactions. The vibrational calculation also allows for a range of data to be collected: The sum of electronic and zero-point energies equals -234.469219 a.u., the temperature correction to 298K alters this to -234.461869 a.u., the addition of thermal enthalpies raises it to -234.460925 a.u., while finally the free energy is -234.500809 a.u..

Location of transition states

In order to approximate the transition state of the Cope rearrangement, a number of techniques were employed. Firstly, a chair-like transition state was approximated by alligning two allyl fragments [HF/3-21G]. The delocalised nature of the allyl fragments lends itself to the calculation of an aromatic transition state in which all participating electrons are delocalised. Furthermore, it can be assumed that the TS is highly symmetrical due to the concerted and synchronous nature of pericyclic reactions, which is mirrored by two symmetrical fragments. A calculation of a Berny-type TS [HF/3-21G] yielded a chair-like structure with a characteristic imaginary vibration of -818.10 cm^-1 and a symmetry of C1. This vibration describes an approach of two terminal carbon atoms while the two other terminal atoms bend away from one another. This clearly represents the formation of one bond between two atoms on one side and the breaking of a bond on the other. The central carbon atom in both fragments approaches the bond-breaking carbon atom, establishing the reduced distance needed for the future double bond to form. Thereby the distance between the central and the bond forming atom is reduced to the level of a single bond. After one half cycle of the vibration, the structure relaxes again to its original state and continues the same movement on the other side of the molecule. While clearly a correct TS was found, the symmetry is not correct. Therefore, the TS was calculated again, symmetrising the guess to the highest level possible (C2v). This second calculation yielded a TS of C2 symmetry, which was caused by asymmetrical terminal C-C bonds. The frequency however is exactly -818.00 cm-1. Finally, this structure was resymmetrised to C2h, the bonds responsible for the asymmetric behaviour were frozen via redundant coordinates and the TS could be obtained after a further optimisation [HF/3-21G]. The final point group is C2h and the imaginary frequency is -818.04 cm^-1, E = -231.61932238 a.u..

The characteristic vibration of the Cope rearrangement chair-TS.

Secondly, the chair-like TS was optimised via a redundant coordinate approach, which avoided the need to compute an expensive Hessian matrix. The two allyl fragments were aligned in a boat-like fashion. In a first step, the terminal intermolecular C-C distances were freezed to 220 pm, in the second this bond length was optimised via a redundant coordinate calculation [both HF/3-21G]. This calculation resulted in a similar TS to before. The point group is again C2h, while the characteristic vibration has a frequency of -817.84 cm^-1. The two TSs calculated above exhibit largely similar features. The geometry is equivalent, the point group is the same. Small differences in the exact bond angles and bond lengths can be found. The difference between the two TSs' properties is too small to be revelant and is likely due to computational inaccuracies(E(Berny) = -231.61932238 a.u., E(Red. Coord.) = -231.61932232 a.u.; Bond length (Berny) = 138.924 pm, Bond length(Red. Coord.) = 138.929 pm). However, as a frozen coordinate step was employed in the step above, it is unwise to draw any comparisons about the two methods from these results.

By following the Intrinsic Reaction Coordinate (IRC) of the Berny TS its relevance may be estimated [HF/3-21G, Hessian always computed]. The calculation terminated successfully after 44 steps, having formed the structure "gauche2" of symmetry C2.

The IRC starting from the chair-TS.

The boat-like TS was obtained by another method. In the QST2 method, a reactant and a product are given as arguments to the program, which then linearly interpolates between them in order to locate a TS. This method required a great deal of attention, as atomic labels needed to be assigned with care - it was necessary to predict the movement of terminal hydrogen atoms with Woodward-Hoffmann rules (conrotary vs. disrotary). A number of consecutive calculations had to be conducted in order to locate the TS. The final structure shows C2v symmetry and a characteristic vibration of -839.98 cm^-1. The vibration itself is similar to the one observed for the chair-like TS, only that one of the allyl fragments is turned upside down.

The characteristic vibration of the Cope rearrangement boat-TS.

In order to establish the more favourable TS, their energies must be compared. Both TSs were reoptimised at a higher level of theory to increase the significance of the results [DFT/B3LYP/6-31G*]. The chair TS now shows lower intermolecular distances (2.02028 -> 1.96622 A), but higher intramolecular distances (138.924 -> 140.765 pm). The total energy was lowered substantially in the process (-231.61932238 a.u. -> -234.55692633 a.u.). Conversely, both bond lengths in the boat-like TS increased. As before, the total energy decreased significantly (-231.60280249 a.u. -> -234.54307872 a.u.). However, while the boat-like TS was lower in energy before the optimisation, it is now higher in energy than the chair-like TS. As an optimisation at a higher level of theory is more reliable, this indicates that the chair-like TS is more realistic. Conversely, this energy difference is not as big as expected. The sum of electronic and zero point energy was calculated as follows: Reactant = -234.469219 a.u., Chair = -234.414918 a.u., Boat = -234.402355 a.u.. This clearly shows that the activation energy for the chair TS is 0.054301 a.u. and that of the boat is 0.066864 a.u.. Therefore we see that the chair Ts is the more favourable TS.

Applying a conversion factor of 627.503 for the conversion of hartrees to kcal/mol, the activation energy of the chair TS is 34.07 kcal/mol and that of the boat 41.96 kcal/mol. This is within a 10% tolerance of the experimental values of 33.5 & 44.7 kcal/mol and shows therefore excellent agreement.

The Diels-Alder Cycloaddition

Firstly, a structure for cis-1, 3-butadiene was optimised from two ethene fragments [DFT/B3LYP/6-31G*]. It was necessary to freeze the main C-C-C-C dihedral angle to prevent any angular distortion. The so optimised structure is of planar geometry. The HOMO of this molecule is mostly influenced by the two pi-bonds. Clearly the positive overlap of the p-orbitals generates an electron cloud parallel to the corresponding sigma bond, allowing for electron donation. The orbital is antisymmetric with respect to a plane, as the two pi-bonds are out of phase with one another (the next lower orbital exhibits both pi-bonds in phase). The LUMO is dominated by the antibonding equivalent to the pi-bonds in the HOMO. The lobes are concentrated at the terminal atoms and around the central C-C single bond. The orbital is symmetric with respect to the plane.

The HOMO of cis-Butadiene. It is antisymmetric with respect to a mirror plane

The LUMO of cis-Butadiene, as seen from the top. Nodes can be found in the plane of the atoms. It is symmetric with respect to a mirror plane.

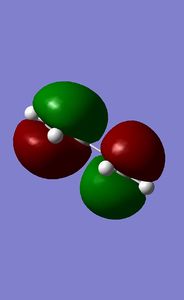
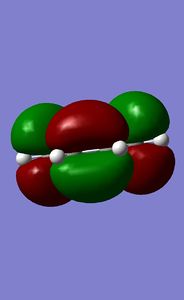
Combining this fragment with a simple ethene fragment in an envelope fashion leads to an approximation of the TS. Symmetrisation and subsequent optimisation to a Berny TS [Semi-empirical/PM6] result in a TS of energy 0.11286018 a.u. and symmetry Cs. The characteristic vibration has a frequency of -948.70 cm^-1 and clearly shows the expected movement.

The characteristic vibration of the TS in the Diels-Alder reaction to form cyclohexene.

The HOMO and LUMO of both reactants are shown. Linear combinations of orbital pairs with equivalent symmetry result in a simple frontier MO diagram of cyclohexene. Ethene approaches butadiene from the top, intersecting both double bonds (orbital overlap not indicated, due to reasons of display and overview). This intersection does not halve the pi bonds, but is rather biased towards the terminal end of the double bonds, which gives the TS its characteristic envelope shape. The combination of the butadiene HOMO and ethene LUMO yields the lowest energy MO. This MO is stabilised the most, as the butadiene pi-bonds overlap fully with one orbital of the ethene pi* orbital. A node in the ethene double bond is formed. It is followed by the HOMO, formed by overlap of the butadiene LUMO and the ethene HOMO. Here two nodes are formed in the butadiene double bonds, while the pi-orbitals of the central carbon atoms show a strong interaction, indicating the future double bond. This prediction is further confirmed by the computed HOMO for the TS. The HOMO is symmetric with respect to a plane. The LUMO is also symmetric, showing an overall similar geometry compared to the HOMO. However, the polarity of the butadiene MO is inverted, allowing for less overlap with ethene. This can again be seen in the computed MO. Finally, the highest energy orbital shows no overlap of ethene with butadiene, it is in fact closest to the orbital distribution of the reactants. This is expected, as the reaction is spontaneous and therefore the reactants are bound to be of higher energy than the product. Each reactant orbital can be related to a product orbital of the same symmetry with respect to a central mirror plane. The Woodward-Hoffmann rules state that a ground state pericyclic reaction is symmetry allowed if the sum of all 4n+2 suprafacial and all 4n antarafacial components is odd. As this reaction has 6 electrons participating in solely suprafacial geometries, this reaction is symmetry allowed.

The HOMO and LUMO orbitals for both butadiene and ethene are shown in the top right corner. A simplified MO diagram considering only these 4 orbitals is drawn to the right. The frontier orbitals of the TS are shown to the bottom left.

The calculated HOMO of Cyclohexene.

The calculated LUMO of Cyclohexene.

The reaction scheme for the Diels-Alder reaction of cyclohexadiene and maleic anhydride.

The reaction scheme for the Diels-Alder reaction of cyclohexadiene and maleic anhydride.

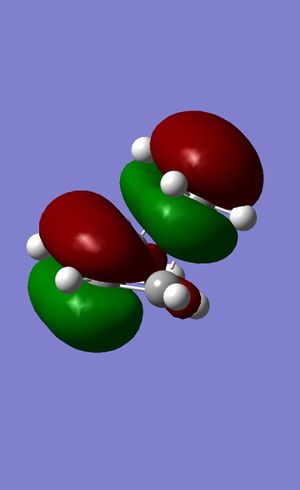
The more complex reaction set out above proceeds via two TSs, one for each product. Essentially the two products differ in the orientation of the maleic anhydride fragment towards the diene, being either aligned close to it (endo) or pointing away from it (exo). These TSs were located by first optimising a maleic anhydride structure at a high level of theory [DFT/B3LYP/6-31G*] and then docking this fragment onto a cyclohexene fragment. By aligning the anhydride fragment at different angles and distances, the two TSs could be obtained via multiple resymmetrisations and reoptimisations [Semi-empirical/AM1]. Both results show imaginary vibrations corresponding to the expected motions (endo = -790.62 cm^-1; exo = -218.13 cm^-1.The vibrational modes are depicted below. It can clearly be seen that the two fragments approach one another, forming a bond, while the former double bond forming carbon atoms dissociate ever so slightly. Lastly, the two carbon atoms forming the new double bond move closer together, which indicates that this transition state is closely related to the reaction being investigated.

The differences between the two conformations are minimal at a first glance. However, as only the TS for both can be seen, it should be noted that the hybridisation of the carbon atoms close to the anhydride fragment differs. In the exo structure, the carbons are sp³ hybridised, while the corresponding atoms in the endo structure are only sp² hybridised. This leads to additional steric crowding and strain via hydrogen atoms pointing directly at the anhydride fragment. In the endo structure, the C-C distance between this crowding CH2-CH2 fragment is as large as 379.503 pm, whereas the one in the exo structure is 321.827. More importantly, the next hydrogen is just 277.686 pm away. This will contribute to steric strain.

The characteristic vibration of an endo TS in the Diels-Alder reaction.

The characteristic vibration of an exo TS in the Diels-Alder reaction.

A diagram of bond lengths in the endo TS.

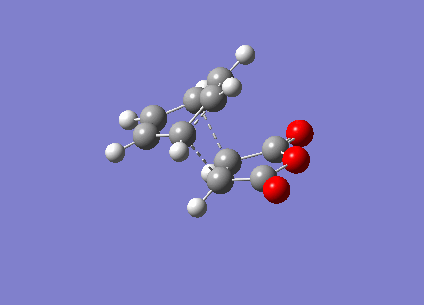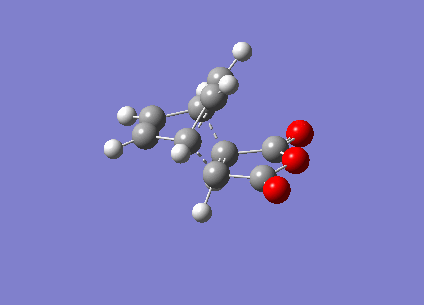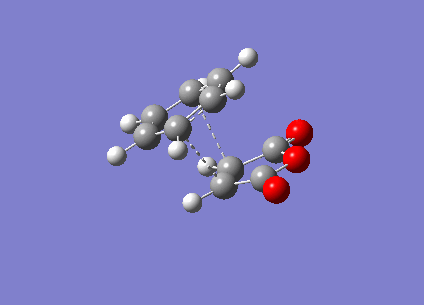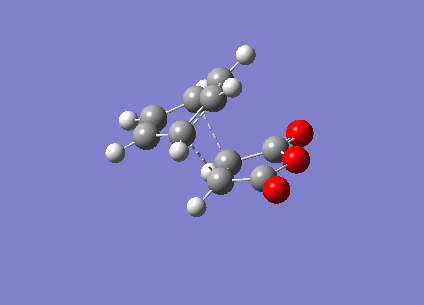
It can be seen that the TS exhibits intermediate bond lengths. All single bond lengths are slightly lowered below their usual value, while those of double bonds are slightly increased. Especially interesting is the single bond length in the cyclohexadiene ring, which shrunk to double-bond level, indicating the double bond forming between these two atoms. Overall this is an index for the increased amount of delocalisation in the aromatic TS. Finally, comparing the relative energies of the two conformations (endo = -0.02802515 a.u., exo = -0.02149015 a.u.). The activation energies of the two states are endo = 380716 kcal/mol & exo = 380734 kcal/mol. It is evident that the endo TS is slightly more favourable, even though this difference might be due to computational inaccuracy.

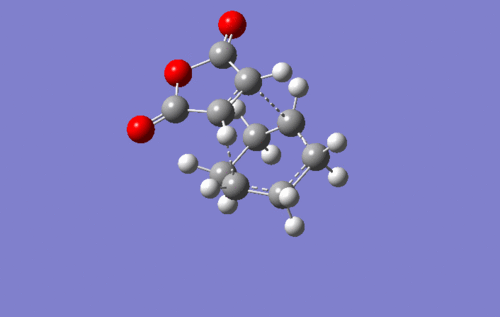
I small hint on the secondary orbital stabilisation effective in the endo TS could be found as well. The picture below depicts the HOMO of the endo TS. The green lobe of the cyclohexadiene ring may overlap with the antibonding lobes located on the oxygen atoms. This possible interaction is completely absent in the exo TS. In fact, this HOMO has a completely different shape to that of the endo state.

The HOMO of the endo TS.

The HOMO of the exo TS.

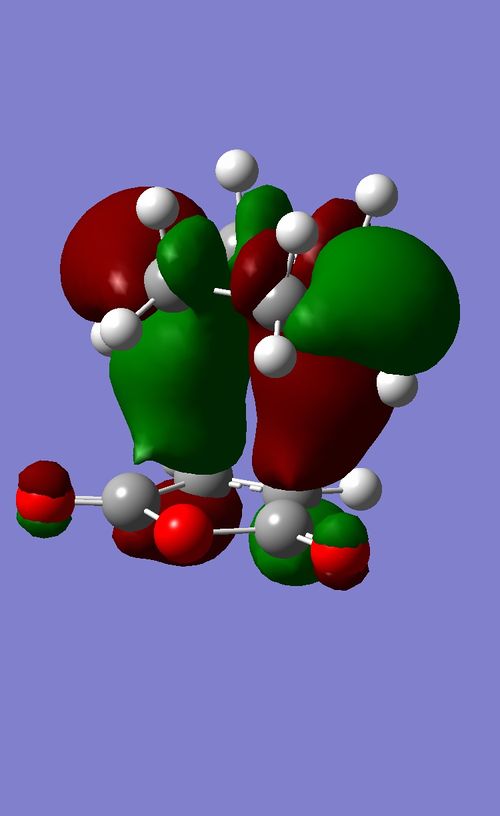
Conclusion

A range of transition states for a number of pericyclic reactions were located. Investigation of imaginary frequencies allowed for the estimation of the quality of said TSs. It was shown that the Cope rearrangement may pass through one of two transition states, of which the chair geometry is more favourable by about 10 kcal/mol. The obtained values were within 10% of experimental data. Their geometries and symmetries were determined and IRC calculations showcased their function as bottlenecks in the reaction pathway. Two Diels-Alder reactions were interpreted from a quantum chemical point of view. The selection rules and symmetry requirements for pericyclic reactions were met by the found TSs. Moreover, a possible orbital interaction explaining the endo effect was discovered.

This experiment provided insight into the calculation of Transition States and the origin of the orbitals that chemists work with everyday. In doing so, it certainly raised more questions than it could answer. As points of further discussion, all transition states should be subjected to IRC analysis to establish that they are real transition states. Furthermore, guess structures for future optimisations should be carefully assembled based on orbital symmetry considerations of the reactants. Only then can reliable TS structures be found. Moreover, the guessing of initial structures may be automated by a computer script to increase the efficiency of searching, as a range of initial conditions could be scanned conveniently.