Rep:Mod:bc608 module1

Module 1: Modelling with Molecular Mechanics

---

Introductory remarks

Throughout this report, total energies of molecules are separated into various components. These additive, non-interacting terms are defined below:

Stretch: The sum of all diatomic bond stretches, as calculated by a Hookes law potential.

Bend: The sum of all triatomic bond angle deformations, also calculated by a Hookes law potential.

Stretch-Bend: A correction to account for the coupling between stretching and bending.

Torsion: The sum of all tetra-atomic bond torsions, modelled by a cosine dependance upon angle.

Van der Waals: The sum of all Van der Waals repulsions using a Lennard-Jones potential.

Dipole-dipole: The sum of all electrostatic attractions of individual bond dipoles.

Energies throughout are reported in kcal mol^-1 in keeping with computational conventions. The energies are effectively "meaningless", as in they cannot be measured experimentally. It is only the relative differences between energies which is meaningful, so energies are left in kcal mol^-1.

Unless otherwise stated, all energies are reported to 2 decimal places. The calculation techniques use numerical methods to minimise the energy of a system. The system is deemed to be optimised when the system energy/iteration gradient falls below a set value (fixed as 0.01 in these calculations).

All calculations were performed using ChemBio3D program version 12.0. Program bugs have been identified where possible.

The Hydrogenation of the Cyclopentadiene Dimer

Endo/Exo selectivity in the dimerisation of cyclopentadiene

Cyclopentadiene is a versatile reagent and has found a wide range of applications in chemistry. The anionic form of cyclopentadiene C₅H₅^- (more commonly known as "Cp") is heavily utilised in organometallic chemistry and catalyst design as a complexing ligand capable of varying its hapticity. One such industrial application of the Cp ligand is Ziegler-Natta type catalysis of alkene polymerisation. Cyclopentadiene can also be used to generate norbornene systems via Diels-Alder 4π_S + 2π_S cycloaddition reactions. One such, often unwanted reaction is the dimerisation of cyclopentadiene, which results from the 4π_S + 2π_S cycloaddition of two cyclopentadienes.

Two diastereoisomers can form - the exo isomer (1) and the endo isomer (2).

Structure 1: The exo-dimer of cyclopentadiene		Structure 2: The endo-dimer of cyclopentadiene

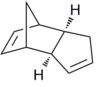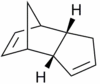Baldwin has reported that cyclopentadiene dimerises to form the endo isomer (2) preferentially. It was also shown that the endo isomer (2) can be converted to the exo isomer (1) at higher temperatures. In order to investigate this phenomena, Allinger's MM2 force field was utilised to optimise the geometry of each diastereoisomer, such that a minimum energy conformation is adopted for each diastereoisomer. The results are shown below.

	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Exo dimer (1)	1.29	20.60	-0.84	7.65	2.80	0.38	31.88
Endo dimer (2)	1.25	20.87	-0.83	9.50	2.78	0.45	34.01

Figure 1: A table to compare the energies of the exo and endo dimers

Figure 2: The source of 1,4 strain in the endo dimer is shown with a red arrow between 2 carbons in the norbornene ring and 2 carbons in the cyclopentene ring.

It can be seen that the exo isomer (1) is thermodynamically more stable than the endo isomer (2) by 2.13 kcal mol^-1. The major component of this 2.13 kcal mol^-1 destabilisation energy of the endo isomer relative to the exo isomer is the result of tetra-atomic bond torsion contributions i.e. repulsion between atoms located in a 1,4 relationship (9.50 cf. 7.65, endo cf. exo). When the structures of the isomers are compared, one can see a significant source of 1,4 strain in the endo isomer between carbons that is not present in the exo isomer. This 1,4 strain is illustrated in Figure 2. It is important to note that there are two such interactions due to the symmetry of the molecule.

Despite the endo isomer (2) being thermodynamically less stable, it is formed preferentially. In order to understand this observation, we must first consider what happens during a reaction where two possible products may form.

The product with the lowest energy transition state barrier of formation will always be initially formed preferentially due to the faster rate of reaction. The final product distribution however will be determined by the reversibility of the reaction, which is often condition dependent, giving rise to two types of control.

• Kinetic control - Under kinetic conditions, there is a small amount of thermal energy in the reaction mixture and thus the reaction is effectively irreversible. Starting materials are brought together and react to give a product mixture dependent upon the rates of the competing processes. Once products have formed, they cannot undergo a reverse reaction to reform reactants. The kinetic product is therefore the product with the lowest energy transition state barrier.
• Thermodynamic control - Under thermodynamic conditions, the kinetic product is still initially formed preferentially. However, there is sufficient energy in the system present to convert the kinetic product to starting materials. Kinetic product will therefore be continuously converted to starting material. The thermodynamic product acts as an energy sink, thus, over time, it will dominate the product distribution.

It is important to note that the "thermodynamic" and the "kinetic" product may in fact be the same product, in which case this product will be the major product under all conditions.

Applying this to our case, the exo isomer has already been shown above to be thermodynamically more stable. If the exo isomer also had a lower energy transition state barrier of formation, then it would be formed under thermodynamic and kinetic conditions. However, this does not agree with Baldwin's observations in which he found the endo isomer to be formed preferentially under kinetic conditions and the endo isomer to convert to the exo isomer at higher temperatures. Therefore, it must be the case that the endo product has a lower energy transition state barrier of formation, otherwise it would not be the major product under any conditions.

Now that the transition state for the formation of the endo isomer has been shown to be lower in energy than the transition state for the formation of the exo isomer, it is important to understand why this is the case.

Figure 3: The transition state for the formation of the endo isomer of the cyclopentadiene dimer. Dotted lines show the location of the sigma bonds to be formed. In the right hand image, the orbitals involved in bonding have been omitted in order to examine the overlap of other orbitals in the transition state.		Figure 4: The transition state for the formation of the exo isomer of the cyclopentadiene dimer. Dotted lines show the location of the sigma bonds to be formed.

By the consideration of frontier molecular orbitals (Figure 3) it can be seen that the endo transition state experiences stabilisation, due to additional favourable orbital overlap between the HOMO (top) and LUMO (bottom) at the back of the molecule. It can be seen that in the case of the exo transition state (Figure 4) this additional HOMO/LUMO overlap at the back of the molecule does not exist and therefore the energy of the transition state is higher.

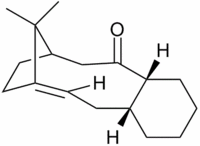
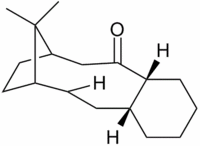
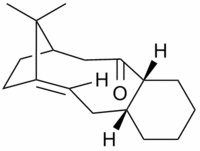
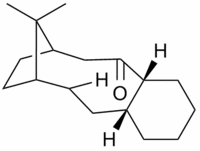
Hydrogenation of the endo isomer of the cyclopentadiene dimer

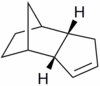
Hydrogenation of the endo cyclopentadiene dimer initially proceeds to give a dihydro derivative and only forms the tetrahydro derivative after prolonged hydrogenation. There are two alkenes in the endo cyclopentadiene dimer and thus a question of regioselectivity arises: Initially, is structure (3) or (4) formed?

The structures of 3 and 4 were minimised using the MM2 force field, in order to elucidate why one structure is formed preferentially over the other and whether the hydrogenation is under thermodynamic or kinetic control.

Structure 3: A possible mono-hydrogenation product of the endo-dimer of cyclopentadiene	Structure 4: A possible mono-hydrogenation product of the endo-dimer of cyclopentadiene

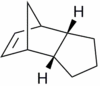	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Total
Structure 3	1.28	19.80	-0.84	10.87	4.42	0.16	35.70
Structure 4	1.10	14.50	-0.55	12.51	3.46	0.14	31.16

Figure 5: A table to compare the energies of the dihydro hydrogenation products

As can be seen from Figure 5, structure 4 is more stable than structure 3 by 4.54 kcal mol^-1. The main component of this difference can be seen to be due to angular strain (bend component).

Figure 6: The angle θ

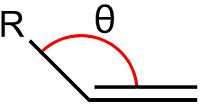
The angle θ between a double bond and a substituent of the alkene is shown in Figure 6. In structure 3 this angle is measured to be 107.81°. In structure 4 this angle is measured to be 112.40°. The carbons in alkenes are SP² hybridised and so have ideal bond angles of 120°. Deviation from this ideal angle will lead to angular strain, thus it is clear that structure 3 will be experience more angular strain than structure 4 due to its larger deviation from the ideal bond angle. And therefore, structure 4 is the most stable product.

Experimentally, it is indeed seen that structure 4 forms preferentially. However, it is important to note that it cannot be determined whether the hydrogenation reaction is under kinetic or thermodynamic control. Whilst structure 4 is thermodynamically more stable than structure 3, the energy of the transition state barrier to formation is completely unknown and cannot be inferred from experimental observations as previously. It is entirely possible that structure 4 also has a lower transition state barrier of formation than structure 3 and so would also be the major product under kinetic conditions.

Modelling of the transition state would be required in order to determine if the hydrogenation reaction is under thermodynamic or kinetic control. This cannot be achieved with Molecular Mechanics and requires consideration of the orbitals involved.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

The reaction between a prolinol derivative and methyl magnesium iodide

Figure 1: Reaction Scheme for the reaction between a prolinol derivative and methyl magnesium.

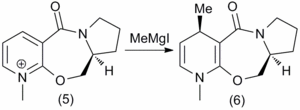
It is found experimentally that the reaction between a prolinol derivative(5) and methyl magnesium iodide proceeds regio- and enantioselectively. This may initially be somewhat surprising as one could envisage attack at the 2 and 6 positions of the pyridine ring being equally probable. In fact, the reaction with Methyl Lithium shows a poor regioselectivity and a 50:50 mixture of regioisomers. The reaction is shown in Figure 1.

The starting material, prolinol derivative (5) was modelled using MM2 in order to try and rationalise the observed regio- and stereoselectivity of the reaction with the Grignard reagent.

Of the 5 and 7 membered rings, it was decided that the 5 membered ring was the more conformationally flexible. A large portion of the 7 membered ring is planar due to the planarity of atoms directly bonded to the phenyl ring and the planarity of amide bonds. The stereochemistry of the bridgehead of the 7 and 5 membered rings further increases the inflexibility of the 7 membered ring. As the 5 membered ring possesses the most conformational flexibility, it seemed prudent to optimise this ring structure first and then consider the 7 membered ring afterwards if it needs adjustment.

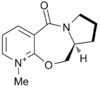
5 membered rings adopt envelope conformations preferentially. With reference to Figure 2 it can be seen that there are two possible conformations for prolinol derivative (5), C_V may be "up" (5A) or "down" (5B).

Structure 5A: The structure of the prolinol derivative optimised with MM2 where Cv is up	Structure 5B: The structure of the prolinol derivative optimised with MM2 where Cv is down	Figure 2: The structure of the prolinol derivative (5) illustrating the varying carbon in the 5 membered ring - denoted CV.

The MM2 energies of the two structures are shown in Figure 3.

Structure	Energies /kcalmol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Charge-Dipole	Dipole-Dipole	Total
5A (up)	1.8256	14.2679	0.1517	6.62644	16.1906	1.7991	-3.9344	36.5648
5B (down)	1.8113	14.3592	0.1163	5.0995	16.0297	1.6843	-3.9874	35.1130

Figure 3: A table to show the energies of the two possible conformations of the 5 membered ring within the prolinol derivative (5)

These MM2 calculations show that 5B, with a "down" C_V carbon gives a more stable structure.

It was then realised that the conformation of the 7 membered ring is completely fixed after the geometry of the 5 membered ring had been altered, thus the 7 membered ring could not be optimised further. Therefore structure (5B) represents the structure of the prolinol derivative (5).

The dihedral angle between the aromatic ring and the carbonyl group was examined. For clarity, this dihedral angle is illustrated in Figure 4.

Figure 4: The dihedral angle between the aromatic ring and the carbonyl group is shown in bold

This angle was measured to be +10.9034° i.e. the carbonyl points forwards and lies above the plane of the pyridine ring. This can be seen visually in the Jmol of (5B) above. In order to see if there were any other stable carbonyl geometries, the dihedral angle between the carbonyl group and the aromatic ring was varied in increments of 2° and for each dihedral angle the geometry optimised with MM2 whilst holding the dihedral angle constant. The calculated total energies were then plotted. The results can be seen in Figure 5.

Figure 5: The variance of calculated energy with dihedral angle between the carbonyl and aromatic ring

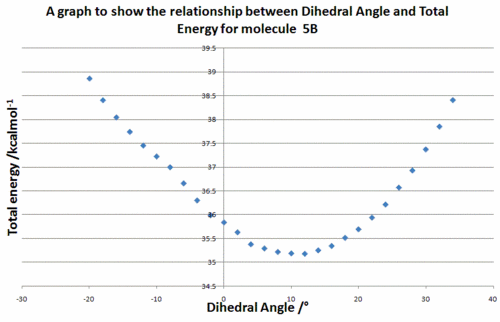
At this point, it is important to note that the ChemBio3D program version 12.0 used in these calculations contains a bug which affects the molecular mechanics force field when applied to molecules containing N⁺ atom types. It has been reported that this bug impacts upon the eventual energy and geometry obtained using the mechanics method. As the molecular mechanics methods are bugged, the calculation was run using another molecular mechanics force field, MMFF94, to see if the bug also applied to this force field. The geometry optimisation was also performed using MOPAC/PM6, a molecular orbital method, to provide an unaffected reference point. The results can be seen in Figure 6.

Structure
	Total Energy using MMFF94 /kcalmol-1	Heat of formation using MOPAC/PM6 /kcalmol-1
5A (up)	59.0238	93.68831
5B (down)	57.4784	93.90012

Figure 6: A table to show the calculated energies of the structures. Note: A higher heat of formation means its formation is more exothermic i.e. it is more stable and of lower energy.

Fortunately, whilst molecular mechanics methods in ChemBio3D version 12 do suffer from a bug with N⁺ type atoms, 5B is still more stable for all calculation methods. The dihedral angles were measured under the different optimised methods and the results are shown in Figure 7.

Calculation
	Dihedral Angle (O=C-C-C) /degrees
MM2	+ 10.9034
MMFF94	+ 17.6672
MOPAC/PM6	+ 25.6193

Figure 7: A table to show the calculated dihedral angles between the carbonyl and aromatic ring for different calculation methods

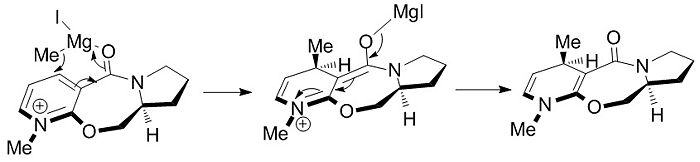
Despite the differences in absolute values of angle, in all cases the value is positive in magnitude and thus lies above the plane of the pyridine ring. The cause of the stereo- and regioselectivity can now be elucidated. The magnesium atom in a Grignard reagent is electron deficient and has vacant orbitals i.e. it is Lewis acidic. Amides are Lewis basic and thus a Lewis acid/base interaction will exist between the reactants. In other words, the oxygen of the carbonyl complexes to the magnesium of the Grignard reagent. As the carbonyl sits above the plane of the pyridine ring, the methyl nucleophile will also be directed to the top face of the ring resulting in the stereochemistry seen in the reaction scheme in Figure 1. In the case of methyl lithium, the organometallic reagent is much more reactive than in the case of the Grignard reagent, due the increased electropositivity of the metal species. The mechanism for the MeLi attack will not involve prior complexation of the carbonyl to the organometallic reagent, resulting in a statistical mixture of regioisomers.

A proposed mechanism is shown in Figure 8.

Structure 5C: The structure of Prolinol optimised with MMFF94 where Cv is down

Structure 5D: The structure of Prolinol optimised with MOPAC/PM6 where Cv is down	Figure 8: The mechanism of the methylation at the 4 position

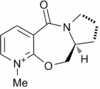
Phenylamine attack on a quinoline ring

Figure 1: Reaction scheme for the reaction between phenylamine and a quinoline ring(7)

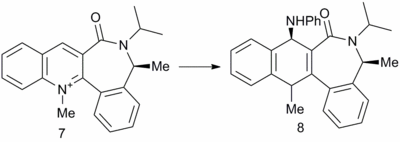
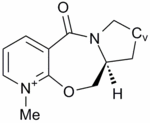
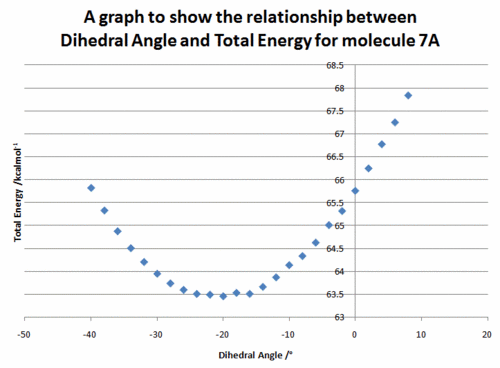
The above reaction was found to proceed stereoselectively as shown. In this example there is no issue of regioselectivity, as there is only one position for attack of the incoming nucleophile. The conformation of the 7 membered ring was again relatively inflexible, due to the large number of planar components around the ring and only two conformations were found. One conformation resulted in the carbonyl above the plane of the quinoline ring (7A), the other conformation resulted in the carbonyl below the plane of the ring (7B). The energies were calculated to be 63.50 kcal mol^-1 and 66.48 kcal mol^-1 respectively.

Structure 7A: The structure 7 with the carbonyl below the plane of the quinoline ring optimised with MM2	Structure 7B: The structure of 7 with the carbonyl above the plane of the quinoline ring optimised with MM2	Structure 7A: The structure of 7 optimised with MMFF94	Structure 7A: The structure of 7 optimised with MOPAC/PM6	Figure 2: A graph to show the variation of total energy as dihedral angle is altered

The effect of dihedral angle between the carbonyl group and the aromatic ring upon total energy as calculated by MM2 was again examined. The results are shown in Figure 2.

Calculation
	Dihedral Angle/°
MM2	-20.1657
MMFF94	-33.6555
MOPAC/PM6	-43.5024

Figure 3: A table showing the calculated dihedral angles between the carbonyl and the quinoline ring

Figure 2 shows that only negative values of the dihedral angle give a total energy minima, placing the carbonyl on the bottom face of the molecule. In the previous example, an electropositive atom on the incoming nucleophile complexed to the carbonyl oxygen prior to the nucleophilic attack in order to direct the nucleophile to the same face as the carbonyl. In this example, prior complexation of the nucleophile to the carbonyl is not possible. Instead, the nucleophile contains a lone pair of electrons on the nitrogen atom. The carbonyl atom also contains lone pairs. When lone pairs are brought together they experience electrostatic repulsion as shown by Coloumb's law. The phenylamine will therefore avoid the bottom face of the molecule to avoid electrostatic repulsion and so the amine will occur preferentially from the top face to give 8. The mechanism is shown in Figure 3.

Figure 3: The mechanism of the nucleophilic attack at the 4 position

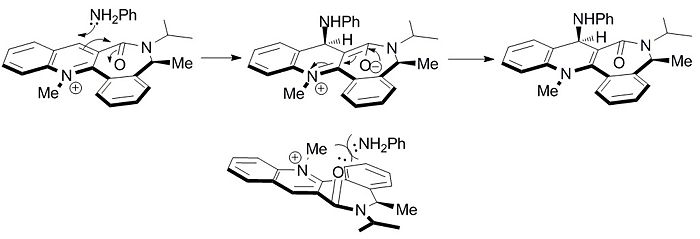
Using what has been learnt from the previous two exercises, one can predict the reactions of both 5 and 7 with phenylamine and MeMgI. One would expect the reaction between 7 and MeMgI to give a "down" stereochemistry of the methyl group due to the prior complexation of the carbonyl oxygen to the magnesium atom. One would also expect the reaction between 5 and PhNH₂ to give a mixture of regioisomers, with substitution at the 2 and 4 positions seen. For substitution at the 4 position, one would expect a down stereochemistry of the PhNH substituent. For 2 substitution, one would expect a mixture of stereoisomers.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

A key intermediate in the total synthesis of Taxol is initially synthesised with the carbonyl group pointing either up (9) or down (10). On standing, the compound isomerises to the alternative carbonyl isomer. This implies that a kinetic product was initially formed in the formation reaction of the key intermediate, which upon standing is being converted to the thermodynamic product. By examining the energies of the possible isomers, the identity of the kinetic and thermodynamic isomers can be established.

Figure 1: The structures 9 and 10

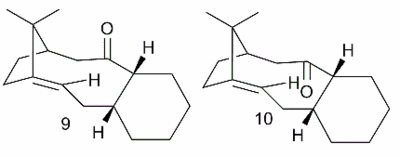
The cyclohexyl ring was recognised as having 2 possible conformations - the preferred chair or the energetically expensive twist boat. Only one chair and one twist boat structure were found for structure 9. The results of MM2 and MMFF94 force field minimisation are shown in Figure 2.

	Total Energy
	MM2/ kcal mol-1	MMFF94/ kcal mol-1
Intermediate 9A (Chair)	48.8839	70.5483
Intermediate 9B (Twist boat)	54.3499	76.3053
Intermediate 10A (Chair front C-C down)	44.3057	60.5683
Intermediate 10B (Chair front C-C up)	53.0718	74.845
Intermediate 10C (Twist boat)	48.1702	66.3484

Figure 2: A table to show the energies of the conformers of 9 and 10

It was seen that MMFF94 and MM2 give the same trends in energies for the conformers of 9 and 10. However, it is important to note that the energies cannot be compared directly e.g. "For 9A chair, MM2 and MMFF94 disagree by around 21 kcal mol^-1. The two methods use different parameters and approaches to calculating the non-interacting terms described in the introductory remarks. Interestingly, two chair conformers were found for intermediate 10, of which 10A was the lowest energy conformation. Therefore, it is likely that structure 9 is formed initially in the reaction and upon standing, it converts to structure 10.

Structure 9A: A possible intermediate in the synthesis of taxol with the cyclohexyl ring in a chair conformation	Structure 9B: A possible intermediate in the synthesis of taxol with the cyclohexyl ring in a twist-boat conformation	Structure 9C: The hydrogenation product of 9A

Structure 10A: A possible intermediate in the synthesis of taxol with the cyclohexyl ring in a chair conformation with the front carbon-carbon bond at the bridge bead pointing down	Structure 10B: A possible intermediate in the synthesis of taxol with the cyclohexyl ring in a chair conformation with the front carbon-carbon bond at the bridge bead pointing up	Structure 10C: A possible intermediate in the synthesis of taxol with the cyclohexyl ring in a twist-boat conformation	Structure 10D: The hydrogenation product of 10A

In order to understand why the alkenes of 9 and 10 react slowly, the energy contributions to the total energy were examined for 9A and 10A with the corresponding alkanes. The most common reactions of alkenes are electrophilic addition reactions, which involve a change of hybridisation from sp² to sp³ and thus comparing the alkene to the alkane seems a reasonable model for the further subsequent functionalisation of the molecule. The results are shown in Figure 3

Structure	Energies/ kcal mol-1
	Stretch	Bend	Stretch-Bend	Torsion	Van der Waals	Dipole-Dipole	Total
9A (chair)	2.67	15.91	0.40	18.23	11.54	0.15	48.88
9C (chair, alkane)	2.66	15.63	0.58	23.43	14.37	0.00	56.67
10A (chair front R down)	2.56	10.72	0.33	19.57	11.31	-0.18	44.31
10D (chair, alkane)	2.83	13.43	0.65	22.05	14.17	0.00	53.13

Figure 3: A table to compare the energies of the alkenes 9 and 10and the alkane derivatives of the structures

It can be seen that 9 and 10 are more stable than their corresponding alkanes. They are therefore classed hyperstable alkenes. Hyperstable alkenes are alkenes that have negative olefin strain energies, where:

Olefin Strain Energy = Total energy of alkene - total energy of alkane

The olefin strain energies for 9 and 10 are calculated to be -7.79 kcal mol^-1 and -8.83 kcal mol^-1. The main components of these olefin strain energies can be seen to be from Torsion and Van der Waals contributions. These two contributions are examined with respect to molecule 9.

Figure 4: The bond angle between Carbons A, B and C is responsible for the increased torsion component of energy between alkane and alkene

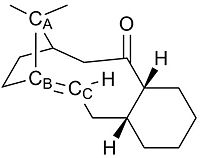
The angle between carbons A,B and C is measured to be 124 for the alkene and 119 for the alkane. Alkenes are sp² hybridised and have ideal bond angles of 120. Alkanes are sp³ hybridised and have an ideal bond angle of 109.5. The alkane shows the largest deviation from the ideal bond angle and so experiences significantly more torsional strain. This increase in torsional strain disfavours the C_C centre from becoming sp³ hybridised and thus the alkene shows slow reactivity with electrophilic reagents.

The other major contribution to the olefin strain energy was seen to be due to Van der Waals interactions. Van der Waals interactions are calculated using a Lennard Jones 6-12 potential, shown in Figure 5.

Figure 5: The 6-12 potential used to describe Van der Waals forces in the MM2 optimisation compared to emperical measurements

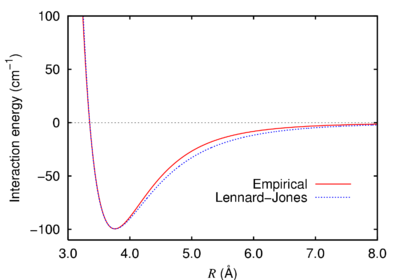
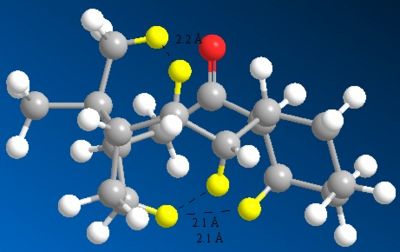
It can be seen that at short distances the function is strongly repulsive. For H-H interactions, the function is repulsive at around 2.1Å and attractive at around 2.4Å. The close contacts between atoms in the alkane structure were calculated and a number of repulsive H-H Van der Waals interactions were found. The alkene structure also showed one less repulsive Van der Waals interaction. These repulsive H-H Van der Waals interactions are shown in Figure 6 and Figure 7.

Figure 6: The repulsive Van der Waals interactions present in the alkane

Figure 7: The repulsive Van der Waals interactions present in the alkene

Comparing the two images, it is now apparent that torsion is not the only reason for the hyperstability of alkene 9, there is also a transannular strain component. By going from alkene to alkane, one introduces an additional repulsive transannular H-H contact, raising the energy of the alkane relative to the alkene.

The slow reactivity of the alkenes 9 and 10 has therefore been rationalised. As the C_C carbon goes from sp² to sp³ hybridised, the molecule experiences increased angular and transannular strain. Forcing conditions will therefore be required to make the alkenes react, as the system is trying to go 'uphill' in energy.

Regioselective Addition of Dichlorocarbene

Orbital Control

Chlorocarbenes are very reactive electrophilic reagents due to their electron deficient nature. They react with alkenes via a formal cycloaddition mechanism to form cyclopropanes. It is seen experimentally that dichlorocarbene reacts regioselectively with 12 as shown in Figure 1.

Figure 1: The reaction between dichlorocarbene and 12

In previous sections, it was seen that molecular mechanics cannot handle molecular orbitals or transition states. In order to understand the the experimentally observed regioselectivity, a molecular orbital approach can be employed.

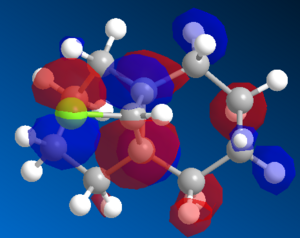
12 was preoptimised with MM2, then optimised and molecular orbitals calculated with MOPAC using the PM6 method. It was noticed that the HOMO was not symmetrical, which is aphysical. This calculated orbital is shown in Figure 2

Figure 2: Left: The HOMO calculated by PM6 Right: The C2 axis in structure 12

It can be seen that the PM6 method is giving non symmetrical orbitals, despite the C_S symmetry in the molecule. As the molecule is C_S symmetric, the orbitals should show C_S symmetry. It is likely that there is a bug within the PM6 method, therefore the calculations were repeated with the RM1 method.

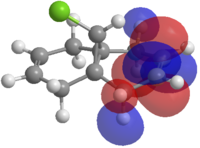
The HOMO-1, the LUMO, LUMO+1 and LUMO+2 were examined and are shown in Figure 3.

HOMO - 1

HOMO

LUMO

LUMO + 1

LUMO + 2

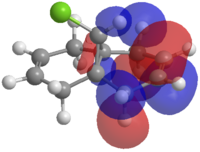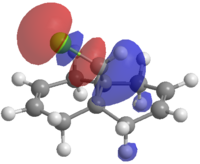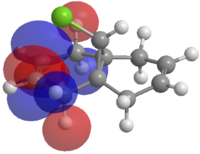Figure 3: The frontier molecular orbitals of structure 12.

The cause of regioselectivity is now evident. The HOMO of the molecule lies on the alkene endo to the C-Cl bond. One might envisage the two π orbitals to be of similar energy and therefore approximately equally nucleophilic. However, this is not seen experimentally. The π orbital exo to the C-Cl bond is capable of orbital overlap with the σ* orbital of the C-Cl bond. This results in the molecular orbital splitting diagram shown below.

Figure 4: A molecular orbital diagram to show the origin of the 5 discussed frontier orbitals

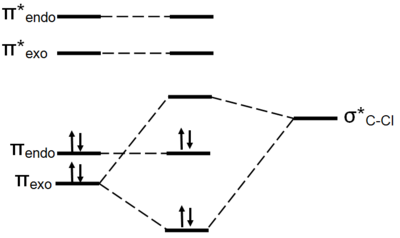
This stabilisation of the exo π orbital is possible due to the orbitals being in the correct orientation to interact and the orbitals being of similar energy. The π_C-C is a high lying filled orbital and the σ*_C-Cl orbital is a low lying empty orbital, due to the electronegativity of chlorine. This makes the exo π orbital more energetically stable and thus less nucleophilic. Nucleophilic attack therefore occurs from the endo π orbital.

Vibrational Energies

In order to test the previous analysis, the vibrational stretching energies for structures 12 were computed using MOPAC/RM1. These were compared to the stretching energies of 13, which is shown in Figure 1.

Figure 1: Structure 13

Bond	Structure 12			Structure 13
	Calculated Bond Length/Å	Wavenumber of stretch/cm-1	Vibration	Calculated Bond Length/Å	Wavenumber of stretch /cm-1	Vibration
C-Cl	1.782	770.86		1.791	780.03
C=Cendo	1.329	1757.34		1.329	1753.72
C=Cexo	1.331	1737.03		N/A	N/A	N/A

Figure 2: A table to compare stretching frequencies and bond lengths in 12 with 13

This is in agreement with the previously established argument.

For structure 13 only one C=C stretch due to the single double bond endo to the C-Cl. This C=C is unable to overlap with the C-Cl σ* and so these energies can be considered the "natural energies" with no secondary orbital overlap effects.

The IR of structure 12 is best understood by comparing the stretching energies to structure 13. The C-Cl stretch occurs at lower stretching energies (770.86 cf. 780.03) due to donation into the σ* of the C-Cl bond from the exo π orbital. The endo C=C stretching energy is comparable in magnitude (1757.34 cf. 1753.72) to the C=C stretching energy in 13, supporting the MO diagram drawn in the preceding section. The exo C=C stretching energy in 12 is lower than the C=C stretching energy in 13 (1737.03 cf. 1753.72) as a result of donation of π electron density into the σ* C-Cl bond. This imparts a more delocalised and diffuse orbital character between the two carbons resulting in a weaker bond.

The endo C=C bond is more nucleophilic because its π orbital it is more localised and higher in energy than the exo C=C bond π orbital. The difference in energies and localisation is due to orbital overlap of the exo C=C π orbital with the σ* C-Cl orbital.

Mini Project: The ring opening of epoxides by carboxylic acid enediolates

Functional group transformations of epoxides rank among the most fundamental reactions in Organic Chemistry. They are frequently used as key intermediates in total syntheses and are commonplace in natural products. Their versatility allows them to play a key biological role in a number of biosynthetic pathways; for instance Squalene 2,3-epoxide is a key biological precursor of cholesterol, steroid hormones and vitamin D.

The opening of styrene oxide with enediolates of carboxylic acids was found to give a mixture of isomeric products. The reaction scheme is shown in Figure 1.

Figure 1: Additions of dienediolates of carboxylic acids to styrene oxide.

The reaction shows regioselectivity - the epoxide can be opened at the most hindered position to give 3,4 substituted products or at the least hindered end to give 3,5 substituted products. The minor 3,4 regioisomer is produced in complete diastereoselectivity, whereas the major regioisomer is produced as a diastereotopic mixture. The mechanism for the formation of both regioisomers is shown in Figure 2 and Figure 3.

Figure 2: The proposed mechanism for the formation of (3R,4S)-3,4-diphenyl-3H-dihydro-2-furanone.

Figure 3: The proposed mechanism for the formation of racemic 3,5-diphenyl-3H-dihydro-2-furanone.

Assignment of regioisomers using ¹³C NMR

The two regioisomers, 3,4 and 3,5 substituted products can be separated by column chromatography and identified by ¹³C NMR.

The geometries of 1,2 and 3 were optimised using Density-Functional Theory at the MPW1PW91 level of theory and a 6-31G(d,p) basis set. The ¹³C NMRs of the optimised structures were then calculated using the GIAO method. The results are shown in Figure 3, with the carbon numbering system shown in Figure 2. The files are shown in Figure 4.

Figure 2: The referencing system used in the ¹³C assignments

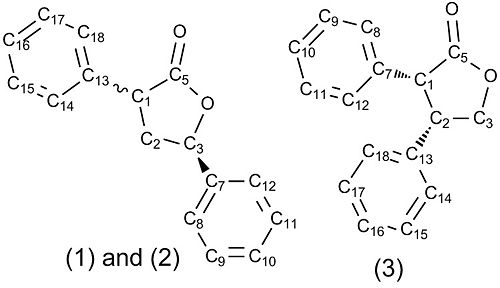
13C Chemical Shifts /ppm
(3R,4S)-3,4-Diphenyl-3H-dihydro-2-furanone			(3R,5S)-3,5-Diphenyl-3H-dihydro-2-furanone			(3R,5R)-3,5-Diphenyl-3H-dihydro-2-furanone
Literature	Calculated	Assignment	Literature	Calculated	Assignment	Literature	Calculated	Assignment
176.2	175.8*	C5	176.4	176.9*	C5	177.0	176.8*	C5
136.7	136.1	C13	138.7	139.7	C7	139.4	137.7	C7
133.0	131.0	C7	136.1	132.6	C13	136.5	134.6	C13
129.4	126.5	C12	129.1	126.1	C14	129.1	126.4	C14
128.9	126.5	C8	128.9	125.4	C9	128.9	125.5	C17
128.8	126.4	C18	128.7	124.9	C11	128.4	125.2	C9
128.4	125.4	C15	128.4	124.7	C15	127.7	124.7	C11
128.3	124.3	C11 and C17	128.1	124.1	C17		124.6	C15
128.2	124.1	C9	125.6	123.8	C10		124.5	C18
127.9	123.5	C16	-	123.2	C16		123.8	C10
127.4	123.4	C10	-	121.9	C18		123.6	C16
127.3	122.1	C14	-	122.1	C8		121.4	C8
			-	120.9	C12			C12
71.3	70.8	C3	79.1	77.2	C3	78.8	76.0	C3
52.0	54.6	C1	47.7	45.9	C1	45.2	46.1	C1
47.7	50.8	C2	40.5	36.1	C2	39.3	45.0	C2

Figure 3: A table to compare the calculated to literature ¹³C shifts for (3R,5S)-3,5-Diphenyl-3H-dihydro-2-furanone and (3R,4S)-3,4-Diphenyl-3H-dihydro-2-furanone. Dashes in the literature column are used where CH-Ar signals overlapped experimentally. Asterixes denote corrected values using the 0.96δ + 12ppm carbonyl correction.

Structure	13C NMR files
3,4-Diphenyl-3H-dihydro-2-furanone	DOI:10042/to-7400
3R,5S-Diphenyl-3H-dihydro-2-furanone	DOI:10042/to-7401
3S,5R-Diphenyl-3H-dihydro-2-furanone	DOI:10042/to-7390

Figure 4: The NMR files

The ¹³C NMR calculations provide a means of easily distinguishing between regioisomers, with the aliphatic carbon shifts being particularly useful for characterisation purposes. The 3 aliphatic carbons (1, 2 and 3) follow the same ordering in chemical shifts (3, 1, 2) for both regioisomers due to the atoms within the ring core to which they are bound. The deshielding effect of the oxygen to which C3 is bound is stronger than the deshielding effect of the carbonyl functional group to which C1 is bound and C2 is bound to no electronegative atoms/groups and thus is the most shielded. The "natural" chemical shifts of the 3 aliphatic carbons are then perturbed by the aromatic ring currents of the phenyl substituents. Fortunately, perturbation of the chemical shift by phenyl substitution does NOT affect the ordering of aliphatic carbons. This implies that the effect of the phenyl ring substitution is relatively small compared to the electronegativity effect of the oxygen atom and the electron withdrawal of the carbonyl groups. Whilst the perturbation of the "natural" chemical shifts is not large enough to affect ordering of the environments, it is still large enough to be distinguishable in calculations and experiment.

The deshielding a carbon experiences upon substitution with a phenyl ring can be understood in terms of the aromatic ring current. When a carbon is substituted with a phenyl ring, the aromatic ring current will deshield carbon substituents by reinforcing the applied magnetic field, leading to higher chemical shifts. When a carbon is not substituted by a phenyl ring, this extra deshielding is not present. The substitution pattern can therefore be determined by consideration of ¹³C spectra.

There are a number of differences between the experimentally determined spectra and the computed spectra, which reflect the limitations of the model. The main limitation is the inability of the model to reflect equivalence via free rotation about sigma bonds. In reality, the C-Ph bonds would be freely rotating, which would make carbons 14 and 18, 17 and 15, 8 and 12 & 9 and 11 equivalent and they would have an average signal from the two environments due to fluxionality effects on the NMR timescale. The inability to allow for free rotation about sigma bonds results in carbons that should be equivalent being treated as inequivalent and the chemical shift is not averaged across both signals

The carbonyl shifts also showed marked differences between literature and calculated values pre-correction by the provided formula. This is proposed to be the result of a poorly modelled solvent effect of CDCl₃ upon the chemical shift. Chloroform is a polar solvent and so could be expected to have specific interactions with polar functional groups, which may affect the chemical shift of carbons within these polar functional groups.

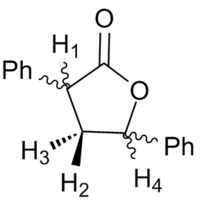
Using ¹H NMR ³J values to assign diastereoisomers in the 3,5 substituted products

Protons coupling	3R, 5S			3R, 5R
	Dihedral Angle between protons /°	Calculated Coupling Constant /Hz	Literature Coupling Constant /Hz	Dihedral Angle between protons /°	Calculated Coupling Constant /Hz	Literature Coupling Constant /Hz
H1 to H2	-105.2	2.0263	8.4	42.6	6.0226	8.5
H1 to H3	15.2	9.6305	12.8	164.0	11.6055	8.5
H4 to H2	100.3	2.1007	5.6	91.5	1.2789	5.4
H4 to H3	-18.9	9.2117	10.8	-30.0	8.1838	7.3

Figure 5: A table to show the calculated coupling constants between selected hydrogens in an attempt to distinguish diastereoisomers

Figure 5: The referencing system used in the ¹H assignments

The calculated ³J values give a relatively poor agreement to literature and cannot be used to assign diastereoisomers computationally. A number of journals have reported failures of the Karplus equation in modelling ³J values in both the original equation and modifications containing empirical corrections. The Karplus equation should therefore only be used in order to determine relative magnitudes. The previously discussed free rotation about C-Ph sigma bonds may have some effect upon the conformation of the 5 membered ring in solution.

It has been reported that ¹H ³J couplings are sensitive to electronegative substituents which affect the coupling. They've been reported to change the overall magnitude of the Karplus equation and cause a shift in the maxima and minima of the curve. The effects of electronegative atoms have been reported to be difficult to model and so the proximity of an ester group to the protons in question probably does not help this computational prediction. It is important to note that ³J couplings of protons are a powerful tool in assigning diastereoisomers, as is evident by comparison of literature values. It was disappointing this procees could not be recreated computationally.

What is the cause of Regio- and Diastereoselectivity in the ring opening of the epoxide?

The reaction gives two regioisomers. For each of these regioisomers there are two possible diastereoisomers. Giving 4 possible products provided different enantiomeric forms of each diastereoisomer are treated as equal. This begs the question: why are only 3 products seen?

Furthermore, why is a regioselectivity of 79: 21 seen? And why is a diastereoselectivity of 56: 44 seen for the 3,5 substituted product and complete diastereoselectivity seen in the 3,4 product?

Whilst it is tempting to jump in and model all of these potential products and calculate their energies, a more considered approach needs to be taken. The ring opening of epoxides is effectively irreversible due to the relief of ring strain. The generated 5 membered lactone is unlikely to break apart and reform an epoxide and an enolate. Thermodynamic control is therefore not accessible in this reaction and the reaction is controlled by kinetics. The transition state of the reaction cannot be modelled using Molecular Mechanics techniques as previously discussed and transition state modelling techniques are currently unfamiliar to me. In order to elucidate the cause of Regio- and Diastereoselectivity in the reaction, a conformational analysis of the proposed transition state will be examined.

The epoxide used in the reaction is racemic i.e. both enantiomers exist in a 50:50 mixture. These enantiomers are shown in Figure 6.

Figure 6: The two enantiomers of Styrene oxide

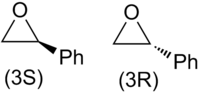
From the mechanistic considerations shown in Figures 2 and 3 it's seen that there are two possible reaction pathways for each epoxide enantiomer that are competing. The possible attacks of the enediolate on(3S)-styrene oxide are shown in Figure 7.

Figure 7: Attacks of enediolate on (3S)-styrene oxide

It is seen that attack on the most hindered position of the epoxide gives steric clashes in the transition state between the two phenyl groups. It is now evident why this product is not observed experimentally. The approach of the nucleophile is disfavoured by steric congestion at the electrophilic centre and experiences steric clashes in the transition state - thus is of a high energy.

The competing ring opening reaction has minimal steric congestion at the electrophilic centre and avoids steric clashes in the transition state. This reaction will therefore be much faster and dominate S-epoxide ring opening.

The opening of the R-epoxide is considered in Figure 8.

Figure 8: Attacks of enediolate on (3R)-styrene oxide

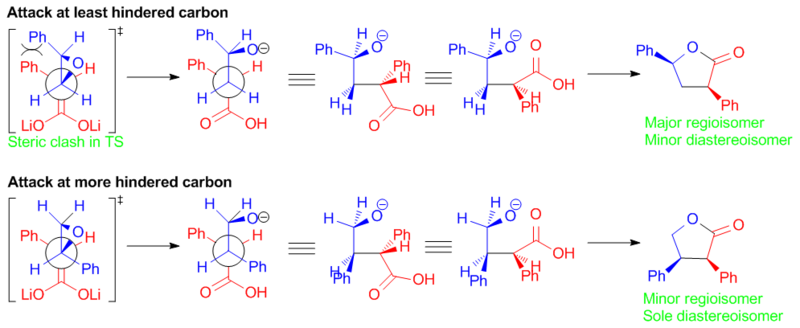
In the ring opening of the R-epoxide, it can be seen that neither reaction dominates as in the case of attack on the 3S epoxide. Attacking the least hindered position avoids steric congestion on the approach, but goes through a high energy transition state. Attack at the most hindered position results in a sterically hindered approach, but goes via a lower energy transition state.

A less one sided competition for the R-epoxide results in the syn-3,5 substituted product being the minor diastereoisomer. The near exclusive formation of the anti-3,5 substituted product leads to no anti-3,4 substituted product being observed experimentally.

Conclusion

Whilst molecular mechanics, semi-empirical molecular orbital theory and DFT-based molecular orbital methods have been demonstrated to be useful in solving some of the chemical problems in this exercise, it was occasionally found that a pen, paper and a bit of chemical knowledge proved far more effective.

In places, the discussed computational methods were highly useful tools. This was the case in the prolinol derivatives exercise, the hyperstable alkene exercise and the dichlorocarbene exercise. Without the explored techniques, the cause of the discussed experimentally observed effects would've been hard to determine.

In the case of the mini-project however, regioisomers and diastereoisomers could've easily been distinguished with a ¹H NMR spectrum, which is quick to acquire experimentally. Enantiomers could've been distinguished experimentally by optical rotation. When these points are taken into consideration, it is hard to justify the computational time spent on this mini-project.

Whilst the accuracy of the computed ¹³C NMR shifts by the GIAO method was impressive in places, the method is severely limited by treating molecules statically. Equivalence of atoms via sigma bond rotation is shown by numerous common chemical moieties and thus the applicability of a static approach is inevitably very restricted. Polar functional groups also appear to be poorly treated, possibly due to a poorly modelled solvent effect of the NMR solvent.