Rep:Mod:bb407

Inorganic Computational Chemistry Lab

Vibrational Analysis

Vibrational analysis calculations are a function of the potential energy surface (PES) with respect to equilibrium geometry's bond length. The particular function used is a second derivative.

Using this calculation, the output provided information regarding the optimised structure. The optimisation can give an indication of whether the ground or transitional states are most stable. The output also allows for the analysis of the structure's vibrational frequencies.

By analysing the vibrational frequencies, information on the structure can be deduced. Positive frequencies throughout the output data indicate an optimised geometry in the ground state. A single negative frequency in amongst the positive, is an indication of a transitional state. Multiple negative frequencies means that the molecular structure needs further optimisation.

In the following exercise, the optimisation must take place prior to vibrational analysis. The model used was the RB3LYP calculation. A basis set has to be used in conjunction with the calculation. The basis set that was chosen was the LANL2MB. This set was used as the calculations involve optimising a molecular structure that contains chlorine.

As a second row atom, chlorine needed the more complex basis set to accomodate its electronic structure.

BCl₃

Diagram	3D Representation
	BCL3

Optimised Structure

B-Cl Distance (Å)	1.87
Bond Angle (Degrees)	120

Optimisation Calculation

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2MB
Energy (a.u.)	-69.44
Dipole Moment (D)	0.00
Point Group	D3H
Time (s)	21.0

Frequency Calculation

File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2MB
Energy (a.u.)	-69.44
Dipole Moment (D)	0.00
Point Group	D3H
Time (s)	17.0

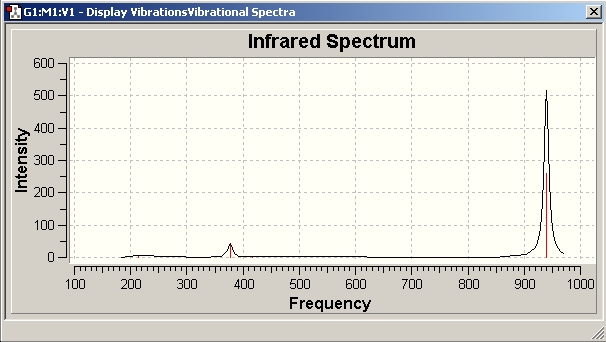
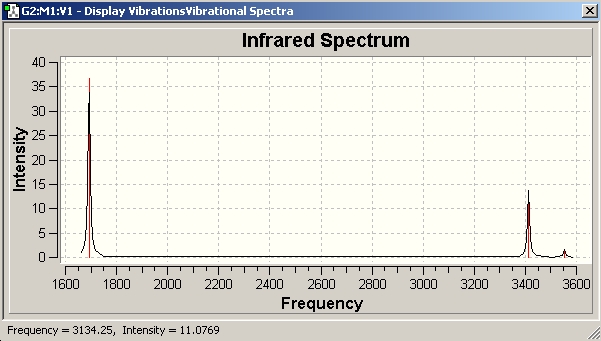
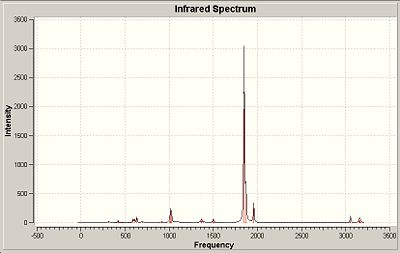
BCl₃ Vibrational Analysis

The data provides an IR spectra from which further anaysis was made.

Vibration Diagram	Intensity	Frequency (cm-1)	Symmetry: D3H	Vibration Desciption
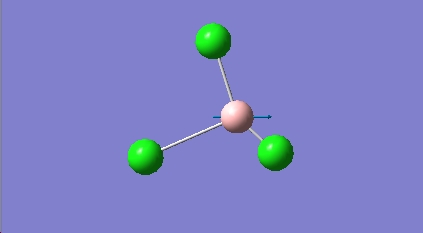
	258.67	939.47	Assymmetric Stretch E'	Boron oscillates along B-Cl bond
	258.67	939.47	Assymmetric Stretch E'	Boron oscillates perpendicular to plane of molecule
	0.00	417.38	Symmetric Stretch A1'	Chlorine atoms oscillate in time along B-Cl bonds
	43.78	376.94	Assymmetric Stretch A2	Boron oscillates perpendicular to plane of molecule; Slight movement of Chlorine atoms
	3.94	214.13	Assymmetric Bend E'	Two B-Cl bonds scissor in plane; Remaining B-Cl oscillates along bond
	3.94	214.13	Assymmetric Bend E'	Single B-Cl oscillates in plane of molecule

On inspection of the data it is apparent that the vibrational frequencies are all positive. This means that the molecule is at a ground state. The mathematical implication is that the molecule has reached a nadir for the bond length with respect to PES.

As expected, the molecule has the correct number of vibrational frequencies. This is based on the vibrational modes afforded to non-linear molecules; 3n-6. Simple spectroscopic theory provides the rationale to interpret the data. Dipole moments provide the activity in infra-red spectroscopy. The symmetric A₁' stretch produces no change in dipole moment, and as a result is inactive.

Degenerate E' sets have a difference as a result of variance between strecthing and bending. The B-Cl bending vibration is located at 214.13 cm^-1; B-Cl stretch vibrations at 939.47 cm^-1. The intensity difference again correlates to stretching having a greater change than the bending vibrations.

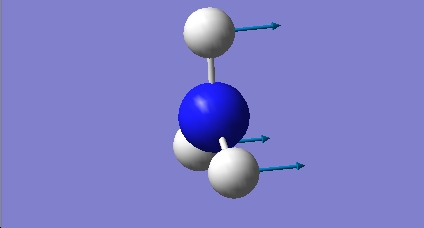
H₂O

For the optimisation of this molecule, which is composed of much simpler component atoms than BCl3, the 3-21G basis set was used in conjunction with the RB3LYP method. A simpler basis set is sufficient to adequately model the electronic structure.

Diagram	3D Representation
	H2O

Optimised Structure

B-Cl Distance (Å)	1.00
Bond Angle (Degrees)	104.0

Optimisation Calculation

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Energy (a.u.)	-75.97
Dipole Moment (D)	2.24
Point Group	C2V
Time (s)	21.0

Frequency Calculation

File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	3-21G
Energy (a.u.)	-75.97
Dipole Moment (D)	2.24
Point Group	C2V
Time (s)	16.0

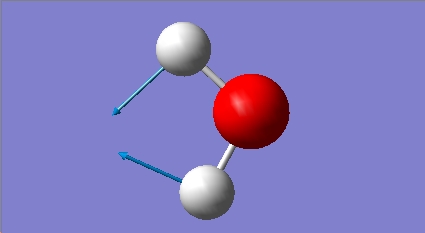
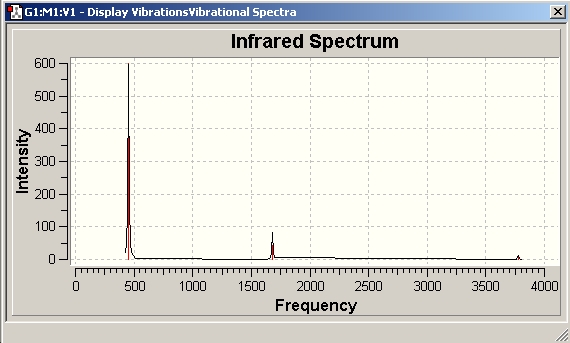
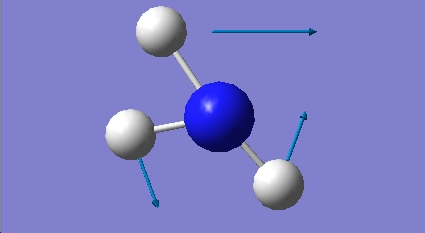
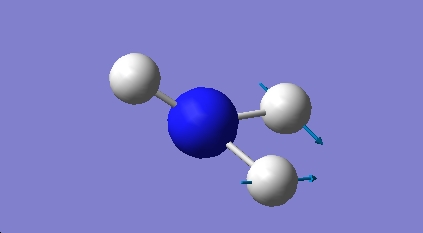
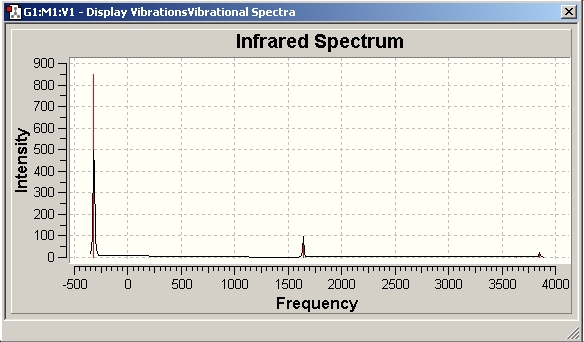
H₂O Vibrational Analysis

The data provides an IR spectra from which further anaysis was made.

Vibration Diagram	Intensity	Frequency (cm-1)	Symmetry: C2V	Vibration Desciption
	1.56	3553.34	Assymmetric Stretch B1	Oxygens oscillate out-of-time to each other along O-H bonds
	13.71	3412.40	Assymmetric Stretch A1	Oxygens oscillate in-time with each other along O-H bonds
	36.74	1692.47	Bend A1'	O-H bonds move in a scissoring action

On inspection of the data it is apparent that the vibrational frequencies are all positive. This means that the molecule is at a ground state. The mathematical implication is that the molecule has reached a nadir for the bond length with respect to PES.

As expected, the molecule has the correct number of vibrational frequencies. This is based on the vibrational modes afforded to non-linear molecules; 3n-6.

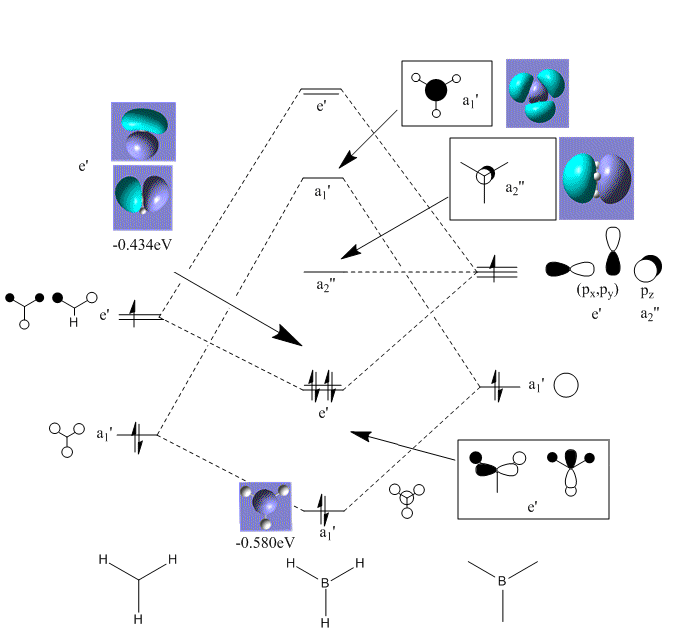
BH₃ Molecular Orbital Analysis

Using Gaussview a Molecular Orbital (MO) diagram was put together. The example used was BH₃, which was covered during previous lecture courses.

The MO diagram produced is very helpful in providing a qualitative arguement for reactivity. In order for BH₃ to complete its octet, it requires two more electrons. It is a well known fact that BH₃ is lewis acidic. The a2" orbital shows that the MO occupies a large and broad area above and below the plane of the molecule, allowing for easy attack from a lewis base.

Interestingly, Gaussview predicted four filled MOs. However, the omitted MO was significantly lower in energy and so left out on the basis that this was an artefact of the prediction process.

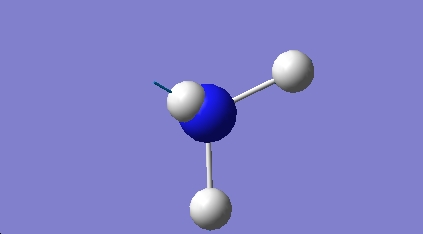
NH₃

In this section, ammonia is to be studied as it possesses the ability to tunnel between PES minima. This means that the structure can invert in a process that superficially is not dissimilar to the inversion on Sn2 centres. This provides two equivalent mirror states with C3V symmetry and a transition state with D3H.

To investigate further the RB3LYP calculation was used again in conjunction with the 6-31G basis set.

NH₃ Optimisation Calculation

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Energy (a.u.)	-56.53
Dipole Moment (D)	1.32
Point Group	C3V
Time (min)	1:14

NH₃ (Long Bond) Optimisation Calculation

In order to perform this optimisation, symmetry was ignored while one of the N-H bonds was given a set distance of 1.01Å.

This produces a variance in symmetry and in the computing time that was required. The energy difference between the long bond optimisation and the normal optimisation is insignificant.

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Energy (a.u.)	-56.53
Dipole Moment (D)	1.34
Point Group	C1
Time (min)	2:20

There was a significant increase in calculation time. This has been attributed to the methods by which Gaussview runs the calculation. Without the symmetry elements the calculations take longer as the program cannot use symmetry to 'shortcut' the process.

NH₃ (High Symmetry) Optimisation Calculation

By using another atom as a 'dummy' the geometry of the molecular structure is forced to maintain a specific chosen shape.

The structure is now in D3H symmetry, explaining the speedy calculation time.

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Energy (a.u.)	-56.53
Dipole Moment (D)	0.00
Point Group	D3H
Time (min)	0:31

NH₃ (RMP2-FU) Optimisation Calculation

In the following optimisation calculations the RMP2-FU method was used in conjunction with the 6-311+G(d,p) basis set. The method and basis set should provide a better calculation.

File Type	.log
Calculation Type	SP
Calculation Method	RMP2-FU
Basis Set	6-311+G(d,p)
Energy (a.u.)	-56.43
Dipole Moment (D)	1.66
Point Group	C3V
Time (min)	0:16

NH₃ (RMP2-FU High Symmetry) Optimisation Calculation

File Type	.log
Calculation Type	FOPT
Calculation Method	RMP2-FU
Basis Set	6-311+G(d,p)
Energy (a.u.)	-56.43
Dipole Moment (D)	0.00
Point Group	D3H
Time (min)	0:47

On inspection of all optimisation results; the RB3LYP method provides the lowest energy with the long bond structure. However, the variance between all the energy figures is insignificant.

The barrier to inversion is calculated by taking the difference in energy between the C3V and D3H forms.

By taking the values from the above optimisations, the barrier to conversion was calculated to be 19.21 kJmol^-1. This is comparable to the literature value of 24.3 kJmol^-1.

NH₃ (C3V Symmetry) Vibrational Analysis

Vibration Diagram	Intensity	Frequency (cm-1)	Symmetry: C3V	Vibration Desciption
	7.09	3775.76	Asymmetric Stretch E	Two Hydrogen atoms oscillate out-of-time with each other; Remaining Hydrogen stationary
	7.09	3775.76	Asymmetric Stretch E	Two hydrogen atoms oscillate together and the other out-of-time along the bonds
	0.07	3575.43	Symmetric Stretch A1'	Hydrogen atoms oscillate in time along N-H bonds
	41.72	1680.47	Bend E	Two N-H bonds scissor in plane; Remaining B-Cl oscillates in plane side-to-side
	41.73	1680.47	Bend E	Two N-H bonds scissor in plane; Remaining B-Cl still
	599.47	452.30	Bend A1	Nitrogen oscillates perpendicular to the plane

The results have all positive frequencies showing a ground state structure.

NH₃ (D3H Symmetry) Vibrational Analysis

Vibration Diagram	Intensity	Frequency (cm-1)	Symmetry: D3H	Vibration Desciption
	19.60	3854.27	Asymmetric Stretch E'	Two Hydrogen atoms oscillate in-time with each other; Remaining Hydrogen out-of-time
	19.60	3854.27	Asymmetric Stretch E<'/P>	Two Hydrogen atoms oscillate out-of-time with each other; Remaining Hydrogen stationary
	0.00	3653.71	Symmetric Stretch A1'	Hydrogen atoms oscillate in time along N-H bonds
	55.98	1640.59	Bend E'	Two N-H bonds scissor in plane; Remaining B-Cl oscillates in plane side-to-side
	55.98	1640.59	Bend E'	Two N-H bonds scissor in plane; Remaining B-Cl still
	849.113	-318.05	-	Nitrogen oscillates perpendicular to the plane

With a single negative frequency value, the structure is a transition state.

Transition Metal Complex

In this investigation, a transition metal complex will be analysed via its vibrational frequency data. The cis and trans isomers of the Mo(CO)₄(PMe₃)₂complex will be examined.

The structure is much more complex than the previous examples, and as such requires extra effort to optimise. Initially a RB3LYP calculation is completed using the LANL2MB basis set. Then further optimisation using the LANL2-DZ basis set.

Trans Isomer

The Trans Isomer

Trans Spectra

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Energy (a.u.)	-773.36
Dipole Moment (D)	0.00
Point Group	C1
Time (h)	3:32:42.0

The optimisation provides the following data:

	Optimised Calculation	Literature Value
Mo-P Bond	2.029Å	2.426Å
Mo-C Bond	2.029Å, 2.029Å	2.037Å, 2.041Å
P-Mo-P Angle (Degrees)	180.0	176.7
R-P-Mo (Degrees)	117.09, 117.06, 115.68	121.02, 120.52, 111.56

Cis Isomer

The Cis Isomer

Cis Spectra

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Energy (a.u.)	-773.36
Dipole Moment (D)	9.07
Point Group	C1
Time (h)	6:15:21.6

The optimisation provides the following data:

	Optimised Calculation	Literature Value
Mo-P Bond	2.648Å, 2.648Å	2.525Å, 2.533Å
Mo-C Bond	1.982Å, 1.982Å, 2.033Å	1.981Å, 1.983Å, 2.034Å
P-Mo-P Angle (Degrees)	92.9	94.8
R-P-Mo (Degrees)	113.90, 118.26, 118.54	112.9, 114.9, 121.1