Rep:Mod:balthasar13
BH3
Optimisation and Frequency Analysis
Method and Basis Set: B3LYP/6-31G(d,p)
Items:
Item Value Threshold Converged? Maximum Force 0.000142 0.000450 YES RMS Force 0.000093 0.000300 YES Maximum Displacement 0.000561 0.001800 YES RMS Displacement 0.000367 0.001200 YES
Frequencies:
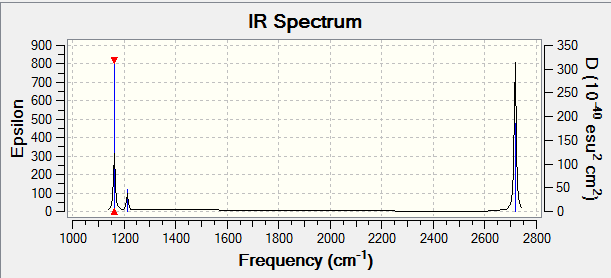
Low frequencies --- -39.8147 -38.4503 -38.4492 -0.0053 0.1238 0.2885 Low frequencies --- 1162.4792 1212.8343 1212.8370
BH3 |
Vibrations
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1162 | 93 | in-plane bend | yes | A2 |
| 1213 | 14 | Scissoring | very little | E' |
| 1213 | 14 | Rocking | very little | E |
| 2584 | 0 | Symmetric Stretching | no | E' |
| 2717 | 126 | Antisymmetric Stretching | yes | A2 |
| 2717 | 126 | Antisymmetric Stretching | yes | E' |
Less than 6 peaks appear in the spectrum as there are several modes of vibration that are degenerate, i.e. they change the shape of the molecule to a tantamount degree. Furthermore, the symmetric stretching motion does not lead to change in dipole and therefore does not register on the IR-spectrum.
MO-diagram
MO-Diagram of BH3
MO-Diagram off Patricia Hunt.[1]
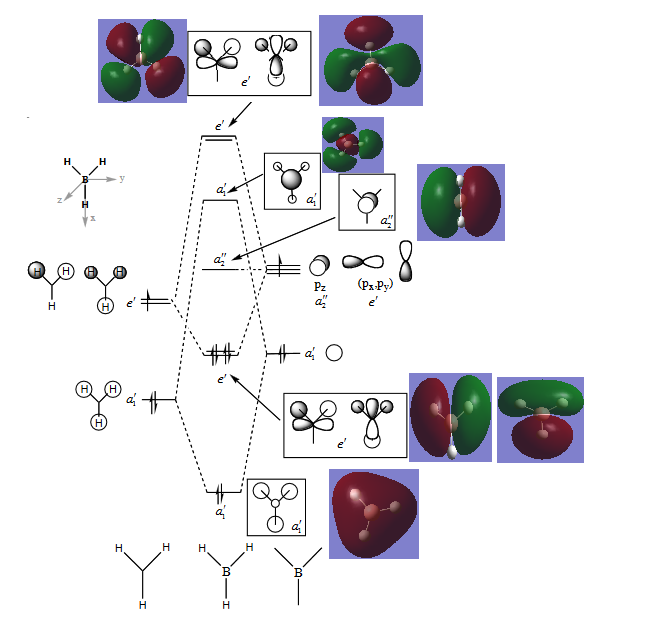
The LCAO ("cartoon") molecular orbitals highly resemble the simulated MOs in shape and phase distribution. However, the simulated MOs are more diffuse and seem to be fused to a certain degree.
This shows that MO theory is a qualitatively good way of determining the MOs of a given molecule since the LCAO of orbitals is enough to show the basic symmetry. The simulated orbitals have a higher degree of accuracy but do not contradict with the LCAOs at any point, only building on top of them.
Smf115 (talk) 07:40, 17 May 2018 (BST)Clear inclusion of the MOs on the diagram and both similarities and differences between the LCAOs and MOs considered.
NH3
Optimisation and Frequency Analysis
B3LYP/6-31G(d,p)
Items:
Item Value Threshold Converged?
Maximum Force 0.000145 0.000450 YES
RMS Force 0.000072 0.000300 YES
Maximum Displacement 0.000568 0.001800 YES
RMS Displacement 0.000284 0.001200 YES
Frequencies:
Low frequencies --- -39.8147 -38.4503 -38.4492 -0.0053 0.1238 0.2885 Low frequencies --- 1162.4792 1212.8343 1212.8370
NH3 |
BH3NH3
Optimisation and Frequency Analysis
B3LYP/6-31G(d,p)
Items:
Item Value Threshold Converged?
Maximum Force 0.000113 0.000450 YES
RMS Force 0.000063 0.000300 YES
Maximum Displacement 0.000615 0.001800 YES
RMS Displacement 0.000354 0.001200 YES
Frequencies:
Low frequencies --- -0.0615 -0.0457 -0.0067 21.6946 21.7004 40.6045 Low frequencies --- 266.0391 632.3710 640.1440
NH3BH3 |
E(NH3)= -26.61532350 E(BH3)= -56.55664155 E(NH3BH3)= -83.22469012
Dissociation Energy:
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] ΔE=-0.05272507 (a.u.) ΔE=-138.429671285 (kJmol-1
Smf115 (talk) 21:52, 15 May 2018 (BST)Well answered first section in general. However, the wrong energy has been used for NH3 (check your linked log file for the correct one) and a comment and comprison of the result was required.
BBr3
GEN/6-31G level
Items:
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000018 0.001200 YES
File:Bb1916 frequency bbr3.log
Frequencies:
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
BBr3 |
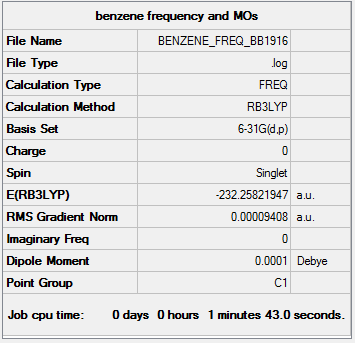
Project on Benzene's and Borazine's Aromaticity
Optimisation and Frequency Analysis
Method and Basis Set: B3LYP/6-31G(d,p)
Items:
Item Value Threshold Converged?
Maximum Force 0.000193 0.000450 YES
RMS Force 0.000094 0.000300 YES
Maximum Displacement 0.000787 0.001800 YES
RMS Displacement 0.000368 0.001200 YES
Frequencies:
Low frequencies --- -11.6728 -0.0007 0.0004 0.0010 6.6686 15.6846 Low frequencies --- 414.0392 414.6031 621.0860
Benzene |
Optimisation and Frequency Analysis of Borazine
Method and Basis Set: B3LYP/6-31G(d,p)
File:File:Borazine summ bb1916.PNG
Items:
Item Value Threshold Converged?
Maximum Force 0.000197 0.000450 YES
RMS Force 0.000067 0.000300 YES
Maximum Displacement 0.000406 0.001800 YES
RMS Displacement 0.000162 0.001200 YES
Frequencies:
Low frequencies --- -17.6663 -11.3513 -9.6682 -0.0007 0.0007 0.0008 Low frequencies --- 288.9706 289.5190 404.2288
Borazine |
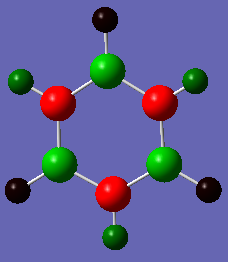
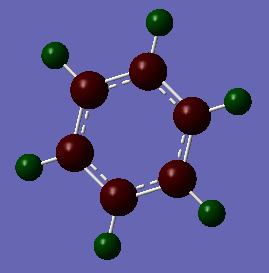
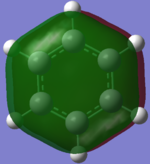
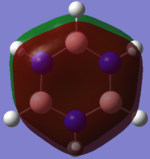
Charge Distribution
Borazine:
The colour scheme goes: the more negative the charge the redder the atom and the greener the atom the more positive it is. Therefore the green atoms in the ring show Boron atoms whereas the red ones represent Nitrogen. Nitrogen is more negative due to its higher electronegativity. The colour differences are very pronounced due to the stark differences of electronegativity between nitrogen, boron and hydrogen.
Atom No Charge H 1 -0.07655 H 2 0.43198 H 3 -0.07654 H 4 0.43198 H 5 -0.07655 H 6 0.43198 B 7 0.74697 B 8 0.74696 B 9 0.74700 N 10 -1.10241 N 11 -1.10242 N 12 -1.10241
Benzene:
The red atoms are the more electronegative Carbon and the green ones represent Hydrogen. The colour differences are less extreme due to the smaller differences in electronegativity between Carbon and Hydrogen.
Atom No Charge C 1 -0.23854 C 2 -0.23854 C 3 -0.23855 C 4 -0.23854 C 5 -0.23854 C 6 -0.23856 H 7 0.23855 H 8 0.23854 H 9 0.23855 H 10 0.23855 H 11 0.23855 H 12 0.23855
It can be seen that the charges are distributed very differently between benzene and borazine. In benzene the negative charge is distributed equally over the Carbon atoms and the positive charge over the Hydrogens. This can be explained by Carbon's higher electronegativity along with the π-System attracting the electrons to the inner ring. In borazine the charges are not as evenly distributed. Hydrogen has a lower electronegativity than Nitrogen but a higher one than Boron. Therefore, the Hydrogen atoms have positive or negative charges depending on which atom they are bonded to. If they are bonded to Nitrogen the difference in electronegativity is signficantly higher and therefore the charge difference is much higher as well.
Smf115 (talk) 07:39, 17 May 2018 (BST)Thorough tabulation of the charges and the correct colour range was used to highlight the chrage distributions across the molecules.
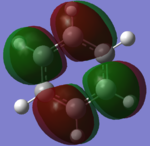
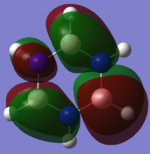
MO Comparison
| level | benzene | borazine | comment |
| 7 |  |
 |
This is the first fully bonding, in-phase molecular orbital of both molecules. The Hydrogens bonded to Boron do not participate in this MO. Rather, the MO of borazine is much less symmetric. |
| 17 |  |
 |
This is the lowest energy combination of the pz orbitals of both benzene and borazine. It can be clearly seen that the combination of the p-orbitals spreads over the whole molecule for both benzene and borazine. However, the coverage of benzene seems to be greater |
| 22 |  |
 |
This is the LUMO of both benzene and borazine. Almost all the p-orbitals are out of phase with their neighbours and combine into an anti-bonding molecular orbital. The MO of benzene is more evenly shaped and symmetrical, though. |
Smf115 (talk) 07:37, 17 May 2018 (BST)Nice comparison however, the charcter of the MOs and identification of sigma- or pi- orbitals should have been made. Further development by mentioning the point group when mentioning symmetry would also be good.
Aromaticity
An MO diagram of benzene's valence orbitals.[2]
Benzene and borazine are isoelectronic. As opposed to benzene, borazine's ring does not consist of 6 atoms of the same element but rather it consists of alternating boron and nitrogen-atoms. This leads to an unequal distribution of the electrons and the electrons involved in the π-bonds are not as delocalised as they are in benzene. However, borazine still obeys the 4n+2 rule and equal bond lengths between Nitrogen and Boron suggest that even while being unequally distributed the electrons are delocalised to a certain extent. In order to benefit from the delocalisation of the π-System Hückel's rules need to be obeyed. They state that the number of electrons needs to equal 4n+2 where n is an integer. Furthermore, all p-orbitals need to be in the same plane and cyclic, to accommodate that the molecule needs to be approximately planar. Although there are exceptions, these rules hold up relatively well. However, it has to be noted that these are approximations and not the proper explanation for the effects that are observed.
To build such a delocalised π-System, molecular orbital theory has to be considered. In MO theory, the Linear Combination of the Atomic Orbitals (LCAO) of the p-orbitals perpendicular to the plane of the ring yields a number of bonding and anti-bonding orbitals. Benzene has 6 p-orbitals which can combine in 6 unique ways; there are 2 combinations which are degenerate with another combination resulting in 4 discreet energy levels - 2 stabilising and 2 destabilising. The 4n+2 rule arises from the fact that the lowest energy orbital is filled by 2 electrons whereas each subsequent orbital requires 4 electrons - bar the highest energy level. Therefore, 6 electrons are needed to fill all the bonding orbitals granting benzene and borazine great stabilisation by mixing its orbitals.
Borazine seems to exhibit some aromatic tendencies but due to the heterogeneous nature of the ring the aromaticity of the ring is interrupted by ionic interactions as well.
Smf115 (talk) 07:35, 17 May 2018 (BST)Good mention of the isoelectronic nature of the two molecules, however, more relevant points could have been made and it needed to be discussed why overlapping pZ AOs is not an accurate descriptor of aromaticity. Reference to the MOs just viewed would have been nice to see but the LCAO idea was different to see.
Smf115 (talk) 07:40, 17 May 2018 (BST)Overall a clear and well srtuctured wiki with a well answered first section.