Jump to content

Rep:Mod:babes

From ChemWiki

Introduction

Molecular mechanics is a way of manipulating the structural configuration of a molecule in order to achieve a minimal structural energy (more than one structure is possible). The methods consider van der Waals forces, torsion strain, bond angle, steric effects and bond length to find the minimum energy. Not all possible factors are considered and this page will use Mechanical methods applied to chemical problems to try and solve/analyse them.

The Hydrogenation of Cyclopentadiene Dimer

Dimer Formation

The dimerisation of cyclopentadiene can produce an exo dimer (1) or an endo dimer (2). The mechanism is a cycloaddition and involves 2 components: a π4s system and a π2s system.

Cyclopentadiene Dimerisation Reaction

After running MM2 calculations on ChemBio3D Ultra 12.0, the following energies were evaluated:

Table 1
Dimer Number 1 2
Stretch 1.28 1.25
Bend 20.57 20.86
Stretch-Bend -0.83 -0.83
Torsion 7.68 9.50
Non-1,4 VDW -1.42 -1.51
1,4 VDW 4.25 4.30
Dipole/Dipole 0.38 0.44
Total Energy/ kcal/mol 31.89 34.02


We can see in Table 1 that dimer 2 is has a higher total energy, which is from a greater torsion energy. Looking at the configuration of the carbon atoms around the new C-C bond for both dimers, there is a clear difference. Dimer 2 is in the gauche configuration, where dimer 1 is in the anti-periplanar. Both configurations are the minimal energy conformations, but in this case, anti-periplanar is slightly more favourable by ~1.9 kcal/mol. Hence, the endo dimer is the kinetic product and the exo dimer is the thermodynamic. The endo dimer is specifically produced in this cyclo dimerisation, so the reaction is kinetically controlled.






Hydrogentation

Hydrogenation of dimer 2 produces product 3 and 4. Initially, only one of these is produced (kinetic product) and later the other is produced (thermodyanmic product).

Table 2
Dimer Number 3 4
Stretch 1.28 1.36
Bend 19.09 13.03
Stretch-Bend -0.84 -0.56
Torsion 11.14 12.43
Non-1,4 VDW -1.65 -1.34
1,4 VDW 5.79 4.43
Dipole/Dipole 0.16 0.14
Total Energy/ kcal/mol 34.97 29.25


A comparison of the information from the simulation on ChemBio 3D Ultra suggests that product 3 is produced first and product 4 is produced over time. The total energy of product 3 is greater than product 4, this is facile. The difference in energy of the two products is mainly due to a higher bend energy in product 3. The difference between the products is which double bond is hydrogenated. Most of the strain in bond angle is in the bridging methyl and the removal of a double bond would ease this strain. The bond hydrogenised in product 4 gives a lower energy, but why? This bond is closer to the bridging methyl so would have a greater effect on easing this strain than the one in product 3.





Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

The following reactions was analysed using MM2, MMFF94 and the MOPAC molecular orbital method. This is because there is a bug in the programme which affects calculation of molecules with N+ atoms in its structure. Only the MM2 and MMFF94 methods are affected, so the results from the MOPAC method are the ones which should be analysed. The first two methods are just to configure the structure roughly so the final calculation is quicker.

Reaction of molecule 5 and 6

The MeMgI reagent (Grignard’s Reagent) was not included in the calculation because when attempted, an error occurred stating that ‘No atom type was assigned to selected atom’. This is from the programme not being able to process the magnesium atom.

The carbonyl and 7 member ring were moved about to try and find alternate conformations which gave an energy minima. Table 3 shows these results.

Table 3
Conformation Number 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9
Dihedral Angle/ degrees 28.82 25.75 28.53 28.85 28.83 28.38 28.49 17.95 25.78
Heat of Formation/ kcal/mol 93.70 93.91 93.69 93.69 93.69 93.68 93.69 101.80 93.92



Molecule 5.6: Lowest Energy Conformation of Molecule 5
Molecule 5


Graph 1: Graph showing Dihedral angle against Heat of formation

Table 3 and graph 1 show that as the dihedral angle increases, the stability of compound 5 increases. The carbonyl is pointing above the 6 member ring relative to the amide oxygen.

The stereo selectivity originates from the carbonyl group, specifically the oxygen. The Mg from the reagent co-ordinates to the oxygen, as oxygen is electronegative and magnesium is electropositive. When the Mg co-ordinates to the carbonyl, the methyl group will attack from the same side as the carbonyl is pointing (above the ring). The mechanism of the reactions displays the selectivity of the reagent. The halogen of the Grignard reagent co-ordinates to the amide oxygen [1], stabilising molecule 5.a whilst Mg co-ordinates to the carbonyl group. [1]


The reaction with MeMgI is highly regio- and stereo-selective (19:1), but bulkier alky groups show greater selectivity (>99:1). [1]

Reaction of molecule 7 and 8

The reaction of 7 to 8 will be higher stereo- and regio- selective as the alkyl group is considerably more bulky than the in the previous reaction. Finding energy minima was alot more facile due to aromatic rings holding most of the structure in place. Only part of the 7 member ring and the substituents on the nitrogen next to the oxygen could be moved to try and find energy minima.

Table 4
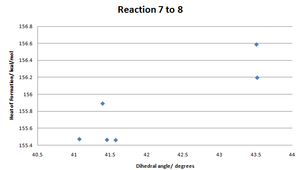
Conformation Number 7.1 7.2 7.3 7.4 7.5 7.6
Dihedral Angle/ degrees 43.52 43.51 41.39 41.45 41.57 41.07
Heat of Formation/ kcal/mol 156.20 156.59 155.89 155.47 155.46 155.47


Molecule 7.5: Lowest Energy Conformation of Molecule 7
Molecule 5

The general pattern seems to be that as the dihedral angle increases, so does the minimal energy for that conformation.

Graph 2: Graph showing Dihedral angle against Heat of formation

The reagent in this case is not Grignard but NH2Ph which is sterically bulky so this dominates the stereo selectivity of the molecules attack. S. Leleu et al [2] states that amines react on the opposite face with respect to the carbonyl lactam. This arises from steric control by the carbonyl lactam. Therefore, the amine must attack para to the N+ atom.

Improvements

This model could be improved by calculating the optimum transition state with and without the Grignard reactant in the calculation. ChemBio3D Ultra doesn’t allow calculations with metal atoms, Gaussview does and doing a Density Function Theory Method may allow this sort of calculation.

A possible further investigation would be to hinder the movement of the carbonyl sterically. Possibly by having bulky substituents (e.g methyl groups instead of hydrogens on the 7 and 5 member rings) or making the 5 member ring aromatic to reduce the flexibility of the 7 member ring.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Molecule 9 and 10

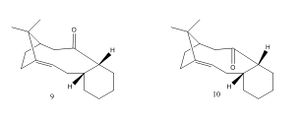
During the synthesis of taxol, an important intermediate is formed which has forms 2 atropisomers. Antropisomerism originates from high energy barriers when rotationg around a single bond. [3] Molecule 9 and 10 are the two isomers and reveals that the orientation of the carbonyl group dictates the total energy of the molecule.

Table 5
Conformation Number 9.1 9.2 9.3 9.4 9.5
Position of Carbonyl (with respect to 6 member ring) Up Up Up Up Up
MM2 Energy/ kcal/mol 55.82 50.45 55.93 61.15 55.90
MMFF94 Energy/ kcal/mol 80.16 74.33 80.18 86.92 80.19
Table 6
Conformation Number 10.1 10.2 10.3 10.4 10.5 10.6 10.7
Position of Carbonyl (with respect to 6 member ring) Down Down Down Down Orthogonal Orthogonal Orthogonal
MM2 Energy/ kcal/mol 54.69 43.16 52.33 48.19 123.44 166.86 134.92
MMFF94 Energy/ kcal/mol 76.49 61.22 74.43 66.79 This calculation moved the carbonyl upwards, suggesting this is not a minimum for this calculation. 249.21 This calculation moved the carbonyl upwards, suggesting this is not a minimum for this calculation.


Molecule 10.2 Molecule 10.5 Molecule 9.2
Molecule 10.2
Molecule 10.5
Molecule 9.2

The different energys for each orientation of the carbonyl group comes from different conformations of the 6 member ring. The lowest conformation for the carbonyl orientation upwards is a chair conformation and for downwards is also a chair conformation. The downwards orientation provided the most stable conformation, overall. The MMFF94 method produced the same results but gave them a higher energy. Notably, MMFF94 did not find all the orthogonal orientations, so you could arrugue that MM2 is better in the respect that is has more energy minimas.

Alkene Hyper stability

If an alkene is hyperstable is will be inert to hydrogenation [4], it is stated that molecule 9 and 10 react abnormally slow across the carbon-carbon double bond suggesting this is a hyperstable alkene. Hyperstable alkenes arise if there is less strain in the system when the double bond is present, than if it were not. This is common with bridge head positions, like the one in molecule 9 and 10.

Modelling Using Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

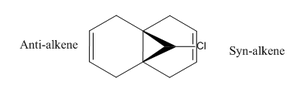
The reactivity of dichlorocarbene is controlled by its orbitals. To analyse this further, the MOPAC method is used to generate an image of the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2. The method used was PM6.

Molecule 12






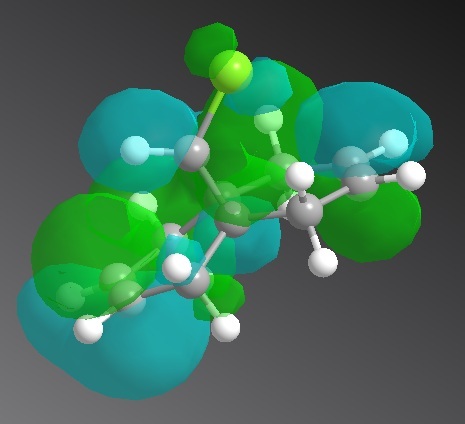
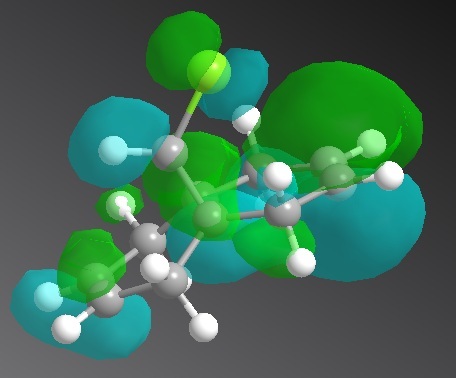
Positive: Lime Negative: Aqua

HOMO -1 HOMO LUMO LUMO +1 LUMO +2


The HOMO shows high electron density on the syn-alkene, suggesting it has a higher nucleophilicity than the anti-alkene. Skell et al [5] say that dichlorocarbene reacts as an electrophile, therefore, it will prefer to attack the syn-alkene over the anti-alkene. Studying the HOMO-1 and LUMO +1, there is a potential interaction on the anti-alkene bond between the π-orbital of this bond and the Cl-C σ*in the LUMO +1 as their conformation is anti periplanar to each other. The effect of this is to stabilise the HOMO-1 by 0.08eV, according to Rzepa et al [6]. Not only this, but the HOMO-1 becomes more delocalised, therefore electron density will be less on the anti-alkene, hence less nucleophilic character. Experimentally, these factors were displayed by Halton et al [7] (shown below).

Vibrational Frequencies

The vibrational frequencies were calculated using Gaussview. The molecules analysed were molecule 12 and the hydrogenated anti-alkene in 12 (12h).

The aim is to inspect the effect of C-Cl on vibration frequency and the effect of the removal of a carbon-carbon double bond.

Table 7:Computational and literature values
Bond Computational Value (Molecule 12)/ cm-1 Computational Value (Molecule 12h)/ cm-1 Literature Value/ cm-1 [8]
Syn-alkene C=C bond 1757.36 1758.06 1620-1680
Anti-alkene C=C bond 1737.11 N/A 1620-1680
C-Cl 770.91 774.96 600-800


The C-Cl bond frequency matches the literature value and there is no significant change after hydrogenation. However, the change suggests the C-Cl bond is more rigid after hydrogenation of the anti-alkene bond since the frequency is larger, implying that there may have been a minor donation into the C-Cl σ* orbital due to weak interaction from the π bond of the anti-alkene bond. Overall, the C=C frequencies have a higher frequency than the literature value, suggesting that the bonds are more rigid. This originates from π bond and C-Cl σ* orbital interactions, which is strong from the syn-alkene but not the anti-alkene. The double bonds are in a ring system which reduces there flexibility, also. The computational values imply that the syn-alkene is more rigid than the anti-alkene, therefore contradicting the previous conclusion that the syn-alkene was more reactive.

Further Substituents

Table 8:Computational and literature values
Bond Computational Value (Molecule 12.BH2)/ cm-1 Computational Value (Molecule 12.CN)/ cm-1 Literature Value/ cm-1 [8]
Syn-alkene C=C bond 1756.55 1756.53 1620-1680
Anti-alkene C=C bond 1657.19 1706.25 1620-1680
C-Cl 759.05 765.77 600-800

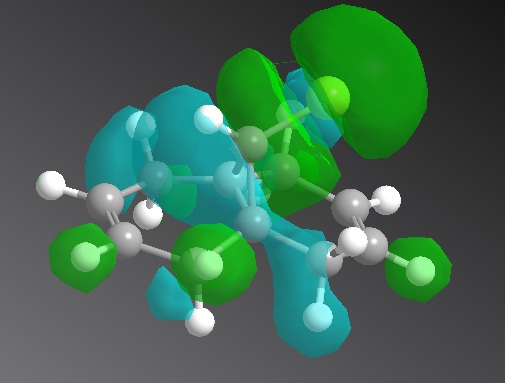
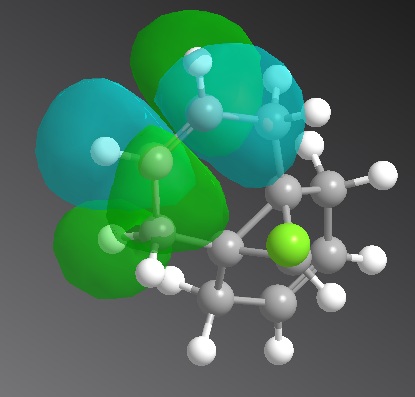
The C-Cl bond frequency still matches the literature and the C=C is larger than the literature, as reasoned above. The syn-alkene peak does not change with substituents added to the anti-alkene but the anti-alkene decreases in frequency. This is implies that the anti-alkene bond is weakened by the substituents.

Structure based Mini project using DFT-based Molecular orbital methods

The reaction shown below was investigated by Balci et al [9] and is believed to have only 2 stereospecific products and 1 nul reaction at particular conditions. We are interested in distingushing between the 2 stereospecific isomers.

Mini Project Reaction

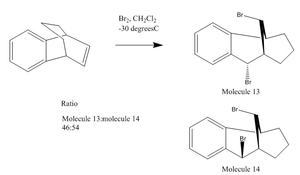
The stereoselectivity of this reaction will be looked at computationally and derive, from calculations, which isomer is most stable. The method used was DTF with a base function of 6-31g. The difference in energy between the two molecules is 6.47 kcal/mol with molecule 13 being the higher energy. This is not consitent with Balci's results as he had moleceule 13 more stable than 14 by 1.685 kcal/mol. The difference in results can be attributed to the use of different calculation methods, I used mpw1pw91/6-31g(d,p) with 25 cycles to optimise, where Balci used (B3LYP/6-31G(d)).

13C NMR

Balci's Data Molecule 13 13C NMR (100 MHz, CDCl3) δ 137.5, 136.7, 130.2, 128.5, 128.5, 127.3, 57.5, 54.8, 44.5, 42.4, 35.4, 32.9, 15.8 Molecule 14 13C NMR (100 MHz, CDCl3) δ 137.5, 136.7, 130.2, 128.5, 128.5, 127.3, 57.5, 54.8, 44.7, 42.5, 35.4, 32.9, 15.7

Molecule 13 Molecule 14
Molecule 10.2
Molecule 10.2
Table 9: Calculated Data: Molecule 13
δ/ppm Element Atom Number
23.74 H 17
24.20 H 16,15
24.48 H 18
25.43 H 19
27.21 H 26
28.63 H 25
29.17 H 20
29.24 H 21
29.65 H 23
29.83 H 22,24
58.85 C 5
66.09 C 4
68.97 C 3
71.45 C 1
72.60 C 6
72.84 C 2
126.98 C 7
130.68 C 12
146.55 C 11
148.55 C 8
162.18 C 10
171.07 C 9
2348.94 Br 14
2595.12 Br 13
Table 10: Calculated Data: Molecule 14
δ/ppm Element Atom Number
23.76 H 17
24.13 H 16
24.19 H 15
24.42 H 18
26.38 H 19
27.42 H 26
28.55 H 25
28.94 H 20
29.63 H 22
29.69 H 23
30.09 H 24
30.23 H 21
59.21 C 5
66.34 C 4
67.76 C 3
71.34 C 1
72.33 C 6
72.97 C 2
133.95 C 7
137.95 C 12
146.95 C 11
148.58 C 8
164.04 C 10
166.86 C 9
2149.11 Br 14
2457.91 Br 13

Values have been edited with respect to Rzepa et al [10]


Looking at the peaks that correspond to the Br atoms, there is a difference of about 40ppm in one of the shifts. This is because Br is electronegative and they are closer in molecule 14, hence they interact through space, deshielding the atoms and moving the peak to wards the deshielded end of the spectra. If we consider the Karplus equation [11] we can predict that there would be a difference in the coupling constant when looking at carbon 7 and 8 since the dihedral angle between the hydrogens on these carbons is different. Molecule 13 would have a low coupling constatnt, where molecule 14 would be higher. The literature values do correspond with the calculated values with minor deviation. This is due to the error in the calculation of approximatly 2ppm, larger is poosible as it is not a fixed value.

IR

There is a difference in intensity of one of the peaks of the IR at 1250cm-1. This maybe due to overlap of peaks in the IR and not due any real distinguishable difference in the molecules vibrations.

IR: Molecule 13
IR: Molecule 14

Mechanism Discussion

The literature provides a mechanism with transition state energies.

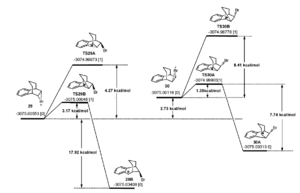
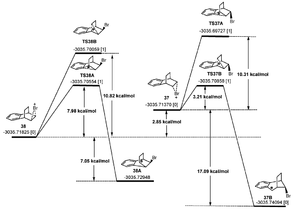
Taken from the literature: Transition state energy diagram
Taken from the literature: Transition state energy diagram 2

Initially, the bromine can attack from either face of the C=C bond. The direction of attack has no impact on which molecule (13 or 14) is favoured, however the diagrams on the right do explain why only these 2 isomers are produced. Looking at the final molecules of each transition, either molecule 13 and 14 are produced (from molecule 29B and 37B) or an alternative is produced from molecule 30A and 38A. Molecule 30A and 38A are higher in energy than 29B and 37B, however, the transition state to produce 30A and 38A is higher in energy than 29B and 37B. Hence, we can say that molecule 13 and 14 are the kinetic and thermodyanmic product when compared to the product of 30A and 38A. However, the energy of the products of 30A and 38A is not known so this may not be the case.


References

  1. ↑ 1.0 1.1 1.2 A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
  2. ↑ S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
  3. ↑ Bringmann G, Mortimer AJP, Keller PA, Gresser MJ, Garner J, Breuning M (2005). "Atroposelective Synthesis of Axially Chiral Biaryl Compounds". Angewandte Chemie International Edition 44 (34): 5384–5427. doi:10.1002/anie.200462661. PMID 16116589.
  4. ↑ Maier, W.F.; Schleyer, P. v. R. J. Am. Chem. Soc. 1981, 103, 1891
  5. ↑ Philip S. Skell, M. S. Cholod J. Am. Chem. Soc., 1969, 91 (25), pp 7131–7137 DOI: 10.1021/ja01053a040 http://pubs.acs.org/doi/abs/10.1021/ja01053a040
  6. ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
  7. ↑ B. Halton, S.G.G. Russell, J. Org. Chem., 1991, 56, 5553: DOI:10.1021/jo00019a015
  8. ↑ 8.0 8.1 http://www2.ups.edu/faculty/hanson/Spectroscopy/IR/IRfrequencies.html
  9. ↑ Metin Balci, et al, J. Org. Chem., 2007, 72 (13), pp 4756–4762 DOI: 10.1021/jo070253b
  10. ↑ C. Braddock and H. S. Rzepa, J. Nat. Prod., 2008, 71, 728-730. DOI:10.1021/np0705918
  11. ↑ Dalton, Louisa (2003-12-22). "Karplus Equation". Chemical & Engineering News 81 (51): 37. http://pubs.acs.org/cen/science/8151/8151karplus.html.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:babes&oldid=818674"