Rep:Mod:azaleacomp

Transition States and Reactivity Computational Lab

.log files can be found here.

Transition structures are notoriously difficult to predict due to their fleeting lifetime; they cannot be captured or observed directly meaning that experimentally energy differences can be calculated, but true energy values cannot. As a result, certain mechanistic details of chemical reactions remain ambiguous and, at times, cannot be justified. Transition states can, however, be predicted theoretically through programs such as Gaussian, which run calculations based on quantum mechanics and the Schrödinger equation. As a result of the numerous approximations and assumptions that these theories rely on, computational experiments often lead to deviations from reality.

Gaussian is able to calculate energies by consideration of the different attractive/repulsive forces in a chemical reaction and comparing this to a system in which the same atoms are infinitely far apart (at a relative energy of zero). Through this, it's able to create potential energy surfaces (PES) in which positions on the curve correspond to different types of conformations and states; minima represent stable conformations such as reactants, products and intermediates whilst maxima represent transition states. Note that in either case, the gradient of the turning points will be equal to zero. This is a key principle that the programme relies on in order to locate the position of transition structures^[10].

Through Gaussview, this experiment explored the reaction paths for the well-known Cope rearrangement and Diels Alder cycloaddition reactions, by characterisation of their transition states and calculation of activation energies.

The Cope Rearrangement

By following instructions from the Transition States and Reactivity ChemWiki^[1], this tutorial provided an introduction to various computational techniques.

Figure 1: Concerted Mechanism of the Cope Rearrangement

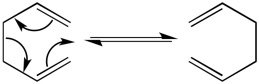
The Cope rearrangement is a pericyclic [3,3]-sigmatropic rearrangement of 1,5-hexadiene, thought to pass from one form to another through either a 'chair' or 'boat' transition state via a concerted mechanism^[1], into one of its structural isomers. Although the 'boat' TS lies slightly higher in energy than its 'chair' conformer, it is still ambiguous which transition state dominates. By calculating this rearrangement we are hence able to locate low-energy minima and transition structures to confirm and quantify this.

Optimising the Reactants and Products

Since 1,5-hexadiene contains sp³-hybridised C-C bonds, there are numerous conformations in which it can exist^[2]. Two of these, antiperiplanar and synperiplanar (gauche), were constructed and optimised in Gaussview. These structures could then be compared to known energies^[1] to determine which conformer had been optimised.

Figure 2: Anti- and Syn- Newman Projections

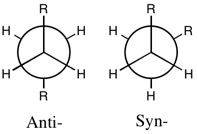
1,5-Hexadiene Anti-1 Conformation

After constructing and 'cleaning' an antiperiplanar (180^o dihedral angle) conformation of 1,5-hexadiene, the structure was optimised at the Hartree-Fock/3-21G level of theory to obtain the minimum energy. Note that although the 'clean' function optimises the structure of a molecule to a certain extent, it does not provide an accurate enough value to use in further calculations. A 'symmetrise' function was then applied to determine the point group of the resulting structure.

The optimised structure matched most closely with the anti-1 conformation.

Structure	Energy	Point Group
	-231.69260235 a.u.	C2

1,5-Hexadiene Gauche-1 Conformation

In a similar way, a synperiplanar or gauche (62.75° dihedral angle) conformation of 1,5-hexadiene was optimised at the Hartree-Fock/3-21G level of theory to obtain the minimum energy, followed by a 'symmetrise' function.

The optimised structure matched most closely with the gauche-1 conformation.

Structure	Energy	Point Group
	-231.68771617 a.u.	C2

The steric clash due to the proximity of the alkene groups on this conformer can account for the higher energy compared to anti-1.

1,5-Hexadiene Gauche-3 Conformation

After constructing, optimising (HF/3-21G) and symmetrising the gauche-3 conformation, it can be seen that the energy of this conformer is lower than in anti-1. This observation is strange as, explained above, you would expect the unfavourable gauche interactions to increase the energy with respect to the antiperiplanar conformer. One explanation for this could be accounted for by additional stabilising interactions seen between the two π-orbitals in the MO computation^[3].

Structure	Energy	Point Group	Computed MOs
	-231.69266120 a.u.	C1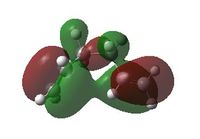

Nf710 (talk) 23:23, 19 January 2016 (UTC) Well done for looking at the orbitals to prove the relative energies

1,5-Hexadiene Anti-2 Conformation

Finally, the anti-2 conformation was constructed, optimised at the Hartree-Fock/3-21G level of theory, and 'symmetrised'. In order to obtain a value for the point group, the 'symmetrise' function had to be performed with relaxed tolerance. In addition, the conformation was also optimised at the Density Functional Theory/B3LYP/6-21G* level of theory (a higher level of theory to that used previously)

Structure	Energy (HF/3-21G)	Energy (DFT/B3LYP/6-21G*)	Point Group
	-231.69253528 a.u.	-234.61171063 a.u.	Ci

To confirm that the DFT optimisation was properly minimised, and hence suitable to compare to experimentally measured quantities, an additional frequency calculation was carried out to look at the vibrational frequencies. After confirming that all vibrational frequencies were real and positive, the two levels of theory were compared by looking at the overall geometry change (energies were not compared since it is meaningless to compare the energies of different levels of theory). Note that the following table is showing the bond lengths and distances of half of the hexadiene molecule as they are identical on either side.

The two methods of calculating energies that have been adopted so far, Hartree-Fock and Density Functional Theory, both use the Born-Oppenheimer approximation. The HF method solves the many-electron Schrödinger equation with a single Slater determinant, neglecting electron interactions and becoming expensive at larger basis sets. On the other hand the DFT level of theory is more precise as it takes into account pairing energy and spin, as well as minimising electron density to avoid overestimation, generally making it a more expensive calculation to run^[4]. The basis set used in a calculation determines how well the electrons can be 'moulded' around the molecule. The larger the basis set, the closer the calculated value to the true energy. In this instance two small basis sets are being used, meaning the HF method is the less expensive one. The 3-21G and 6-21G basis sets are similar in that they describe valence AO with two functions and other core AO with just one (known as split-valence basis sets).

Nf710 (talk) 23:27, 19 January 2016 (UTC)6-32G(d) uses d orbitals for polarisation using a too high basis for a simple calcuation can work against you. But very good knowledge of the methods.

(i) Geometry Comparison

Basis Set	Bond Type	Length	Bond Type	Angle
HF/3-21G	C1=C2 (terminal)	1.31613 Å	C1=C2-C3-C4 (dihedral angle)	-114.669°
	C2-C3, C3-C4	1.50891 Å, 1.55275 Å	C1=C2-C3	124.806°
DFT/B3LYP/6-21G*	C1=C2 (terminal)	1.33350 Å	C1=C2-C3-C4 (dihedral angle)	-118.600°
	C2-C3, C3-C4	1.50419 Å, 1.54816 Å	C1=C2-C3	125.300°

From analysis of bond lengths, bond angles and the point group of each level of theory, it is obvious that the two basis sets show only very small differences in geometry. Hence it can be reasoned that both these molecules are at the same point on the PES and that for the types of system being analysed in this report, a lower level of theory can be adopted for geometry calculations as they will give a similar result than that calculated at a higher level of theory.

Nf710 (talk) 23:32, 19 January 2016 (UTC) Well concluded. nice comparison

(ii) Frequency Calculations

Mentioned previously, in the optimisation of the anti-2 conformation, a frequency calculation was run (at 298K) simultaneously to ensure all vibrations were real. A negative, or imaginary, value for a vibrational frequency tells us that we have instead acquired a transition state rather than a critical point. In the IR spectrum acquired below, it can be confirmed that the optimised anti-2 conformer was indeed a critical point.

Nf710 (talk) 23:33, 19 January 2016 (UTC) Critical point is a weird way to describe it. use minimum in future.

Figure 3: IR Spectrum of Anti2 Conformation of 1,5-Hexadiene

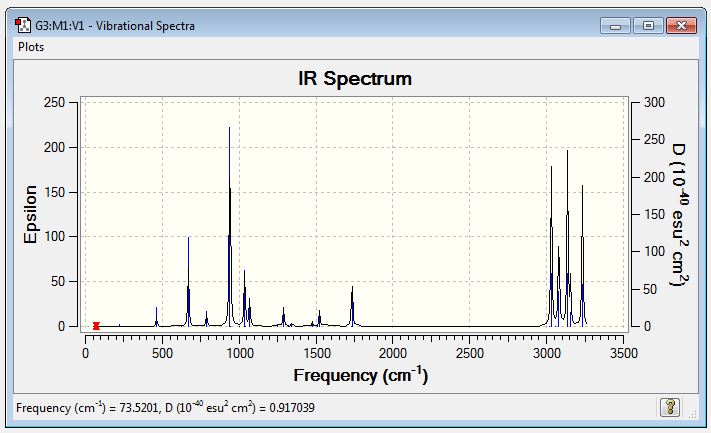
By running this frequency calculation we were also able to access a number of other quantities. In order to make some comparisons, the same frequency calculation was additionally carried out at 0K.

Sum of electronic and zero-point energies = 298 K: -234.469219 a.u., 0 K: -234.469219 a.u.

The sum of electronic and zero-point energies is identical for both temperatures, which makes sense as this value represents the potential energy at 0 K and hence the minimum energy a quantum mechanical system can contain. In this instance, the zero-point energy constitutes residual vibrational energy due to the fact that all the bonds in the molecule are modelled by a harmonic oscillator.

Sum of electronic and thermal energies = 298 K: -234.461869 a.u., 0 K: -234.469219 a.u.

Here, we can see that at a higher temperature, the energy is higher due to additional contributions from translational, vibrational and rotational energy modes^[5].

Sum of electronic and thermal enthalpies = 298 K: -234.460925 a.u., 0 K: -234.469219 a.u.

The equation for the enthalpy, H = E + RT, can be used at constant pressure and takes into account the temperature of the system. Therefore at a higher temperature there will be a larger contribution to thermal enthalpies, whilst at T = O K there will be no additional contributions.

Sum of electronic and thermal free energies = 298 K: -234.500809, 0 K: -234.469219

The equation for the Gibbs' free energy, G = H - TS can be used at constant pressure and takes into account the entropy of the system.

Nf710 (talk) 23:35, 19 January 2016 (UTC) Well done for doing it at different temperatures! although you should have done something other than 0K as obviously they were all going to be the same.

Optimising the 'Chair' and 'Boat' Transition Structures

There are two possible transition state conformations of the Cope rearrangement that enable a concerted rearrangement. In this section, these were analysed by optimising their transition structures and studying their Intrinsic Reaction Coordinate pathway to compare activation energies. IRC calculations also helped determine which of the conformers of 1,5-hexadiene the calculated transition state led to.

Since transition state optimisations are more difficult than minimisations, a few different calculation methods were used and compared. The chair transition structure was optimised via two different methods, first by computing force constants and then by the frozen coordinate method and the boat transition state was optimised via the QTS2 method.

Chair TS Optimisation: Computing Force Constants

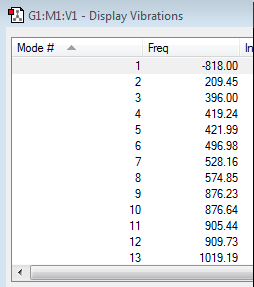
After having created a guess structure for the chair transition state consisting of two HF/3-12 optimised allyl fragments placed 2.2 Å apart, the 'guess' molecule was optimised to a TS(Berny). As before, a frequency calculation was also carried out, however this time an imaginary frequency of -818.00 cm^-1 was necessary to confirm a transition state had been calculated.

The reason why this negative frequency corresponds to a transition state can be understood if we consider at the 1D quantum harmonic oscillator. At any transition state, the force constant, k, is negative since the force and displacement of the molecule are in opposite directions; this value can be obtained by calculating the second derivative of the PES, which will be negative due to a downwards curve in all directions. As a result, when the frequency is calculated using w = sqrt(k/m) we are left with an imaginary number.

Nf710 (talk) 23:37, 19 January 2016 (UTC) well explained but you could have formatted the equation better

It is important in this type of calculation that the 'guess' TS resembles the actual TS as closely as possible since the calculation follows the negative direction of curvature, or the reaction coordinate. Here, this is done by computing the force constant matrix in the first step of the optimisation, which is then continually updated as the calculation is run.

Once completed, an animation of the negative vibration was run to confirm it corresponded to the Cope rearrangement.

Vibrations		Energy
Figure 4: Vibrations of the TS(Berny) Optimised Chair Structure by Computing Force Constants		-231.61932228 a.u.

Chair TS Optimisation: Frozen Coordinate Method

This method of TS optimisation comes in useful if the guess transition state structure is too far from the exact structure for method (i) to be effective. In this way, certain bonds are frozen in place while the remaining unfrozen atoms of the molecule are minimised before a final transition state optimisation can be run. It can also be beneficial as, on occasion, force constants need not be calculated like they are for method (i).

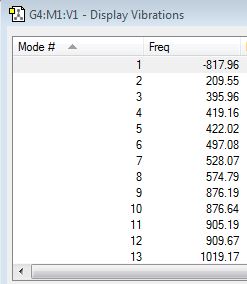
Here, the distance between the terminal carbons on each allyl fragment were set to 2.2 Å then frozen, the rest of the molecule was minimised using a HF/3-21G basis set and finally HF/3-21G/TS(Berny) optimisation was run. An imaginary frequency of -817.96 cm^-1 was acquired suggesting that again a transition structure has been reached.

Since the same level of theory and basis set was used for both types of chair optimisation, it can be useful to compare the energies obtained. Here, the energy difference between the two is very small (in the order of 10^-7) which would suggest that the original 'guess' structure was close enough to the actual chair TS geometry.

Vibrations		Energy
Figure 5: Vibrations of the TS(Berny) Optimised Chair Structure using Frozen Coordinate Method		-231.61932245 a.u.

Boat TS Optimisation: QTS2 Method

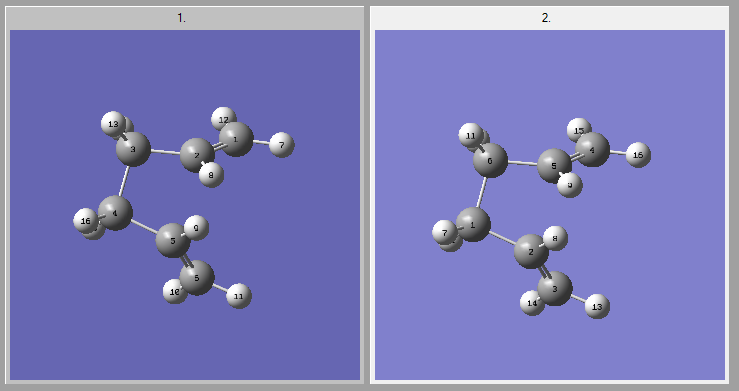
This alternative transition state geometry was optimised using the QST2 method. This is a chain of state method which uses the geometries of the starting material and final product to interpolate a structure for the transition state. In order for this transition state optimisation to be successful, care must be taken on numbering the atoms on the reactant and product 1,5-hexadiene molecules to show where each atom moves to during the rearrangement.

After an initial attempt at optimising the structure, the bond angles on both molecules had to be adjusted to represent the desired transition state more closely (the C2-C3-C4-C5 dihedral angle was set at 0^o and C2-C3-C4 at either end was set at 100^o). Changing the structure of the reactant and product in this way enabled a more successful TS calculation to be run.

Once optimised, the vibrations were checked for an imaginary frequency (-840.22 cm^-1).

Figure 6: Numbered Reactant and Product 1,5-Hexadiene Molecules

Vibrations
Figure 7: Vibrations of the TS(QTS2) Optimised Boat Structure

Next a QTS3 calculation was attempted, in which a third 'guess' TS structure is required along with the reactant and product molecules. However, initial attempts did not result in the correct optimised transition state at all; given that the QTS2 method worked much more quickly and easily it was decided that no further attempts would be made.

Nf710 (talk) 23:38, 19 January 2016 (UTC) All your frequencies are correct

Intrinsic Reaction Coordinate Method

The IRC method makes it possible to predict which transition state the rearrangement will pass through, along with the resulting conformer of 1,5-hexadiene. This is done by following the minimum energy path from the TS down the steepest energy slope on the potential energy surface until it reaches a local minimum. You can set this calculation to run in either direction (i.e. towards the reactants or the products) for a set number of steps, making it possible to compare geometries and determine whether the TS is early or late.

Potential issues that can arise when running an IRC include either not setting enough steps (in which case the calculation does not reach a local minimum) or even setting too many (the IRC can sometimes end up following an alternative pathway). Furthermore, the IRC calculation may get confused between an intermediate and a product due to the fact that both have a gradient of zero on the IRC pathway.

Chair TS IRC

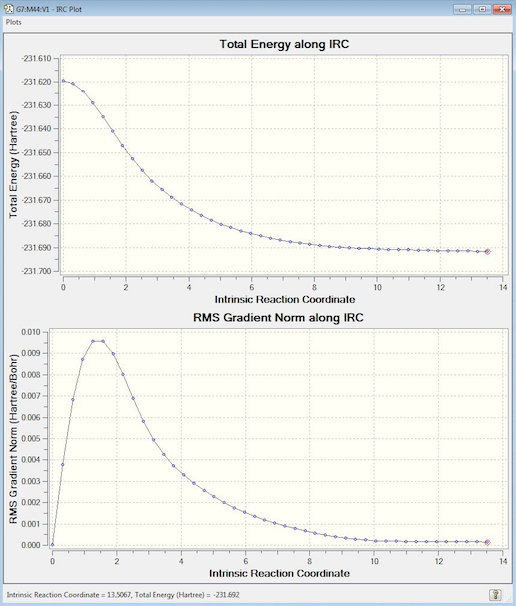
First, an IRC calculation was run on the optimised chair TS found by computing force constants. 50 steps were set, however the calculation converged after 44 to give a plot reaching a minimum with a near-zero gradient at an energy of -231.69157809 a.u.. Comparing this value to appendix 1 in the tutorial, this energy was most closely matched to that of the gauche 2 conformer of 1,5-hexadiene.

In order to confirm this, the 44th structure from the IRC was optimised to a minimum using a HF/3-21G level of theory. The resulting molecule had the expected point group of C2 and an energy of -231.69166702 a.u.

Figure 8: The IRC Plot of the Chair TS

Nf710 (talk) 23:40, 19 January 2016 (UTC) Correct conformer

Calculating Activation Energies

The activation energy of for the Cope rearrangement via both transition structures was calculated by re-optimisation of the chair and boat TS from the HF/3-21G basis set to DFT/B3LYP/6-31G*.

The geometries of the newly optimised TS compared to the TS optimised at a lower basis set appear to be quite similar, seen in the table below.

	Chair TS					Boat TS
Basis Set	Bond Type	Length	Bond Type	Angle	Point Group	Bond Type	Length	Bond Type	Angle	Point Group
HF/3-21G	C-C (Between Fragments)	2.02026 Å	C-C-C (Allyl)	120.502 °	C2h	C-C (Between Fragments)	2.13989 Å	C-C-C (Allyl)	121.670 °	C2v
	C-C (Allyl)	1.38926 Å				C-C (Allyl)	1.38150 Å
DFT/B3LYP/6-21G*	C-C (Between Fragments)	1.96647 Å	C-C-C (Allyl)	119.908 °	C2h	C-C (Between Fragments)	2.20595 Å	C-C-C (Allyl)	122.246 °	C2v
	C-C (Allyl)	1.40764 Å				C-C (Allyl)	1.39329 Å

However when calculating the activation energy in going from 1,5-hexadiene reactant to either transition state at each level of theory and basis set, the results obtained were more noticeably different. The results are shown in the tables below. Note that the electronic energy is calculated by subtracting the zero-point correlation from the sum of electronic and zero-point energies (0 K), and that the activation energy is calculated by finding the difference in relative energies of the anti2 conformation and the TS, then applying 1 a.u. (or Hartree) = 627.509 kcal mol^-1.

	Chair TS			Boat TS			Anti2 Conformer
Basis Set	Electronic + Zero-Point Energies (0 K)	Electronic + Thermal Energies (298 K)	Electronic Energy	Electronic + Zero-Point Energies (0 K)	Electronic + Thermal Energies (298 K)	Electronic Energy	Electronic + Zero-Point Energies (0 K)	Electronic + Thermal Energies (298 K)	Electronic Energy
HF/3-21G	-231.466698 a.u.	-231.461339 a.u.	-231.619322 a.u.	-231.450930 a.u.	-231.445302 a.u.	-231.602802 a.u.	-231.539539 a.u.	-231.532565 a.u.	-231.692535 a.u.
DFT/B3LYP/6-21G*	-234.414912 a.u.	-234.408985 a.u.	-234.556932 a.u.	-234.402347 a.u.	-234.396004 a.u.	-234.543078 a.u.	-234.469219 a.u.	-234.461869 a.u.	-234.611711 a.u.

Chair TS	Activation Energy (HF/3-21G)	0 K : 45.9 kcal mol-1	35% error from literature at 0K
		298 K : 44.7 kcal mol-1	31% error from literature at 0K
	Activation Energy (DFT/B3LYP/6-21G*)	0 K : 34.4 kcal mol-1	1.2% error from literature at 0K
		298 K : 33.2 kcal mol-1	within the literature range at 0K
Boat TS	Activation Energy (HF/3-21G)	0 K : 56.3 kcal mol-1	21% error from literature at 0K
		298 K : 54.8 kcal mol-1	17% error from literature at 0K
	Activation Energy (DFT/B3LYP/6-21G*)	0 K : 43.1 kcal mol-1	within the literature range at 0K
		298 K : 41.3 kcal mol-1	3.3% error from literature at 0K

Literature experimental values at 0 K of 33.5 ± 0.5 kcal mol^-1 (chair TS) and 44.7 ± 2.0 kcal mol^-1 (boat TS)^[1] were found, along with values at 298K of 140 ± 2 kJ mol^-1 (chair TS) and 187.1 ± 8 kJ mol^-1 (boat TS)^[6]. However after converting kJ mol^-1 into kcal mol^-1, the literature values at each temperature were almost identical. So all activation energies calculated were compared to literature at 0K.

From the table above it is clear that the DFT level of theory is much closer in both cases. This means a higher level of theory provides a more accurate estimate for the activation energy. On the other hand there is no benefit of using a higher basis set to calculate geometries, hence often it is more computationally efficient to map the PES in a low basis set the optimise to a higher basis set to determine final quantities. It can also be concluded from these calculations that the chair TS is, indeed, lower in energy than the boat in both levels of theory and basis sets.

Nf710 (talk) 23:44, 19 January 2016 (UTC) In general a very easy to read and well set out report, good use of jmols and a high level understanding of the theory. well done.

The Diels-Alder Cycloaddition Reaction

Figure 10: Concerted Mechanism of the Diels-Alder Cycloaddition

The Diels-Alder reaction is another type of pericyclic reaction, namely a [4+2]-cycloaddition. It constitutes a diene (4π system) and dienophile (2π system) and, like the Cope rearrangement, it is thought to undergo a concerted mechanism via a cyclic transition state, breaking two π-bonds and forming two new C-C σ-bonds. The formation of a cyclic ring provides a strong thermodynamic driving force.

Usually the D.A. cycloaddition is a reversible reaction in which the substituents on the two reactants dictate the position of equilibrium; these substituents also determine the type of [4+2]-cycloaddition (either a normal or inverse electron demand) in which the HOMO-LUMO interactions decide whether or not an interaction is allowed or forbidden. For a reaction to be allowed, the HOMO on one reactant must be able to interact with the LUMO on the other with significant overlap density. Hence, orbitals with different symmetry do not have sufficient overlap to react^[7].

In order to have a favourable reaction, the HOMO-LUMO energy gap must be minimised. Under a normal electron demand this is achieved by having an EDG on the diene which increases the energy of the HOMO and an EWG on the dienophile which lowers the energy of the LUMO, whilst under inverse electron demand an EDG on the dienophile and EWG on the diene is preferred instead. Additional stabilising interactions arising from a substituted dienophile, known as secondary orbital effects, can also affect the position of equilibrium as well as the regiochemistry of the product. This can be explained by the fact that π-orbitals on the substituents are able to interact the new double bond being formed. There are two main types of regioisomers that can be formed; the exo- product and the endo- product.

Now, two different Diels-Alder reactions will be studied by looking at the transition states and the molecular orbitals to have a better understanding of the symmetry and selectivity of the reaction. An AM1 semi-empirical molecular orbital calculation method was used for all Diels-Alder calculations in this section; due to parametrisation of integrals, this method is much faster than methods used previously^[8].

D.A. Cycloaddition of Cis-Butadiene and Ethene

A molecule of cis-butadiene was constructed and optimised with the AM1 semi-empirical method. It was then symmetrised to give a C2V point group and the HOMO and LUMO were plotted. It can be seen that the HOMO is antisymmetric and the LUMO symmetric with respect to the plane through the centre of the molecule (i.e. vertical). An ethene molecule was also optimised in order to take a look at its HOMO and LUMO and the corresponding energies.

Molecular Orbitals	HOMO	LUMO
Figure 11: The Calculated MO of Cis-Butadiene

Molecular Orbitals	HOMO	LUMO
Figure 12: The Calculated MO of Ethene

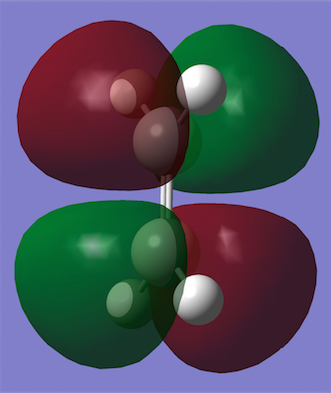Subsequently the transition state geometry was calculated by constructing a guess envelope structure and setting the inter fragment distance to 2.2 Å and the point group to Cs. In this position, the molecule has a maximum overlap of the necessary orbitals. Next the envelope structure was optimised to a TS(Berny) by computing force constants, an additional frequency calculation was run to check for an imaginary frequency and observe the vibration that this corresponds to.

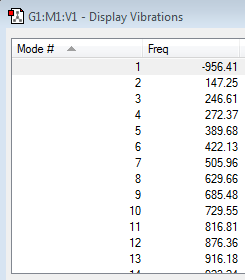
Vibrations	-956.41 cm-1	147.25 cm-1	Energy
Figure 13: Vibrations of the TS(Berny) Optimised Envelope Structure by Computing Force Constants			0.11165465 a.u.

The observed vibration appears to be a concerted D.A. cycloaddition, showing a synchronous formation of the two new bonds. Conversely, the lowest positive frequency exhibits an asynchronous rock.

The HOMO and LUMO were plotted in the same way as for cis-butadiene and by comparing the HOMO-LUMO energy values in cis-butadiene, ethene and this transition state, it was deduced that the reaction is normal electron demand (the energy of the butadiene HOMO is higher than the ethene HOMO). Furthermore, the diene HOMO and the dienophile LUMO (both antisymmetric) combine to give the antisymmetric HOMO on the TS. This is allowed by the Woodward-Hoffman rules since orbital symmetry has been preserved, and it is favourable since their linear combination lowers the energy by the most.

Molecular Orbitals	HOMO	LUMO
Figure 14: The Calculated MO of the Transition State

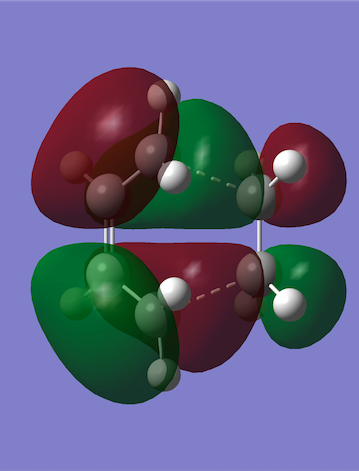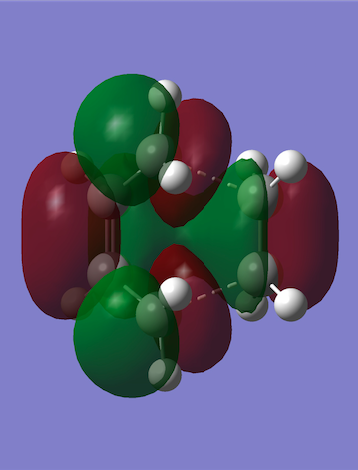An IRC was then run to check that there are no other possible TS or intermediates in this reaction, this time it was run in both directions as the reaction is no longer symmetrical. The IRC calculation converged after 87 steps, with the left hand side corresponding to the cyclic product at -0.0109917 a.u. and the right hand side the reactants at 0.0746277 a.u.; unfortunately the IRC calculated the reverse reaction instead of the desired D.A. cycloaddition. However this isn't a problem as the pathways and energies are still applicable. Since the IRC pathways shows just one peak, it can be assumed that there is just this one transition state, in this case an early TS due to the position of the peak closer to the reactants than the product. Furthermore, the animation demonstrates that the pathway follows the expected concerted mechanism.

Figure 15: The IRC Plot of the Diels Alder Cycloaddition of Cis-Butadiene and Ethene

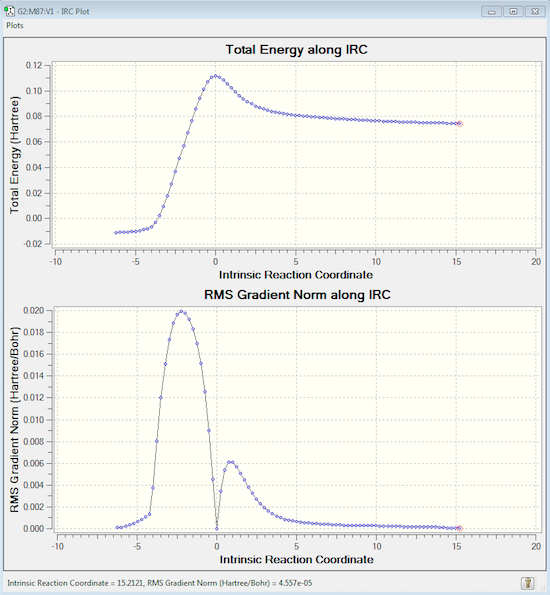
The point group of the transition state was found to be C1 and the interfragment distance to be 2.11922 Å. This value is larger than sp³ C-C (1.54 Å) and sp² C=C (1.34 Å) bond lengths, but less than double the value of the C- atom van der Waals' radius of 3.4 Å^[9]. So although there is definitely not an ordinary C-C bond between these atoms, there must be some form of interaction pulling them together.

D.A. Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

After having analysed the D.A. reaction for a simple system, this can be extended to look at the effect of substituents on the reaction; maleic anhydride is a dienophile containing carbonyl group substituents making it electron poor whilst cyclohexa-1,3-diene is an electron rich molecule due to the -R groups donating electron density into the reactive π-bonds. The second reactant is also asymmetric, leading to two possible trajectories from which the dienophile can approach.

In this section the regioselectivity of the Diels-Alder reaction was studied by considering the effect of secondary orbital effects, this was primarily done by comparison of transition state MO and activation energies.

The Exo- Transition State

A guess transition state was constructed by modifying the guess envelope structure of cis-butadiene and ethene D.A. TS to include the additional substituents mentioned above, whilst paying attention that the correct exo- regiochemistry was constructed. The inter-fragment distance was set to 2.2 Å and the point group set to Cs. Next the guess structure was optimised to a TS(Berny) by computing force constants and an additional frequency calculation was run to check for an imaginary frequency.

Vibrations		Energy
Figure 16: Vibrations of the TS(Berny) Optimised Envelope Structure by Computing Force Constants		-0.05041916 a.u.

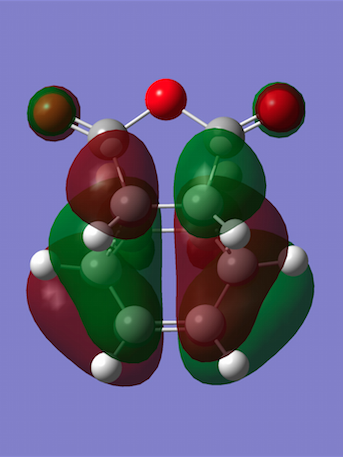
The HOMO and LUMO were plotted and both turned out to be antisymmetric. No secondary orbital interactions are observed since the C=O π* and C=C π orbitals are too far away to interact; a lack of such highly-stabilising interactions results in quite a high-energy transition state. Also note that whilst the HOMO only has nodal planes passing through atoms, the LUMO contains an additional plane between the two approaching reagents (an increased number of nodal planes leads to a higher energy).

Molecular Orbitals	HOMO	LUMO
Figure 17: The Calculated MO of the Transition State

The following IRC was run, which converged after 39 steps. This time the pathway has been calculated in the right direction meaning the left-hand side shows the reactants at -0.0830669 a.u. and the right shows the product at -0.159165 a.u. Since the IRC pathway shows just one peak it can be assumed that there is just this one transition state, plus the animation demonstrates that the pathway follows the expected concerted mechanism.

(From the gradient it looks like it hasn't converged. I suspect the calculation terminated with an error, but it is clear that you have the correct TS Tam10 (talk) 14:48, 11 January 2016 (UTC))

Figure 18: The IRC Plot of the Exo- Product

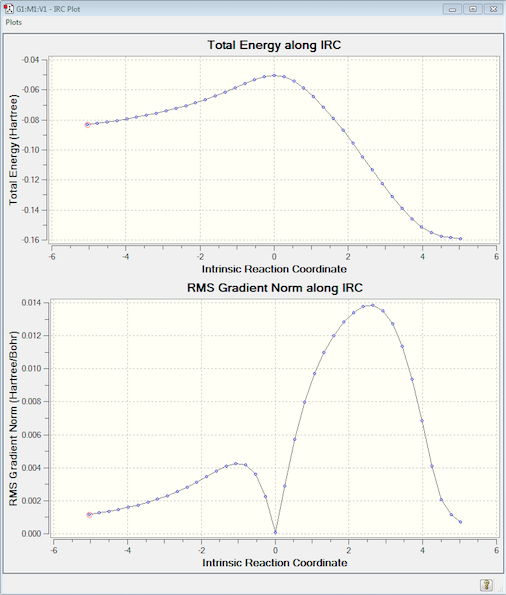
The geometry of the exo- transition state is summarised below. As observed in the previous example, the inter-fragment distance is between that of a single bond and two C- van der Waals' radii, suggesting an interaction but not a bond. Furthermore, the rest of the C-C bonds involved in the reaction reflect something in-between a C-C and C=C bond, mirroring the fact that electrons are moving/delocalised. The C1-C2 bond length is not involved in the D.A cycloaddition and hence remains close to a normal C-C bond length (1.54 Å).

Figure 19: Exo- Transition State

Bond Type	C1-C2	C3-C4	C4-C5	C3-C10	C7-C10
Bond Length	1.52203 Å	1.39437 Å	1.39683 Å	2.17036 Å	1.40996 Å

The Endo- Transition State

The same calculations were performed on a guess endo- transition structure, acquired in the same way as for exo- (but with the maleic anhydride flipped over). It is immediately clear that this transition state is lower in energy than exo-.

Vibrations		Energy
Figure 20: Vibrations of the TS(Berny) Optimised Envelope Structure by Computing Force Constants		-0.05150476 a.u.

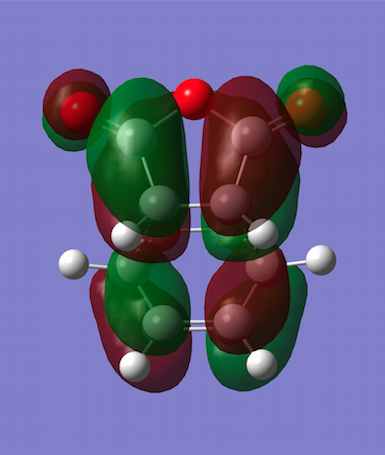
The HOMO and LUMO were plotted, and both turned out to be antisymmetric again. Now secondary orbital interactions can be observed between the dienophile C=O π* and diene C=C π orbitals, which results in greater stabilisation that previously. In this example, the stabilisation is so strong that it overrides steric clashes between the carbon chain from cyclohexa-1,3-diene and the C-O chain close by. Also note that whilst the HOMO only has nodal planes passing through atoms, the LUMO contains an additional plane between the two approaching reagents.

Molecular Orbitals	HOMO	LUMO
Figure 21: The Calculated MO of the Transition State

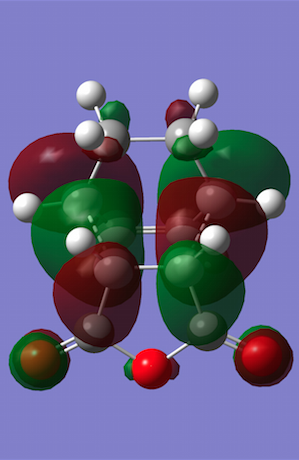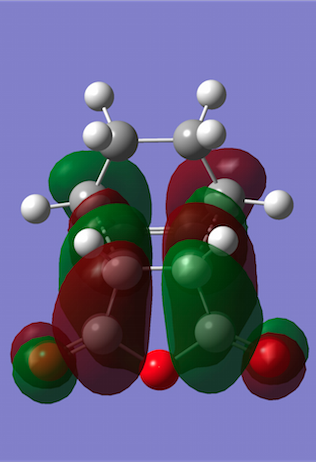The following IRC was run, which converged after 47 steps. This time the pathway has been calculated in the right direction meaning the left-hand side shows the reactants at -0.083664 a.u. and the right shows the product at -0.160026 a.u. Since the IRC pathway shows just one peak it can be assumed that there is just this one transition state, plus the animation demonstrates that the pathway follows the expected concerted mechanism.

Figure 22: The IRC Plot of the Endo- Product

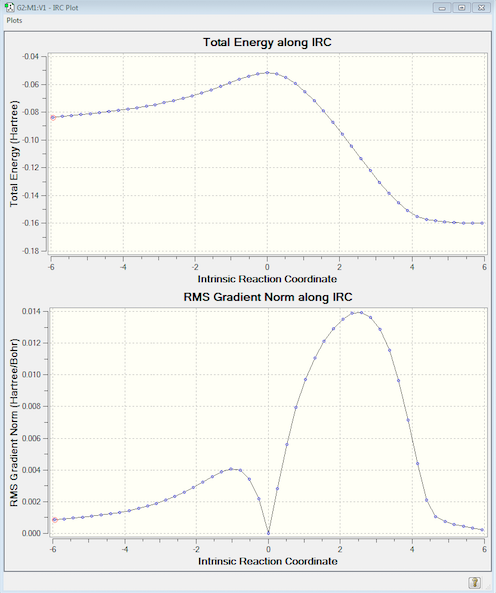
The geometry of the endo- transition state is summarised below. The inter-fragment distance is in between C-C bond and two C- van der Waals' radii, suggesting an interaction but no bond. The rest of the C-C bonds involved in the reaction are approximately equal and in-between the length of a C-C bond and C=C bond due to movement of electrons. The C4-C5 bond which is not involved in the D.A cycloaddition, however, remains close to a normal C-C bond length (1.54 Å).

Figure 23: Endo- Transition State

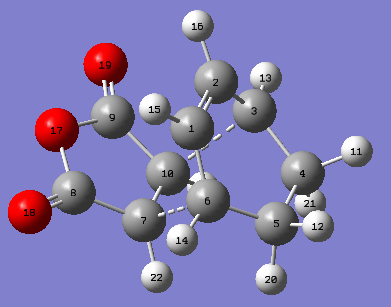
Bond Type	C1-C2	C2-C3	C4-C5	C3-C10	C7-C10
Bond Length	1.39722 Å	1.39303 Å	1.52299 Å	2.16245 Å	1.40849 Å

Calculating Activation Energies

The activation energies for this reaction via both the exo- and endo- transition states were calculated in the same way as before, in order to determine which regioisomer is energetically favoured.

	Maleic Anhydride	Cyclohexa-1,3-diene	Sum of reagents	Exo- TS		Endo- TS
Energy	-0.12182423 a.u.	0.02771124 a.u.	-0.09411299 a.u.	-0.05041916 a.u.		-0.05150476 a.u.
Activation Energy				0.04369383 a.u.	27.4 kcal mol-1	0.04260823 a.u.	26.7 kcal mol-1

The endo- activation energy is lower than for exo-, suggesting this is the kinetic product of the reaction. Also, when looking at the IRC calculations previously the energy of the endo product (-0.160026 a.u.) is lower than that of the exo- product (-0.159165 a.u.), suggesting that it must also be the thermodynamic product.

This energy difference can be explained when comparing the inter-spacial distance of the carbonyl oxygens from maleic anhydride to neighbouring atoms from cyclohexa-1,3-diene in both transition states. Overall, the distances in the exo- transition state are smaller, suggesting the system is more strained than in the endo- product. Another contribution to the larger exo- energy is due to a lack of secondary orbital interactions, mentioned previously.

Conclusion

The first section of this computation experiment studied a pericyclic Cope rearrangement. By looking at the possible transition states that the rearrangement can go through and calculating the activation energies at two levels of theory, HF/3-21G and DFT/6-31G, it was concluded that the chair TS was preferred over a boat TS as it was lower in energy (in both cases). By running the same calculations with two different basis sets, it was possible to compare the effect that they had on the calculated geometries and energies, and the amount by which these differ compared to literature. It became clear that although both methods were quite accurate when it came to calculating geometries, the DFT-6-31G method was much more accurate in calculating energies.

Next, the Diels-Alder cycloaddition was considered. By running similar calculations on two different D.A. reactions (cis-butadiene/ethene and cyclohexa-1,3-diene/maleic anhydride), this time using an AM1 semi-empirical method, it was concluded that the the endo- TS was preferred over the exo- TS due to secondary orbital effects and steric clashes in the exo- isomer. By analysis of the bond lengths across fragments in the transition states it was seen that in every instance, the TS showed a form of interaction that was in-between a bond and van der Waals' interactions.

That said, in both of these cases there will have been a number of factors that computational calculations are unable to take into account and also a number of approximations that are necessary for the calculations to be run. Given that the programme is looking at a single system, simple intermolecular interactions between other molecules are neglected in these calculations, as is the Frontier Orbital approximation, in which a decrease in the HOMO-LUMO energy gap means reactants need not be as close together to react.

References

1. Imperial College London, Computational ChemWiki, Mod:Phys3, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3

2. Loudon, M.; Kantorowski, E. J., Introduction to Alkenes: Structure and Reactivity, Organic Chemistry, 5th Edition, 111 (4), California Polytechnic State University

3. Rocque, B.; Gonzales, J.; Schaffer, H., An Analysis of the Conformers of 1,5-Hexadiene, Molecular Physics, 100 (4), 2002

4. Amusia, M.; Msezane, A.; Shaginyan, V., Density Functional Theory vs. the Hartree Fock Method: Comparative Assessment, Phys Scr, 68 (6), 2003

5. Ochterski, J. W., Thermochemistry in Gaussian, 2000, http://www.gaussian.com/g_whitepap/thermo.htm

6. Suckling, C.; Suckling, K.; Suckling, C., Chemistry Through Models, Cambridge University Press, 1978

7. Knowles, R., The Conservation of Orbital Symmetry, Princeton, MacMillan Group, 2007

8. Hammes-Schiffer, S.; Anderson, H., Ab Inito and Semi-Empirical Methods for Molecular Dynamics Simulations Based on General Hartree-Fock Theory, The Journal of Chemical Physics, 99 (1), 1993

9. Bondi, A., Van der Waals' Volumes and Radii, The Journal of Physical Chemistry, 68 (3), 1964

10. Jensen, F., Introduction to Computational Chemistry, England: John Wiley and Sons Ltd., 1999