Rep:Mod:aza
Module 3
In this experiment, transition structures of larger molecules will be studied. Using molecular orbital-based methods to solve Schrodinger equations numerically and locate transition structures based on the local shape of a potential energy surface so that the geometries of the transition states, the pathway and the barrier heights would be calculated as well.
The Cope Rearrangement Tutorial
Here we are going to study a chemical reactivity problem using [3,3] sigmatropic rearrangement of a 1,5 hexadiene as an example. This reaction involves 6π electrons and follows the 4n+2 rule for aromaticity.
In order to find the most energetically favoured conformer, all possible conformations of the reagent must be optimised first to determine which conformer is the most energetically favourable. Locate the low-energy minima and transition structures on the diene potential energy surface, to determine the preferred reaction mechanism.
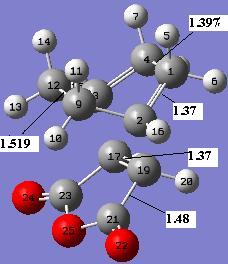
A molecule of 1,5-hexadiene with an "anti" linkage for the central four C atoms is drawn using GaussView. The structure is cleaned and optimised at a HF/3-21G level of theory.
Pentahelicene |
Another molecule of 1,5-hexadiene with a "gauche" linkage for the central four C atoms is created and optimised at the same level of method HF/3-21G.
Pentahelicene |
As there are 3 rotating C-C bonds, and each C-C bond has 3 rotational minima, so the molecule should have 27 conformations. However, there are only 10 of them are energetically distinct due to symmetry and enantiometric relationship.
| Conformer | Structure | Point Group | Energy /a.u. HF/3-21G |
Relative Energy (kcal/mol) |
| gauche1 |
|
C2 | -231.68772 | 3.1 |
| gauche2 |
|
C2 | -231.69167 | 0.62 |
| gauche3 |
|
C1 | -231.69266 | 0.00 |
| gauche4 |
|
C2 | -231.69153 | 0.71 |
| gauche5 |
|
C1 | -231.68962 | 1.91 |
| gauche 6 |
|
C1 | -231.68916 | 2.20 |
| anti-1 |
|
C2 | -231.69260 | 0.04 |
| anti-2 |
|
Ci | -231.69254 | 0.075 |
| anti-3 |
|
C2h | -231.68907 | 2.25 |
| anti-4 |
|
C1 | -231.69097 | 1.06 |
Gauche 3 with a C1 point group has energy at -231.69266122 a.u. which is the lowest energy conformations of 1,5-hexadiene. It will be used as a reference for the calculated activation energies and enthalpies. But the HF method is a really basic calculation method, no electron correlation is considered in the calculation. Now we are going to use a higher level calculation method B3LYP/6-31G* to optimise the anti 2 conformer with a Ci point group. A frequency calculation based on B3LYP/6-31G* optimised structure has also been carried out. The frequency calculation is used to confirm that it is a minimum in this case as there is no imaginary frequency.From the result file, a list of energies with additional terms can be obtained:
| Structure | Energy/a.u. HF/3-21G |
Energy/a.u. DFT/6-31G |
Sum of electronic and zero point charge energies at 0K | Sum of electronic and thermal energies at 298.15K and 1atm | Sum of electronic and thermal enthalpies (correction for RT) | Sum of electronic and thermal free energies (entropic contribution to free energy) | Changes in Geometry by changing the calculation method |
|
-231.69254 | -234.55970 | -234.416237 | -234.408945 | -234.408001 | -234.447855 | bond length of C=C: 1.3163 to 1.3382Å;
bond length of =C-C 1.5091 to 1.50714; bond length of C-C 1.5527 to 1.555; angle of =C-C-C: 111.642o to 112.642o |
The energy of the optimised structure from B3LYP/6-31G* calculation is a lot (1799 kcal/mol) higher than that from the HF/3-21G calculation. But the calculation method does not change the geometry of molecule much.
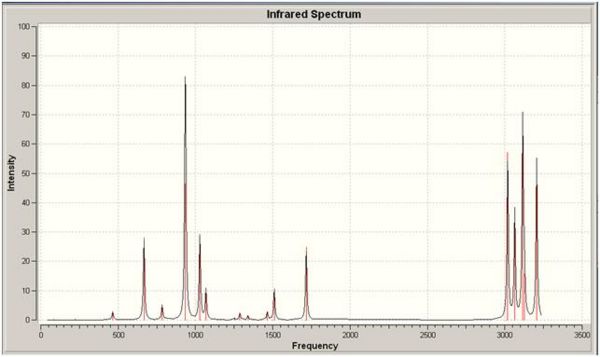
IR spectrum for the Ci anti 2 conformation
Optimizing the Chair and Boat Transition Structures
This pericylic reaction has been found to proceed with three possible transition states: loose boat, loose chair and a diradical tight-chair Delvar-type intermediate structure.
To generate the first transition state, an allyl fragment CH2CHCH2 was optimised, using HF/3-21G level of theory. This optimised fragment was then added on another window and the two fragments were oriented into a chair conformation. These two fragments was set to be 2.2Å apart. This overall molecule was then optimised and the frequencies were found, using the HF/3-21G theory. As this was a transition state, this molecule was optimised to a Berny transition state, with force constants calculated once and additional keyword Opt=NoEigen.
The optimised structure is shown below
| Chair Structure | Electronic energy (HF/3-21G) at 0 K | Sum of electronic and zero-point energies at 298.15 K(HF/3-21G) | Sum of electronic and thermal energies (HF-3-21G) | Electronic energy (B3LYP/6-31G*) | Sum of electronic and zero-point energies at 0 K (B3LYP/6-31G) | Sum of electronic and thermal energies at 298.15 K(B3LYP/6-31G) |
opt.JPG)
|
-231.619322 | -231.466701 | -231.461341 | -234.505427 | -234.362621 | -234.356705 |
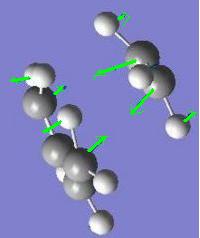
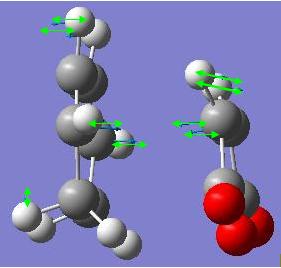
The frequency calculation gives an imaginary frequency of magnitude 817.954 cm-1 and the motion of vibration is shown below. This confirms that this was a transition state. This transition state has a C2h point group.
.JPG)
However, if the guessed transition structure is far from the exact structure, computing the force constant matrix may not produce the reaction coordinate as the curvature of the surface may be significantly different at points far removed from the transition structure. In some cases, a better transition structure can be generated by freezing the reaction coordinate.
The transition state is optimised (HF/3-21G) with two of the terminal carbons from the allyl fragments, which form/break a bond during the rearrangement, frozen to be 2.2Å.
The optimised structure looks very similar to the transition optimised in previous part, except the bond forming/breaking distances are fixed to 2.2 Å.
The bonds are then made unfrozen and optimised by using a normal guess Hessian modified to include the information about the two coordinates that we are differentiating along.
| Structure optimised by computing the force constants | Structure optimised by using the redundant coordinate editor | |
|---|---|---|
| Structure |
|
.JPG)
|
| Bond forming/bond breaking bond lengths (Å) | 2.02014, 2.02034 | 1.55081, 4.39027 |
The structures of the transition states optimised by two different methods looks quite different. The optimised structure by using the first method looks very similar to the guess chairtransition structure. The structure optimised by using the redundant coordinate editor looks very similar to the C2 Gauche 2 conformation.
The lengths of bond forming/breaking optimised by these two methods are very different.
Boat Transition State
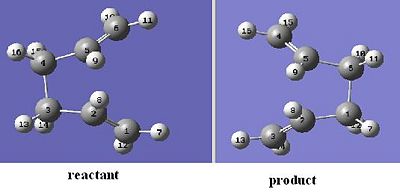
The optimised anti 2 structure was used to generate a boat transition state. This was done, by copying the optimised structure into a new molgroup, then adding another molecule to this molgroup. The result was in the form of two molecules in the same window. Using QST2 method can specify the reactants and products for a reaction and the calculation will interpolate between the two structures to try to find the transition state between them.
This calculation failed, as it produced a transition state reminicent of the previous chair conformation. This is because the program did not take the possible rotation about the bonds into account, it simply translated the allyl fragments.
To rectify this error, the rotation of the bonds was done for the program and the structures were cleaned, so that they are closer to the boat transition structure.
The QST2 calculation is then run again.
| Boat Structure | Electronic energy (HF/3-21G) at 0 K | Sum of electronic and zero-point energies(HF/3-21G) | Sum of electronic and thermal energies (HF-3-21G) | Electronic energy (B3LYP/6-31G*) | Sum of electronic and zero-point energies (B3LYP/6-31G) | Sum of electronic and thermal energies(B3LYP/6-31G) |
|
-231.602802 | -231.450929 | -231.445300 | -234.493065 | -234.351356 | -234.345053 |
The bond lengths were 1.381Å for the C-C bonds and the distance between the fragments is 2.14Å.
This transition state has C2v point group and -231.6028a.u. of energy. This is certainly a transition state, as it has a negative vibrational frequency at -839.959cm-1. The animated vibration shows the fragments approaching each other.
IRC
The optimised transition states were then used to perform a further calculation, the IRC (intrinsic reaction coordinate), to be able to follow the reaction path. This is done, by taking a set number of steps (initially set at 100) in the forward direction. The IRC function optimises the structure at each step of the reaction. The calculation is usually performed in both directions, however this reaction is symmetrical, so only the foward direction is needed. This was done, by using the HF method and the 3-21G basis set.
Once the calculation was completed, the output was checked to make sure that the actual energy minimum had been reached. If not,the lowest energy conformer should be selected and then optimised again.
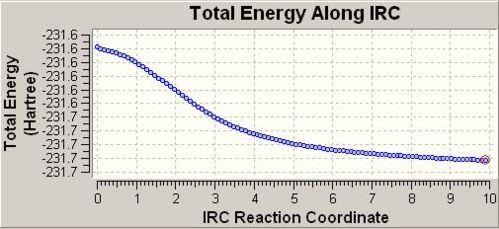
The boat IRC was set to 100 maxcycles. The following plot was given.
The anti 2 conformer undergoes sigmatropic rearrangement, via the boat transition state.
| Structure- anti 2 | Electronic energy (HF/3-21G) at 0 K | Sum of electronic and zero-point energies at 298.15 K(HF/3-21G) | Sum of electronic and thermal energies (HF-3-21G) | Electronic energy (B3LYP/6-31G*) | Sum of electronic and zero-point energies at 0 K (B3LYP/6-31G) | Sum of electronic and thermal energies at 298.15 K(B3LYP/6-31G) |
|
|
-231.69254 | -234.55970 | -234.416237 | -234.408945 | -234.408001 | -234.447855 |
The chair transition state was then calculated using the same method as for boat transition state.
In order to obtain the activation energies for the reaction via both transition structures, the chair and boat transition structures will have to be reoptimised using the B3LYP/6-31G* level of theory and the frequency calculations have to be carried out.
| HF/3-21G | B3LYP/6-31G* | Expt. | |
| at 298.15K | at 298.15 K | at 0K | |
| ΔE (Chair) | 45.94 | 34.056 | 33.5 ± 0.5 |
| ΔE (Boat) | 56.311 | 52.79 | 44.7 ± 2.0 |
References
1. Shogo Sakai, J. Mole Str: THEOCHEM., 583, (2002), p181-188
The Diels-Alder Cylcoaddition
This Diels Alder reaction is a concerted pericyclic reaction, involving 6п electrons, which means this will have a Hueckel transition state with suprafacial components.
If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed. The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden.
The Reactant Molecule: Cis-butadiene
The molecular orbitals of cis-butadiene were calulated and then the HOMO and LUMO orbitals were visualised to explain the approach the diene takes when the two molecules react. This helps to determine the transition state.
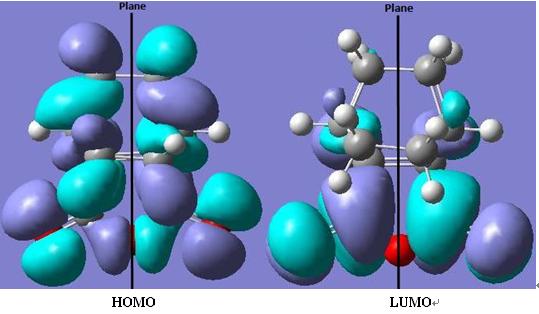
The HOMO of cis-butadiene is asymmetric (a) with respect to the plane of symmetry.
The LUMO of cis-butadiene is symmetric (s) with respect to the plane of symmetry.
The Reactant Molecule: Ethene Molecular
As seen, the symmetries of the HOMO/LUMO are the same, so that the reaction between the two molecules can proceed in a stereospecific and concerted fashion.
The LUMO of ethene is symmetric (s) with respect to the plane of symmetry.
The endo product is favoured with respect to the exo product, because the secondary orbital overlap of the endo is more favourable.
Generation of the Transition State
The possible transition states must be compared and analysed first. They must have the right approach to allow orbital approach and not too high in energy.
The transition state can be generated by optimising the two reactants separately and copy/paste them into a same window and orienting them into an enevelope-type structure. This is then optimised using HF/3-21G theory.
To find out whether this is a transition state or not, vibrational calculation of the optimised molecule shoule be done. As confirmed in the previous studies, the transition states should have imaginary frequencies. The imaginary vibration shows the motion the molecules undergo the approach to form the bonds.
HF/3-21G was used and a Berny transition state was generated, additional keywords opt=noeigen is needed for frequency calculations. The distance between the fragments was set to 2.3 angstroms and the molecule was optimised.
The interfragment distance is 2.21Å, which is the same the literature value. The dashed bond length is 1.39Å, which is closer to 1.34Å for a double bond than 1.54Å for a single bond. The other double bonds are also longer than the usual at 1.37Å. The ethene portion has a bond length of 1.375Å. All these show that these are in the process from double to single bond.
The negative vibrational frequency at -839.434cm-1 also indicates the transition state, that shows the motion of the two fragments approaching. The next frequency is at 269.039cm-1, corresponds to the ethene moving towards cis-butadiene.
The van der Waal radius of carbon is 1.70pm and the distance between the fragment is 2.21Å. This clearly shows that there is overlap between the adjacent carbon atoms on the fragments, which confirms that this is a transition state.
| Bond | Bond length/Å |
| sp2C=sp2C | 1.31605 |
| sp2C-sp3C | 1.50951 |
| sp3C-sp3C | 1.54644 |
Reference
1. Joey W. Storer, Laura Raimondi and K. N. Houk, J. Am. Chem. Soc., 1994, 116 (21), 9675-9683
2. Shogo Sakai, J. Phys. Chem. A, 2000, 104 (5), 922-927
Study of the Regioselectivity of the Diels-Alder Reaction
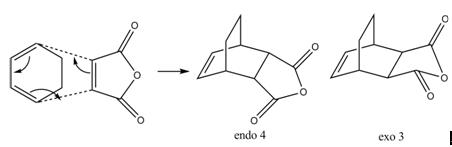
There are two possible products in this reaction, exo 3 and endo 4. The reaction is supposed to be kinetically controlled, so the endo 4 that is most likely to form. The endo transition state is then assumed to have a lower energy than the exo transition state, as relevant orbitals that leads to endo 4 overlap well with correct orientation.
The guess structure of transition state was computed. But the distance between two fragments are not known. In order to have a structure close to the exact structure, the fragments are first generated by feezing the reaction coordinate and minimizing the rest of the structure. The reaction coordiate is unforzen then when the molecule is fully relaxed and the transition state optimization is started again.
exo product
The sigma bond that joined the two reacants has a bond length of 1.57Å and the transition state has an energy of -606.90823901 a.u.
The vibrational analysis confirms this is a transition state as one negative frequency is observed at -647.45cm-1.
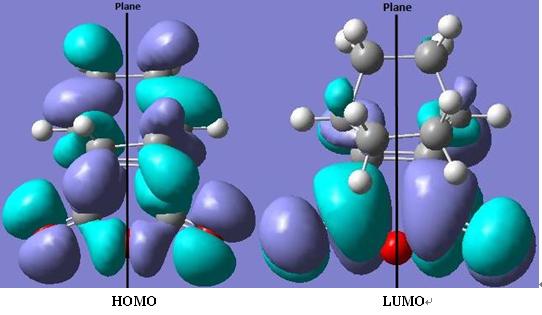
As seen from the HOMO of transition state molecule, there are many node planes, so it must be quite high in energy. This confirms the initial statement about exo transition state.
Endo product
The endo transition state cacn be optimised in the similar as exo product.-606.90823901 a.u. The sigma bond that joined the two reacants has a bond length of 1.568Å which is shorter than in exo product.
When comparing HOMOs from two molecules, it is clear to see the the endo transition state overlaps better and is thermodynamically more stable. The reason is the appearance of the second orbital interactions.