Rep:Mod:az916
Day 1
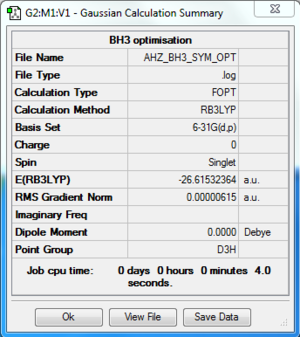
BH3
Computation method: RB3LYP/6-31G(d.p)
Summary table
Item table
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000049 0.001800 YES
RMS Displacement 0.000032 0.001200 YES
Predicted change in Energy=-8.985249D-10
Optimization completed.
-- Stationary point found.
Frequency analysis log File
6-31G(d.p) BH3 frequency log file
Low Frequency Lines
Low frequencies --- -0.6235 -0.3404 -0.0053 14.5386 17.7840 17.7950 Low frequencies --- 1163.0535 1213.2211 1213.2238
jmol Image
BH3 |
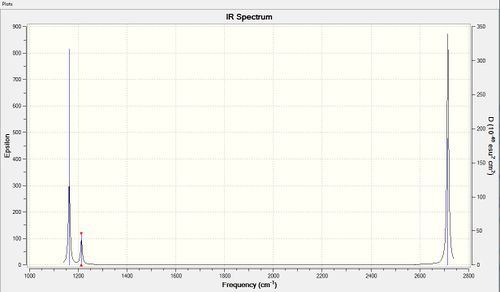
Vibrational spectrum for BH3
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 93 | A2 | yes | out-of-plane bend |
| 1213 | 14 | E' | very slight | bend |
| 1213 | 14 | E' | very slight | bend |
| 2582 | 0 | A1' | no | symmetric stretch |
| 2715 | 126 | A1' | yes | asymmetric stretch |
| 2715 | 126 | E' | no | asymmetric stretch |
BH3 has 6 calculated modes of vibration. However, in the spectrum above, only 3 peaks are observed. At 1213 cm-1 and 2715-1 there are in fact two pairs of degenerate vibration modes. Since the vibrations have the same energy, they occur at the same wavenumber (E=hc/λ). Stretching is higher in energy relative to bond deformation, resulting in the stretching peak occuring at a much higher frequency. The vibration at 2582 does not produce any signal in the spectrum as it is totally symmetric. A change in dipole is required to absorb IR radiation and produce a peak, thus a totally symmetric vibration will not result in radiation absorption.
Molecular orbitals of BH3

Both LCAO and 'real' MO approaches produce orbitals of the same symmetry and phases. The LCAO molecular orbitals are qualitatively determined by combining orbitals of similar energy and particular symmetries. The real MOs are likely to combine more atomic orbitals than LCAO predicts. Since electron-electron repulsion is also considered, it more predicts the distribution of electron density. MOs are therefore more spread out over the entire molecule.
Qualitative MO theory is likely adequate for predicting the general shapes and phases of orbitals in simple systems, but a computational approach is much more accurate for more complicated ones.
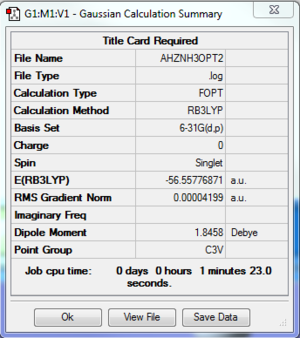
NH3
Computation method: RB3LYP/6-31G(d.p)
Summary table
Item table
Item Value Threshold Converged?
Maximum Force 0.000092 0.000450 YES
RMS Force 0.000039 0.000300 YES
Maximum Displacement 0.000305 0.001800 YES
RMS Displacement 0.000102 0.001200 YES
Predicted change in Energy=-1.875177D-08
Optimization completed.
-- Stationary point found.
Frequency analysis log File
6-31G(d.p) NH3 frequency log file
Low Frequency Lines
Low frequencies --- -32.4235 -32.4224 -11.4276 -0.0044 0.0115 0.0476 Low frequencies --- 1088.7628 1694.0251 1694.0251
jmol Image
NH3 |
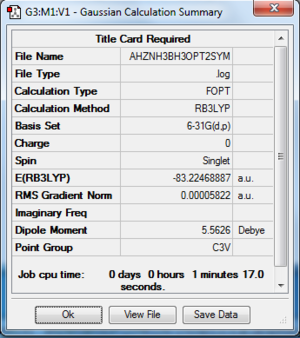
NH3BH3
Computation method: RB3LYP/6-31G(d.p)
Summary table
Item table
Item Value Threshold Converged?
Maximum Force 0.000137 0.000450 YES
RMS Force 0.000038 0.000300 YES
Maximum Displacement 0.000766 0.001800 YES
RMS Displacement 0.000181 0.001200 YES
Predicted change in Energy=-1.139042D-07
Optimization completed.
-- Stationary point found.
Frequency analysis log File
6-31G(d.p) NH3BH3 frequency log file
Low Frequency Lines
Low frequencies --- -32.4235 -32.4224 -11.4276 -0.0044 0.0115 0.0476 Low frequencies --- 1088.7628 1694.0251 1694.0251
jmol Image
NH3BH3 |
Bond strength and energy discussion
The energy of the N-B bond in ammonia borane can be calculated by subracting the total energy of ammonia and borane from the energy of NH3BH3:
- E(NH3)= -56.55776871 a.u
- E(BH3)= -26.61532364 a.u.
- E(NH3BH3)= -83.22468887 a.u.
- ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = (-83.22468887)-[(-56.55776871)+(-26.61532364)] = -0.05159652 a.u.≈ 135 KJ.mol-1
The bond energy obtained of 135 KJ.mol-1 aligns well with the literature value of ~130 KJ.mol-1[2]
The dative bond is of medium strength. An ordinary covalent bond such as N-H has a dissociation enthalphy of 386 KJ.mol[3]. It is still much larger than weak dipole interactions such as hydrogen bonds at around 2-5 KJ.mol-1[4].
Smf115 (talk) 16:00, 28 May 2018 (BST)Correct calculation method, just be aware of the accuracy of energy values when reporting the molecules energies in a.u. Nice referenced comparisons to evaluate the bond strength.
BBr3
Computation method: B3LYP/6-31G(d,p)LANL2DZ
Completed frequency file D-Space link
http://hdl.handle.net/10042/202445
Summary table
Item table
Item Value Threshold Converged?
Maximum Force 0.000025 0.000450 YES
RMS Force 0.000015 0.000300 YES
Maximum Displacement 0.000122 0.001800 YES
RMS Displacement 0.000069 0.001200 YES
Predicted change in Energy=-3.491783D-09
Optimization completed.
-- Stationary point found.
Frequency analysis log File
6-31G(d.p) BBr3 frequency log file
Low Frequency Lines
Low frequencies --- -4.0153 -0.0002 0.0000 0.0001 1.7448 3.4070 Low frequencies --- 155.8881 155.9561 267.7048
jmol Image
BBr3 |
Project: Aromaticity
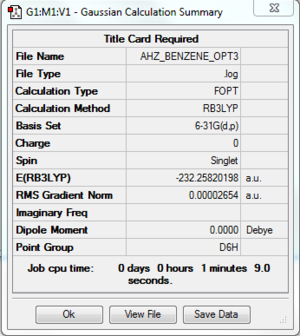
Benzene
Computation method: RB3LYP/6-31G(d.p)
Summary table
Item table
Item Value Threshold Converged?
Maximum Force 0.000045 0.000450 YES
RMS Force 0.000016 0.000300 YES
Maximum Displacement 0.000097 0.001800 YES
RMS Displacement 0.000036 0.001200 YES
Predicted change in Energy=-1.579511D-08
Optimization completed.
-- Stationary point found.
Frequency analysis log File
6-31G(d.p) benzene frequency log file
Low Frequency Lines
Low frequencies --- -0.0088 -0.0041 -0.0041 12.5838 12.5838 16.4940 Low frequencies --- 414.3526 414.3526 621.2606
jmol Image
benzene |
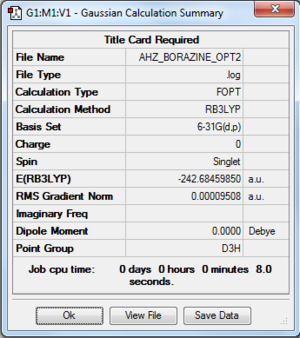
Borazine
Computation method: RB3LYP/6-31G(d.p)
Summary table
Item table
Item Value Threshold Converged?
Maximum Force 0.000111 0.000450 YES
RMS Force 0.000046 0.000300 YES
Maximum Displacement 0.000380 0.001800 YES
RMS Displacement 0.000097 0.001200 YES
Predicted change in Energy=-1.890893D-07
Optimization completed.
-- Stationary point found.
Frequency analysis log File
6-31G(d.p) borazine frequency log file
Low Frequency Lines
Low frequencies --- -6.0214 -5.8056 -5.2959 -0.0106 0.0584 0.1775 Low frequencies --- 289.2503 289.2583 403.8913
jmol Image
borazine |
Charge Distribution Comparison
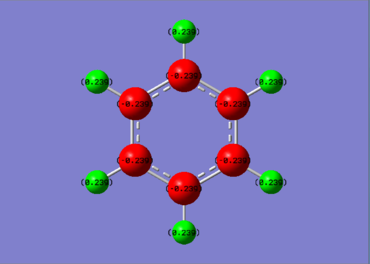 |
 |
In benzene, carbon is slightly more electronegative than hydrogen (2.55 vs 2.20[5]), thus carbon holds more negative charge than hydrogen. The charge on carbon is -0.239, whilst hydrogen has a charge of 0.239. Due to the symmetry of benzene, there is no overall dipole, however. There must be an asymmetric charge distribution over the length of a molecule to cause a net dipole moment. Any vector drawn from a negatively charged to positively charged area of the molecule is cancelled by an opposing vector mirrored through the inversion center.
Borazine on the other hand has a significantly different charge distribution. Nitrogen is significantly more electronegative than boron (3.04 vs 2.04[5]), and a large charge disparity results. The hydrogens bonded to boron are very slightly negative (-0.077) whilst those bonded to nitrogen are relatively positive (0.432). Unlike benzene, borazine does not have a center of inversion. As a result, the molecule possesses a net dipole moment. Each boron is opposing a nitrogen in the ring, so a vector from negative to positive charge can be drawn accross the molecule.
Orbital Comparison
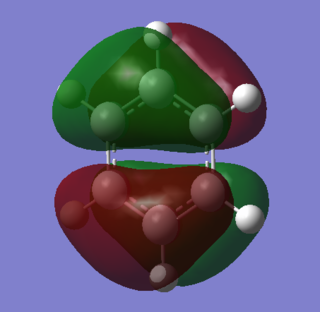 |
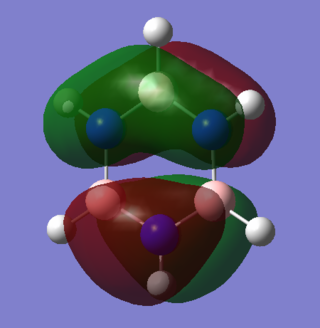 |
Both orbitals consist of two sets of pi systems separated by a nodal plane. In benzene, the MO still has an ungerade center of inversion as the shapes of the pi systems are identical on both sides of the molecule. In borazine, however, there is distortion of the orbitals due to a net dipole in the molecule. Nitrogen's electronegativity withdraws electron density in this predominantly bonding orbital. The upper system contains 2 nitrogen atoms which reduce the orbital size around boron. This is espeically pronounced in the lower system, where the orbital boundary surface does not completely cover the two boron atoms adjacent to the nitrogen.
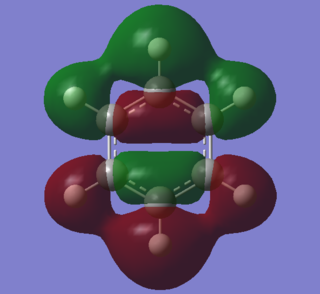 |
 |
Two comparable sigma bonding molecular orbitals are pictured above. The benzene one is slightly anti-bonding in character abd both have 3 nodes. Despite consisting of equivalent atomic orbitals, the benzene MO is very dissimilar to the borazine one. In benzene, the MO has an ungerade center of inversion as electron density distribution in the upper and lower systems is the same. In borazine, the nitrogen in the lower system skews the atomic p orbitals in the plane of the ring so that there are no longer any nodes through bonds in the molecule. The ordering of this MO in borazine is 13, whilst in benzene it is 16. Part of the reason for this significant difference in energy ordering may be due to this lack of nodal plane through bonds. Repulsion between atoms could be slightly reduced, rendering this MO more stable in relative terms to the benzene counterpart.
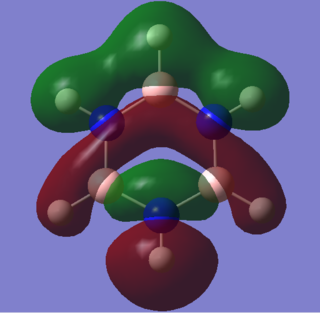
 |
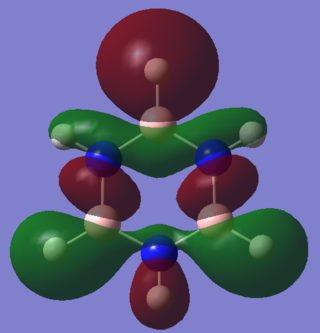 |
These comparable sigma slightly anti-bonding MOs exhibit significant differences in lobe size due to dipole moment disparaties. There are 4 nodal planes in both MOs, and the benzene MO is gerade with respect to inversion. Benzene has no dipole moment, so the s lobes on the two hydrogens at the top and bottom of the molecule are of equal size. In contrast, the hydrogen lobe bonded to boron is much larger than that bonded to nitrogen. As identified int the charge distribution analysis, this N-H hydrogen is slightly positive whilst the B-H one is slightly negative. This causes the large disparity in lobe size. The Hydrogens bonded to the borons adjacent to the lower nitrogen also have a large degree of electron density relative to the comparable ones on benzene.
Smf115 (talk) 13:34, 1 June 2018 (BST)A very good range of MOs chosen with MO 16 and 13 particularly interesting. Good comparison of the MOs with good symmetry details such as the inversion centre.
Aromaticity Comparison
Aromaticity is typically defined using Hückel's rules:
- The molecule must be cyclic and planar
- The molecule must have 4n+2 π electrons
- The π orbitals must be contiguous in the ring
Whilst this definition is adequate in many cases, a molecular orbital approach reveals greater insight than this qualitative definition. Aromaticity as a general concept imparts stability to cyclic molecules through resonance. This can be applied to molecules that are not planar, and extends beyond π orbitals exclusively [6]. σ MOs can also be delocalised, imparting stability by diffusing electron density. Both of these factors must be considered in discussing the extent of aromaticity.
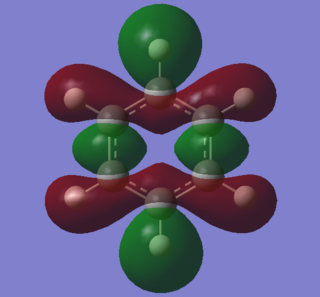
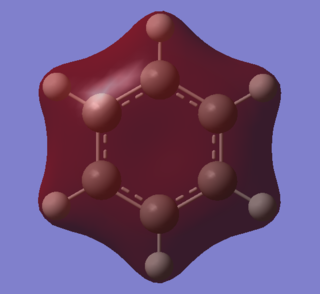 |
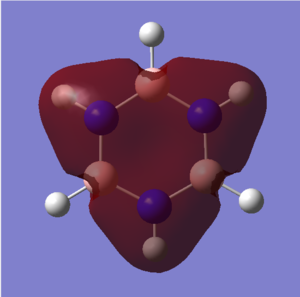 |
A characteristic feature of aromatic systems is an intermediate bond length relative to the equivalent alkene. This effect is often attributed to overlap of p orbitals, but literature indicates that it is sigma orbitals which predominantly delocalise, forcing pi electrons to then delocalise as symmetry is increased[7]. The sigma element of aromaticty is evident in these orbitals. Both consist of bonding s orbitals of one phase. The benzene orbital has higher symmetry than the borazine one, owing to an equal charge distribution across each carbon in the ring. Electron density is concentrated around the nitrogen atoms in borazine, resulting in lower resonance stability. Symmetry can be used to indicate aromatic stability. The benzene orbital has D6 symmetry whilst the borazine one has D3h symmetry. This lower symmetry aligns with lower resonance stability.
 |
 |
Both orbitals pictures also display delocalised sigma bonding frameworks. The MOs are likely to be less of a contributing factor to aromaticity than benzene and borazine orbital 7, since the MOs contain a node and are not distributed over the entire molecule. Given that two sigma MOs in each molecule contribute to delocalisation relative to only one pi MO, it is likely that sigma bonding has a greater impact on delocalisation as previously stated in literature. The borazine MO in this case has distorted electron distribution with a higher density around nitrogen, likely resulting in less delocalisation and stability. The phase formed of p orbitals in the ring's plane pointing towards the center is likely to be the predominant factor in delocalisation. Since this ring is intact in borazine unlike the ring of s orbitals from hydrogen, the orbital will still contribute to delocalisation.
 |
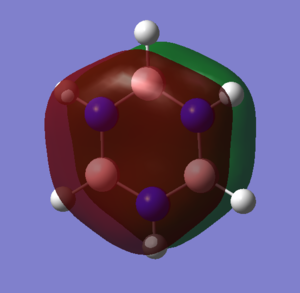 |
The two MOs pictured feature pz orbitals perpendicular to the ring plane. These are typically associated with aromaticity, but should not be considered in isolation. Electron density is again very symmetrically distributed in benzene, but distorted towards nitrogen in borazine. The distortion of all orbitals involved in aromaticity in borazine results in a lower degree of electron delocalisation and therefore lower resonance energy than benzene.
Smf115 (talk) 13:31, 1 June 2018 (BST)Well presented answer and excellent use of the MOs visualised to illustrate different concepts such as sigma-aromaticity. To improve, some more advanced concepts of aromaticity, contradictory examples or quantitative descriptions could have been discussed.
Smf115 (talk) 13:31, 1 June 2018 (BST)Overall, a great wiki report with an excellent first section.
- ↑ Hunt Research Group tutorial problem sheet, URL: http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf, Accessed: 22/05/2018
- ↑ Moury, R.; Demirci, U.B. Hydrazine Borane and Hydrazinidoboranes as Chemical Hydrogen Storage Materials. Energies 2015, 8, 3118-3141
- ↑ Wired Chemist, URL: http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html, Accessed: 22/05/2018
- ↑ Porter, T., Heim, G., & Kubiak, C. (2017). Effects of electron transfer on the stability of hydrogen bonds. Chemical Science., 8(11), 7324-7329.
- ↑ 5.0 5.1 A.L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215
- ↑ M. B. Smith, J. March, Marchs Advances Organic Chemistry, 5th Edition, Wiley, New York, 2001, p. 48
- ↑ Influence of .sigma. and .pi. electrons on aromaticity Karl Jug and Andreas M. Koester Journal of the American Chemical Society 1990 112 (19), 6772-6777 DOI: 10.1021/ja00175a005