Rep:Mod:awc106 module2
Module 2
Day 1
BH3
A molecule of BH3 was created in Gaussview. Below is the visual representation created by Gaussview:

The molecule was then optimised. This was done using the calculation tab in Gaussview. Certain commands were set in to the optimisation, these included the method, the basis set and what type of calculation to undertake. The method was set to BLYP, this method determines the type of approximations the program makes when solving the Schrodinger equation. The basis set was set to 3-21G. This basis set has a low accuracy, but this ensured that the calculations were quick to perform. Finally the calculation was set to OPT for an optimisation. Once complete, the following results summary was available:

The above summary tells us a great deal about the calculation and the molecule. Data on the bond distanced and angles can also be gleaned from gaussview, below is a summary of the results:
Table 1: BH3 Data | |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final Energy | -26.5a.u. |
| Gradient | 0.00000285a.u. |
| Dipole Moment | 0.00D |
| Point Group | D3h |
| Optimised B-H Distance | 1.19Å |
| Optimised B-H Angle | 120.0° |
| Calculation Time | 23s |
There is yet more information we can gain from this inital optimisation. Two plots have been created as part of the calculation. One a graph of total energy against optimisation step number, and the other of gradient against step number. The first graph shows the energy of the molecule at each step of the optimisation, thus the step with the lowest energy is the most stable form of the molecule.

As D_Space would not accept my file, I have linked it below:
BCl3
A molecule of BCl3 was created in Gaussview.
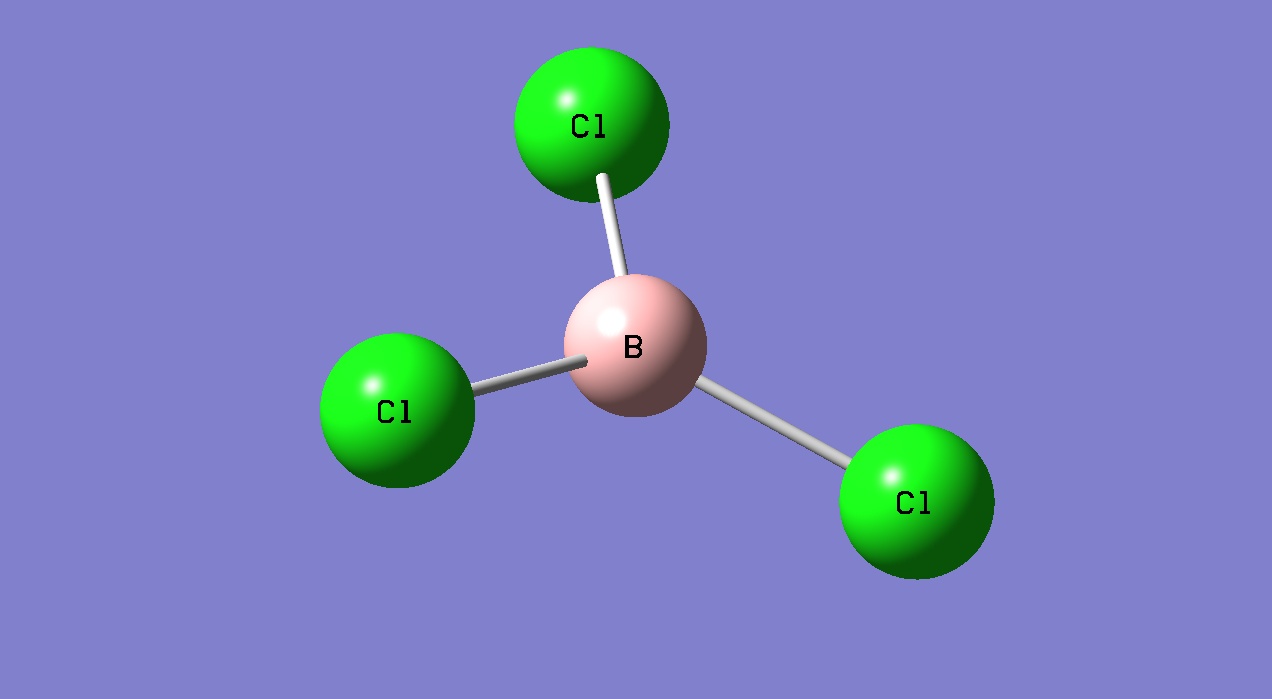
In this case the symmetry of the molecule was then restricted. The point group of the molecule was restricted to that of D3h, and the tolerance set to very tight (0.0001). Then an optimisation calculation was prepared. In this case the method was set to DFT B3LYP and the basis set used was LanL2MB. This is a lrger basis set than used for BH3, but is still only a medium level basis set. Again the following results summary was available:
Table 2: BCl3 Data | |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2MB |
| Final Energy | -69.4a.u. |
| Gradient | 0.00005905a.u. |
| Dipole Moment | 0.00D |
| Point Group | D3h |
| Optimised B-H Distance | 1.87Å |
| Optimised B-H Angle | 120.0° |
| Calculation Time | 10s |
As D_Space would not accept my file, I have linked it below:
SH2
The same proceedure was carried out for SH2 with the follwing results:

Table 3: SH2 Data | |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2MB |
| Final Energy | -11.3a.u. |
| Gradient | 0.00000119a.u. |
| Dipole Moment | 2.19D |
| Point Group | C2v |
| Optimised B-H Distance | 1.31Å |
| Optimised B-H Angle | 109.5° |
| Calculation Time | 18s |
The xyz cooridnates of the molecule (as stated in the log file) are:
Standard orientation: --------------------------------------------------------------------- Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z --------------------------------------------------------------------- 1 16 0 0.000000 0.000000 0.084007 2 1 0 0.000000 1.069800 -0.672054 3 1 0 0.000000 -1.069800 -0.672054
As D_Space would not accept my file, I have linked it below:
BH3 Vibrational and MO Analysis
So far we have effectively been caclulating the first derviatives of potential energy curves. However, whilst this process tells us the slope, it doesnt tell us if we have arrived at a maximum or a minimum energy. In this section, we will carry out a frequency analysis. This is essentially calculating the second derviative of the potential energy curve, and if we arrive at an answere where all of the frequencies are postitive then we have a minium, if one of the frequencies is negative then we have a transition state, and if more than one is negative then the optimisation has failed or finished incompletely. To carry out this analysis, instead of performing an optimisation, the job type in this case is set to frequency. Also we add the phrase "pop=(full,nbo)" to the additional keywords box in order to request a full analysis of the electron density and the molecular orbitals. This analysis resulted in the following results summary:

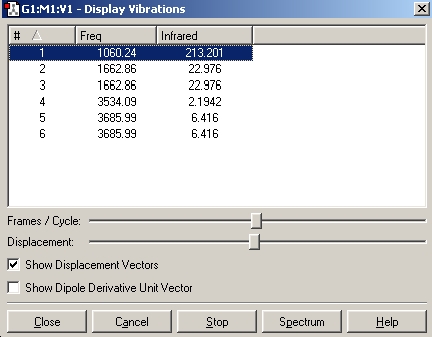
As can be seen, the total energy is exactly the same as our inital optimisation, this means that we have the exact same molecule and can continue with the analysis. Under the results tab, the vibrations option is now available. Once opened the follwing window becomes visible:

On inspecting the vibrational frequencies we can see that they all have a positive value, this means that we have indeed calculated the energy minima. ONe of the available options is the spectra of the molecule we have optimised, as such the IR spectra of BH3 can be seen below:

It is also possible to animate the various vibrational modes of the molecule, and as such inspect which frequency corresponds to which bending or stretching mode of the molecule.
Immediately we notice that there are clealy six vibrational modes of BH3, and yet there are not six peaks. This can be explained by the fact that some of the peaks are degenerate, i.e. there asymmetric and symmetric stretches and if there are two then they will not both be recognised as separate signals.
As I was unable to publish my files on D-Space, I have linked the file below:
https://www.ch.ic.ac.uk/wiki/images/c/c8/HCRAWFORD_BH3_FREQ.LOG.jpg
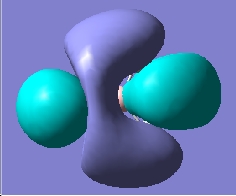
When we carry out calculations such as the ones performed above, we are solving the electronic structure of the molecule of interest, and thus we are able to obtain the molecular orbitals of molecules. It is also possible to theoretically predict the molecular orbitals of a molecule, and below is the molecular orbital diagram of BH3. We can use it make a comparison between the theoretically derived molecular orbitals, and those calculated by Gaussian.
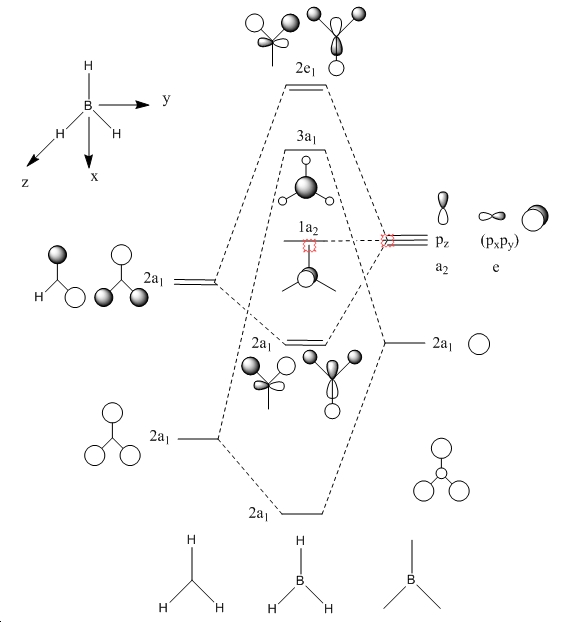
In order to calculate the MO's, the optimised structure was opened, and another calculation performed. In the additional keywords section was written "pop=full", this switched on the MO analysis. The file was run through Gaussian, and when complete, the MOs were available under the edit tab.
Table 5: BH3 MO Analysis | ||
| Orbital Number | Qualitative MO's | Quantitaive MOs |
| HOMO-3 | 
|

|
| HOMO-2 | 
|

|
| HOMO-1 | 
|

|
| HOMO | 
|

|
| LUMO | 
|

|
| LUMO+1 | 
|
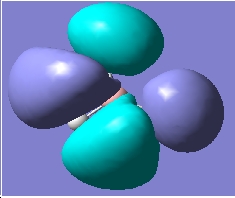
|
| LUMO+2 | 
|
|
As we can see, there is a a good agreement with the theoretically and computationally dervied orbitals. This tells us that qualitative MO theory is a very useful tool.
As I was unable to publish my files on D-Space, I have linked the file below:
https://www.ch.ic.ac.uk/wiki/images/a/a9/HCRAWFORD_BH3_MO.LOG.jpg
Day 2: Cis Trans Isomerism
Introduction
In this section we are going to carry out calculations on Mo(CO)4(Me3)2. We will use the calculations performed to predict the stability and spectral data of the two isomers, cis and trans. We will be able to use the CO vibrational bands to determine the symmetry of the two complexes. We expect four bands for the cis isomer, and one band for the trans isomer.
In order to achieve a good result, the optimisations were set up as follows. The cis and trans forms were drawn in ChemBio3D and saved as .gjf files and subsequently opened in Gaussview. A calculation was set up, using the B3LYP method, and a basis set of LANL2MB, with "opt=loose" written in the keywords section. This calculation was used to obtaine a rough initial geometry. The two calculations were sent to the SCAN service to run overnight. Once these calculations had finished, further calculations were run from the optimised geometries, this time using a higher basis set of LANL2DZ and "int=ultrafine scf=conver=9" in the keywords section which increased the electronic convergence. This is a higher basis set and pseudo-potential. These two calculations were again put on the SCAN service overnight.
Trans Mo(CO)4(Me3)2
Table 6: Trans Mo(CO)4(Me3)2 Optimisations | ||||||
| Optimisation | Results | Image | File | |||
| Initial | 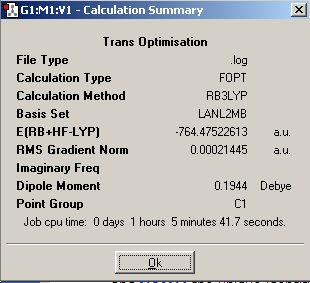
|
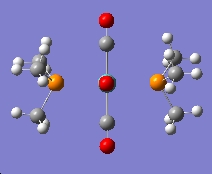
|
https://www.ch.ic.ac.uk/wiki/images/4/44/Trans_opt_initial.jpg | |||
| Ultrafine | 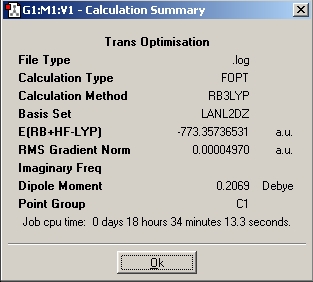
|
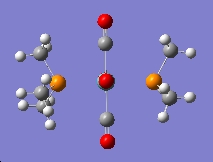
|
DOI:10042/to-1798 | |||
| Frequency | 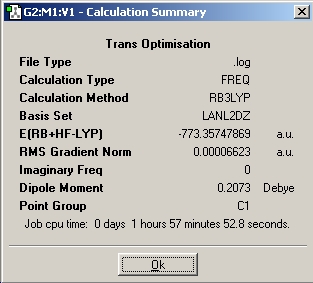
|
|
DOI:10042/to-1801 | |||
Cis Mo(CO)4(Me3)2
Table 7: Cis Mo(CO)4(Me3)2 Optimisations | ||||||
| Optimisation | Results | Image | File | |||
| Initial | 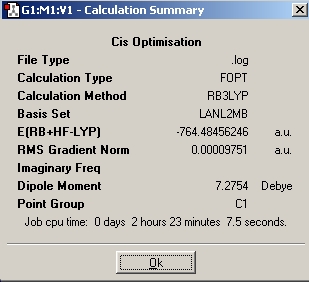
|
|
DOI:10042/to-1723 | |||
| Ultrafine | 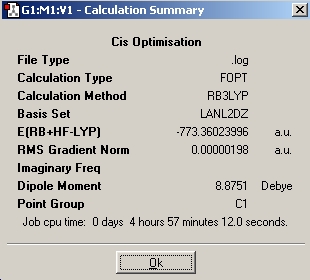
|
|
DOI:10042/to-1799 | |||
| Frequency | 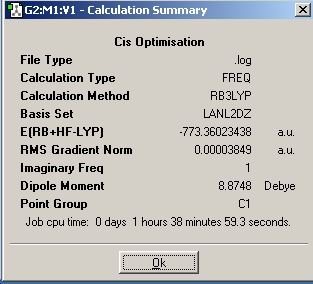
|
|
DOI:10042/to-1800 | |||
IR
Trans Spectra

Cis Spectra

Table 8: Mo(CO)4(Me3)2 IR Data | |||
| Trans Frequency/cm-1 | Trans Intensity | Cis Frequency/cm-1 | Cis Intensity |
| 1839.0 | 1999.0 | 1848.5 | 1068.8 |
| 1839.3 | 1999.8 | 1850.7 | 1960.9 |
| 1882.9 | 6.1 | 1869.9 | 666.3 |
| 1954.4 | 3.1 | 1960.4 | 321.7 |
As we can see the two spectra produced are very similar, and the data obtained agrees well with that given in the literature. We can also note that the cis isomer displays four peaks of alost equal intensity, compared with the trans which has two main peaks. This is due to the symmetry of the molecule.
From the information obtinaed, we can calculate the energy difference between the two isomers. We can see that the trans isomer is the more stable with the lower total energy. Can we imagine a scenario in which it was the cis isomer which was more stable? By fine-tuning the molecule, by altering the ligands, we can alter the relative ordering of the two isomers. We can see that the cis isomer is more sterically hindered, thus by reducing the steric bulk of the ligands we can imagine that the energy difference would decrease, and even the possibility of the cis isomer becoming the more stable.
Day 3: Ammonia
Initial Optimisation
In this part of the report we will be performing a similar range of calculations on the isomers of ammonia. The aim is to investigate the effect of symmetry on the structures, their energies, and the relative optimisation times. During the first optimisation, a molecule of NH3 was generated in Gaussview, and the basis set used was 6-31G and the method used was B3LYP. Then another molecule of NH3 was created and one bond was set to a length of 1.01Å, and the ignore symmetry option was invoked. FInally the nh3_b3lyp_d3h.txt provided was opened and an optimisation run. This file included a dummy atom which restricted the symmetry of the molecule.
Table 9: Initial Optimisation of NH3 | ||
| Optimisation | Results Summary | Image |
| Inital Optimisation | 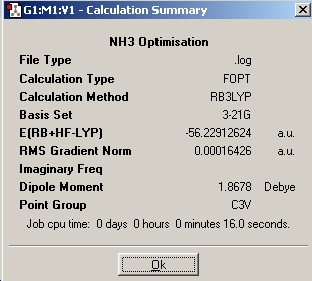
|
|
| Igmore Symmetry Optimisation | 
|
|
| Nh3_b3lyp_d3h Optimisation | 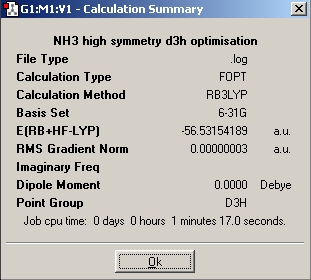
|

|
As I was unable to publish my output files on D-Space, I have linked the files below:
https://www.ch.ic.ac.uk/wiki/images/3/36/HCRAWFORD_NH3_OPT.jpg
https://www.ch.ic.ac.uk/wiki/images/6/61/HCRAWFORD_NH3_IGNORESYMMETRY_OPT.jpg
https://www.ch.ic.ac.uk/wiki/images/c/cc/Nh3_b3lyp_d3h.jpg
Higher Basis Set
The next step is to utilise a better method and basis set, and to examine the effect it has on the time taken to perform the calculation, the final geometry and energies that are obtained. The basis set used was 6-311+G(d,p) and the method used was MP2. Next the file nh3_mp2_d3h.txt was used and an optimisation run from it. These two calculations have achieved the optimisation of the ground state of NH3 with a point group symmetry of C3v and the inversion transition state, which is planar and has D3h symmetry.
Table 10: Optimisation of NH3 With Higher Basis Set | ||
| Optimisation | Results Summary | Image |
| Inital Optimisation | 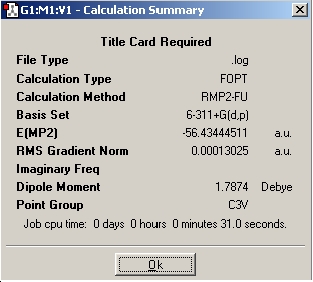
|
|
| Igmore Symmetry Optimisation | 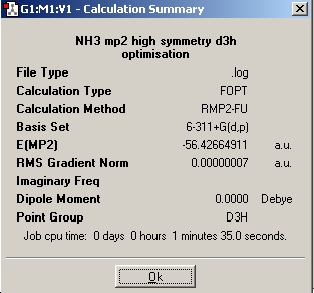
|

|
As I was unable to publish my output file on D-Space, I have linked the files below:
https://www.ch.ic.ac.uk/wiki/images/c/cc/HCRAWFORD_NH3_6-311_OPT.jpg
https://www.ch.ic.ac.uk/wiki/images/5/54/NH3_MP2_D3H.jpg
Looking at the two sets of optimisations we have just performed, we can see that the higher level MP2/6-311+G(d,p) calculations took longer to compute, approximately 15seconds longer in both cases. For the greater degree of accuracy acheived by using the higher basis set this time is acceptable, however with more complex molecules, the time difference would undoubtably be much larger.
We can also calculate ΔE=E(D3h)-E(C3v) for the two basis sets. For the B3LYP/6-31G we have an energy difference of 0.0078 a.u., and for the MP2/6-311+G(d,p) set of calculations we have -0.302 a.u. If we compare this to the experimentally determined difference of 24.3 kJ/mol, we see that whilst the higher basis set is mroe accuarate, is is not quite the same as that determined experimentally.
The Inversion Mechanism
So far we have optimised the ground state of NH3 with a point group symmetry of C3v and the inversion transition state, which is planar and has D3h symmetry. However we have not yet linked these two forms of ammonia together via a reaction pathway. Due to the shortcomings of Gaussview, a scan can not be performed. A scan varies one coordinate whilst the other coordinates optimises. In the case of ammonia, the nitrogen atom will remain stationary and the hydrogen atoms will move about it during optimisation. A scan file was provided. A scan calculation provides a graph of energy against scan step, which is a visualisation of the potential energy surface.

Under the results tab, the scan option is available. This provides a visualisation of the molecule at each scan step. Here is a summary:
Table 11: Summary of Scan Steps | ||
| Scan Step | Image | Maxima/Minima |
| 1 | 
|
Neither |
| 12 | 
|
Energy Minima |
| 21 | 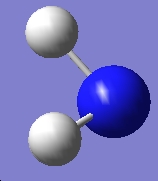
|
Energy Maxima |
Vibrational Analysis
In this section we will caclulate the vibrational spectrum of NH3 of both the ground state (C3v symmetry) and the planar inversion transition state (D3h symmetry). We will be using the optimised structures from the B3LYP/6-31G calculations.
C3v

D3h
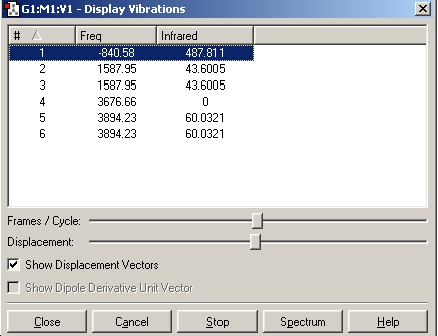
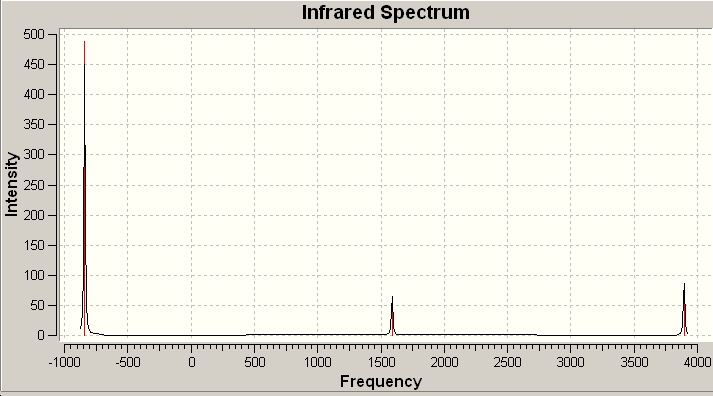
Table 12: Comparison of Vibrational Modes | |||
| Vibration Number | C3v | D3h | |
| 1 | 
|
| |
| 2 | 
|
| |
| 3 | 
|

| |
| 4 | 
|
| |
| 5 | 
|
| |
| 6 | 
|

| |
As can be seen from the above results, in the case of the C3v structure all of the frequencies are positive, this tells us that we have the minimised structure. Compared with the D3h structure which has one negative frequency (-840.58). This tells us that thi structure is a transition state. When we examine the table of the vibrational modes, we can see that all of the vibrational modes match up to one another. We can also see that vibrational mode 1 follows the inversion pathway.
As I was unable to publish my results on D-Space, I have linked the files below:
https://www.ch.ic.ac.uk/wiki/images/3/3b/57bjjd8d8djhpoodjdu88sjs7e3pic.jpg
https://www.ch.ic.ac.uk/wiki/images/f/f6/57bjjd8d8djhdweejdu88sjs7e3pic.jpg
Mini Project: Ammonia-Borane
Ammonia borane NH3BH3 is a Lewis acid-base pair molecule. NH3BH3 is also under scrutiny as a very promising molecule for the storage of hydrogen to be used as a new fuel. Ammonia-borane is 19.6% by weight hydrogen.
In this part of the report the first optimisation, molecules of NH3BH3(staggered and eclipsed) were generated in Gaussview, and then optimisations run using a basis set of 6-31G and the method used was B3LYP. The next step was to utilise a better method and basis set, the basis set used was 6-311+G(d,p) and the method used was MP2. Finally the keywords "pop=full" were included in the optimisation, and the checkpoint file examined in order to inspect the molecular orbitals of the different conformations.
Ammonia Borane
Table 13: NH3BH3 | |||||||||||
| Staggered | Eclipsed | ||||||||||
| Results | Image | HOMO | Results | Image | HOMO | ||||||
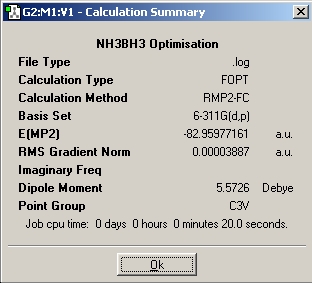
|
|
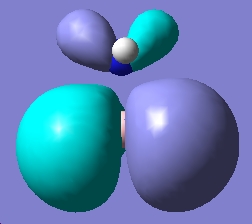
|
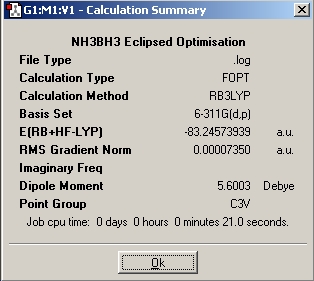
|
|

| ||||||
| https://www.ch.ic.ac.uk/wiki/images/e/e7/AB_1.log | https://www.ch.ic.ac.uk/wiki/images/b/b4/AB_2.log | ||||||||||
Upon examining the results obtained, we can clearly see that there is not a great difference in energy between the staggered and eclipsed conformations. We would expect however that the staggered conformation wold be lower in energy due to reduced steric hindrance of the neighboring groups.
Ethane
Ammonia-borane is isoelectronic with ethane. It is thus beneficial to compare the two molecules. The same set of calculations used for ammonia-borane were repeated for ethane.
Table 14: Ethane | |||||||||||
| Staggered | Eclipsed | ||||||||||
| Results | Image | HOMO | Results | Image | HOMO | ||||||
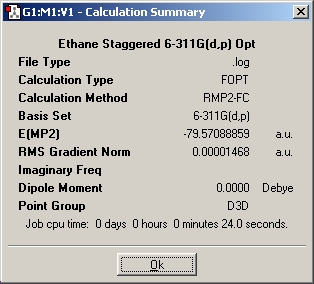
|
|

|
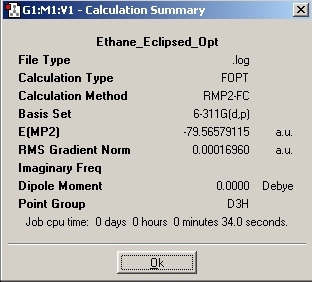
|
|

| ||||||
| https://www.ch.ic.ac.uk/wiki/images/3/38/Ethane.log | https://www.ch.ic.ac.uk/wiki/images/4/4c/Ethane_2.log | ||||||||||
Here again we can see that there is not a large energy difference between the two conformations, we know however that it is the staggered conformation which is the energy minima. We can see however, in comparison of the two sets of calculation, that the two sets of energy differences are both very small.
Reaction
It is also beneficial to determine the stability of NH3BH3 relative to its precursors. NH3BH3 is synthesised according to the following scheme[1]:
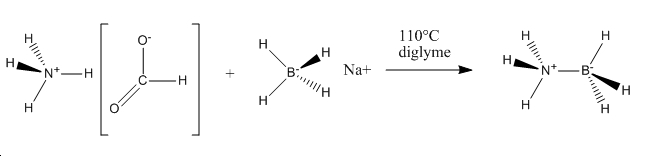
Hydrogen (H2) is then released resulting in NH3BH3. Therefore we can compare the relative energies of the reactants and products and calculate E(reactants)-E(products).
Table 15: Products and Reactants | ||
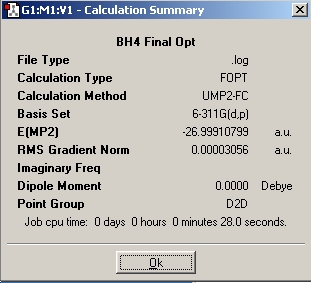
| NH4+ | BH4- | NH3BH3 |

|
|

|

|
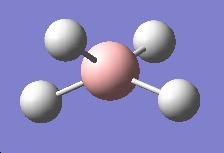
|
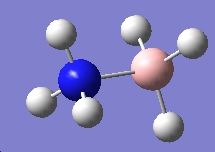
|
| https://www.ch.ic.ac.uk/wiki/images/1/1e/NH4.log | https://www.ch.ic.ac.uk/wiki/images/0/0f/BH4.log | https://www.ch.ic.ac.uk/wiki/images/d/db/NH3BH3.log |
We can calculate E(reactants)-E(products) from this information. Performing this calculation, we arrive at a value of -0.79a.u. This tells us that ammonia-borane is more stable relative to its reactants, which means that it is the thermodynamic product of the reaction between sodium borohydride and ammonium chloride.
By-Products
As can be seen from the below scheme, the dehydrogenation of NH3BH3 results in several by-products[2].
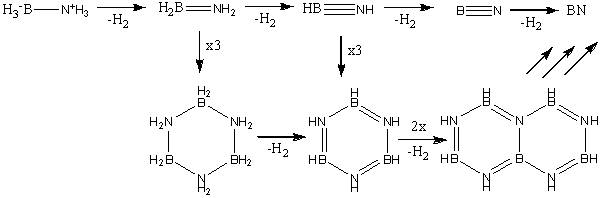
It is important to investigate these potential products, as if ammonia-borane does become a future fuel, it will be necessary to do something with the by-products, either t recycle them, or to reuse them somewhere else. For example the cyclohexane-like product has the potential to poison fuel cell catalysts, and therefore it must be effectively removed so that it does not accumulate in the system [2].
Again calculations were performed, first using a basis set of 6-31G and a method of B3LYP. The next step was to utilise a better method and basis set, the basis set used was 6-311+G(d,p) and the method used was MP2.
Table 16: By-Products | ||
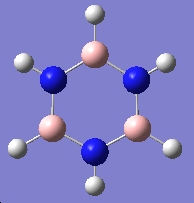
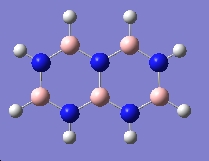
| Trimer | Borazine | Di-Borazine |
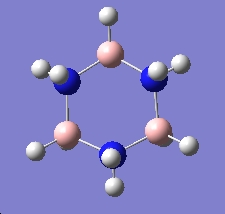
|
|
|
| -246.19 a.u. | -242.65 a.u. | -403.26 a.u. |
| C3v | D3h | C2v |
| https://www.ch.ic.ac.uk/wiki/images/3/35/Trimer.log | https://www.ch.ic.ac.uk/wiki/images/9/9c/Borazine.log | https://www.ch.ic.ac.uk/wiki/images/2/20/Di-borazine.log |
Again we can compare these with the corresponsing carbon analogues:
Table 17: Carbon Analogues | ||
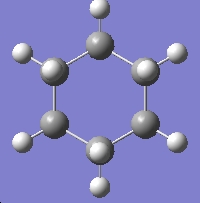
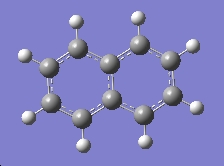
| Cyclohexane | Benzene | Naphthalene |
|

|
|
| -235.74 a.u. | -232.21 a.u. | -385.83 a.u. |
| D3d | D6h | D2h |
| https://www.ch.ic.ac.uk/wiki/images/d/d6/Cyclohexane.log | https://www.ch.ic.ac.uk/wiki/images/2/22/Benzene.log | https://www.ch.ic.ac.uk/wiki/images/8/84/Napthalene.log |
On first inspection we can see that the borane/nitrogen analogues appear to be the more stable molecules It also appears that the benzene and borazine molecules are less stable than their corresponding non-aromatic counter-parts. We know this to be the other way round, benzene has a far greater stability compared with cyclohexane conferred by the delocalisation of pi electrons across the whole molecule and we can infer that borazine would have a similar aromatic stability. This shows the limitations of some of the calculations that we have been performing, in that they are producing results that we know to be wrong. However we can see the napthalene type molecules have a far greater stability than the singly aromatic rings, and this is in line with what we would expect.
- ↑ Frances H. Stephens, Tom Baker, Myrna H. Matus, Daniel J. Grant, David A. Dixon; Angewandte Chemie International Edition, 2007. DOI:10.1002/anie.200603285
- ↑ 2.0 2.1 T. Marder; Angewandte Chemie International Edition, 2007, 46, 8116. DOI:10.1002/anie.200703150
Awc106 15:53, 17 February 2009 (UTC)






