Rep:Mod:awc106 module1

Module 1: Structure and Spectroscopy

Introduction

Thanks to technological advances it is possible to model a wide variety of organic chemistry, including structure, reactivity and the outcomes of reactions using various programs that are widely available. In this module the main programs that will be used will be ChemBio3D and GaussView. ChemBio3D can be used to run a molecular mechanics (MM)calculaton which will give an output of energy (kcal/mol) with a breakdown including energy values corresponding to dipole-dipole, stretching, bending etc.

The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene will dimerise to produce one of two species, an exo or endo isomer. The dimerisation results specifically in the endo dimer, i.e. species 2 shown below, with species i being the exo dimer.

It is possible to hydrogenate the dimer. Hydrogenation of the endo dimer results in one of two possible hydro deriviatives (species 3 and 4 below), and upon prolonged hydrogenation the tetrahydro product is formed.

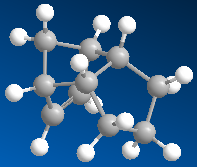
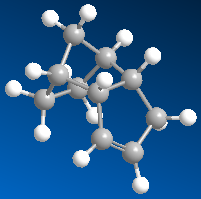
Running an MM2 calculation in ChemBio3D on the two isomers will calculate the relactive energies of the two forms of the dimer. Using the data obtained from the calculations performed, it will be possible to determine whether the dimerisation is under kinetic or thermodynamic control. In order to run an MM2 calculation the specific molecules are drawn in a chemdraw format, which are converted into 3-dimensional structures, and then the MM2 calculation can be run. The results of running the calculations can be seen in table 1.

Table 1:Dimers and Hydrogenated forms and their Relative Energies
Exo Dimer	Endo Dimer	Hydrogenated Species 1	Hydrogenated Species 2
31.88 kcal/mol	34.02 kcal/mol	35.93 kcal/mol	31.15 kcal/mol

Discussion

We are told that the dimerisation of cyclopenatdiene results specificslly in the endo isomer. This doesn't seem unreasonable, untill we look at the calculated energies. The MM2 calculations tell us that it should be the exo isomer being formed, as this has the lower energy, 31.88 kcal/mol c.f. 34.02kcal/mol for the endo isomer. This is a not insignificant energy difference of 2.14kcal/mol. This observation agrees with what we would expect when examining the two molecules. We would epect the exo dimer to be the most stable because of its staggered (rather than eclipsed) confomration. The fact that it is in fact the endo dimer which predominates leads us to the conclusion that the dimerisation is under kinetic control, rather than thermodynamic control, i.e. the isomer that is the most easily formed (that with the lowest activation energy) is the isomer that predominates, rather than the most stable. This infers that the endo dimer has the most stable transition state. However how can we explain these observations quantitatively? If we examine the breakdown of the energy readout for the two isomers we can gain some extra information.

Exo Dimer:

 Stretch:          1.2923
 Bend:            20.5870
 Stretch-Bend:    -0.8413
 Torsion:          7.6715
 Non-1,4 VDW:     -1.4358
 1,4 VDW:          4.2320
 Dipole/Dipole:    0.3778
 Total Energy:      31.8834 kcal/mol

Endo Dimer:

 Stretch:          1.2454
 Bend:            20.8603
 Stretch-Bend:    -0.8320
 Torsion:          9.5039
 Non-1,4 VDW:     -1.5083
 1,4 VDW:          4.3012
 Dipole/Dipole:    0.4448
 Total Energy:      34.0153 kcal/mol

Here we can see that the main differnce between the two isomers liesin the torsional strain energy. We can identify this as the strain at the newly formed carbon-carbon bond present in the dimer, which is greater in the endo form than the exo, this agrees with the observation that the exo form is the most stable.

When examining the hydrogenation of the endo dimer, there are two possible isomers that can be formed, as seen in the above table. We can see from the total energies that the hydrogenated isomer two is the most stable, with a total energy of 31.15 kcal/mol c.f. that of isomer 1 which has a total energy of 35.93 kcal/mol. Looking again at the complete energy readout we can gain some more insight as to the reason behind this enhanced stability:

Hydrogenated Isomer 1

 Stretch:          1.2324
 Bend:            18.8641
 Stretch-Bend:    -0.7625
 Torsion:         12.2469
 Non-1,4 VDW:     -1.5627
 1,4 VDW:          5.7523
 Dipole/Dipole:    0.1631
 Total Energy:     35.9337 kcal/mol

Hydrogenated Isomer 2

 Stretch:          1.0963
 Bend:            14.5074
 Stretch-Bend:    -0.5493
 Torsion:         12.4972
 Non-1,4 VDW:     -1.0507
 1,4 VDW:          4.5124
 Dipole/Dipole:    0.1407
 Total Energy:     31.1540 kcal/mol

Here we can see that the main difference in energy (overall 4.78kcal/mol)is associated with the bending energy of the isomers. This makes sense when we look at the double bond being hydrogenated. We would expect isomer 2 to be the most stable as it is the double bond which is in closest proximity to the methyl bridge which is hydrogenated, and undoubtable that which is the most strained. We can conclude therefore that the hydrogenation is a thermodynamic process, as we would expect that the most stable isomer is that which would predominate.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring

In this case, ChemBio3D will again be used to calculate the energies of the various species involved. Again the MM2 calculation will be used.However in this case the total energies of the molecules is not our main concern, instead we will focus on the geometry of the carbonyl group, and how its relative orientation with regards to the pyridine ring effects the mechanism of the reaction.

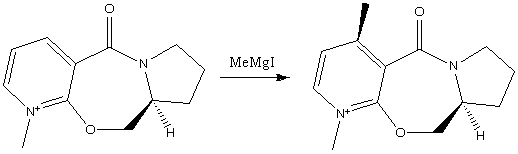
Example 1

The first example is of the optically active derivative of prolinol (the reactant in the scheme below). It reacts with MeMgI which results in the alkylation of the pyridine ring at the 4 position, and results in the absolute sterochemistry shown in the reaction scheme below.

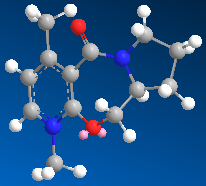
Table 2: Energies of Starting Material and Product
Reactant	Product
26.3274 kcal/mol	27.7475 kcal/mol

When running the calculation the MeMgI component was not included. If included, the calculation did not run properly, this is due to the fact that ChemBio3D cannot run calculations on molecules including a metal ion. I tried several different orientations of the carbonyl group with respect the to the pyridine ring, with the result that the orientation shown above resulted in the lowest energy. The dihedral angle between the carbonyl group and the aromatic ring is approximately 40°. Upon decreasing the dihedral angle, the overall energy of the molecule increased. Having found the lowest energy conformation of the prolinol derviative, we can start to draw conclusions from the method of attack by the methyl group. The methyl group can only attack the pyridine ring from one face. At first glance we would expect it to attack the face which is the least sterically hindered, i.e. the face which is not sterically hindered by the carbonyl group. However we see that it is the opposit which in fact occurs. This observation canbe rationalised by the the fact that as the MeMgI group approaches the pyridine ring, the delta-negative carbonyl oxygen atom and the delta postive magnesium atom experience an attractive interaction. This results in the attack of the methyl group being on the same plane as the carbonyl group.

The dissapointing thing is that it was not possible to factor in the influence of the MeMgI group into the optimisation calculation, as stated above this was due to the inability of the progrom being used to recognise the metal ion. A way to improve the result of this calculation would to be to use a program which can recognise such species, such as Gaussian.

Example 2

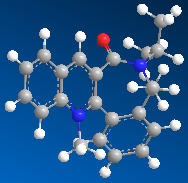
In this second example the pyridinium ring (seen in the reaction scheme below) reacts with anilline, with the result that the NHPh group adds para to the methyl group in the absolute stereochemistry seen below. The product can then act as a NHPh transfer agent to other electrophiles, such as carbonyl groups.

Table 3: Energies of Starting Material and Product
Reactant	Product
15.6605 kcal/mol	26.8422 kcal/mol

The minimum energy of the starting material was again calculated using the MM2 calculation in ChemBio3D. Again I tried different orientations of the carbonyl group with respect to the pyridine ring. The overall result mirrored that in the first example, any attempt to decrease the dihedral angle between the carbonyl group and the pyridine ring resulted in an increase in overall energy, and movement of the carbonyl group would result in the molecule being optimised to the above form, i.e. again the molecule as an absolute stereochemical configuration. However unlike the first example, there is no possible coordination between the carbonyl oxygen and a delta postive element. Therefore in this case it is sterics which goveren the method of attack. The incoming molecule is large, and so will attack on the least hindered face, which is the face not hindered by the presence of the carbonyl group. We have a sterospecific reaction, resulting in a single product.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

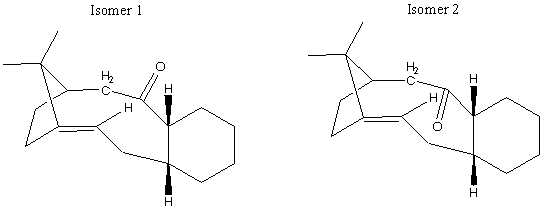
There is a key intermediate in the synthesis of Taxol, which is used as a treatment for ovarian cancers. There are two possible orientations for the carbonyl group to be in, resulting in two possible isomers:

If left, the compound will isomerise to the other isomer. This is known as atropisomerism. The overall stereochemistry (whether the carbonyl group is up or down) will depend on which isomer is the most stable, i.e that will the lowest total energy. It has also been shown that the functionalisation of the alkene is a very (unusually) slow process. Again the molecular mechanics calculation was used to identify which of the two possible isomers is the most stable.

Table 4: Key Intermediates in the Total Synthesis of Taxol
Isomer 1	Isomer 2
Ammonia-Borane	Ammonia-Borane
54.44 kcal/mol	49.97 kcal/mol

From the total energy readout we can see that the isomer with the carbonyl group pointing down (i.e. the opposite face to the bridging group) has the lowest energy.

Again it is usefull to see the whole output from the minimisation.

Isomer 1

 Stretch:         2.8136
 Bend:            16.4522
 Stretch-Bend:    0.4551
 Torsion:         21.4498
 Non-1,4 VDW:     -0.9397
 1,4 VDW:         14.0705
 Dipole/Dipole:   0.1343
 Total Energy:    54.4358 kcal/mol

Isomer 2

 Stretch:         2.6562
 Bend:            11.1589
 Stretch-Bend:    0.3829
 Torsion:         22.9597
 Non-1,4 VDW:     -1.0158
 1,4 VDW:         14.0039
 Dipole/Dipole:   -0.1732
 Total Energy:    49.9726 kcal/mol

Here we can see that the main difference in energy between the two isomers is the bending energy. Again we can see that the isomer with the carbonyl group pointing down has a significantly lower bending energy than the isomer with the carbonyl group pointing upwards. This can be rationalised by the fact that the isomer with the carbonyl group poinitng upwards suffers from more bending strain due to the fact that there is a distortion from the ideal sp² hybridised bond angle of 120°. The bond angles between the carbonyl group and the ring are 115.4° and 118.2° Compared with the down isomer which has bond angles of 119.8° and 119.5°. It is therefore logical that the up isomer is higher in energy, as the smaller bond angles means that the molecular orbitals experience a greater repuslion which raises the overall energy of the isomer.

As stated above the functionalisation of the alkene is an unusually slow process. Why should this be the case? Upon running an optimisation of the hydrogenated alkenes, it does indeed show that the alkenes have an extra stability about them, with the hydrogenated isomers having total energies of 73.48 kcal/mol (up isomer) and 72.99 kcal/mol (down isomer). The alkenes are said to be hyperstable. The extra stability of hyperstable alkenes is due the fact that upon hydrogenation the dihedral angles formed between the C-H groups are smaller than usual, resulting in a significant amount of strain.

Key literature

1. S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
2. See J. G. Vinter and H. M. R. Hoffman, J. Am. Chem. Soc., 1974, 96, 5466 (DOI:10.1021/ja00824a025 DOI:10.1021/ja00824a025 ) and 95, 3051 for another nice example of atropisomerism.
3. Another well known example is within Vancomycin: J. Am. Chem. Soc., 1999, 121, 3226. DOI: 10.1021/ja990189i
4. An interesting variation is of "atropenantioselective cycloetherification" (G.ÊIslas-Gonzalez, M.ÊBois-Choussy and J.ÊZhu, Org. Biomol. Chem., 2003, 30-32. DOI: 10.1039/b208905. See also Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI: 10.1016/j.tetasy.2004.11.004

How one Might Induce Room Temperature Hydrolysis of a Peptide

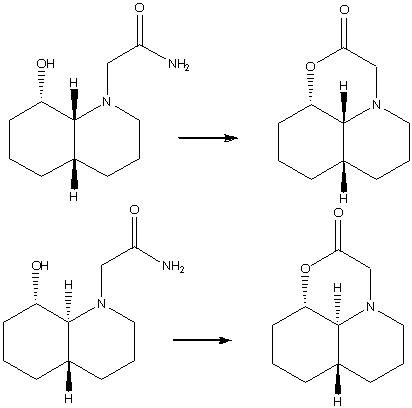
Peptides are of extreme importance in biological systems, and the half life of a peptide bond is approximately 500 years. However in biological systems there are enzymes which can hydrolise peptide bonds in less than a sceond. Organic chemistry has not yet been able to accurately replicate biological systems, however it is possible to achieve esterification of a peptide like molecule at room temperature in a time frame of approximately 20 minutes. The two isomers shown below differ only in the relative stereochemistry of the two protons where the two rings are joined, one has a cis conformation, the other trans. The interesting fact is that they react differently. The cis isomer has a half life of 21 minutes, and the trans isomer a half life of 840 minutes.

In order to model this experiment, and to determine why these peptide-like molecules hydrolyse in much less time than 500 years, again ChemBio3D was used to calculate their minimum energies. In each case the N-substituent was modified to be either axial or equatorial with the following results:

Table 5: Cis Isomer
N Substituent Axial	N Substituent Equatorial
Ammonia-Borane	Ammonia-Borane
19.87 kcal/mol	17.77 kcal/mol

Table 6: Trans Isomer
N Substituent Axial	N Substituent Equatorial
Ammonia-Borane	Ammonia-Borane
12.03 kcal/mol	10.10 kcal/mol

In the case of the cis conformation we can see that it is the isomer with the N substituent in an equatorial position which is the most stable. This is what we would have expected, as substituents prefer to be equatorial as this position avoids the 1,3-diaxial interaction experienced when the substituent is in an axial position and is therefore intrinsically more stable. With regards to the hydrolysis that takes place, the hydroxyl group must be able to attack the carbonyl with the appropriate trajectory, the Burgi-Dunitz angle. This is the angle at which nucleophiles must approach the carbonyl to ensure a maximum overlap of orbitals, and its approximately 107°. In this case it turns out that it is the conformation where the N-substituent is axial in which the best angel of approach can be achieved, and thus it will be the axial conformation that will react to the product, with the equatorial form equilibriating to the axial and reacting. An explanation for why this process is acheivable at a reasonable rate is that the groups involved in the reaction are forced into a close proximity due to that nature of the ring system, and the intramolecular nature of the reaction ensures that the appropriate groups are close together.

In the case of the trans isomer again we see that the conformer with the N substituent in an equatorial position is the most stable, for the same reasons as given above. In this case however in neither conformer is there an approximation to the Burgi Dunitz angle, so we can deduce that it will be the axial, least stable isomer which will proceed in the reaction. Again, this process is faster than peptides in the body due to the intramolecular nature of the hydrolysis.

So we can see now why the cis isomers react more quickly than the trans. The cis isomers are higher in energy, and thus less stable, and there is a closer approximation t the Burgi-Dunitz angle, and thus better orbital overalp between nucleophile and carbonyl, and thus a faster reaction. On inspection of the trans isomers, there appears to be a better arrangement in order to acheive hydrogen bonding between the hydroxyl H and the carbonyl O, which would increase the intrinsic stability of the molecule.

Key literature

1. M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416 ASAP: DOI:10.1021/jo800706y

Regioselective Addition of Dichlorocarbene

During all of the previous calculations carried out a we were using a purely mechanical model. This has advantages and disadvantages, a main disadvantage was that it could not handle any secondary orbital interactions. In this next section, such interactions will be taken into account buy using ChemBio3D to create Gaussian input files and running the calculations through Gaussian. It will be able to take into account the electrons in a molecule, and how they influence the nature of the bonds present and the spectroscopic information obtained.

Part 1

In this section ChemBio3D was used to illustrate orbital control with regards to reactivity. The program was used first to predict the optimised geometry of the following compound:

The results were as follows:

Table 7: Optimisation of Molecule

17.90 kcal/mol

 Stretch:          0.6254
 Bend:             4.7961
 Stretch-Bend:     0.0425
 Torsion:          7.6171
 Non-1,4 VDW:     -1.0693
 1,4 VDW:          5.7769
 Dipole/Dipole:    0.1119
 Total Energy:     17.9005 kcal/mol

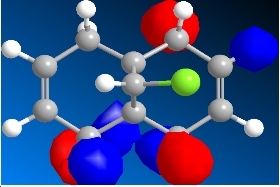
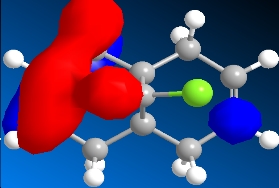
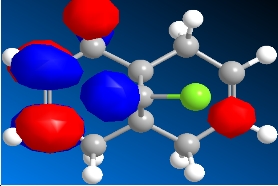
The program was then used to calculate the molecular orbitals of the molecule. This was done by running a Gaussian calculation using the HF method, and a basis set of STO-3G. The molecular surfaces property was selected and the calculation was run. The result was a visual representation of the molecular orbitals of the molecule. The isocontour was set to 0.02 to make the orbitals have a better appearance. The overall results were:

Table 8: Molecular Orbitals
HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2
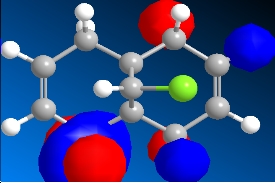
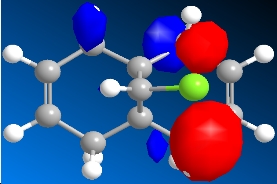
31.88 kcal/mol	34.02 kcal/mol	35.93 kcal/mol	31.15 kcal/mol	31.15 kcal/mol

We can look at the visual representation of the molecular orbitals to ascertain qualitative information about the reactivity of the species. Reactivity is governed by the frontier orbitals, i.e. The HOMO and LUMO. When an electrophile approaches the molecules, it is going to interact most strongly with the HOMO. As we can see from the visual representation of the HOMO the molecular orbital is located over the exo double bond. We can therefore predict at which double bond the dichlorocarbene will attack.

Part 2

Next we compared the molecule above with itself but where one double bond has been hydrogenated. Again both molecules were optimised using the MM2 calculation.

Table 9: Energies of Starting Material and Product
Unsaturated	Monohydrogenated
17.90 kcal/mol	22.35 kcal/mol

Next the vibrational frequencies of each compound were calculated. This was achieved by saving the optimised molecules as Gaussian input files (.gjf) and then opening them in wordpad. The files were editing so that the top lines read as follows:

1. b3lyp/6-31G(d) opt(maxcycle=30) freq

The two jobs were then submitted to the SCAN service, which was done by logging in to the SCAN website at https://scanweb.cc.imperial.ac.uk/uportal2/ and then submitting the files to Chemistry Lab 2 wall. Once the jobs were completed the formatted checkpoint files were downloaded. The files were opened in Gaussian and the vibrational results were available.

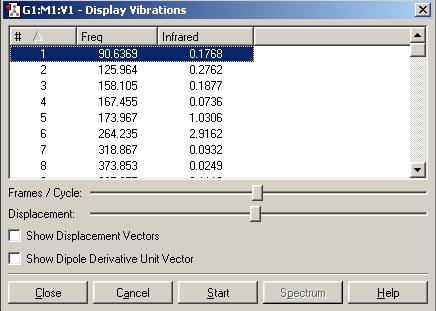
Diene

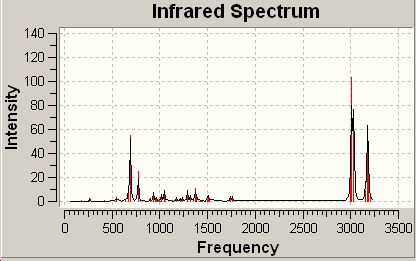
The spectrum was also provided by the calculation:

Upon using the start button the individual bends and strecthes of the molecule were show by a moving 3D molecue. This made it possible to identify what bend or stretch caused the individual frequencies.

Table 10: Diene Key Stretching Frequencies
Bond	Frequency/cm-1	IR Intensity
C-Cl	772.6	25.2
C=C	1740.8	4.1
C=C	1760.9	3.9

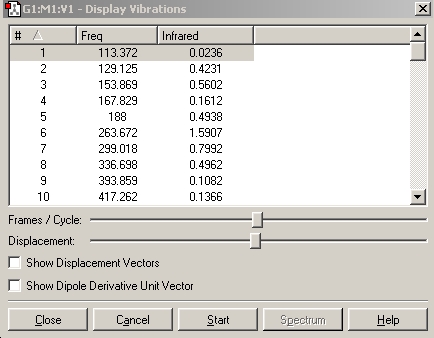
Monohydrogenated

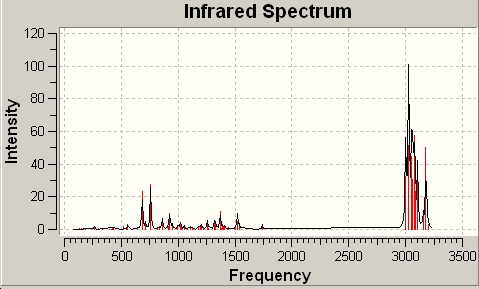
The spectrum was also provided by the calculation:

Table 11: Monohydrogenated Key Stretching Frequencies
Bond	Frequency/cm-1	IR Intensity
C-Cl	757.7	27.4
C=C	1740.6	3.2

In comparing the diene and the monohydrogenated molecules we see some differences. Obviously the monhydrogenated molecule only has one C=C stretching frequency and it is almost identical to the corresponding stretch in the diene equivalent. However there is a slight change in the frequency of the C-Cl stretch of the two molecules. This tells us that the C-Cl bond in the monohydrogenated molecule is slightly weaker.

Key literature

1. B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447

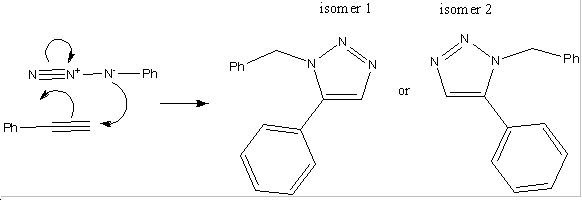
Mini Project: Assigning Regisomers in Click Chemistry

Introduction

There have been developments made in the field of 1,3-dipolar cycloadditons between alkynes and azides. It has been shown that using an Cu(I) catalyst speeds up the reaction to such an extent that reactions of that kind are now referred to as click reactions. When subsititued azides and alkynes are used in click reactions, there are two possible regioisomers which can be formed. When the copper catalyst is used, it turns out that the 1,-4 isomer predominates, however when a ruthenium catalyst is used, this favours the production of the 1-5 isomer. Below is an example of such a reaction:

Part 1

The aim of this section is to calculate the ¹³C spectra of the two isomers and to compare them with the literature values to see which shows the best comparison. This was achieved by first drawing and optimising the isomers in ChemBio3D using the MM2 calculation. The result of the initial optimisation was as follows:

Table 12: Initial Optimisation of Isomers 1 and 2
Isomer 1	Isomer 2
Ammonia-Borane	Ammonia-Borane
47.56 kcal/mol	50.87 kcal/mol

Then Gaussian input files were created, using the minimise function, and the method DFT-mp1pw91, with the basis set set to 6-31G(d,p). The file was saved and then edited in word pad so that the top line read as follows:

1. mpw1pw91/6-31(d,p) opt(maxcycle=25)

The files was resaved and then submitted to the SCAN service, which was done by logging in to the SCAN website at https://scanweb.cc.imperial.ac.uk/uportal2/ and then submitting the files to Chemistry Lab 2 wall. Once the jobs were completed the formatted checkpoint files were downloaded. Again the Gaussian input files were edited in word pad so that the top line read:

1. mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)

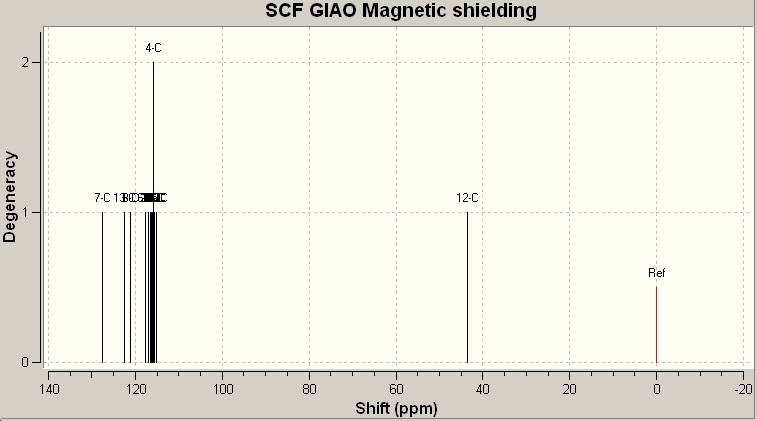
This file was then re-submitted to the SCAN service. Once this was complete the Gaussian Log file was downloaded and opened in Gaussian. Under the results tab, the NMR data was available. The carbon nucleus was selected and a reference value: TTMS HF/6-31G(d) GIAO.

Isomer 1

Now we can compare the data calculated with that given by the literature:

Table 13: 13C NMR Data/ppm
Calculated	Literature
57.06	51.81
127.52	126.93
127.89	127.22
128.21	128.22
129.36	129.08
129.38	129.64
130.08	133.26
133.61	133.3
134.97	135.66
139.94	138.26

The calculation run by the SCAN service was published on D-Space and is accessible via the follwing link:

http://hdl.handle.net/10042/to-1735

As the above table shows, there is a very strong agreement with the calcualted data, and the experimentally determined data. The next ideal step would be to compare the data obtianed for isomer one with that of isomer 2. Unfortunately there were persistent errors when trying to retrieve the files, so I have linked the Gaussian checkpoint file below:

LOG_12~2.txt