Rep:Mod:aw010288106

Computational Laboratory-Physical Laboratory

The Cope Rearrangement

The cope rearrangenment is an example of a [3,3] sigmatropic shift reaction which involves the migration of an allyl group in 1,5 hexadiene. The reaction involves the movement of 6 (4n+2) electrons and proceeds via Huckel topology with suprafacial components under thermal conditions. The reaction proceeds via a cyclic transtion state involving the combination of two allyl radicals in a boat or chair conformation with the boat conformation lying several kcal/mol higher in energy than the chair.

In this experiment the chair and boat transition structures will be located on the potential energy surface (PES) of C₆H₁₀ in order to obtain the activation eneergies and hence the preferred reaction mechanism. In order to locate the transition structures the low energy minima must first be located on the PES.

Using the gaussview programme 1,5 hexadiene was drawn, firstly with an anti linkage for the central four carbons and then with a gauche linkage for the central four carbons (results shown below).

Table showing energy of Anti and Gauche conformers of 1,5 hexadiene

	Calculation Method	Energy (Hartree)	Point Group	Dihedral Angle (°)	Appendix 1
Anti	HF/3-21G	-231.68530	C2h	180.00	anti3 Energy= -231.68907 Hartree
Gauche	HF/3-21G	-231.69167	C2	64.17	gauche2 Energy= -231.69167 Hartree

The gauche conformer was expected to be higher in energy than the anti, due to the fact that the dihedral angle in the anti conformer is equal to 180 degrees. This allows the carbon atoms to be at the furthest distance apart from each other, minimising any destabilising electronic repulsions.

Anti 2 conformation of 1,5 hexadiene

	Calculation Method	Energy (Hartree)	Point Group	Dihedral Angle (°)	Appendix 1
Anti	HF/3-21G	-231.69254	Ci	179.98	anti2 Energy= -231.69254 Hartree
Anti	B3LYP-6-31G	-234.55971	Ci	180.00	Energy= -234.611710 Hartree

When the higher level calculation method was applied the energy decreased by approximately 3 Hartree, however the geometry changed only slightly with the dihedral angle being 0.02° greater.

Infrared Spectra of B3LYP Optimised Anti Structure

Thermochemistry

Sum of electronic and zero point energies = -234.416229 Hartree

Sum of electronic and thermal energies = -234.408936 Hartree

Sum of electronic and thermal enthalpies = -234.407992 Hartree

Sum of electronic and thermal free energies = -234.447848 Hartree

Table showing thermochemistry data of anti 2 conformation

	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Anti 2	-231.69254	-231.53954	-231.53258	-234.61172	-234.46919	-234.46184
Anti 2 (Appendix 1)	-231.69254	-231.53954	-231.53257	-234.61171	-234.46920	-234.46186

Optimising the Chair and Boat Transition Structures

Chair Transition State

Method 1

In order to obtain the chair transition state a guess structure was first obtained. In order to do this a single allyl fragment (CH₂CHCH₂) was first optimised using HF/3-21G theory. Once optimised the fragment was copied and then pasted twice (using the append molecule option) into a new window in gaussview. The two resulting allyl fragments were then positioned so that the two terminal carbons were 2.2 Å apart. An opt+freq calculation was carried out with the optimisation to a TS (Berny) and calculate force constants once tabs being highlighted, also Opt=noeigen was entered in the key words box, this prevented the computer calculating more than one transition state. The results of the optimisation and frequency calculation are shown below.

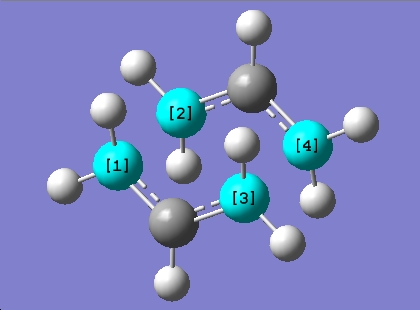
Bond lengths

C[1]-C[2] = 2.01976 Å

C[3]-C[4] = 2.02006 Å

Energy = -231.61932221 Hartree

Point Group = C_2h

Imaginary Frequency = -817.903 cm-1

IR Spectra of Chair Transition State

The imaginary frequency shows the two allyl fragemnts vibrating in a bond forming direction.

Method 2

The same guess structure was used for method 2 however the redundant coordinate editor option was utilised. Firstly the bond coordinates were frozen using this option and an optimisation to a minimum (HF/3-21G) was carried out. Once completed the optimised molecule was again re-optimised however this time the redundant coordinate editor was used to calculate the derivative of the bond, and the optimisation (HF/3-21G) carried out was to a TS (Berny) without force constants being calculated.

Bond lengths

C[1]-C[2] = 2.02067 Å

C[3]-C[4] = 2.02048 Å

Energy = -231.61932244 Hartree

Point Group = C_2h

The difference in energy between the two optimisation methods is = 1.2555 x 10^-4 kcal/mol. The bond lengths in method 2 are greater than the same bond lengths in method 1, the energy for method 2 is also lower.

Boat Transition State

The method described in the laboratory script uses a QST2 method in which the optimised reactants and products are specified. From this the calculation will attempt to find the transition state on the PES.

This method did not work this time. An error message (severe error message #2070) kept appearing everytime the calculation was run. The output file also said "try using 3 structures for transition state search". A guess transition structure was created and a QST3 calculation run to try and combat this error however another error appeared ("error termination request processed by link 9999"). Due to these errors the boat transition state was optimised using a similar method to that for method 1 above.

The optimised allyl fragement obtained in the chair TS optimisation was copied and pasted twice (using the append molecule option). The two fragments were then orientated so that a structure similar to that of the boat transition structure was formed. The distance between the terminal carbons was then set to 2.02 Å in order to encourage the optimisation to the transition state. An opt+freq calculation was carried out with the optimise to a TS (Berny) and the calculate force constants once options being selected. Opt=noeigen was entered into the key words box.

Bond lengths

C[1]-C[2] = 2.14032 Å

C[3]-C[4] = 2.14026 Å

Energy = -231.60280231 Hartree

Point Group = C_2V

Imaginary Frequency = -839.846 cm-1

The boat transition structure is a looser structure than the chair transition structure, it is higher in energy by 10.3665 kcal/mol and the bond lengths are greater by approximately 0.08 Å. The cope rearrangement would therefore prefer go via the lower energy chair transition state.

IRC Calculations

The IRC calculation follows the minimum energy path from the transition state down to a local minimum on the PES. It can be run in the forward, reverse or both directions. This enables the identification of the conformers which are linked by the transition state.

The IRC calculations here were run in the forward direction with 50 points along the IRC. The number of points specified in the calculation were not enough for a minimum to be found on the PES. To obtain the conformer located in the minimum the 50th point from the IRC calculation was optimised using a HF/3-21G calculation method. The results of the optimisations are below.

Chair

IRC Pathway (Chair)

Energy = -231.691667 Hartree (gauche2-appendix1)

Boat

IRC Pathway (Boat)

Energy = -231.692661 Hartree (gauche3-appendix1)

According to the above calculation, the boat transtion state lead to a minimum energy conformation that was lower in energy than the minimum energy chair conformation.

Summary of Energies (in Hartree)

	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*
	Electronic Energy	Sum of Electronic and Zero Point Energies	Sum of Electronic and Thermal Energies	Electronic Energy	Sum of Electronic and Zero Point Energies	Sum of Electronic and Thermal Energies
Chair TS	-231.619322	-231.466701	-231.461342	-234.556983	-234.414924	-234.409004
Boat TS	-231.602802	-231.450931	-231.445301	-234.543093	-234.402341	-234.396006

Activation Energies (in kcal/mol)

	HF/3-21G (0K) (kcal/mol)	HF/3-21G (298.15K) (kcal/mol)	B3LYP/6-21G(d) (0K) (kcal/mol)	B3LYP/6-21G(d) (298.15K) (kcal/mol)	Expt. (0K) (kcal/mol)
Chair	45.13	44.21	34.05	33.16	33.5 + 0.5
Boat	55.60	54.75	41.95	41.31	44.7 + 0.2

The activation energies from the higher level calculations are much closer to the experimental values than the lower level calculations.

The Diels Alder Cycloadditon

Cisbutadiene

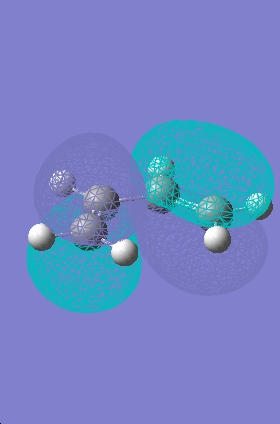
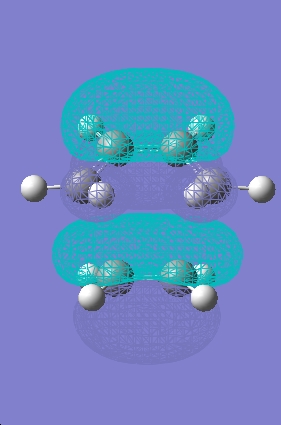
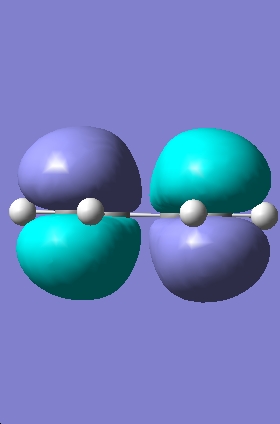
Cisbutadiene was optimised using a opt+freq semi empirircal AM1 calculation method. The HOMO and LUMO molecular orbitals were then plotted.

HOMO	LUMO
Antisymmetric	Symmetric

Transition State

The transition state was optimised by using an optimised ethylene fragment and the optimised cis butadiene fragment created above. The two fragments were positioned close enough so that the terminal carbons were 2.0 Å apart. An opt+freq optimisation to a TS (Berny) calculation was carried out with a HF/3-21G basis set and opt=noeigen as an additional keyword.

Partly formed C-C bond lengths = 2.2096 Å and 2.2099 Å

Typical sp³ and sp² bond lengths are 1.54 Å and 1.43 Å respectively. The van der Waals radius of a carbon atom is 1.70 Å. The sum of the van der Waals radi is therefore equal to 3.40 Å, since this value is greater than the C-C partly bond length there is definately a bonding interaction occcuring between the two carbons. At the transition state however, this bond length is alot greater than that of a sp³ or sp² carbon-carbon bond.

Imaginary Frequency

The bonding formation is a synchronous process as the vibration above shows the bonds forming at the same time.

Imaginary Frequency = -817.812 cm^-1

First Positive Frequency

The lowest positive frequency shows the ethylene fragment twisting from side to side, the vibration does not show any bonding forming interaction between the two fragments.

First Positive Frequency = 166.592 cm^-1

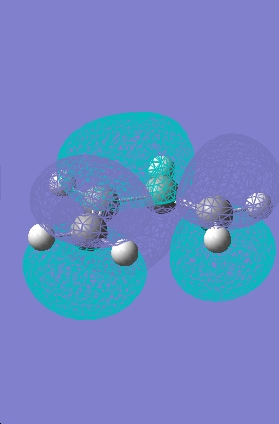
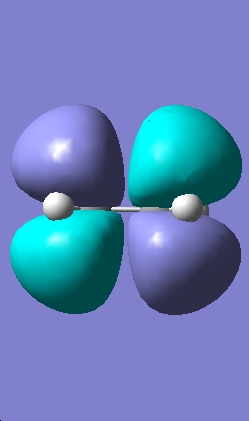
Transition State Molecular Orbitals

HOMO	LUMO
Symmetric	Symmetric

HOMO-1 (antisymmetric)

The HOMO calculated by gaussview is infact the wrong HOMO. The HOMO of the transition state is formed by the overlap of the electron rich cisbutadiene HOMO orbital with the electron poor ethylene LUMO orbital (the combination of two antisymmetric molecular orbitals), therefore the resulting MO should also be antisymmetric with respect to the reflection plane. The HOMO predicted by gaussview is symmetric with respect to the plane so is not correct. The HOMO-1 however is antisymmetric, and looks as if it has been formed by the interaction between the HOMO of cisbutadiene an the LUMO of the ethylene. The difference in energy between the HOMO and HOMO-1 is only slight (0.003eV).

Butadiene HOMO	Ethylene LUMO
antisymmetric	antisymmetric

Cyclohexa-1,3-diene Reaction with Maleic Anhydride

Endo

Endo bond lengths (Å)

• 
• 
• 

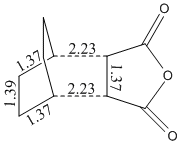
Energy = -605.61037 Hartree

Distance between C=O-CO-C=O- of the maleic anhydride and -CH=CH- of cyclohexadiene = 2.85 Å

Exo

Exo bond lengths (Å)

• 
• 
• 

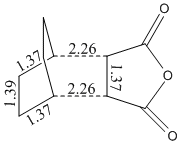
Energy = -605.60359 Hartree

Distance between C=O-CO-C=O- of the maleic anhydride and -CH2-CH2- of cyclohexadiene = 2.92 Å

Difference between two transition state conformations = 4.25 kcal/mol

The greater transition state C-C σ forming bond lengths obtained for the exo structure makes it seem like less favoured conformation. By viewing the HOMO of the two conformations it can be seen that the endo conformation has a stabilising secondary orbital overlap between a π* orbital on the cyclohexadiene and a π* orbital on the maleic anhydride, there is also a stabilising interaction between the π* orbital on the cyclohexadiene and the oxygen lone pair orbitals (shown by the two green lines on the picture). This stabilising overlap is not present in the exo conformation and it is replaced by a destabilising interaction between π* orbitals of opposite parity, increasing the energy of this form.