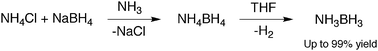Rep:Mod:aw010288

Computational Laboratory-Inorganic Component

Optimising Small Inorganic Molecules

Vibrational Analysis

A vibrational analysis calculation is effectively the calculation of the second derivative of the potential energy surface(PES) with "respect to the bond length at the equilibrium geometry". The output of this calculation can tell us where the optimised structure is (i.e. if it is in the ground state or the higher energy transition state) and also the vibrational frequencies for that particular molecule. If all of the vibrational frequencies of a molecule are positive then the optimised geometry is at a minimum however, if one of them is negative then the molecule is at a transition state. If more than one negative frequency is obtained from the calculation then the optimised molecule is stuck on a saddle point (where the gradient=0) and will need to be optimised again from a different starting point.

An optimistaion must be carried out prior to carrying out a frequency analysis calculation. In the following exercise the optimisation was carried out using a B3LYP calculation method and a LANL2MB basis set in the Gaussview programme. LANL2MB is a medium level basis set which is used because second row chlorine atoms are present in the structure which require a greater a number of mathematical functions in order to describe their electronic structure.

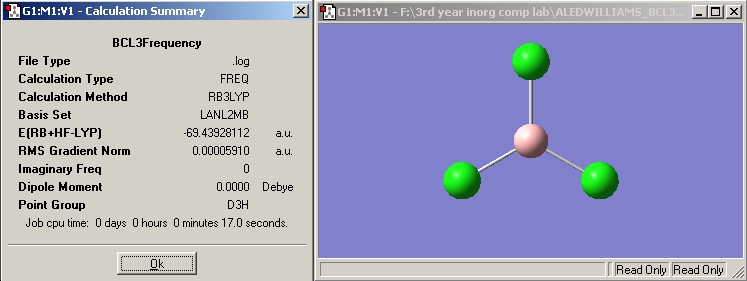
BCL₃

Optimised B-Cl distance -> 1.86592 Angstroms

Optimised Cl-B-Cl angle -> 120°

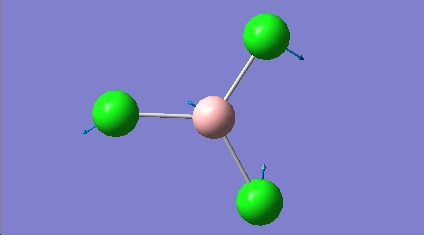
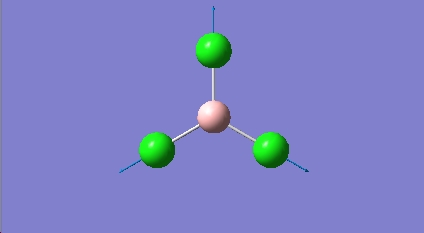
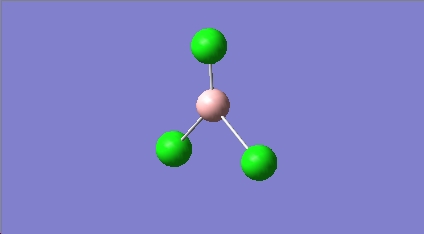
BCL₃ vibrations

No.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry D3H Point Group
1	Vibration in plane of molecule, one B-Cl bond vibrates.	214.131	3.94	Asymmetric Bend E'
2	Vibration in plane of molecule, two B-Cl bonds vibrate in a scissoring action.	214.132	3.94	Asymmetric Bend E'
3	Boron atom moves forward out of the plane of the molecule, chlorine atoms are forced slightly out of position.	376.941	43.78	Asymmetric stretch A2
4	All chlorine atoms move out and in, staying in the plane of the molecule, boron is stationary.	417.377	0	Symmetric Stretch A1'
5	Vibration in plane of molecule, boron atom moves from side to side.	939.469	258.67	Asymmetric Stretch E'
6	Boron atom moves up and down a B-Cl bond	939.470	258.67	Asymmetric Stretch E'

IR Spectrum of BCl₃

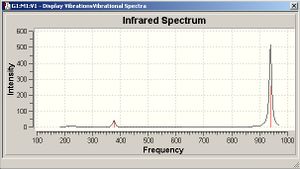
All the calculated vibrational frequencies above are positive. Therefore when optimised the energy of the molecule fell to a minimum on the potential energy surface. A non linear molecule has 3n-6 normal modes of vibration, where n is the number of atoms in the molecule. The spectra calculated for BCl₃ therefore has the correct number of vibrations. The intensities of the frequencies vary due to the size in the change of dipole moment. For the symmetric A₁' there is no change in dipole moment and so therefore A₁' is IR inactive. The difference between the two sets of degenerate E' can also be justified using the same reasoning. The absorptions at 214.1cm-1 are due to B-Cl bending vibrations, the absorptions at 939.4cm-1 are due to B-Cl stretching vibrations. Stretching vibrations involve a greater change in the dipole moment and so therefore have a much more intense absorption. Stretching a bond requires more energy than bending a bond.

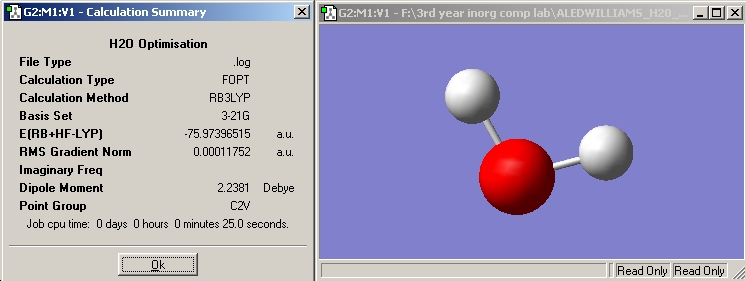
H₂O

A 3-21G basis set was used for the following optimisation. 3-21G has a lower accuracy than the LANL2MB basis set used in the previous exercise, however H₂O contains only first row elements and so does not need so many mathematical functions to describe its electronic structure. The calculation time would be expected to be less if a smaller basis set was used, in the following optimisation however the calculation time was four seconds longer than in the previous exercise. This could be due to the fact that other applications were running at the same time on the computer thus slowing the calculation down.

Optimised O-H distance -> 0.99683 Angstroms

Optimised H-B-H angle -> 103.991°

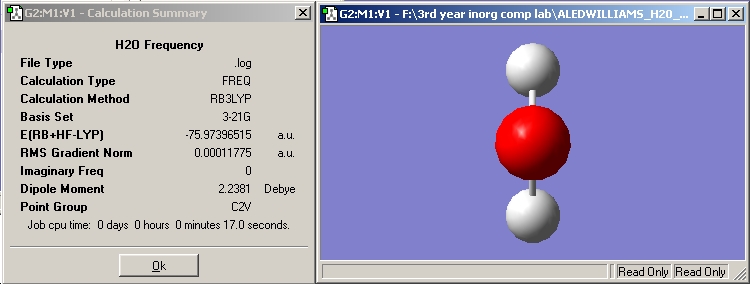
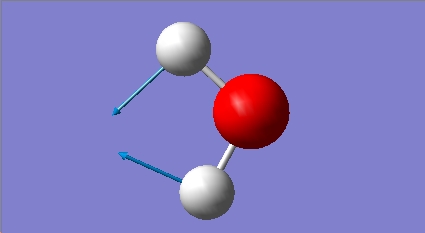
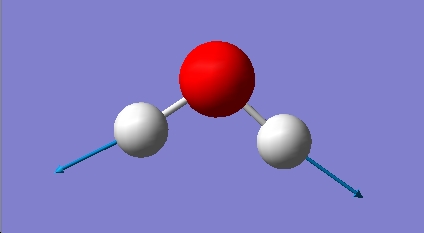
H₂O vibrations

No.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry C2V Point Group
1	The two hydrogen atoms move toward each other in a "scissoring" action, oxygen atom moves back slightly opposing motion.	1692.47	36.74	Bend A1
2	Both hydrogen atoms move in and out together, oxygen moves opposite way to hydrogen atoms.	3412.40	13.71	Symmetric stretch A1
3	One hydrogen moves out while the other moves in, oxygen atom moves toward incoming hydrogen atom.	3553.34	1.56	Asymmetric stretch B1

IR Spectrum of H₂O

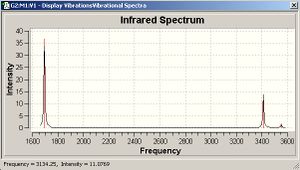
The frequency analysis shows three normal modes of vibration which agrees with the formula 3n-6. All of the vibrational frequencies are positive, therefore the optimisation has worked and the water molecule is at a minimum energy state.

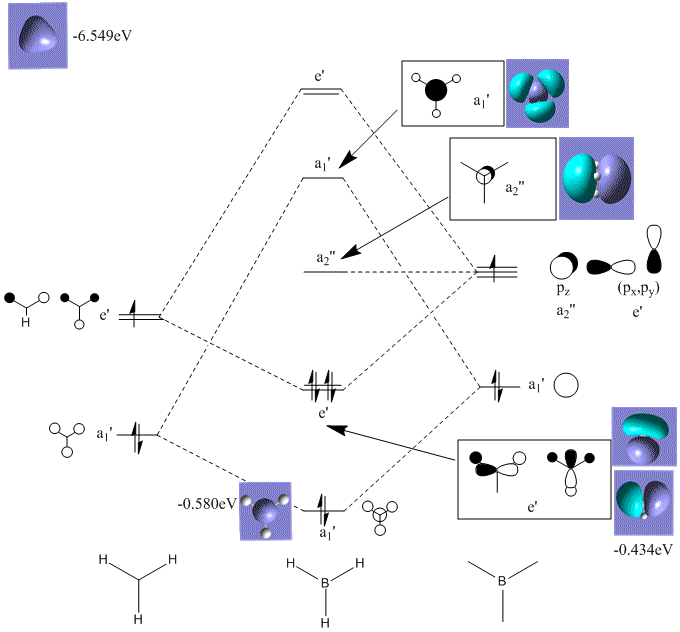
BH₃ Molecular Orbital Diagram

Gaussview calculated four occupied MO's (8 electrons). Boron and hydrogen only have six valence electrons in total so should only generate three occupied MO's. The first occupied MO calculated has an energy 6eV lower than the second occupied MO and has'nt been included in the predicted MO diagram.

Ammonia

Ammonia is a non rigid molecule which is able to tunnel between minima on its potential energy surface. "The tunneling motion is an inversion during which the molecule flips between two equivalent configurations that are mirror images of each other".

Symmetry

A 6-31G Basis set and a B3LYP calculation method will be used in this section to look at different isomers of NH₃ and the effect of symmetry on structures, energies and optimisation time.

NH3

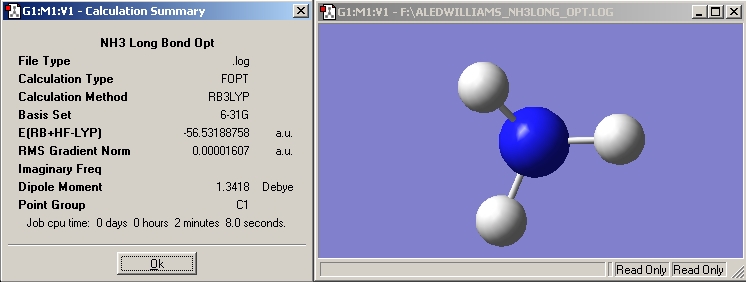
NH3 with 1 Long bond

Prior to this optimisation one N-H bond was set to 1.01 Angstroms and the ignore symmetry option was ticked. This resulted in the optimised molecule having a C1 symmetry rather than the C3V symmetry seen in the NH3 with equal bond lengths. Gaussview has a very low tolerance to symmetry, a minimal change in one of the bond lengths will affect the symmetry of the molecule. The lengthening of the bond made it lose its C3 rotational axis. The calculation time increased by 59 seconds when the bond length was increased. This was due to the ignore symmetry option being ticked. When gaussview realises it is dealing with a symmetric molecule it can avoid calculating some integrals because they have already been calculated thus reducing calculation time, in this case gaussview didn't realise it was dealing with a symmetric molecule so therefore had to carry out all of the integral calculations.

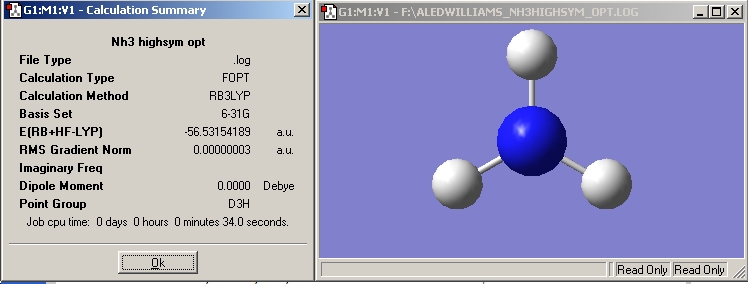
NH3 High Symmetry

In this optimisation a dummy atom has been introduced. The dummy atom forces the molecule into a geometry which would otherwise be difficult to maintain during an optimisation. The dummy atom "breaks up the problematic 180° angle into two 90° angles. The optimisation calculation took only 34 seconds (approximately half the time of the initial NH3 optimisation) due to the highly symmetrical nature of this geometry.

By viewing the step by step optimisation process it can be seen that no symmetry breaking occurs while the optimisation in process.

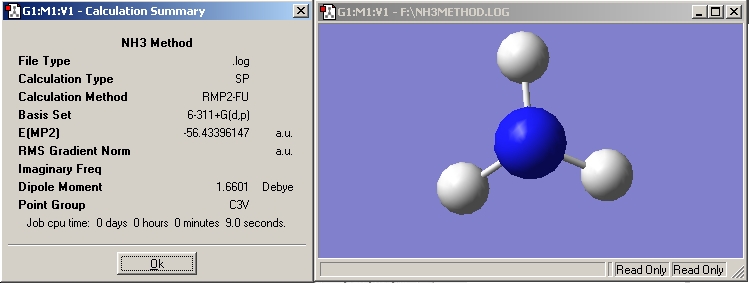
NH3

In the next two optimisations an MP2 calculation method and a 6-311+G(d,p) basis set were used.

Even though the method and basis set used here were better than previously, the calculation time was alot less. The NH3 optimisation took one minute less than with the other method.

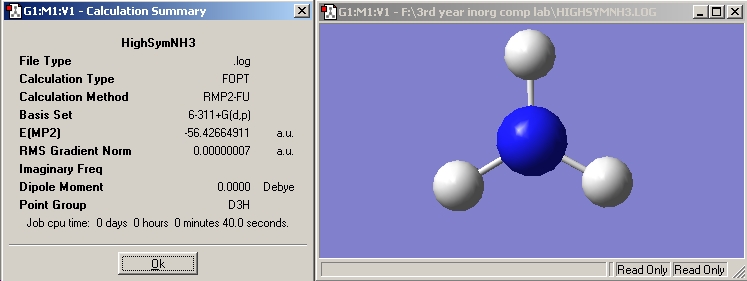
NH3 High Symmetry

The high symmetry optimisation took four seconds longer than the previous high symmetry calculation.

Summary Table

Optimisation	Calculation Method	Energy in Hartree	Point Group
NH3	B3LYP	-56.53188590	C3V
NH3 Long Bond	B3LYP	-56.53188758	C1
NH3 High Sym	B3LYP	-56.53154189	D3H
NH3	MP2	-56.43396147	C3V
NH3 High Sym	MP2	-56.42664911	D3H

The lowest energy optimisation for the B3LYP calculation method is the NH3 long bond. The energy difference between the highest energy optimisation (NH3 High Sym) and the lowest (NH3 Long Bond) is equal to 0.907609095 kJ/mol. This is an insignificant energy difference.

The energies for the MP2 calculation were higher than that of the B3LYP calculations by + 0.09892443 a.u in the C3V case and by + 0.10489278 in the D3H case. The barrier height to inversion (ΔE) can be calculated by subtracting the C3V energy from the D3H energy in kJ/mol.

Barrier height to inversion (ΔE) = 19.19860118 kJ/mol

Experimental (ΔE) = 24.3 kJ/mol

ΔE is substanstially greater for the MP2 calculations than for the B3LYP. The MP2 method provides a much better result with regard to the experimentally determined barrier height to inversion.

Vibrational Analysis

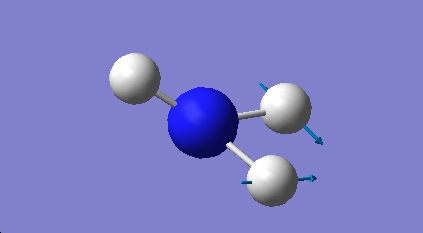
NH3-C3V SYMMETRY

No.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry C3V Point Group
1	All three hydrogens move forward together.	452.302	599.47	Bend A1
2	Two hydrogens move toward each other in a scissoring action, other hydrogen is stationary.	1680.47	41.73	Bend E
3	Two hydrogens move toward each other in a scissoring action, other hydrogen moves back and forth.	1680.47	41.72	Bend E
4	All hydrogens move in and out together, nitrogen is stationary.	3575.43	0.07	Symmetrical stretch A1
5	Two hydrogens moving away while one hydrogen moves in towards the nitrogen.	3775.76	7.09	Asymmetrical stretch E
6	One hydrogen stationary, the other two moving in and out alternatively.	3775.76	7.09	Asymmetrical stretch E

IR Spectrum of C3V NH3

The C3V frequency analysis generated six positive vibrations. Therefore the optimisation has succesfully moved the molecule to a minimum on the potential energy surface. This is the ground state conformation of ammonia.

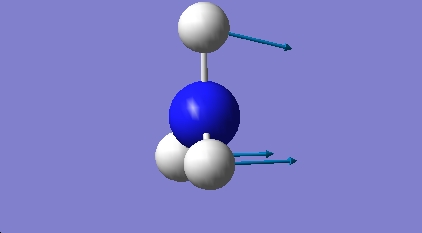
NH3-D3H SYMMETRY

No.	Form of the vibration	Frequency (cm-1)	Intensity	Symmetry D3H Point Group
1	All hydrogens move out of molecular plane.	-318.051	849.113	-
2	Two hydrogens move toward each other in a scisooring action. Nitrogen and other hydrogen are stationary.	1640.59	55.9828	Bend E'
3	Two hydrogens move toward each other in scissoring action, one hydrogen moves back and forth.	1640.59	55.9805	Bend E'
4	All hydrogens move in and out together in a symmetrical manner, nitrogen is stationary.	3635.71	0	Symmetrical stretch A1
5	One hydrogen stationary, other two hydrogen move in and out alternatively.	3854.27	19.5951	Asymmetrical stretch E'
6	Two hydrogens move out, one hydrogen moves in.	3854.27	19.5963	Asymmetrical stretch E'

IR Spectrum of D3H NH3

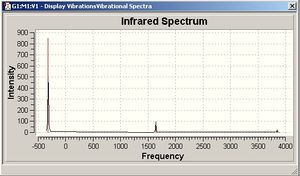
The D3H frequency analysis generates six vibrations. One of these (-318.051cm-1) has a negative value and indicates a transition state geometry.

Transition Metal Complex

Mo(CO)₄L₂ where L = P(CH₃)₃

The aim of this exercise was to prepare and then examine the vibrational spectra of the cis and trans isomers of M(CO)₄.

The molecules were first constructed in chembio 3D and then imported into gaussview as a .gjf. In order to get a good optimisation two calculations were carried out on an overnight SCAN service. The first calculation used a B3LYP calculation method with a LANL2MB basis set. Once this had completed the optimised file was downloaded then resubmitted for a further optimisation using the better LANL2-DZ basis set but keeping the same calculation method. The optimised files were then again resubmitted for a frequency analysis. The optimisations and frequencies are shown below.

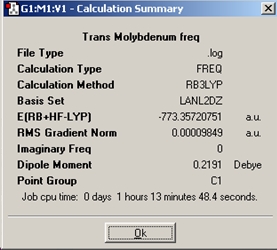
Trans

The optimisation summary describes the molecule as having C1 symmetry, however on closer inspection a C2 rotational axis is present in the molecule. The literature for a similar molecule to this describes it as having D₄H symmetry.

Table showing various bond lengths and bond angles of optimised molecule and similar literature compound

	Optimised Molecule	Lit. Value
Mo-P	2.0286 Å	2.4256 Å
Mo-C	2.02856 Å 2.02852 Å	2.041 Å 2.037 Å
P-Mo-P	180°	176.69°
Mo-P-R	117.094° 117.060° 115.683°	121.020° 120.520° 111.560°

IR Spectra of Trans Compound

	Optimised Molecule	Lit. Value
Absorption (cm-1)	1839.44	1891.83

The infrared spectra of the trans compound shows one distinct peak at 1839.44cm-1. This is expected as the trans isomer contains four equivalent CO stretching modes with only one of them being IR active. This absorption is due to the asymmetric stretching of two trans carbonyl groups.

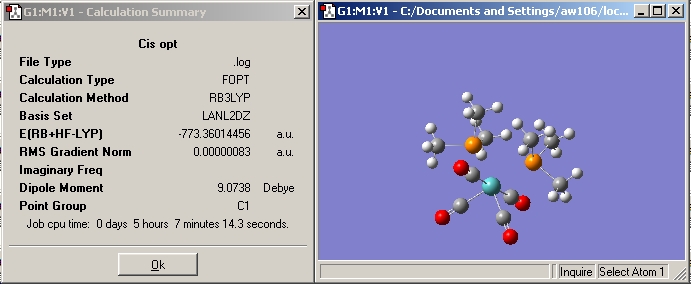
Cis

In the cis summary file (shown above) the symmetry is described as being C1. A C2 rotational axis is however present in the molecule. In literature a very similar molecule has been given a point group symmetry of C2V, which would explain the frequency analysis below.

Table showing various bond lengths and bond angles of optimised molecule and similar literature compound

	Optimised molecule	Lit.value
Mo-P	2.64775 Å 2.64813 Å	2.525 Å 2.533 Å
Mo-C	1.98191 Å 1.98217 Å 2.03266 Å	1.981 1.983 2.034
P-Mo-P	92.9°	94.78°
Mo-P-R	113.896° 118.260° 118.541°	112.9° 114.9° 121.1°

IR Spectra of the cis compound

	Optimised Molecule	Lit.Value
Absorption (cm-1)	1849.72 1850.91 1870.39 1960.71	1882 1903 1917 2022

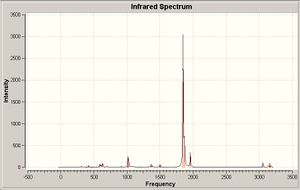
Only two peaks are clearly seen in the infrared spectra of the cis compound. There are however four absorptions shown in the output file with significant absorption intensities. The cis compound unlike the trans is expected to produce four different stretching modes ("One medium intensity band at the highest frequency and three closely spaced intense bands at lower frequencies") produced by four asymmetric stretches of the carbonyl groups. Assuming the cis isomer is of C2V symmetry the symmetry of each stretch can be assigned.

1960.71 = A₁

1870.39 = A₁

1850.91 = B₁

1849.72 = B₂

The cis isomer is the lower in energy and hence the more stable isomer of the two. The energy difference between them is 7.43909 kJ/mol.

Mini Project-Fuels of the Future-NH₃BH₃

Ammonia borane (NH3BH3) is a white, stable, solid material at room temperature. Its high hydrogen content and stability make it a good candidate for hydrogen fuel cells. NH3BH3 can be made by passing diborane gas into liquid ammonia, this method however produces product in low yield. A new method for producing the compound was discovered earlier this year and it involves a metathesis reaction in which NH4BH4 is formed in situ by reaction of NH4X and MBH4 (M=Na,Li; X=Cl,F) in liquid ammonia. The NH4BH4 is then decomposed in an organic ether to yield NH3BH3 in a much higher yield than previously seen.

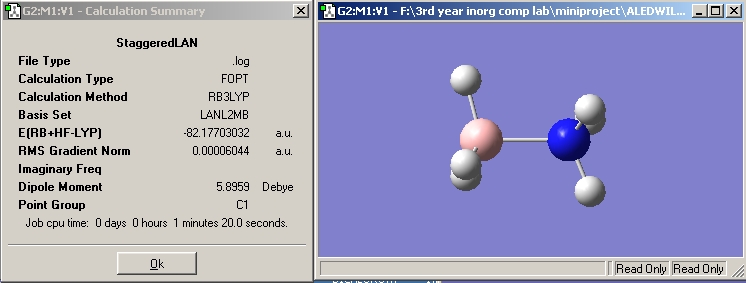
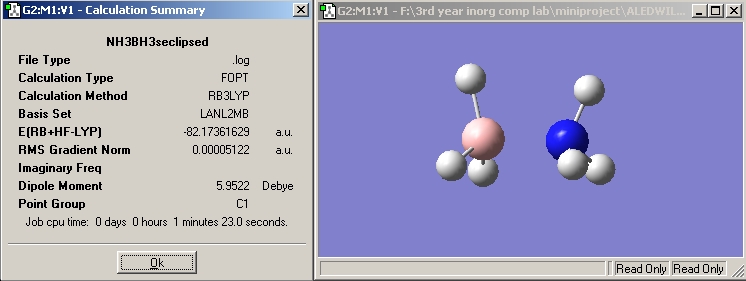
In the following calculation method (B3LYP with a LANL2MB basis set) the staggered and eclipsed forms of ammonia borane were optimised using the gaussview programme to see which form is the most stable, and hence which conformer NH3BH3 exists in.

The staggered conformation is preferred by 8.9635357 kJ/mol, this is because the distance between adajacent hydrogen atoms is greater by 0.19626 Å, reducing electronic repulsions.

Dative bond in NH3BH3

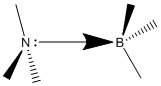
The N-B bond in ammonia borane is an example of a dative bond. The nitrogen lone pair (HOMO) interacts with the lewis acidic boron molecule, occupying its vacant p orbital (LUMO). The length of this bond is 1.65602 Å. This value is greater than the C-C sp³ σ bonded atoms in the ethane molecule (1.55177 Å). The N-B bond is therefore a weaker interaction. Due to this weaker/longer bond the hydrogen atoms on the boron and nitrogen are further apart than they are in ethane. Therefore when the hydrogens are eclipsed the repulsion between opposite hydrogens is reduced, lowering the energy difference between conformers.

Distance between opposite hydrogens in eclipsed conformation

	NH3BH3	Ethane
H-------H	2.38036 Å	2.35641 Å
Difference in energy between staggered and eclipsed conformers.	8.9635 kJ/mol	10.9740 kJ/mol

Ammonia borane and ethane are isoelectronic with one another. At room temperature ethane is a colourless gas whereas ammonia borane is a solid molecular crystal. This can be explained by a network of dihydrogen bonds between adjacent molecules . The hydrogen bonds are formed due to the nature of the polarity of the N-B bond. Nitrogen is more electronegative (3.4) than boron (2.4), the nitrogen hydrogen atoms are protic in character, the boron hydrogen atoms are hydridic in character, creating a N-H----H-B network of hydrogen bonds which increase the melting point of the structure.