The Cope Rearrangement

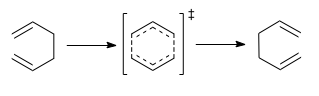
The Cope Rearrangement involves a concerted [3,3]-Sigmatropic alkyl shift in a 1,5-diene system. The reaction proceeds thermally, via a Huckel topography, with Suprafacial sterochemistry. We are going to show this statement to be true, by using computational methods to study this reaction.

In the most simple case of a Cope reaction, 1,5-hexadiene rearranges. The product is the same as the reactant, but with the order of the atoms changed. We shall initially investigate this reaction, first looking at the geometry of 1,5-hexadiene to determine the most stable conformer, and why, and then explore various methods of optimising the transition state of the reaction.

The Cope Rearrangement of 1,5-Hexadiene

Optimising the Geometry of 1,5-Hexadiene

Initially, we shall optimise a molecule of 1,5-Hexadiene, exploring the geometries of different conformations, asking why certain conformations are lower in energy than others.

Using the Gaussview 3.09 GUI, a molecule of 1,5-hexadiene was created, with anti-stereochemistry across the central C-C bond (the Dihedral angle was set to 180^o). This was optimised using the HF/3-21G Level of theory. The calculation optimised the molecule to a C₂-symmetric geometry, with energy -231.69260 Eh = -145389.42 kcalmol^-1. This corresponds to the Anti-1 geometry listed in appendix 1.^[1] According to appendix 1, we have found the lowest energy conformation of anti-1,5-hexadiene.

Next, a molecule of gauche-1,5-hexadiene was created (the Dihedral angle across the central C-C set to 60^o). An optimisation was again run, using the same level of theory. The optimised geometry was again C₂-symmetric, with an energy of -231.69167 Eh = -145388.84 kcal mol^-1. The energy of this gauche conformation, corresponding to Gauche-2 in appendix 1^[1], was 0.59Kcalmol^-1 higher in energy than the Anti-1 conformation we first optimised to. Why was this conformation higher in energy than the anti conformation?^[2]

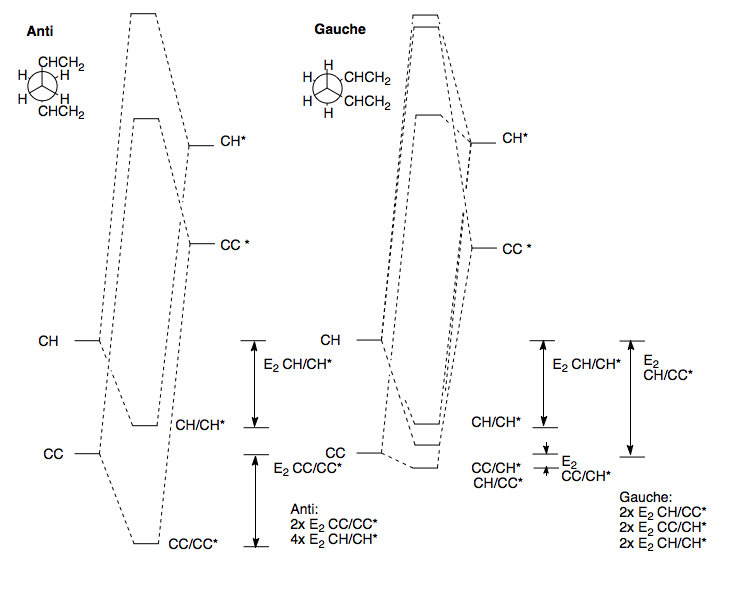
We need to consider the favorable secondary orbital overlap between σ/σ* orbitals in anti-relationships. Both conformations are staggered, so every bond has an anti-relationship to another bond. In the anti-conformer, if we look at those relationships, we see we have 2σ_CC/σ_CC* and 4σ_CH/σ_CH*. In the gauche-conformer, we now have 2σ_CC/σ_CH*, 2σ_CH/σ_CC* and 2σ_CH/σ_CH*. We can draw up a qualitative energy level diagram showing E₂ stabilising secondary interaction between orbitals, to explain the preference for the anti-conformation.

First, we define the position of the CC and CH σ and σ* orbitals. We know that the σ_CC is lower in energy than the σ_CH, because the two C sp³ orbitals are equal in energy, so are split more than a CH pair, because the C sp³ and H s orbital are apart in energy. The same is true for the σ* orbitals. In the anti conformation, the secondary overlap between σ_CC/σ_CC* produces a stabilisation. Likewise for the σ_CH/σ_CH* overlap. We would expect the σ_CC/σ_CC* overlap to be slightly more stabilising than the σ_CH/σ_CH* stabilisation, because the σ/σ* gap would be less, because the C FO's atoms are more evenly matched in energy. In the gauche-conformer, we also have the σ_CH/σ_CH* overlap, but now no σ_CC/σ_CC* overlap. Instead we have σ_CC/σ_CH* overlap, which is very little stabilising, because the orbitals are far apart in energy, and a σ_CH/σ_CC* overlap, which is more stabilising than the σ^CH/σ_CH* overlap, because the orbitals are closer in energy. Adding up the total number of interactions, we would expect the anti-conformer to be lower in energy, because, overall, the overlap of HOMO σ/σ* pairs will be more stabilising that the overlap of HOMO and HETRO σ/σ* pairs. This agrees with the resulting energy from calculation.

However, we also need to consider interactions between non-bonded pairs of atoms - The van der Waals interaction. This is the anisotropic interaction between two non-bonded atoms separated by a distance r. If r is very small, then the interaction is repulsive, due to n/n and e/e repulsions. If r is large, then the atoms are too far to be influenced. If r however is ideal, then the stabilising n/e Coulombic interaction is balanced by n/n and e/e and overall we have a lower energy. This is the sum of the two van der Waals radii of the atoms involved. Even if the distance is slightly larger than this distance though, the interaction is still attractive, since this is over a large range. If we inspect the anti and gauche conformers, we see that the Gauche conformer sets up more of these interactions by folding in on itself. However, as we have seen, overall, the energy of the anti conformer is lower, but not by a great deal.

Based on what we have just said, we could imagine a lower energy gauche-conformer. If in the current gauche conformer, one CH₂CH group twisted 180^o, then one H atoms is moved within the molecule somewhat, and into the attractive region of more carbon and hydrogen atoms. Also, this twist means the two 'halves' of the molecule are not not directly over each other in space - before, they were, but they were far away, so steric bumping is unlikely, but may make a slight repulsive contribution. This has however now been removed. We took the gauche-conformation, twisted a CH₂CH group by 180^o, and then optimised to HF/3-21G level of theory, and the resulting energy was -231.69266 Eh = -145389.46 kcalmol^-1. The resulting geometry was C₁-symmetric, corresponding to Gauche-3 in Appendix 1^[1]. This is 0.62 kcalmol^-1 more stable than the other Gauche conformer, by virtue of extra attractive van der Waals interactions. Also, this is 0.036 kcalmol^-1 more stable than the anti conformer. This is surprising, showing that the van der Waals interactions do make a significant contribution to the energy of the molecule, and in this case, overall, the energy is lower, by a small amount. However, in the Gauche conformers, we saw we have many van der Waals interactions, whereas in the anti conformer, we had few, so we can say overall, that on the anti-conformer, the σ/σ* is greater than in the gauche-conformers.

We should also be able to imagine another low-energy conformation of the anti-geometry. In Anti-1, the CH₂CH groups are both twisted the same way with respect to the central anti-linkage, resulting in C₂ symmetry. Above, we twisted one group and found a lower energy gauche conformer. Let's do the same now. Twisting one CH₂CH group and optimising to HF/3-21G resulted in a C_i-symmetric geometry with energy -231.692535 Eh = -145389.38 kcalmol^-1, corresponding to Anti-2 in appendix 1^[1]. This is 0.042 kcalmol^-1 higher in energy than the Anti-1 conformer. In this case, twisting of the group did not result in a lower energy conformer.

1,5-Hexadiene Conformers /HF 3-21G

Conformer

Anti-1

Anti-2

Gauche-2

Gauche-3

Geometry

1,5-Hexadiene Anti-1

1,5-Hexadiene Anti-2

1,5-Hexadiene Gauche-2

1,5-Hexadiene Gauche-3

Energy /Eh

-231.69260

-231.69254

-231.69167

-231.69266

Relative Energy /kcalmol^-1

0.036

0.078

0.62

0.0

Let us make a comparison between different levels of theory. Above, we used HF/3-21G. Now, we are going to take our low-energy conformer, listed in the table above and re-optimise, using DFT/B3LYP/6-31G*. We shall also carry out a frequency analysis for these geometries, to verify that we have indeed reached a minimum.

Comparison between levels of theory in the optimisation of 1,5-Hexadiene
Conformer	HF 3-21G Energy /Eh	*DFT B3LYP 6-31G Energy /Eh**	Difference /Eh	HF 3-21G Relative Energy /kcalmol^-1	*DFT B3LYP 6-31G Relative Energy /kcalmol^-1**	Imaginary modes /cm^-1
Anti-1 (C₂)	-231.69260	-234.61180	2.91920	0.036	0.0	-8.41 -3.82
Anti-2 (C_i)	-231.69254	-234.61172	2.91902	0.078	0.052	-6.20
Gauche-2 (C₂)	-231.69167	-234.61069	2.91867	0.62	0.70	-13.97 -13.36 -11.10
Gauche-3 (C₁)	-231.69266	-234.61133	2.91918	0.0	0.30	-4.40

Between the two sets of theory, we see that the higher level DFT method has calculated a different relative energy order of our conformers. The two levels of theory do however give the same order of stabilities between the pairs of anti- and gauche- conformers, so this suggests that the DFT calculated a greater σ/σ* stabilising interaction, or a weak vdW stabilising interaction. Hence, the gauche are calculated to be less stable than the anti conformers under DFT/B3LYP/6-31G*.

There is however, a slightly worrying result when we look at the imaginary frequencies. These should all be zero, if we have indeed optimised to a minimum. I think perhaps using this mid level basis set, that the geometry hasn't quite reached the minimum. Because the energy differences are very small between conformers, a slight difference in geometry could lead us to an incorrect order of relative energies. Hence, the optimisation was rerun again, from the DFT result, this time specifying very tight convergence criteria, and int=ultrafine This is computationally expensive, but I think it is necessary to establish which is the lowest energy conformer. The results:

*DFT B3LYP 6-31G Very tight optimisation 1,5-Hexadiene Conformers**
Energy /Eh	Relative Energy /kcalmol^-1	Imaginary modes /cm^-1
Anti-1 (C₂)	-234.61179	0.0	-6.6 -3.2
Anti-2 (C_i)	-234.61171	0.051	-5.6 -1.9
Gauche-2 (C₂)	-234.61070	0.68	-5.8 -5.4 -4.2
Gauche-3 (C₁)	-234.61133	0.29	-0.0004

This very tight convergence reduced the magnitude of all of the imaginary modes, showing the geometry is moving toward the bottom of the potential well. The key result here is that the energy changed only by ~0.01 kcalmol^-1, and the order of conformers did not change. If we consider the potential surface for this molecule, we expect wells for the conformers we have found. For the two pairs of anti and gauche conformers, the geometry difference is not a great deal, so the wells are close, and probably not very steep barrier between them. Hence, this may also explain why we get small imaginary frequencies – we are not at a transition structure, but in a shallow well, not quite at the bottom. Because this result agrees with that for the quicker calculation, we shall use the DFT B3LYP 6-31G* theory for further analysis.

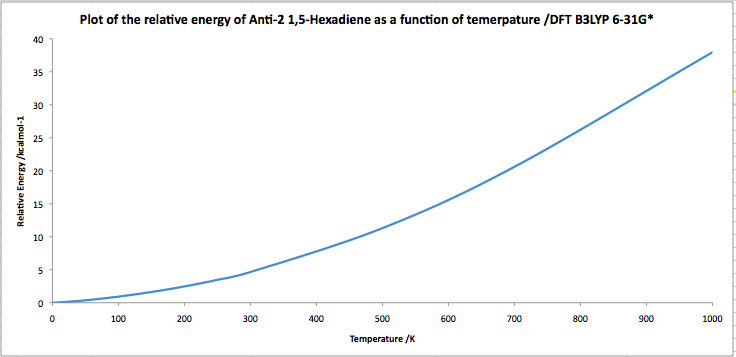
The energies reported are for the conformations at 0K. Carrying out a frequency analysis allows us to make a correction to other temperatures, specified using a readisotopes keyword. Using the Anti-2 conformer, we are going to investigate the effect of increasing temperature on the energy of the system, taking into account the thermal correction, by calculating the thermal correction at a range of temperatures, by specifying a frequency calculation to the DFT B3LYP 6-31G* level, with the readisotopes tag, on a DFT B3LYP 6-31Gd optimised geometry, and then plotting the resulting Sum of Electronic, ZPE and thermal energies.

We initially see that at low temperatures, the energy is increasing, at an increasing rate with increasing temperature, until a point where the increase in energy of the system is linear with temperature. At T=0K, all the molecules are in their vibrational ground state. As T is raised, but kept low, the first few vibrationally excited states begin to be populated. Increasing the thermal energy further will populate more states until it gets to a point where all the vibrational states are filled. In this regime, we see an increasing rate of change of energy with temperature. At this point, the discrete properties of the molecules can be treated classically, i.e the vibrational temperature. After this temperature is surpassed, the molecule behaves classically, and its increase in energy is linear with temperature.

Locating the Transition State Structures

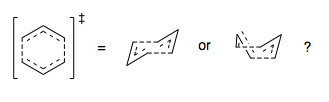
We are going to use a variety of methods to explore the transition state geometries of this rearrangement. Initially, we shall form a guess, consisting of two allyl- fragments separated in space, with the correct symmetry to hopefully optimise to the transition structure. We shall use the Berny TS method to optimise, and also the 'Frozen' Coordinate, two-stage optimisation method. Then, we shall use the QST2 method, now, not forming a transition state guess, but interpolating between the starting material and product.

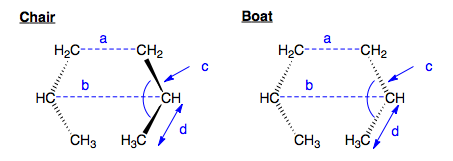
If we consider two allyl fragments separated in space, we can form two potential transition state structures, corresponding to chair and boat cyclohexyl-like geometries. We shall explore both reaction pathways, via chair and boat TS structures, to determine which is the lower energy, and hence more favorable process.

Berny Optimisation

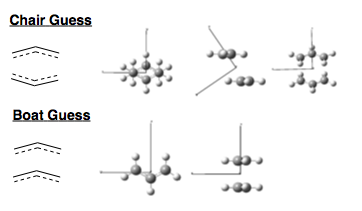
Using Gaussview 3.09 GUI, an allyl, C₃H₅, fragment was created. This was optimised using HF 3-21G theory, and the resulting geometry was then used to build our transition state guesses. Two of these fragments were placed face on, one overlapping directly, to give a C₂v-symmetric geometry - Boat, and once with one fragment rotated, with a terminal C overlapping with terminal H on the other fragment, to give a C₂h-symmetric geometry - Chair. The two allyl fragments were set 2.2Å apart in both starting guesses.

These structures were then optimised to a Transition State, using the Berny method and HF/3-21G theory, calculating the force constants once. The resulting geometries are shown below. In both structures, the central C atom of the allyl fragments pucker away from the other fragment slightly. In the chair C₂h structure, the terminal C atoms are separated by 2.02Å. In the C₂v boat, they are separated by 2.14Å.

HF 3-21G TS(Berny) Opt results

Chair-C₂h

Boat-C₂v

Cope Chair TS Benry Optimisation result

Cope Boat TS Benry Optimisation result

Note that although Jmol draws these as propene fragments, the two C-C bond lengths in each fragment are equal and they are in reality allyl- like. How do we know these are transition states? We look for one imaginary mode, corresponding to the displacement either side of the transition state. In the Chair-C₂h TS, we find exactly that, an imaginary frequency with magnitude 817cm^-1. Likewise, in the Boat-C₂v TS, at magnitude 840cm^-1. Animating these imaginary modes, we see each allyl fragment bend back and forth from each other. This is the Cope rearrangement.

HF 3-21G TS(Berny) Opt Imaginary modes

Chair-C₂h

Boat-C₂v

Cope Chair TS Imaginary Mode

Cope Boat TS Imaginary Mode

-817cm^-1

-840cm^-1

Frozen Coordinate Optimisation

The transition state structure guesses were taken and using the redundant coordinate tool in Gaussview, the terminal C atoms of the two fragments were frozen, at a set distance of 2.2Å apart. What this does is fix the position of these atoms when we optimise the structure. We carried out a HF/3-21G Opt=Modredundant calculation. In the resulting geometry, the central C atoms had puckered out slightly, as they did above, but as we said, the terminal atoms stayed fixed. Then we took this resulting geometry and optimised again, using the same theory, this time without the condition of being fixed, but to differentiate along the forming and breaking bonds to find the transition state. The value in this method is that we do not have to calculate force constants, which for large jobs will be less computationally expensive.

How do these compare to the Berny Results? If we measure the following geometric parameters, in both the chair and boat structures for both optimisation methods, we find them to be be identical to 0.01Å and 0.1^o. Hence, we can say that for this simple system, both methods of optimising a transition state from a guess are equally valid.

Comparing Optimised TS structures for two different methods

Parameter	HF 3-21G Berny TS Optimisation		HF 3-21G Frozen Coordinate TS Optimisation
Parameter	Chair	Boat	Chair	Boat
a	2.02	2.14	2.02	2.14
b	2.88	2.78	2.88	2.78
c	120.5	121.7	120.5	121.7
d	1.39	1.38	1.39	1.38

QST2 and QST3

As well as being able to set up a guess geometry of a transition state,and optimise to it using the two methods above, we can also carry out a QST2 calculation, whereby we interpolate between starting material and product, to locate the transition state along that path. This is what we shall attempt to do here, for the boat transition state

We shall take out Anti-2 C_i 1,5-Hexadiene Conformer. As we saw, this is not the lowest energy conformer, but is only ca. 0.5 kcalmol^-1 higher in energy, so is very thermally accessible. We are going to take this conformer because, as we shall see, it has symmetry about a point, and when we set the dihedral, to come, about a plane, so the interpolation will be easier, and hence less computationally expensive and more likley to work

A necessary condition for QST2 is that the order of atoms in the reactant input metches that in the product input. Because the reactant and product are the same molecule, but a different order of atoms, our first task is to create a molgroup, with two frames of the same stutcure, then renumber the second frame accordingly, so that when the molecule rearranges via a [3,3] shift, the order is the same. Once this was done, a HF 3-21G QST2 calculation was carried out. This job however, failed and produced an erronious geometry. This is because the simple interpolation moved atoms about, but looking at the geometries, we can easily see that to be able to get to the transition sate, the C_i anti structure clearly needs first to rotate about the central C-C. We then took the starting geometries from the failed QST2 job, and set the central C₄ dihedral to 0^o. Then the two halves of the molecule were brought closer together by setting internal bond angles to both be 100^o. This structure has symmetry about a plane passing across the centre of the molecule, hence, when we interpolate between the two, we should find the boat transition state, since it also has that plane-symmetry. The calculation was rerun from these starting geometries.

Boat QST2 TS Optimisation start and end points: Failed job		Boat QST2 TS Optimisation start and end points: Rotated Dihedral
Start Point	End Point	Start Point	End Point

The result is indeed that expected - the boat transition state. Again, when we compare the resulting structural parameters to those listed above, we find them to be the same.

For more complex jobs, it is possible to specify a guess structure for the transition state - for example, here we could place in the guesses from above. This would then be a QST3 calculation. However, here it will be unnecessary, since some though as to the starting geometry emabld us to quickly find the transition state.

Following the reaction pathway: IRC

We have found chair and boat transition structures for the Cope rearrangement of 1,5-Hexadiene. Now we need to determine which starting conformation is necessary to reach those transition states. To do this, we use the Intrisic Reaction Coordinate method. Here, we start at the geometry of our chosen transiton state to investigate, and we choose to follow the reaction path as the energy decreases down to a minimum geometry - we are following the reaction coordinate in an energy profile plot. In ths case of the Cope rearragment, the profile will be symmetrical about the transntion state (same molecule and conformation) but usually products have lower energy than reactants, hence, we usually follow the path in both directions but here we only have to go in one direction.

From the optimised geometry of the transition state, taken from the results of the Berny Optimisation (althogh as we saw the other methods gave the same structure), an IRC calculation was carried out, to follow the forward direction, with a maximum number of points set to 200, and specifying that the force constants be calculated at every step. Because we set the calculation to see if we have reached a minimum at every step, we don't risk not finding the true minimum. It doesn't take 200 steps to run, the aim of this was to allow the calculation to find the minimum without risking it not reaching it.

If we observe the strctures of the final IRC geometry, we can judge which conformer the reaction proceeds from. From the Chair-TS IRC results, we find that the Gauche-2 confomation gives the necessary orientation for this rearrangement. The boat form however converges to a staggered form, which as we know is itself a transition state between lower energy gauche and/or anti conformations. This first seems to sugest the IRC failed, but if we consider that the caluclation finds the nearest minimum in the give direction, then this condition is fulfilled by a transition state - just the wrong type. Then, to find the nearest stable conformer, we can run another IRC on the resulting staggered geometry. Doing this, we find the calculation converges to the Gauche-3 conformer, by rotation by 60^o of the central C-C bond.

These two starting conformations are, as we saw, not the lowest energy conformers. However, all the conformers, and the transition states between them were thermally accessible, i.e this system did not exhibit atropisomerism, taking an ensemble average of the system we would find a certain proportion of the molecules to be in each state, with smaller proportions for higher energy conformations.

We also see, by plotting together the energy difference between reactant and product for the two pathways, we find that the boat transition state is higher in energy than the chair transition state on the pathway between their respective conformations to allow reaction.

To be able to report a calculated activation energy for the reaction, we first need to reoptimise our transition structures to DFT B3LYP 6/31G* theory, and compare their energies to that of the Anti-1 conformer, since by convention the activation energy is reported relative to the lowest energy conformer. The activation energy between chair TS and Anti-1 Conformer is cauclated to be 34.4 kcalmol^-1. The experimentally determined value is 33.5±0.5kcalmol^-1. The activation energy between boat TS and Anti-1 Conformer is calculated to be 43.1 kcalmol^-1. The experimentally determined value is 44.7±0.2 kcalmol^-1. These are at 0K. The values are very close to those from experiment, showing the power of these computational methods.

↑ ^1.0 ^1.1 ^1.2 ^1.3 Mod:phys3#Appendix_1
↑ http://www.ch.ic.ac.uk/local/organic/conf/

General references made throughout to:

M.Bearpark, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3, 2008

J.B.Foresman and A.Frisch, Exploring Chemistry with Electronic Structure Methods, 1996

Index

The Cope Rearrangement

The Diels Alder Cycloaddition

The Pathway to Adamantane...

[one-1] 1.0 ^1.1 ^1.2 ^1.3 Mod:phys3#Appendix_1

[rzepa-2] ttp://www.ch.ic.ac.uk/local/organic/conf/

[1]

[2]