Rep:Mod:asp216 Y2
EX3 section
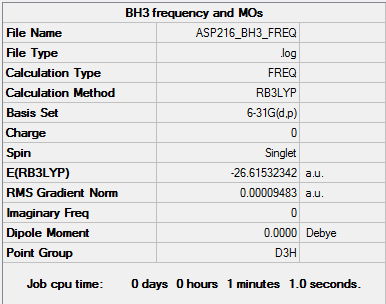
BH3
Optimised borane molecule |
RB3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000190 0.000450 YES RMS Force 0.000095 0.000300 YES Maximum Displacement 0.000747 0.001800 YES RMS Displacement 0.000374 0.001200 YES
Download optimised .log file here
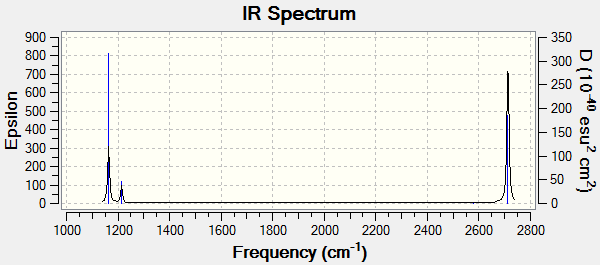
Frequencies
Low frequencies --- -0.2260 -0.1036 -0.0055 48.0278 49.0875 49.0880 Low frequencies --- 1163.7224 1213.6715 1213.6741
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
|---|---|---|---|---|
| 1164 | 92 | A2" | Yes | Bend (out of plane) |
| 1214 | 14 | E' | slightly | Bend |
| 1214 | 14 | E' | slightly | Bend |
| 2580 | 0 | A1' | No | Symmetric Stretch |
| 2713 | 126 | E' | Yes | Asymmetric Stretch |
| 2713 | 126 | E' | Yes | Asymmetric Stretch |
For borane, there are 6 vibrational modes but only 3 peaks are visible in the IR spectrum. The symmetric stretch (ν = 2580 cm-1) is not IR active as the stretch has no change in dipole moment. The two asymmetrics stretches are degenerate (have the same energy) as they vibrate at the same frequency and therefore the peaks overlap to form one. This is also true for the 2 bends (ν = 1214 cm-1).
MOs
There is little difference between the LCAO and calulated MOs. However, the calculated MOs better show the distribution of electron density across the molecule. It can also be seen that the unoccupied real MOs are more diffuse the occupied MOs, which cannot be realised from the LCAO MOs. This suggests that qualitative MO theory (LCAOs) is useful and reliable for occupied MOs, but less accurate for predicting unoccupied MOs.
For the antibonding MOs it can be seen how electron density is directed away from the B–H bond.
Ng611 (talk) 15:40, 29 May 2018 (BST) Good explanation. What can you say about the orbital contributions to the two unoccupied antibonding MOs?
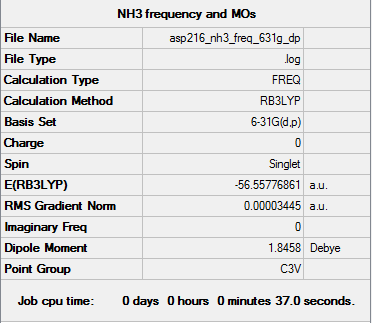
NH3
Optimised ammonia molecule |
RB3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000086 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000315 0.001800 YES RMS Displacement 0.000106 0.001200 YES
Download optimised .log file here
Frequencies
Low frequencies --- -30.2921 -30.2783 -0.0039 0.0080 0.0336 3.6335 Low frequencies --- 1088.7748 1694.0376 1694.0379
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
|---|---|---|---|---|
| 1089 | 146 | A1 | Yes | Bend (out of plane) |
| 1694 | 14 | E | slightly | Bend |
| 1694 | 14 | E | slightly | Bend |
| 3462 | 1 | A1 | No | Symmetric stretch |
| 3591 | 0 | E | No | Asymmetric stretch |
| 3591 | 0 | E | No | Asymmetric stretch |
Ng611 (talk) 15:42, 29 May 2018 (BST) The IR spectrum and table of IR modes isn't necessary here -- don't worry.
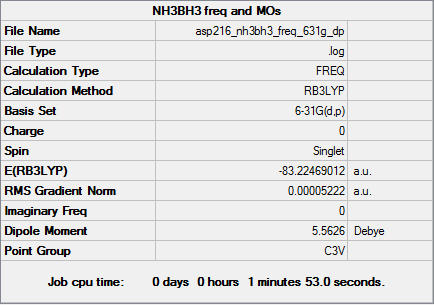
NH3BH3
Optimised ammonia borane molecule |
RB3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000237 0.000450 YES RMS Force 0.000052 0.000300 YES Maximum Displacement 0.001353 0.001800 YES RMS Displacement 0.000365 0.001200 YES
Download optimised .log file here
Frequencies
Low frequencies --- -0.1948 -0.0607 -0.0067 10.8243 16.5775 16.5866 Low frequencies --- 263.0568 631.4015 638.8808
Energy Calculation
E(NH3)= -56.55776861 a.u.
E(BH3)= -26.61532342 a.u.
E(NH3BH3)= -83.22469012 a.u.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE= -83.22469012 - (-56.55776861 + -26.61532342)
ΔE= -0.05159809 a.u. = -135 kJmol-1
The dative bond between B and N in ammonia borane is relatively weak (dissociation energy = 135 kJmol-1), as it is less than that of a covalent C–C bond (350 kJmol-1) in isoelectronic ethane. [1]
Ng611 (talk) 15:42, 29 May 2018 (BST) Good calculation and good comparison, well done!
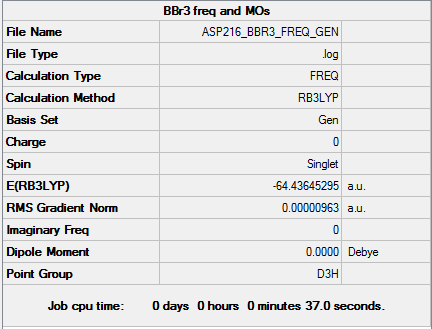
BBr3
Optimised borone tribromide molecule |
B3LYP/6-31G(d,p)LANL2DZ level
Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000090 0.001800 YES RMS Displacement 0.000045 0.001200 YES
Download optimised .log file here
Low frequencies --- -0.0126 -0.0064 -0.0046 2.6412 2.6412 4.9503 Low frequencies --- 155.9599 155.9619 267.6868
Project Section
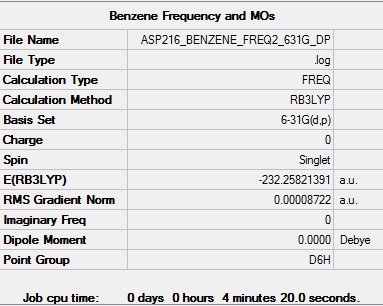
Benzene
Optimised benzene molecule |
RB3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000087 0.000300 YES Maximum Displacement 0.000757 0.001800 YES RMS Displacement 0.000321 0.001200 YES
Download optimised .log file here
Frequencies
Low frequencies --- -2.1456 -2.1456 -0.0088 -0.0042 -0.0041 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
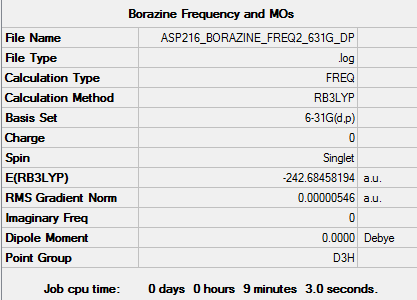
Borazine
Optimised borazine molecule |
RB3LYP/6-31G(d,p) level
Item Value Threshold Converged? Maximum Force 0.000016 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000025 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Download optimised .log file here
Frequencies
Low frequencies --- -13.6679 -13.4715 -10.3782 -0.0099 0.0321 0.0716 Low frequencies --- 289.1330 289.1422 404.0164
Charge Distribution (NBO charge analysis)
| Benzene | Borazine | |
|---|---|---|
 |
 | |
| Charges on atom /e | C: -0.239, H: 0.239 | N: -1.102, B: 0.747, H(–N): 0.432, H(–B): -0.077 |
The above colour scheme ranges from red at a charge of -1.102 and green at 1.102.
Pauling electronegativities: B(2.04); H(2.20); C(2.55); N(3.04)
The distribution of charge in each molecule reflects that molecule's symmetry. In benzene, the D6h symmetry shows all carbon atoms have the same charge. This indicates the covalent nature of the C–C bonds in the ring, as the electron density is evenly spread across the C atoms with no polarised C–C bonds. Conversely, in borazine the nitrogen and boron ring atoms differ in their charge due to the fact that nitrogen is electronegative and boron is electropositive. This distribution follows the D3h symmetry of borazine. The B–N bond is polarised and therefore has some ionic character. These differences electronegativity lead to a lower aromaticity in borazine than in benzene, as electron density is focused more on the nitrogen atoms (more negative charge), reducing the delocalisation of the electrons.[2]
There are different degrees of polarisation between the B–H and N–H bonds, with the N–H bond being more polarised. The greater ionic character shortens (1.097 Å) and strengthens the N–H bond more than the B–H bond (1.195 Å).
Ng611 (talk) 15:48, 29 May 2018 (BST) Very good section and well done for discussing how the symmetry of the two molecules dictates the charge distribution. For borazine, what are the sums of the partial charges for every pair of B-H/N-H?
Both molecules have not overall charge, as the sum of charges of each atom are zero.
MOs
| Benzene | Borazine | Comment |
|---|---|---|
 |
 |
MO22 is one of the degenerate π* LUMO orbitals. This orbital shows some bonding character across two of the C–C/N–B bonds, but is ultimately destabilised by nodes across four of the C–C/N–B bonds leading to overall antibonding character. In borazine, more the lobes are larger on the boron atoms as the energy of the boron based fragment orbitals are closer to the energy of the MO and so have a larger contribution to the MO, due to boron being more electropositive. The benzene MO has e2u symmetry and the borazine MO has e" symmetry. |
 |
 |
MO21 is one of the degenerate π HOMO orbital. This is overall bonding with the lobes spread over ring atoms, but a few nodes along C–C/N–B bonds indicating antibonding character which destabilise the bonding character. In benzene it has e1g symmetry and for borazine it has e" symmetry. In borazine there is a larger contribution to the MO from the nitrogen atoms, evidenced by larger lobes over these atoms. N atoms are more electronegative than B and so its p orbitals are lower in energy, and are therefore closer in energy to the bonding MOs, giving them a larger contribution. |
 |
 |
The MO13 of benzene has b1u symmetry and the MO16 of borazine e1' symmetry. These σ orbitals show only contribution from the fragment orbitals of the H atoms, and are overall non-bonding, with bonding regions between the ring atoms and hydrogens but nodes between the ring atoms themselves lead to antibonding character. There is an equal contribution from each H atom in benzene but, the contributions are larger for H bonded to N and smaller for H bonded to B in borazine. |
Ng611 (talk) 15:59, 29 May 2018 (BST) Good analysis -- some additional comments comparing benzene and borazine would have strengthened this further.
Aromaticity
According to Hückel's rules, cyclic molecules can be classified as aromatic if they:
- They contain 4n + 2 π electrons
- From a contiguous ring of parallel p orbitals
- which are coplanar.
These rules work well for many simple aromatic molecules and are based upon maximising the pi interaction between parallel pz orbitals of the same phase, which allows delocalisation to occur. This is shown in MO17 opposite. In benzene, each carbon atom has one electron situated in the pz and borazine has a lone pair of electrons situated in each nitrogen pz orbital, with the boron pz orbitals empty. Both molecules are isoelectronic and isostructural and obey the 4n + 2 π electron rule (n=1) and are aromatic. As discussed early, borazine is less aromatic then benzene.
However, the rules fail to account for more complex aromatic fused rings. It is clear that this approach doesn't fully and explicitly describe what makes a molecule aromatic. Better considerations of aromaticity are based upon[3]:
- resonance stabilisation energies
- bond lengths of ring atoms between their single and double bond lengths
- considerations of the MOs involved in delocalisation
The delocalisation of electrons allows resonance within the ring. This resonance is found to have a stabilising effect, lowering the energy of the aromatic molecule. For example the energy difference in the hydrogenation of cyclohexene, cyclohexadiene and benzene. The energy for benzene is lower than expected by the trend of the other two. The resonance also produces bonds in the ring that aren't defined single or double bonds, but somewhere in between. This has been shown in the examples opposite where all the bonds within the ring are the same length.
By considerations of the real MOs of aromatic molecules, the behaviour of aromatic molecules can be explained, where valence bond theory fails. It can be seen that aromaticity does not solely arise from delocalisation of π electrons from pz orbitals. The MOs opposite show how in benzene and borazine there is also electron density spread across the molecule in σ MOs, not arising from pz orbitals. This is failed to be accounted for in the simple considerations of aromaticity and Hückel theory.
extra interesting: core orbitals of borazine for boron and nitrogen atoms show the same symmetry as BH3. It is interesting to see how the core MOs of borazine reflect the D3h symmetry fragment s orbitals. The nitrogen based core orbitals are considerably lower in energy than the boron s fragment orbitals. Further to this, these boron MOs are more diffused than the nitrogen MOs.
Ng611 (talk) 15:58, 29 May 2018 (BST) You make some really good points both here and in the previous MO analysis section. Are there any experimental techniques that you could use to assess the degree of aromaticity? What effort has been made in the literature to compare the aromaticity of borazine compared to benzene? What about aromaticity in non planar molecules?
Ng611 (talk) 15:58, 29 May 2018 (BST) Overall this is an excellent report, well done. There were a few minor improvements (which I've highlighted in my individual comments) to be made, and you need to proofread your work more thoroughly. However, overall this was a thorough and well-presented piece of work.