Rep:Mod:asdfghjkl
NH3 Molecule
I've completed an optimization and frequency calculation of Ammonia (NH3), and here are the results and specifications of the optimization:
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy: -56.55776873a.u.
RMS Gradient: 0.00000485a.u.
Point Group: C3v
N-H Optimised Bond Length: 1.01798a.u.
H-N-H Optimised Bond Angle: 105.741 degrees
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986284D-10 Optimization completed.
Molecule
test molecule |
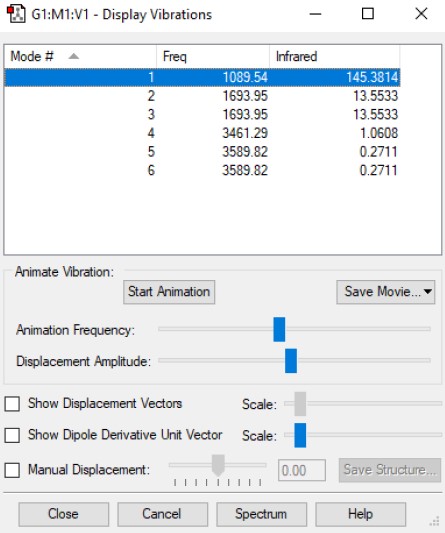
Vibrations
Using the 3N-6, I expect 6 modes, 3(4)-6 = 6
The 2nd and 3rd modes are degenerate. The 5th and 6th modes are degenerate.
Modes 1,2 and 3 are 'bending' vibrations. Modes 4,5 and 6 are 'bond stretch' vibrations.
Mode 4 is highly symmetric.
Mode 1 is the umbrella mode.
I would expect to see 2 bands in an IR spectrum. These are due to modes 1, 2 and 3, where 2 and 3 are degenerate thus form one band, and the modes 4,5 and 6 have too low absorptions to register on the IR Spectrum
Charges
The charges present are:
N = -1.125 eV H = 0.375 eV
I would expect Nitrogen to be negative due to Nitrogen having a significantly higher electronegativity than Hydrogen, drawing the electron density towards it.
N2 Molecule
I've completed an optimization and frequency calculation of Nitrogen (N2), and here are the results and specifications of the optimization:
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy: -109.52412867a.u.
RMS Gradient: 0.00003620a.u.
Point Group: C3v
N-N Optimised Bond Length: 1.10548a.u.
N-N Optimised Bond Angle: 180 degrees
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000063 0.000300 YES Maximum Displacement 0.000020 0.001800 YES RMS Displacement 0.000028 0.001200 YES Predicted change in Energy=-1.228552D-09 Optimization completed.
Molecule
Vibrations
Nitrogen Vibrational Frequency: 2457.51, Infrared : 0.0000
The Bond Mode is a 'bond stretch' vibration, the bond vibration is not visible in the IR Spectrum as there is no change in dipole moment.
Charges
The atoms have no charge as the molecule is diatomic, the electron density is not drawn towards one atom, as the atoms have the same electronegativies.
H2 Molecule
I've completed an optimization and frequency calculation of Hydrogen (H2), and here are the results and specifications of the optimization:
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy: -1.17853936a.u.
RMS Gradient: 0.00000017a.u.
Point Group: C3v
H-H Optimised Bond Length: 0.74279a.u.
H-H Optimised Bond Angle: 180 degrees
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13 Optimization completed.
Molecule
Vibrations
Hydrogen Vibrational Frequency: 4465.68, Infrared : 0.0000
The Bond Mode is a 'bond stretch' vibration
Charges
The atoms have no charge as the molecule is diatomic, the electron density is not drawn towards one atom as the atoms have the same electronegativies.
Reaction Energy
Here I calculate the energy change for the formation of Ammonia in kJ/mol:
N2 + 3H2 -> 2NH3
Energy of the Reaction Products:
E(NH3) = -56.55776873a.u.
2*E(NH3) = -113.1155375a.u
Energy of the Reaction Reactants:
E(N2) = -109.52412867a.u.
E(H2) = -1.17853936a.u.
3*E(H2) = -3.53561808a.u
Energy Change of Reaction:
ΔE = 2*E(NH3)-[E(N2)+3*E(H2)] = -0.05579075 a.u
ΔE = -146.82 kJ/mol (2d.p)
The ammonia product is more stable than the gaseous products. The ammonia product is lower in energy than the gaseous reactants, thus the ΔE for the formation of ammonia is negative, exothermic. The value of ΔE is the energy difference between the reactants and products, the energy released when the product is formed.
Project Molecule - Oxygen
I've completed an optimization and frequency calculation of Oxygen (02) as well as analyzed the MOs, here are the results and specifications of the optimization and analysis:
Calculation Method: B3LYP
Basis Set: 6-31G(d,p)
Final Energy: -150.32004019a.u.
RMS Gradient: 0.00006587a.u.
Point Group: C3v
O-O Optimised Bond Length: 1.21602a.u.
O-O Optimised Bond Angle: 180 degrees
Item Value Threshold Converged? Maximum Force 0.000130 0.000450 YES RMS Force 0.000130 0.000300 YES Maximum Displacement 0.000080 0.001800 YES RMS Displacement 0.000113 0.001200 YES Predicted change in Energy=-1.033738D-08 Optimization completed.
Molecule
test molecule |
Vibrations
Hydrogen Vibrational Frequency: 1642.74, Infrared : 0.0000
The Bond Mode is a 'bond stretch' vibration.
The stretch is not recorded by an IR Spectrum as there is no change in dipole moment for the bond stretch of oxygen.
Charges
The atoms have no charge as the molecule is diatomic, the electron density is not drawn towards one atom, , this is due to the two atoms have the same electronegativities
Molecular Orbitals (MOs)
MO 1.
This is the anti-bonding MO of the 2pz atomic orbitals of the oxygen atoms, it is also the LUMO (lowest unoccupied molecular orbital) of the oxygen molecule. It is relatively high in energy, due to the deep penetration of the 2s orbitals, shielding this orbital resulting in a lower effective nuclear charge. This lower effective nuclear charge means that the electrostatic force of attraction is weaker. The fact that it is an antibond also results in a high energy.
MO 2.
This is the bonding molecular orbital of the 2s atomic orbitals of the oxygen atoms, it is also a fully occupied orbital, containing both electrons. It is relatively low in energy due to its deep penetration resulting in a high effective nuclear charge, however it is still shielded by the 1s orbitals that are significantly lower in energy due to higher penetration. This higher effective nuclear charge results in strong electrostatic forces of attraction between the nucleus and the electrons in the orbital, making it low in energy.
MO 3.
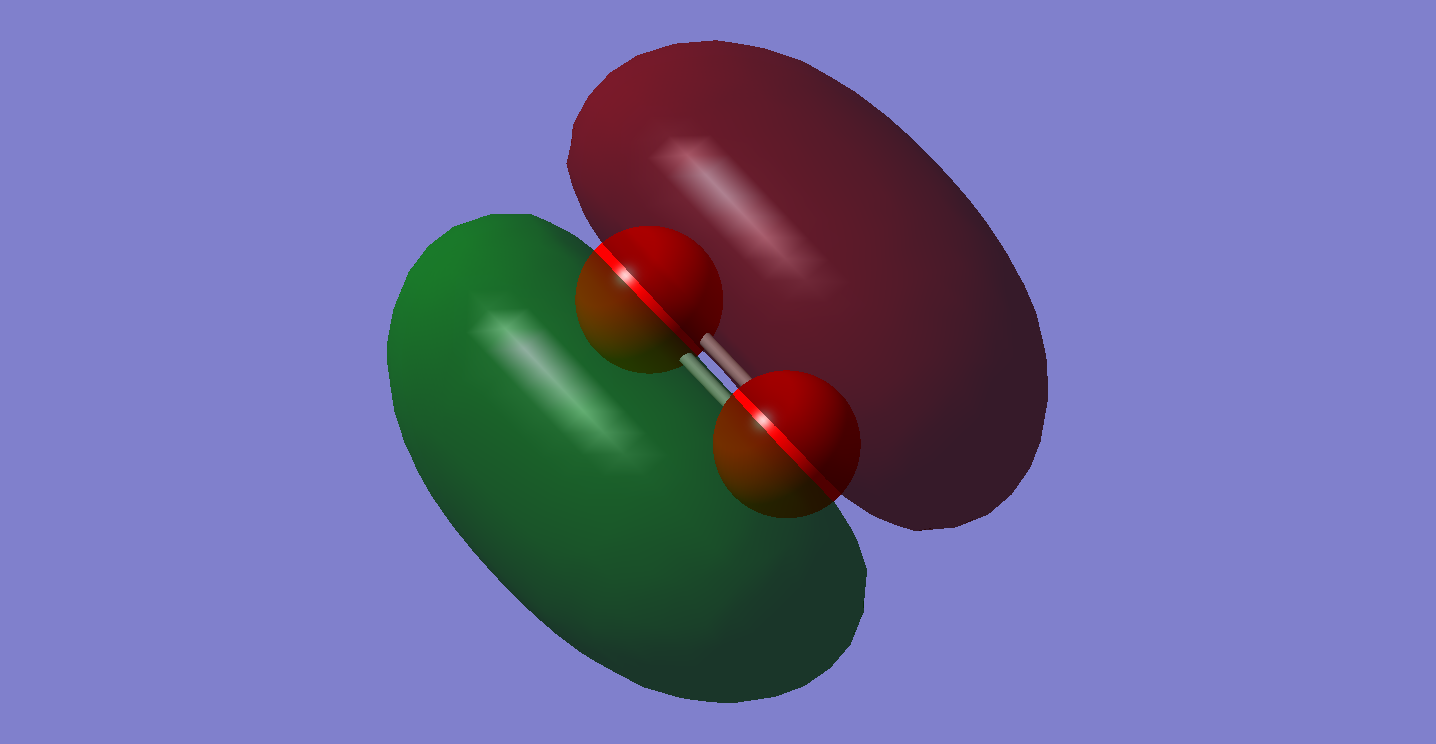
This is the bonding molecular orbital of the 2pz atomic orbitals of the oxygen atoms, it is a fully occupied orbital, containing both electrons. I would expect, due to the fact that this is a bonding orbital, for there to be a greater electron density in between the atoms, whereas in the image the node in between the atoms is smaller than the exterior nodes, this is most likely due to a misrepresentation by the computer program.
MO 4.
This is the bonding molecular orbital of the 2px atomic orbitals of the oxygen atoms, it is a fully occupied orbital, containing both electrons. This molecular orbital is responsible for one of the π bonds present in oxygen molecule, forming one bond of the double bond. The anti-bonding orbital is therefore unoccupied, otherwise the bond would not be present, as once the anti-bonding orbitals are filled the bond dissociates.
MO 5.
This is the HOMO (highest occupied molecular orbital) of oxygen, it is a singularly occupied molecular orbital, resulting in the orbital being especially high in energy. It is the anti-bonding orbital of the 2px atomic orbitals of the oxygen atom. Nodal planes are present in this image of the molecular orbital, these are areas around the molecule where there is no electron density, as the probability of finding electrons in this area is zero.