Jump to content

Rep:Mod:asartor111inorganicproject

From ChemWiki

This is the second half of the writeup for the Year 3 Inorganic Computational experiment. For the first half, see the first wiki page.

Week 2 Mini-Project: NH-Substituted S8 Crowns

A topic encountered in the Year 2 Main Group lecture course was the crown-shaped S8 allotrope of sulfur, as well as a variety of cluster structures containing both sulfur and nitrogen. Housecroft & Sharpe's section on the topic includes a comment regarding the S8 structures, and contains the following statement (emphasis added): "Tetrasulfur tetraimide is one of a number of compounds in which S atoms are formally replaced by NH groups with retention of the crown conformation; S7NH, S6N2H2, S5N3H3 (along with S4N4 and S8)are all obtained by treating S2Cl2 with NH3. No members of this family with adjacent NH groups in the ring are known."[1]

The goals of this project were thus twofold: firstly, to offer a general computational analysis of the structures of NH-substituted S8 crown structures. Second, to investigate whether an explanation could be found for the reluctance of NH groups in these structures towards being adjacent to each other, perhaps in terms of orbital interactions.

The academic literature reports a range of compounds of the type S8-x(NH)x with x taking integer values between 1 and 4. X-ray diffraction studies have shown that all these compounds have structures analogous to the S8 crown structure[2].

To examine possible arguments explaining why no such clusters contained adjacent (NH) groups, several of the crown structures were calculated, using the structure of S8 - which is well defined in the literature - as a starting point. The key comparison was to be between two structures of S6(NH)2; first with the NH groups adjacent (a hypothetical structure not found experimentally), and then with one sulfur atom between the NH groups. This structure, with the nitrogen atoms in the 1,3 positions on the ring, is referred to as 'S6(NH)2 Isomer III' in the literature. Isomers I and II refer to the 1,4 and 1,5 arrangements, respectively.

The rest of this writeup is split into the following sections:

  • General Method: this explains and justifies the method and basis sets chosen for calculations, and outlines the calculations performed
  • Calculation Log: this contains all the output data from every calculation performed
  • Results and Discussion: this contains the analysis of the data gained from the calculations
  • Conclusions: this attempts to answer the initial questions using the information gained, and suggests some topics for further suggestions

General Method

All structures calculated involve only S, N, and H atoms, and so there was no need to use pseudo-potentials at any point. All calculations were performed using the B3LYP method.

S8 was the first structure used for calculations, and it was used as a test for the accuracy/duration trade-off with such calculations. The structure was first roughly drawn to represent the structure reported in the literature, with bond lengths and angles close to that reported. It was then optimised to the 3-21G level, which resulted in a structure that did have the crown arrangement, but with bond lengths and angles significantly larger than experiment. Further optimisation to the 6-31G(d,p) level, with an additional reoptimisation using opt=tight scf=conver=9 int=ultrafine as keywords. Finally, a calculation using the 6-311G(d,p) basis set was performed, as the Gaussian manual reports that this basis set has some improved results for P, S and Cl[3]. This gave a structure resembling experiment much more closely, with bond lengths of 2.10 Å vs. the literature value of 2.06 Å.

As a further check, a similar procedure was followed for S7NH, where one sulfur atom had been replaced by an NH group. Because the two 6-31G optimisation steps for S8 had each taken less than 3 minutes to complete, the decision was made to go straight from the 3-21G output to the 'tight' 6-31G(d,p) step. This took less than 5 minutes. The structure seemed reasonable, although unusual in that the nitrogen atom seemed to have an almost planar geometry rather than the expected tetrahedral one. To see whether the program required a 'nudge' towards a more stable conformer, this geometry was used to make two new geometries; the crown geometry was not changed, but the hydrogen atom was moved so that the nitrogen geometry was tetrahedral. One of these geometries had the hydrogen atom pointing towards the inside of the ring, whereas the other had the hydrogen pointing out. These starting geometries are shown in the calculation log. These were both re-optimised using the same method (tight 6-31G(d,p)) to see whether one of them represented a more stable geometry. However, both were optimised to the same geometry as the initial planar one; it was concluded that perhaps this was the adopted conformation, a feature that was later ratified using MO and NBO analysis. The initially found structure was thus used for a final optimisation to 6-311G(d,p) using the opt=tight scf=conver=9 int=ultrafine keywords.

The optimised S7NH geometry was used as the starting point for the calculations of two isomers of S6(NH)2; one with adjacent NH groups, and one with one S atom between the NH groups. Optimisation straight to the tight 6-311G(d,p) level took less than 15 minutes on HPC, and so the intermediate steps were no longer performed for future calculations.

Using the S8 optimised geometry as a starting point, two new structures were created: S4(NH)4 and (NH)8. (S8 was used as a starting point here rather than S7NH due to the more analogous symmetry). Again, these were performed immediately to the 6-311G(d,p) level; the calculations too less than 30 minutes on HPC.

Finally, H2 and N2 were calculated, as the energies of these molecules were required for discussion. The calculations were performed using the same 6-311G(d,p) basis set to allow for direct energy comparison. Because the molecules are very small, no intermediate less accurate optimisations were deemed necessary. The calculations took less than 20 seconds on HPC.

All calculations were run on HPC and their results are deposited in D-Space. No calculation in this series ever took more than 30 steps to complete. For all final optimisations, a frequency analysis was performed using the same method and basis set. None of these showed any negative low frequencies, suggesting that all optimisations did successfully find minima on the energy surface. Finally, a population analysis was performed on those structures where the results were relevant to the discussion (S7NH, both isomers of S6(NH)2, S4(NH)4, and (NH)8).

Calculation Log

This section is a collection of key data from each calculation: the .log output file, a link to the results on D-space, the results summary table provided by GaussView, and key excerpts from the log file (the convergence check for optimisations, the low frequencies for frequency analyses). All discussion follows in the next section.

In all headings, the phrase "Tight" means the optimisation was run with the keywords opt=tight scf=conver=9 int=ultrafine.

S8

3-21G Initial Optimisation

Files: .log file, D-Space DOI:10042/26221

S8 First Optimisation
File Name ams_s8_opt_321g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 3-21G
Charge 0
Spin Singlet
E(RB3LYP) -3169.8350131 a.u.
RMS Gradient Norm 0.00006935 a.u.
Imaginary Freq
Dipole Moment 0.0024 Debye
Point Group C1
Job cpu time: 0 days 0 hours 2 minutes 41.4 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000112     0.000450     YES
 RMS     Force            0.000051     0.000300     YES
 Maximum Displacement     0.001024     0.001800     YES
 RMS     Displacement     0.000469     0.001200     YES
 Predicted change in Energy=-1.136371D-07
 Optimization completed.

6-31G

Optimisation

Files: .log file, D-Space DOI:10042/26224

S8 Optimisation
File Name ams_s8_opt_631g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -3185.55051597 a.u.
RMS Gradient Norm 0.00004062 a.u.
Imaginary Freq
Dipole Moment 0.0012 Debye
Point Group C1
Job cpu time: 0 days 0 hours 5 minutes 3.5 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000047     0.000450     YES
 RMS     Force            0.000027     0.000300     YES
 Maximum Displacement     0.000191     0.001800     YES
 RMS     Displacement     0.000121     0.001200     YES
 Predicted change in Energy=-2.011161D-08
 Optimization completed.
Frequency Analysis

Files: .log file, D-Space DOI:10042/26233

S8 Frequency
File Name ams_s8_freq_631g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -3185.55051595 a.u.
RMS Gradient Norm 0.00004066 a.u.
Imaginary Freq 0
Dipole Moment 0.0012 Debye
Point Group C1
Job cpu time: 0 days 0 hours 4 minutes 33.4 seconds. 
 Low frequencies ---   -2.3879   -0.0014    0.0012    0.0014    6.3052    6.3302
 Low frequencies ---   71.7033   75.2635  143.5385

6-31G(d,p) Tight

Optimisation

Files: .log file, D-Space DOI:10042/26239

S8 Tight Optimisation
File Name ams_s8_opt_tight_631g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -3185.55050522 a.u.
RMS Gradient Norm 0.00000128 a.u.
Imaginary Freq
Dipole Moment 0.0002 Debye
Point Group C1
Job cpu time: 0 days 0 hours 8 minutes 45.5 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000016     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-1.955993D-10
 Optimization completed.
Frequency Analysis

Files: .log file, D-Space DOI:10042/26242

S8 Tight Frequency
File Name ams_s8_freq_tight_631g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -3185.55050218 a.u.
RMS Gradient Norm 0.00000593 a.u.
Imaginary Freq 0
Dipole Moment 0.0002 Debye
Point Group C1
Job cpu time: 0 days 0 hours 7 minutes 23.7 seconds. 
 Low frequencies ---   -3.7100   -3.7087   -0.3762    0.0026    0.0038    0.0042
 Low frequencies ---   73.0568   73.3118  143.8342

6-311G(d,p) Tight

Optimisation

Files: .log file, D-Space DOI:10042/26240

S8 Tight Optimisation 6311G
File Name ams_s8_opt_tight_6311g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -3185.74562625 a.u.
RMS Gradient Norm 0.00000265 a.u.
Imaginary Freq
Dipole Moment 0.0001 Debye
Point Group C1
Job cpu time: 0 days 0 hours 19 minutes 18.1 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000015     YES
 RMS     Force            0.000003     0.000010     YES
 Maximum Displacement     0.000027     0.000060     YES
 RMS     Displacement     0.000016     0.000040     YES
 Predicted change in Energy=-2.460620D-07
 Optimization completed.
Frequency Analysis
.log output file of final step
Click to load, then right click for options (the first menu option includes animations of all vibrational modes).

Files: .log file, D-Space DOI:10042/26241

S8 Frequency 6311G
File Name ams_s8_freq_tight_6311g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -3185.74562683 a.u.
RMS Gradient Norm 0.00000253 a.u.
Imaginary Freq 0
Dipole Moment 0.0001 Debye
Point Group C1
Job cpu time: 0 days 0 hours 11 minutes 26.5 seconds. 
 Low frequencies ---   -0.0023   -0.0012   -0.0008    2.5390    3.0684    3.0761
 Low frequencies ---   71.3014   71.4381  140.7723

S7NH

3-21G Optimisation

Files: .log file, D-Space DOI:10042/26245

S7NH First Optimisation
File Name ams_s7nh_opt_321g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 3-21G
Charge 0
Spin Singlet
E(RB3LYP) -2828.63028158 a.u.
RMS Gradient Norm 0.00000792 a.u.
Imaginary Freq
Dipole Moment 2.5713 Debye
Point Group C1
Job cpu time: 0 days 0 hours 3 minutes 53.2 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000021     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000229     0.001800     YES
 RMS     Displacement     0.000109     0.001200     YES
 Predicted change in Energy=-6.297552D-09
 Optimization completed.

6-31G(d,p) Tight

Optimisation

Files: .log file, D-Space DOI:10042/26250

S7NH Optimisation
File Name ams_s7nh_opt_631g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.68312603 a.u.
RMS Gradient Norm 0.00000062 a.u.
Imaginary Freq
Dipole Moment 1.8083 Debye
Point Group C1
Job cpu time: 0 days 0 hours 17 minutes 41.6 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000008     0.000060     YES
 RMS     Displacement     0.000003     0.000040     YES
 Predicted change in Energy=-9.104823D-12
 Optimization completed.
Frequency Analysis

Files: .log file, D-Space DOI:10042/26252

S7NH Frequency
File Name ams_s7nh_freq_631g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.68312603 a.u.
RMS Gradient Norm 0.00000062 a.u.
Imaginary Freq 0
Dipole Moment 1.8083 Debye
Point Group C1
Job cpu time: 0 days 0 hours 9 minutes 28.9 seconds. 
 Low frequencies ---   -3.2283   -0.0042   -0.0016    0.0013    2.6187    3.5472
 Low frequencies ---   79.5481   83.4159  150.1490

Alternative geometry check: Hin (6-31G(d,p) Tight)

Starting geometry for "Hin" optimisation, with hydrogen atom bent towards the ring

Files: .log file D-Space DOI:10042/26254

S7NH Hin Optimisation
File Name ams_s7nh_opt_Hin_631g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.68312603 a.u.
RMS Gradient Norm 0.00000087 a.u.
Imaginary Freq
Dipole Moment 1.8083 Debye
Point Group C1
Job cpu time: 0 days 0 hours 22 minutes 28.2 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000018     0.000060     YES
 RMS     Displacement     0.000007     0.000040     YES
 Predicted change in Energy=-2.739800D-11
 Optimization completed.

Alternative geometry check: Hout (6-31G(d,p) Tight)

Starting geometry for "Hout" optimisation, with hydrogen atom bent away from the ring

Files: .log file, D-Space DOI:10042/26260

S7NH Optimisation Hout
File Name ams_s7nh_opt_Hout_631g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.68312603 a.u.
RMS Gradient Norm 0.00000098 a.u.
Imaginary Freq
Dipole Moment 1.8083 Debye
Point Group C1
Job cpu time: 0 days 0 hours 19 minutes 16.5 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000013     0.000060     YES
 RMS     Displacement     0.000006     0.000040     YES
 Predicted change in Energy=-3.456101D-11
 Optimization completed.
Initial optimisation result
Optimisation starting from H "in" geometry
Optimisation starting from H "out" geometry

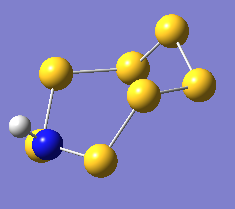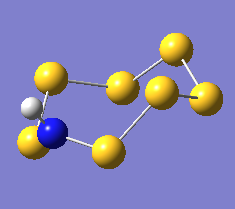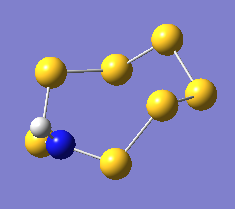The three resulting geometries are shown above, with relevant bond angles and lengths marked in the Jmol applets. The structures are identical.

6-311G(d,p) Tight

Optimisation

Files: .log file, D-Space DOI:10042/26275

S7NH 6311G Optimisation
File Name ams_s7nh_opt_6311g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.87173135 a.u.
RMS Gradient Norm 0.00000169 a.u.
Imaginary Freq
Dipole Moment 1.8198 Debye
Point Group C1
Job cpu time: 0 days 0 hours 16 minutes 23.3 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000033     0.000060     YES
 RMS     Displacement     0.000014     0.000040     YES
 Predicted change in Energy=-1.295693D-10
 Optimization completed.
Frequency Analysis
.log output file of final step
Click to load, then right click for options (the first menu option includes animations of all vibrational modes).

Files: .log file, D-Space DOI:10042/26276

S7NH 6311G Frequency
File Name ams_s7nh_freq_6311g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.87173135 a.u.
RMS Gradient Norm 0.00000161 a.u.
Imaginary Freq 0
Dipole Moment 1.8198 Debye
Point Group C1
Job cpu time: 0 days 0 hours 13 minutes 39.3 seconds. 
 Low frequencies ---   -2.0823   -0.0020    0.0016    0.0018    3.1714    3.6219
 Low frequencies ---   78.0661   82.7076  147.8769
Population Analysis

Files: D-Space DOI:10042/26411

S7NH Pop
File Name ams_s7nh_pop
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2842.87176671 a.u.
RMS Gradient Norm
Imaginary Freq
Dipole Moment 1.8195 Debye
Point Group C1
Job cpu time: 0 days 0 hours 1 minutes 20.3 seconds.

S6(NH)2 - Adjacent N Atoms

6-311G(d,p)

Optimisation

Files: .log file, D-Space DOI:10042/26277

S6(NH)2 Adj 6311G Optimisation
File Name ams_s6(NH)2adj_opt_6311g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2499.98921561 a.u.
RMS Gradient Norm 0.00000195 a.u.
Imaginary Freq
Dipole Moment 2.3349 Debye
Point Group C1
Job cpu time: 0 days 0 hours 35 minutes 48.1 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000028     0.000060     YES
 RMS     Displacement     0.000009     0.000040     YES
 Predicted change in Energy=-1.142901D-10
 Optimization completed.
Frequency Analysis
.log output file of final step
Click to load, then right click for options (the first menu option includes animations of all vibrational modes).

Files: .log file, D-Space DOI:10042/26292

S6(NH)2 Adj 6311G Frequency
File Name ams_s6(NH)2adj_freq_6311g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2499.98921561
RMS Gradient Norm 0.00000193
Imaginary Freq 0
Dipole Moment 2.3349
Point Group C1
Job cpu time: 0 days 0 hours 15 minutes 42.8 seconds. 
 Low frequencies ---   -3.2409   -2.4638   -0.0028    0.0031    0.0034    4.8888
 Low frequencies ---   82.2292   93.7543  152.3586
Population Analysis

Files: D-Space DOI:10042/26392

S6(NH)2 Adj NBO
File Name ams_s6(NH)2adj_nbo
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2499.98916989 a.u.
RMS Gradient Norm
Imaginary Freq
Dipole Moment 2.3357 Debye
Point Group C1
Job cpu time: 0 days 0 hours 1 minutes 19.9 seconds.

S6(NH)2 - Isomer III

6-311G(d,p) Tight

Optimisation

Files: .log file, D-Space DOI:10042/26280

S6(NH)2 Gap 6311G Optimisation
File Name ams_s6(NH)2gap_opt_6311g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2499.99811590 a.u.
RMS Gradient Norm 0.00000387 a.u.
Imaginary Freq
Dipole Moment 2.9522 Debye
Point Group C1
Job cpu time: 0 days 0 hours 32 minutes 5.5 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000009     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000040     0.000060     YES
 RMS     Displacement     0.000017     0.000040     YES
 Predicted change in Energy=-5.668948D-10
 Optimization completed.
Frequency Analysis
.log output file of final step
Click to load, then right click for options (the first menu option includes animations of all vibrational modes).

Files: .log file, D-Space DOI:10042/26293

S6(NH)2 Gap 6311G Frequency
File Name ams_s6(NH)2gap_freq_6311g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2499.99811590
RMS Gradient Norm 0.00000389
Imaginary Freq 0
Dipole Moment 2.9522
Point Group C1
Job cpu time: 0 days 0 hours 16 minutes 5.7 seconds. 
 Low frequencies ---   -5.3609   -4.5789   -4.2218   -0.0028   -0.0021   -0.0019
 Low frequencies ---   88.7031   93.3789  163.4470
Population Analysis

Files: D-Space DOI:10042/26391

S6(NH)2 Gap MO
File Name ams_s6(NH)2gap_mo
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -2499.99804278 a.u.
RMS Gradient Norm
Imaginary Freq
Dipole Moment 2.9523 Debye
Point Group C1
Job cpu time: 0 days 0 hours 0 minutes 52.1 seconds.

S4(NH)4

6-311G(d,p)

Optimisation

Files: .log file, D-Space DOI:10042/26296

S4(NH)4 Gaps Tight Optimisation 6311G
File Name ams_s4(nh)4_opt_6311g_tight
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -1814.25096325 a.u.
RMS Gradient Norm 0.00000068 a.u.
Imaginary Freq
Dipole Moment 4.5282 Debye
Point Group C1
Job cpu time: 0 days 0 hours 51 minutes 32.8 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000029     0.000060     YES
 RMS     Displacement     0.000010     0.000040     YES
 Predicted change in Energy=-6.440519D-11
 Optimization completed.
Frequency Analysis
.log output file of final step
Click to load, then right click for options (the first menu option includes animations of all vibrational modes).

Files: .log file, D-Space DOI:10042/26297

S4(NH)4 Gaps Frequency 6311G
File Name ams_s4(nh)4_freq_6311g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -1814.25096240 a.u.
RMS Gradient Norm 0.00000380 a.u.
Imaginary Freq 0
Dipole Moment 4.5282 Debye
Point Group C1
Job cpu time: 0 days 0 hours 20 minutes 21.3 seconds. 
 Low frequencies ---    0.0014    0.0033    0.0042    5.7001    5.7056    8.0047
 Low frequencies ---  114.1451  126.4151  213.4435
Population Analysis

Files: D-Space DOI:10042/26412

S4(NH)4 Pop
File Name ams_s4(nh)4_pop
File Type .log
Calculation Type SP
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -1814.25093492 a.u.
RMS Gradient Norm
Imaginary Freq
Dipole Moment 4.5278 Debye
Point Group C1
Job cpu time: 0 days 0 hours 1 minutes 16.0 seconds.

(NH)8

6-311G(d,p)

Optimisation

Files: .log file, D-Space DOI:10042/26298

(NH)8 Tight Optimisation 6311G
File Name ams_(nh)8_opt_tight_6311g
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -442.68189274 a.u.
RMS Gradient Norm 0.00000930 a.u.
Imaginary Freq
Dipole Moment 0.0000 Debye
Point Group C1
Job cpu time: 0 days 1 hours 19 minutes 3.8 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000011     0.000015     YES
 RMS     Force            0.000005     0.000010     YES
 Maximum Displacement     0.000010     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-3.341524D-10
 Optimization completed.
Frequency Analysis
.log output file of final step
Click to load, then right click for options (the first menu option includes animations of all vibrational modes).

Files: .log file, D-Space DOI:10042/26299

(NH)8 Frequency 6311G
File Name ams_(nh)8_freq_6311g
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -442.68189776
RMS Gradient Norm 0.00001192
Imaginary Freq 0
Dipole Moment 0.0001
Point Group C1
Job cpu time: 0 days 0 hours 32 minutes 25.0 seconds. 
 Low frequencies ---  -11.3541  -10.8065  -10.7903   -0.0008    0.0008    0.0009
 Low frequencies ---  156.8153  159.0996  295.7789

H2

6-311G(d,p)

Optimisation

Files: .log file, D-Space: DOI:10042/26388

H2 Optimisation
File Name ams_h2_opt_6311G
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -1.17957106 a.u.
RMS Gradient Norm 0.00000026 a.u.
Imaginary Freq
Dipole Moment 0.0000 Debye
Point Group D*H
Job cpu time: 0 days 0 hours 0 minutes 14.7 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000001     0.000060     YES
 RMS     Displacement     0.000001     0.000040     YES
 Predicted change in Energy=-2.784229D-13
 Optimization completed.
Frequency Analysis

Files: .log file, D-Space: DOI:10042/26386

H2 Frequency
File Name ams_h2_freq_6311G
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -1.17957106 a.u.
RMS Gradient Norm 0.00000056 a.u.
Imaginary Freq 0
Dipole Moment 0.0000 Debye
Point Group D*H
Job cpu time: 0 days 0 hours 0 minutes 6.4 seconds. 
 Low frequencies ---   -5.9796   -5.9796   -0.0001   -0.0001    0.0001 4419.2182

N2

6-311G(d,p)

Optimisation

Files: .log file, D-Space: DOI:10042/26390

N2 Optimisation
File Name ams_n2_opt_6311G
File Type .log
Calculation Type FOPT
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -109.55592975 a.u.
RMS Gradient Norm 0.00000001 a.u.
Imaginary Freq
Dipole Moment 0.0000 Debye
Point Group D*H
Job cpu time: 0 days 0 hours 0 minutes 14.3 seconds. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000000     0.000060     YES
 RMS     Displacement     0.000000     0.000040     YES
 Predicted change in Energy=-6.677853D-17
 Optimization completed.
Frequency Analysis

Files: .log file, D-Space: DOI:10042/26385

N2 Frequency
File Name ams_n2_freq_6311G
File Type .log
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -109.55592975 a.u.
RMS Gradient Norm 0.00000118 a.u.
Imaginary Freq 0
Dipole Moment 0.0000 Debye
Point Group D*H
Job cpu time: 0 days 0 hours 0 minutes 10.8 seconds. 
 Low frequencies ---   -0.8019   -0.8019    0.0005    0.0006    0.0006 2447.1164

Results and Discussion

Structures

The geometries of all optimised structures were listed as part of the Calculation Log above, in the form of interactive Jmol applets. This section contains a few particular sets of data extracted from these structures, mostly for the sake of comparison to literature in order to show the calculations' validity.

Literature Comparison

S8
S8 Structure (6-311G(d,p))

The structure of the S8 allotrope is very well defined in literature.

Property Calculated Literature[4]
Bond length 2.11 Å 2.060 ± 0.003 Å
Bond angle 109.1° 108.0 ± 0.7°
Dihedral angle 97.5° 98.3 ± 2.1°

As the table above shows, the calculated geometry matched that reported in the literature well, with all properties lying within 3% of the literature values. This agreement gave confidence to the decision to use the optimised S8 geometry as the starting point for the geometries of S7(NH), S4(NH)4 and (NH)8 - the necessary atoms were replaced, and the optimisation then run to the 6-311G(d,p) level.

S6(NH)2 Isomer III
S6(NH)2 Isomer III Structure (6,311-G(d,p))

As a representative literature comparison of the optimised structures of nitrogen-containing structures, S6(NH)2 Isomer III was chosen, as its crystal structure has been recorded experimentally by X-ray diffraction.

Bond Lengths (Å) Bond Angles (°) Dihedral Angles (°)
Atoms Calculated Literature[5] % difference Atoms Calculated Literature[5] % difference Atoms Calculated Literature[5] % difference
S2-N9 1.70 1.675 1% N9-S3-N7 110.4 110.0 0% S2-N9-S3-N7 93.1 89.0 5%
N9-S3 1.70 1.677 1% S3-N7-S4 126.1 123.2 2% N9-S3-N7-S4 -93.1 -98.4 5%
S3-N7 1.70 1.660 2% S2-N9-S3 126.1 124.7 1% S1-S2-N9-S3 -99.7 -95.4 5%
N7-S4 1.70 1.674 1% N7-S4-S5 108.6 108.6 0% S3-N7-S4-S5 99.7 104.1 4%
S4-S5 2.12 2.052 3% S1-S2-N9 108.6 109.5 1% S6-S1-S2-N9 87.6 92.8 6%
S5-S6 2.11 2.060 3% S4-S5-S6 109.2 108.3 1% N7-S4-S5-S6 -87.6 -86.2 2%
S6-S1 2.11 2.062 2% S5-S6-S1 106.7 105.5 1% S5-S6-S1-S2 -90.4 -95.4 5%
S1-S2 2.12 2.045 3% S6-S1-S2 109.2 106.7 2% S4-S5-S6-S1 90.4 89.8 1%

Generally speaking, the results are very positive. All calculated bond lengths and bond angles are within 3% of the experimental value, and dihedral angles within 6%. Some of the variation can be accounted for by the fact that the experimental data corresponds to measurements performed on a molecule within a lattice, whereas the calculated structure considers a molecule in isolation, and there is thus no distortion due intermolecular interactions in the packed structure. It is evident that the calculations did yield the appropriate general shape - the crown - with similar trends in bond lengths (S-N bonds shorter than S-S bonds) and angles (S-N-S angles significantly wider).

These results are encouraging not only for this particular structure, but for all structures computed as part of this project, as all computations rely on the same combination of elements, method, and basis set.

Structural Features

Structure S-S S-N N-N
Calculated Bond Lengths (Å)
S8 2.11 - -
S7NH 2.12, 2.12, 2.11 1.69 -
S6(NH)2 N-adjacent 2.14, 2.11, 2.10 1.70 1.39
S6(NH)2 Isomer III 2.12, 2.11 1.70, 1.70 -
S4(NH)4 - 1.70 -
(NH)8 - - 1.41
Structure S-S-N S-N-S S-N-N N-N-N
Calculated Bond Angles (°)
S7NH 109.8 126.1 - -
S6(NH)2 N-adjacent 112.5 - 125.8 -
S6(NH)2 Isomer III 108.6 126.1 - -
S4(NH)4 - 125.9 - -
(NH)8 - - - 126.1

All NH-substituted S8 crown structures calculated as part of this project retain the crown conformation of the ring. This consistency in the geometric structures facilitated direct comparison of their electronic structures.

When replacing S atoms with N atoms, this created bond lengths and angles that differed from the pure S8 case. The single bond covalent atomic radii[6] of S and N are 1.02 and 0.75 Å, respectively. From these, expected S-S, S-N, and N-N bond lengths would be 2.04, 1.77, and 1.50 Å. The table on the right shows the calculated bond lengths in the different structures. (In structures with multiple non-equivalent bonds, these bonds are listed in order of decreasing distance from the N atoms.)

All S-S bonds were calculated to be longer than the expected length of 2.04 Å, indicating that the S-S interactions in these structures are weaker than average for covalent sulfur-containing compounds. The NBO analysis performed later revealed that the S orbitals' hybridisation has more p character than expected from sp3 hybrids, and also all S-N bonds examined had a stronger contribution from N than S. These data suggest that the S atoms do not participate in strong bonding interactions and retain some nonbonded character, explaining the extended bond length as the bonds are weaker than normal.

Conversely, the S-N bonds are all shorter than expected, as are the N-N bonds. This is evidence supporting the suggestion made as part of the MO analysis that the N atoms are at least partially sp2 hybridised and there is some delocalisation of the p electrons into the ring system, providing multiple bond character. The bond order of the S-N and N-N bonds is greater than 1, and so the bonds are expected to be shorter than that calculated for a single bond. The sp2 hybrid N hypothesis was later confirmed as part of the NBO analysis.

Both of these show how the geometric and electronic structure of the molecules are intrinsically linked.

To allow for more comparison between structures, the bond angles involving nitrogen are also listed. These can be compared to the 109.1° bond angle in the S8 crown.

Only one angle is smaller than 109.1°: the S-S-N angle in the N-adjacent S6(NH)2 isomer. The presence of two small nitrogen atoms means that in order to close the ring the S atom is forced to contract its bond angle.

Otherwise, nitrogen-containing bond angles are wider than the S8 S-S-S angle. The bond angles around N are generally around 126°, again supporting the view that N is sp2 hybridised in this system. In fact these angles are even slightly wider than the pure sp2 angle of 120°; this is because the N atoms are connected to larger S atoms, and to close the ring the N angles must expand (while the S angles contract).

Conclusions from Structural Analysis

  • The calculations are generally in good agreement with the literature. They tend to slightly overestimate bond lengths (by about 2.5%).
  • The S-S bonds are longer than standard S-S covalent single bonds, suggesting the interaction in the crown structure is quite weak and the S atoms retain some non-bonded character.
  • N-S and N-N bonds are shorter than expected for single bonds, suggesting they have multiple bond character.
  • The bond angles around N atoms also suggest multiple bond character as they resemble that observed in an sp2 hybrid.
  • Substitution of the NH group creates uneven bond lengths around the ring; S-S bonds are longer than S-N bonds, and N-N bonds are particularly short. In order for the ring to still join up, those atoms forming long bonds (S) are forced to contracttheir bond angles, while those forming short bonds (N) expand theirs.

Energies

S6(NH)2

Because the two isomers of this molecule were calculated using exactly the same method and basis set, their total energies can be directly compared. Isomer III is lower in energy by 0.00890029 a.u. or 23.4 kJmol-1. While this does mean that Isomer III is thermodynamically more stable than the N-adjacent isomer, this difference is actually not that significant; given that the N-adjacent has never been found to exist, one may expect it to be significantly less stable! There must thus also be other reasons for the fact that this structure does not form.

(NH)8 → 4N2 + 4H2

The main reason why this purely hypothetical structure was calculated was to offer some more quantitative data of why such structures with direct N-N bonds are unfavourable. The goal was to calculate the energy of its decomposition into elemental hydrogen and nitrogen. The reason this calculation was performed on (NH)8 rather than any of the sulfur-containing structures is that elemental H and N are well-defined, whereas it would be difficult to define the energy of the sulfur product of the other structures' decomposition because it can exist in a range of allotropes.

Both hydrogen and nitrogen exist as diatomic gases in their elemental forms, and so H2 and N2 were calculated using exactly the same method and basis set. The goal was to find the reaction energy of the following reaction:

The reaction energy can be expressed as ΔE = E(products) - E(reactants) = 4*E(N2) + 4*E(H2) - E((NH)8). The following shows the calculated energy values and final reaction energy:

E(N2) = -109.55592975 a.u.

E(H2) = -1.17957106 a.u.

E((NH)8) = -442.68189274 a.u.

ΔE = 4*(-109.55592975) + 4*(-1.17957106) - (-442.68189274) = -0.2601105 a.u. = -682.9 kJmol-1.

While this value is negative, implying that the elemental products are more stable than the ring structure, and quite large in magnitude, it isn't extremely large to the point where it explains why this molecule does not exist. While this calculation gives the enthalpy change of the reaction, it does not consider the change in entropy. Two factors have to be taken into account here: stoichiometry and phase. In terms of stoichiometry, the reaction involves one molecule breaking apart into eight molecules. This is entropically very favourable, as this larger number of molecules has a larger number of degrees of freedom and thus can exist in a larger number of microstates, resulting in a higher entropy. In terms of phase change, the reaction is also very favourable, as the hypothetical starting material - likely a solid, given that all other experimentally determined crown structures in this project are solids at room temperature - forms gaseous products. The molecules have a much greater energy in the gas state, again a function of the number of microstates. Thus both of these factors contribute towards the reaction being extremely entropically favourable.

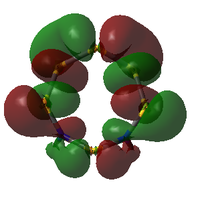
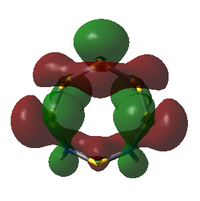
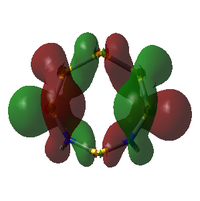
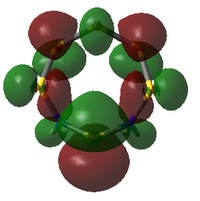
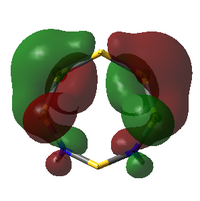
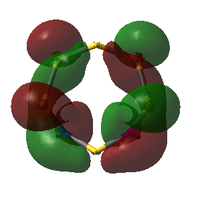
MO Analysis

The molecular orbitals of both isomers of S6(NH)2 were calculated in an attempt to find an explanation of why the structure with the N atoms non-adjacent is preferred.

S6(NH)2 Isomer III

Analysis was limited to the LUMO+1, the LUMO, and all non-core occupied orbitals. Due to the limited time available for this project, the complete set of MOs is listed and described below only for Isomer III. A select few interesting MOs of the other isomer are then directly compared to these in further discussion.

All MOs show the same plane of symmetry across the ring as the molecule itself.

MO Image Comments Occ. Energy
58 This is the LUMO+1. It does show some antibonding character both around the ring, where lobes of opposite phases are close to each other, and across the ring, where lobes on opposite faces are of opposite phase. However, the crown arrangement means there are more in-phase interactions than would be the case were the ring planar. It seems to be built mostly from the p AOs of the ring atoms, but some interaction from the H s AOs is also visible. There is a nodal plane across the ring. 0 -0.076783755
57 This is the LUMO of the molecule. Its buildup appears to be dominated by the half of the ring not containing nitrogen (unsurprising, as nitrogen is more electronegative than sulfur, thus its AOs are lower in energy and contribute less to the higher-energy orbitals and more to those lower in energy). 0 -0.083279593
56 This is the HOMO of the molecule. It appears to be built from the axial p AOs of all ring atoms, with alternating phases, which would give significant antibonding character were the molecule planar, but the crown structure means the lobes have an overal 'sandwich'-like appearance; one phase near the ring, the opposite phase above and below it. The nitrogen atoms are interacting significantly with the sulfur atom between them, with the lobes smeared across this group. This explains the planar geometry of the nitrogen atoms; the N p AOs are delocalised into the ring system, giving the nitrogen atoms aromatic character and stabilising the system. 2 -0.266402105
55 An orbital made up from p AOs of all ring atoms except for the S atom between the N atoms, which seems to be contributing s character. The green 'bridge' lobes connect the N-S-S units, contributing a coherent bonding character to the structure. 2 -0.271060093
54 Similarly to the above orbital, this one contains several 'bridge' lobes connecting groups of 3 or 5 atoms to each other. There is a nodal plane across the ring. 2 -0.272270196
53 The most dominant contribution to this orbital stems from the p AO from the S atom lying between the two N atoms. It shows a favourable overlap with the H s AOs, although the size mismatch between these orbitals means the stabilising effect of this interaction is probably minimal. 2 -0.274761145
52 Contrary to the above, this orbital is mostly located in the non-nitrogen-containing half of the ring, with the large S p AOs overlapping favourably. There is a nodal plane across the ring. 2 -0.284318228
51 Here, the p AOs of the nitrogen atoms are forming lobes reaching around each half of the ring; again this supports the view that delocalisation of the Np orbitals is giving aromatic character, explaining the N atoms' planar geometry. There is a nodal plane across the ring. 2 -0.297996152
50 This orbital also suggests an aromatic-like character throughout the molecule, as both lobes go around the entire ring, with opposite phases above and below them (with the exception of the nitrogen atoms, where the lobe 'reaches around', creating a sandwich-like arrangement, probably causing some through-space antibonding character in the middle of the ring). 2 -0.301855634
49 As above, a molecular orbital showing aromatic character. 2 -0.350086193
48 This orbital seems to be made up from the p AOs of the ring atoms. Because it is quite high in energy the more electropositive sulfur's AOs dominate the contribution. 2 -0.383211592
47 This is another orbital showing interaction between the N p AOs and the S p AOs. There is a nodal plane across the ring. 2 -0.389180049
46 This orbital contains a horseshoe-like lobe in the non-nitrogen-containing half of the ring, providing bonding character not only between adjacent S-atoms but around the ring structure. 2 -0.390151435
45 Another orbital made from p AOs of the ring atoms, with the exception of the S atom lying between the N atoms. It seem to contain a mix of p AOs tangential and axial to the ring structure. There is a nodal plane across the ring. 2 -0.430048331
44 Like orbital 46, this orbital contains significant through-space bonding character in the middle of the ring, to an even greater extent, explaining the lower energy 2 -0.45205701
43 This orbital appears to be made up of tangential p AOs of the ring atoms. The overlap is such that the alternating lobes provide significant sigma bonding character to each pair of adjacent atoms around the ring. There are several intersecting nodal planes across the ring. 2 -0.497471995
42 Here the nitrogen p AOs are overlapping with each other and the intervening S atom, giving bonding character to this N-S-N unit. 2 -0.502196733
41 Contributions to this orbital likely include the H s AO and the N p AOs (in an sp2-like overlap), the tangential p orbital of the S atom in between the N atoms, and axial p orbitals of the two adjacent S atoms. Contributions are more significant from the N atoms than the S atoms, which can be explained by the fact that this orbital is quite low in energy, and thus closer in energy to the N AOs, as N is more electronegative than S and thus its AOs are lower in energy. There is a nodal plane across the ring. 2 -0.55242045
40 Most of this orbital's bonding character stems from an interaction joining together the nitrogen-containing half of the ring. 2 -0.616223147
39 Like orbital 41 in that there are interactions between the N p AOs and the adjacent sulfur atom, but this time the tangential N p AO is used, rather than an axial one. 2 -0.675543449
38 Overlaps between s and tangential p AOs give bonding character to pairs of atoms, particularly the S-S bonds adjacent to the nitrogen atoms, as well as the N-S-N link. 2 -0.681922646
37 Like orbital 38, overlaps between s AOs and tangential p AOs provide bonding character. Here the pattern is regular around the entire ring, stabilising S-S-S, S-S-N, and N-S-N links. 2 -0.777712283
36 The most significant lobes of this orbital involve overlap of two pairs of S s AOs with the p AO of the sulfur atom between them. There is a nodal plane across the ring. 2 -0.791371137
35 The part of the ring not containing nitrogen is enveloped in one lobe of the orbital, while another lobe of the opposite phase is centered around the S atom in between the two N atoms. It likely has contributions from the s AOs of S atoms in the ring, and the p AOs of the N atoms. This orbital again shows delocalisation of the N p AOs, explaining the N atoms' planar geometries. 2 -0.848956636
34 An orbital with one lobe in each half of the nitrogen-containing section of the ring. It likely has contributions from the s AOs of all N and H atoms and the p AO of the S atom between them. It has antibonding character across the ring, but this act over a long distance, while the orbital mainly gives bonding character to the S-S-N links. There is a nodal plane across the ring. 2 -0.938971576
33 A totally symmetric orbital covering most of the nitrogen-containing part of the ring. Being totally bonding, it is unsurprisingly the most stable of the non-core orbitals discussed here. It is likely made up of the s AOs of all N and H atoms, the S atom between them, and the two adjacent S atoms. It contributes significant bonding character to the N-S-N element and may well be part of the explanation for this isomer's stability. 2 -0.979798172

Comparison of Key MOs

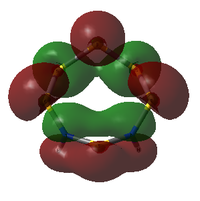
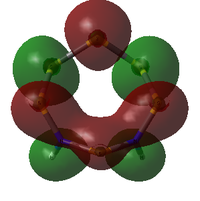
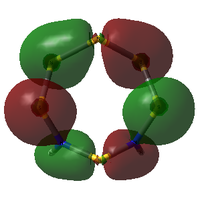
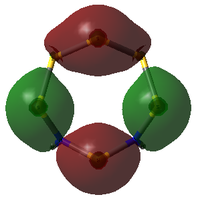
The table below compares some of the key MOs between the two isomers of S6(NH)2. In an effort to maintain legibility, the comments relevant to each pair of MOs are listed below the table rather than as part of it.

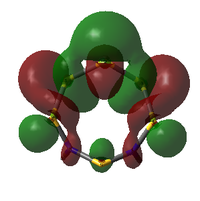
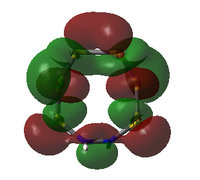
MO Occ. Isomer III Adjacent N
MO Energy LCAO MO MO LCAO MO Energy
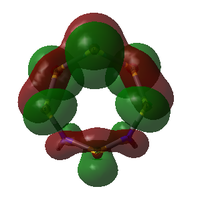
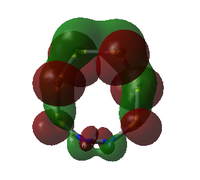
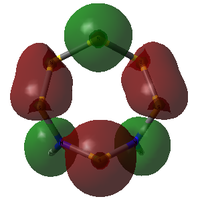
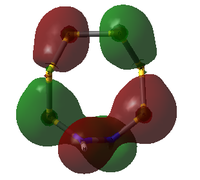
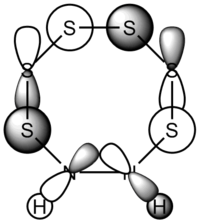
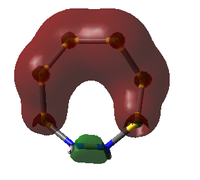
57 0 -0.083279593 -0.091084476
56 2 -0.266402105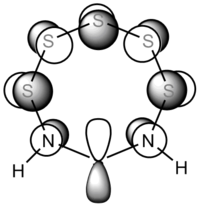
Alternative view here.		 -0.26603255
41 2 -0.552420450
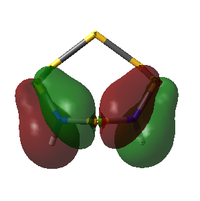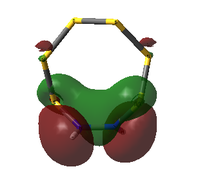Alternative view here.		 -0.558982719
38 2 -0.681922646
Alternative view here.		 -0.694845612
35 2 -0.848956636 -0.856278268
33 2 -0.979798172 -1.039048320

57: The LUMO seems to have a stronger bonding character for the hypothetical N-adjacent structure than for Isomer III, as two lobes span across the ring, giving bonding character. This agrees with the fact that the N-adjacent LUMO is lower in energy, which would likely make this compound more reactive, contributing to the explanation of why it has never been isolated experimentally.

56: The HOMOs of the two molecules are actually quite similar, with the lobes of different phases giving a 'sandwich' appearance when the ring is viewed side-on. What the N-adjacent isomer lacks, however, is a lobe linking together the lower section of the ring; it shows very little bonding character between the N atoms.

41: These orbitals are alike in that the N atoms contribute more significantly than the S atoms for both isomers, indicating the orbital's energy is closer to the lower-energy N AOs than the S AOs. A key difference in the N-adjacent isomer is that the lobes of opposite phase pass diagonally past each other across the ring, and thus are less able to avoid themselves; the visualisation shows them as touching whereas in Isomer III there is a gap between them (although of course this is a function in part of the total electron density cutoff of the visualisation). However, in between the two N atoms there is only one phase, meaning there is significant bonding character between the N atoms. In a way, the orbital could be compared to a N-N π bond that has been twisted and bent. This may suggest that the molecule would prefer to decompose into products containing an N2 atom, where this π bond would be more favoured. The formation of N2 gas would also create a strong entropic driving force. This is another possible explanation for why the N-adjacent isomer does not exist.

38: Both of these orbitals are built up of s orbitals and tangential p orbitals of the ring atoms. The same effect as in orbitals 41 appears; the adjacent N atoms mean that opposite lobes are 'twisted' around each other, like a distorted π bond.

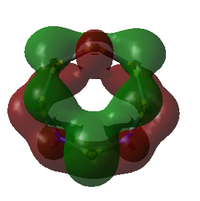
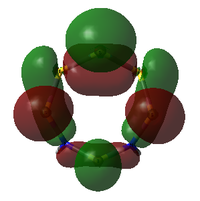
35: These orbitals are similar in that they contain a σ-type 'horseshoe' connecting the upper half of the ring, and a smaller lobe of opposite phase connecting the lower section. In Isomer III, this second lobe combined the N-S-N link, but in the N-adjacent orbital it provides bonding character only between the N atoms, giving significant σ bond character. This again supports the idea that the molecule wants to release a separate N2 atom.

33: These orbitals are again very similar, containing a horseshoe-like σ-type orbital in the lower half of the ring. In the N-adjacent isomer, however, this lobe is smaller, covering only 4 rather than 5 atoms, and so this isomer has less of a coherent bonding nature around the entire ring. The whole ring structure can be considered less likely to be held together.

There is a general trend across the two isomers' MOs suggesting that the N-adjacent isomer's N-N group is more strongly bound to itself than the rest of the ring. Along with the "twisted π"-like orbitals between the N atoms, this suggests that the structure may be inclined to decompose in order to form an N2 atom (which is very energetically stable, and also a gas, providing a significant entropic driving force). The same effect is not present in the isomer where the N atoms are not touching, as the N atoms have less opportunity to communicate directly with each other.

Conclusions from MO analysis

S6(NH)2 Isomer III:

  • The crown arrangement is more stable than a planar arrangement would be, as it avoids a large number of antibonding interactions and instead adopts a 'sandwich' arrangement of the lobes in several MOs.
  • The N p AOs are delocalised into the ring system, giving it "aromatic-like" character. The bonds to N thus are expected to have a bond order greater than 1, and the geometry of the N atoms is closer to planar than tetrahedral.
  • Several bridge-like lobes in different MOs hold together the ring as a coherent hole. Some horseshoe-like lobes also add bonding character across the ring (as well as along it).
  • As expected, contributions are greater from S in the higher-energy orbitals, and greater from N in the lower-energy orbitals.

Comparison of Isomer III with N-adjacent isomer:

  • The HOMO contains only 4, rather than 5, atoms in the N-adjacent isomer.
  • The N-adjacent isomer lacks several "linking" orbital lobes that existed in the N-S-N link of Isomer III.
  • Several orbitals of the N-adjacent isomer contain lobes resembling twisted π orbitals.
  • There is a general trend that in the N-adjacent isomer the N-N link is bonded more strongly within itself than to the rest of the ring, whereas in Isomer III, the N-S-N link is well bound to the ring as a whole.

NBO Analysis

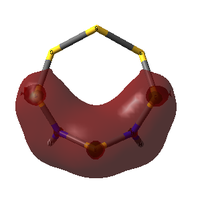
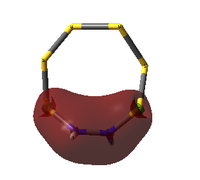
The following shows the charge distributions the two isomers of S6(NH)2, coloured in on a range between -1.000 e (red) and +1.000 e (green):



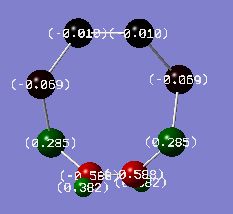N-adjacent S6(NH)2 charge distribution

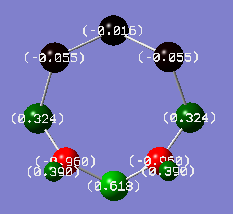S6(NH)2 Isomer III charge distribution

For the sake of comparison, the same analysis was also performed on S7NH, to show the effect experienced by a single nitrogen atom, and S4(NH)4, to show the effect in a ring consisting only of alternating charges. All these calculations were performed using the same method and basis set, and all charge distributions are coloured using the same scale from -1.000 e to + 1.000 e.



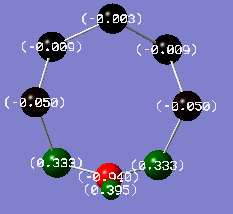S7NH charge distribution

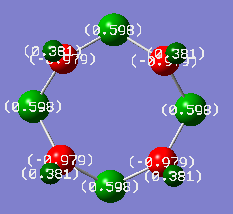S4(NH)4 charge distribution

The following table shows the localised charges. The different S atoms' charges are listed in order of decreasing separation from the N atoms.

Structure Charge on N Charge on H Charges on S
S7NH -0.94 +0.40 +0.33, -0.05, -0.01, -0.00
N-adjacent S6(NH)2 -0.59 +0.38 +0.29, -0.07, -0.01
S6(NH)2 Isomer III -0.96 +0.39 +0.32, -0.55, -0.016
S4(NH)4 -0.98 +0.38 +0.56

The most significant trend is in the charges of the N atoms: it is close to -1 e for all structures except the N-adjacent isomer of S6(NH)2, where it is only around -0.6 e. This is an obvious contributor to the lack of stability of this hypothetical structure; nitrogen is more electronegative than both sulfur and hydrogen and can thus be expected to carry an excess of negative charge, but the extent of this is significantly limited in the N-adjacent case because the adjacent N atoms are competing for electron density to a much greater extent than N atoms separated by more electropositive S atoms. In the non-N-adjacent structures, the negative charge on the nitrogen atoms increases in magnitude as more nitrogen is added to the system. It seems that the alternating geometry is ideal for providing ionic character.

The trend in the charges localised on sulfur is also interesting. In S7NH and S6(NH)2 Isomer III, sulfur atoms on the side of the ring not containing nitrogen actually carry some negative charges. This probably isn't in itself particularly unfavourable, as sulfur isn't particularly electropositive, but it can still be expected that the situation is improved in S4(NH)4 where all of the excess negative charge are carried by N, which is the most electronegative element in the system.

Just like ionic lattices prefer arrangements of alternating cationic and anionic charges, this system is more stable with an alternating δ+/δ- geometry. In the N-adjacent S6(NH)2 isomer, two δ- charges are in direct contact with each other, which is electronically unfavourable.

The NBO analysis also provides information in the form of 2c-2e orbitals between adjacent atoms in the system, giving the relative contribution to the bond from each atom, as well as the contributions of the different atomic orbitals.

The N-adjacent isomer of S6(NH)2 contains only one type of S-N bond (as the two S-N bonds are equivalent by symmetry within the accuracy of this calculation), which has the following NBO: 

     6. (1.98664) BD ( 1) S   4 - N   7 
                ( 35.69%)   0.5974* S   4 s( 13.82%)p 6.16( 85.15%)d 0.07(  1.03%)
                                            0.0000  0.0002  0.3596  0.0943 -0.0006
                                            0.0000  0.0001  0.6899  0.0613  0.0073
                                           -0.0013  0.0000  0.4245  0.0692  0.0065
                                           -0.0005 -0.0001 -0.4315 -0.0221 -0.0068
                                            0.0007  0.0591 -0.0605 -0.0404  0.0355
                                           -0.0157
                ( 64.31%)   0.8020* N   7 s( 28.95%)p 2.45( 70.92%)d 0.00(  0.13%)
                                            0.0001  0.5378 -0.0156 -0.0005 -0.5197
                                           -0.0185  0.0055 -0.6002  0.0120  0.0050
                                            0.2799 -0.0041 -0.0024  0.0275 -0.0104
                                           -0.0145 -0.0046 -0.0124

The bond contribution is 36% from S and 64% from N.

The N orbitals have 29% s and 71% p character, which is halfway between an ideal sp2 and sp3 hybridisation (the former would be 33%/67%, the latter 25%/75%). Meanwhile, the S orbitals have 14% s and 85% p character. This is a very high extent of p character.

To compare, the same analysis was performed on Isomer III of the structure. Here there are two different S-N bonds to consider; that involving the sulfur atom between the two nitrogen atoms (S3 - N7), and that involving the sulfur atom further along the ring (S4 - N7). 

     4. (1.98923) BD ( 1) S   3 - N   7 
                ( 33.42%)   0.5781* S   3 s( 12.80%)p 6.72( 86.04%)d 0.09(  1.16%)
                                            0.0000  0.0001  0.3408  0.1089  0.0003
                                            0.0000  0.0000  0.6945  0.0950  0.0054
                                           -0.0005 -0.0001 -0.4940 -0.0251  0.0021
                                            0.0005  0.0000  0.3518  0.0225 -0.0059
                                           -0.0002 -0.0763  0.0551 -0.0338  0.0280
                                           -0.0283
                ( 66.58%)   0.8160* N   7 s( 33.15%)p 2.01( 66.74%)d 0.00(  0.11%)
                                            0.0001  0.5758 -0.0031 -0.0002 -0.6972
                                           -0.0059  0.0052  0.3046  0.0106 -0.0034
                                           -0.2972  0.0052  0.0010 -0.0202  0.0163
                                           -0.0054  0.0174 -0.0109

Gap outer S-N bond: 

     7. (1.99095) BD ( 1) S   4 - N   7 
                ( 34.46%)   0.5870* S   4 s( 13.56%)p 6.30( 85.38%)d 0.08(  1.06%)
                                            0.0000  0.0001  0.3519  0.1087 -0.0007
                                            0.0000 -0.0001 -0.5118 -0.0391 -0.0057
                                            0.0013  0.0000  0.6105  0.0834  0.0096
                                           -0.0010  0.0000  0.4575  0.0339  0.0051
                                           -0.0010 -0.0669 -0.0492  0.0595 -0.0071
                                           -0.0116
                ( 65.54%)   0.8096* N   7 s( 32.39%)p 2.08( 67.49%)d 0.00(  0.12%)
                                            0.0001  0.5691  0.0020 -0.0002  0.3597
                                            0.0128 -0.0042 -0.6292 -0.0073  0.0041
                                           -0.3865 -0.0011  0.0013 -0.0214 -0.0101
                                            0.0200 -0.0118 -0.0071

The middle S-N bond's N orbitals have 33% s and 67% p character, indicating sp2 hybridisation. The S orbitals have 13% s and 86% p character.

The outer S-N bond is actually very similar. N orbitals are 32% s and 67%p, while S orbitals are 14%s and 85% p.

The strong p character of the S atoms is consistent in all S-N bonds in both structure. The expected N-S-N bond angle could thus be between 109° (sp3) and 90° (p), but this is not the case; the angle is 110.4°. The explanation for this likely lies in the fact that N is smaller than S, and thus the S-N bond is shorter than the S-S bond (1.7 vs 2.1 Å). In order to close the ring with such short links, the angles between the atoms must be widened.

The main difference between the two isomers lies in the N hybridisation; in Isomer III, the N orbitals seem to be purely sp2, whereas in the N-adjacent isomer, they have some sp3 character. The expected effect of this is that the N atoms' geometries are more planar in Isomer III. Visual inspection of the geometries shows that this is indeed the case:

S6(NH)2 N-adjacent S6(NH)2 Isomer III
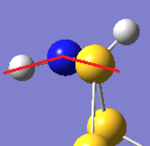
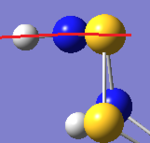
Examining the S6(NH)2 structures, the N atom is more planar in Isomer III than the N-adjacent isomer.

Conclusions from NBO analysis

Charge distributions:

  • The charge distributions show that the nitrogen atoms carry an excess of negative charge. This effect is significantly less strong in the N-adjacent isomer of S6(NH)2 than in other structures examined, because the adjacent nitrogen atoms are directly competing for electron density.
  • Like ionic lattices, the systems prefer an alternating +/- (here δ+/δ-) arrangement. The bonds are polar, and the ionic character can stabilise the molecule as long as the arrangement is sensible and does not contain equal charges in contact with each other (as is the case in the N-adjacent structure).

NBOs:

  • Bonds tend to have stronger contributions from N than S.
  • The N AOs of Isomer III are sp2 hybridised, rationalising the planar structure and supporting the view that these bonds have multiple-bond character because of the delocalisation of the N p orbital.
  • The N AOs of the N-adjacent isomer are between sp2 and sp3 hybridisation. The geometry shows that these atoms are less planar than in the Isomer III case.
  • The S AOs have a p character in excess of 75%, indicating some non-bonded character.

Vibrational Modes and IR Spectra

As well as confirming that all optimised structures were indeed energy minima, the frequency analyses performed also provided information in the form of calculated IR spectra and vibrational modes. A complete set of animations of all vibrational modes can be accessed from the embedded .log file in the calculation log of each molecule; this section discusses a few key modes between different molecules.

The following shows the calculated IR spectra for the two isomers of S6(NH)2:

Calculated IR spectrum of N-adjacent S6(NH)2 (click for full size)


Calculated IR spectrum of S6(NH)2 Isomer III (click for full size)

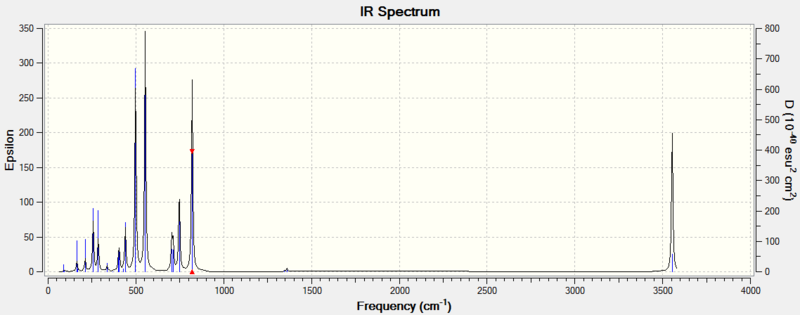
There are two key difference between these spectra: firstly, a peak around 1050cm-1 exists only on the spectrum of the N-adjacent isomer. Secondly, the peak around 800cm-1 is far more intense on the spectrum of Isomer III. The relevant vibrational modes are animated below:

N-adjacent S6(NH)2 S6(NH)2 Isomer III
Mode 20, 1061cm-1 Mode 19, 818cm-1, intensity 5 Mode 20, 820cm-1, intensity 81

Examination of the vibrational mode output shows that the peak at 1061cm-1 in the N-adjacent isomer is due to a mode involving N-N stretching. It is obvious that this mode would not be present in the other isomer, as it has no direct N-N bond.

The modes near 820cm-1 involve the N atoms moving back and forth tangentially to the ring. For Isomer III, the hydrogen atoms remain stationary relative to the nitrogen atoms during this process, whereas for the N-adjacent isomer, they undergo a scissoring motion relative to the N-N bond. This difference in intensity suggests that the vibration causes a greater change in the molecule's dipole moment in Isomer III. Because there is an S atom between the two N atoms in this isomer, the tangential motion is closer to being aligned with the molecule's dipole (which would be drawn as a vertical line on the images above). In the N-adjacent isomer, the N atoms move mostly horizontally as depicted, which is almost perpendicular to the dipole and would thus not affect it very strongly.

For further comparison, the calculated IR spectra of S4(NH)4 and (NH)8 are below:

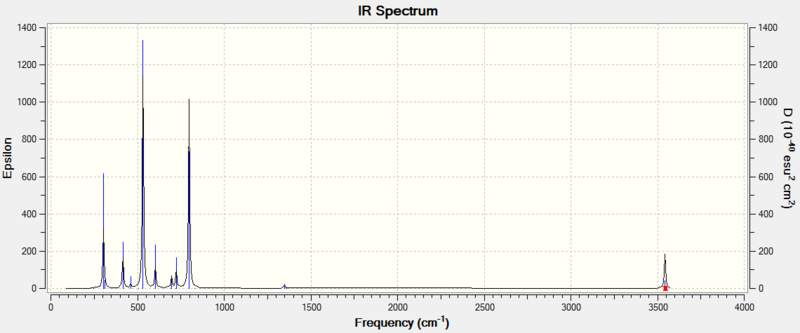
Calculated IR spectrum of S4(NH)4 (click for full size)
Calculated IR spectrum of (NH)8 (click for full size)

A general observation here is that the IR spectra for these compounds show significantly fewer peaks, particularly in the case of (NH)8. This is a function of the increased extent of symmetry of the structures. With a higher symmetry, more of the modes end up not changing the molecule's dipole moment, and are thus IR-inactive.

Like both of the S6(NH)2 isomers, S4(NH)4 contains modes around 800cm-1 where the N atoms are moving tangentially along the ring. However, in S4(NH)4, not all these modes are IR-active. The mode illustrated below, for example, has an intensity of 0. Because of the distribution of N atoms is evenly alternating around the ring, the molecule's dipole is now perpendicular to the plane of the page with the molecule oriented as displayed. This means that the tangential N motions in the plane of the page do not affect the dipole at all.

S4(NH)4 (NH)8
Mode 22, 831cm-1, intensity 0 Mode 19, 1006cm-1, intensity 0

Other than N-adjacent S6(NH)2, the only other ring structure calculated that contains direct N-N bonds was (NH)8. This is the most symmetric molecule of the four discussed here and consequentially has the smallest number of peaks in the IR spectrum. Like before, the N-N bond stretching modes have frequencies around 1000cm-1. The one animated above occurs at 1006cm-1. Unsurprisingly, the intensity of this highly symmetric mode is zero.

Conclusions from Vibrational Analysis

  • The peak at 1061cm-1 in the N-adjacent isomer of S6(NH)2 corresponds to the N-N stretching mode. This peak is not present in the other isomer because it does not contain a direct N-N bond.
  • The peak near 820cm-1 is more intense in Isomer III of S6(NH)2 than in the N-adjacent isomer because the motion is closer to being tangential to the orientation of the dipole, and thus has a greater effect on the dipole moment.
  • The more symmetric structures have simpler IR spectra with fewer peaks, as fewer vibrational modes are IR active.
  • The N-N stretches in (NH)8 occur at a similar frequency than the one observed in N-adjacent S6(NH)2. They are, however, generally IR-inactive, due to the high degree of symmetry in the molecule.

Conclusions

What structures do NH-substituted S8 crowns adopt?

All structures calculated retained the crown arrangement known for the S8 allotrope. Like in S8, the S-S bonds in the structures tend to be slightly longer than is average for S-S covalent single bonds, suggesting that the bonding interactions are somewhat weak. S-N and N-N bonds, however, are consistently shorter than would be expected for covalent single bonds. This is because they possess significant multiple bond character, a conclusion which was also supported by the NBO and MO analysis.

The N atoms have significant sp2 hybrid character and their geometries are thus largely planar. This was explicitly shown for the two isomers of S6(NH)2, where NBO analysis revealed that Isomer III's N atoms were closer to a perfect sp2 hybrid, and the structure revealed that they were indeed more planar than in the N-adjacent case.

A general trend was observed in terms of the bond angles: for the NH-substituted rings, those bond angles around N tended to be wider than ideal considering the hybridisation, while those around S tended to be narrower than observed in S8. Because nitrogen is significantly smaller than sulfur, its bonds around the ring were shorter. In order for the ring structure to still close, the S angles had to be contracted, and the N angles widened.

Why has the S6(NH)2 N-adjacent isomer never been observed?

There are essentially two options here:

  • A: the compound is never formed
  • B: it decomposes too quickly to ever be observed.

These may seem similar, but are distinct when considering what energies are relevant. If the compound is never formed, this means that the energy of the transition state of its formation is so high that none of the starting materials ever adopt this configuration. If the compound is formed but then immediately decomposes, this means that the energy of the transition state of its decomposition is so low that it essentially offers no barrier to the reaction. For both, part of the explanation is likely to be that the relative energy of the crown structure is very high, but the arguments are not identical, as the energy surface either side of this structure's minimum must also be considered.

The first piece of information to consider is thus this relative energy. Calculations showed that the N-adjacent isomer is only 23.4kJmol-1 higher in energy than Isomer III, which is a stable compound. While energetically less stable than Isomer III, this value is too small to be the sole explanation for why the N-adjacent isomer has never been observed under any conditions.

Efforts thus then turned to other methods of analysis in order to better understand the differences between these two structures. A few key observations were made:

  • Examining the structure revealed that the N-N bond in the N-adjacent isomer is shorter than expected for N-N single bonds. NBO analysis showed that the nitrogen atoms in this structure had significant sp2 character, supporting the idea that the N-N bond has multiple bond character.
  • Examining the charge distributions made it clear that the N-adjacent geometry involved δ- charges being directly adjacent. This is electronically unfavourable.
  • MO analysis showed several orbitals of the N-adjacent isomer contained lobes resembling twisted π-type orbitals between the N atoms. This may indicate that it would be preferred by the system to break apart and form an N2 atom, where these π orbitals would not be distorted.

These observations can be broken down into cases supporting arguments A and B:

  • A: The charge distributions suggest that formation of the compound would involve two nitrogen atoms both carrying an excess of negative charge being brought together. This is unlikely for electronic reasons.
  • B: The N-N link is strongly bonded within itself, and contains some twisted π-like orbitals. This suggest that the molecule is inclined to decompose, forming an N2 molecule. This would also be entropically favourable as N2 is gaseous at standard conditions.

Both seem like reasonable explanations for why the structure does not appear to exist. Further study would be required to isolate which of the two effects is the dominant one explaining the phenomenon.

Topics for Further Research

Several topics related to this investigation could be investigated further:

  • To determine whether argument A above is a significant factor, the reactions forming Isomers I-III of S6(NH)2 could be studied computationally. Their transition states may reveal why only three of the four possible structures are observed.
  • To test argument B, a reasonable decomposition pathway of N-adjacent S6(NH)2 could be devised and calculated, offering insight into whether the compound is likely to decompose before ever being observed.
  • Isomers I and II could be calculated in the same way as the N-adjacent isomer and Isomer III were here in order to further quantify the relative instability of the N-adjacent isomer and compare the different structures' MOs.
  • Different ring sizes could be tested to see if the behaviour persists.
  • The structures could be tested with substitutions by heavier elements, e.g. Se instead of S and P instead of N. This may reveal interesting trends.

References

  1. ↑ C. E. Housecroft and A. G. Sharpe, Inorganic Chemistry, Pearson Education Ltd., Harlow, 4th ed., 2012.
  2. ↑ J. C. van de Grampel and A. Vos, Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry, 1969, 25, 611–617. DOI:10.1107/S0567740869002718
  3. ↑ Gaussian Manual: Basis Sets
  4. ↑ B. Meyer, Chemical Reviews, 1976, 76, 367–388. DOI:10.1021/cr60301a003
  5. ↑ 5.0 5.1 5.2 H. J. Postma, F. van Bolhuis, and A. Vos, Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry, 1971, 27, 2480–2486. DOI:10.1107/S0567740871006083
  6. ↑ CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, Boca Raton, 93rd edn., 2012.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:asartor111inorganicproject&oldid=818618"