Rep:Mod:as29

The Cope Rearrangement Tutorial

The objective of this tutorial was to study a chemical reactivity problem and use the outcome of Gaussian calculations to determine the favoured reaction mechanism.

The case study was a [3,3] sigmatropic shift rearrangement, more specifically, the Cope rearrangement of 1,5-hexadiene. The Gaussian calculations enabled us to locate the minima and transition structures on the potential energy surface of 1,5-hexadiene and hence confirm the favoured reaction mechanism.

This rearrangement has been the subject of some controversy over many years concerning its mechanism, hence many experimental and computational studies have been focused around this. The debate of whether it occurs as concerted, stepwise or dissociative seems to have been resolved as it is now generally accepted that the mechanism is concerted, through either a "chair" or "boat" transition state, with the "boat" transition structure lying lower in energy.

Nf710 (talk) 14:16, 3 December 2015 (UTC) Good understanding of the chemistry

Optimising the reactants and products

The Anti2 conformation of 1,5-hexadiene

A molecule of 1,5-hexadiene was drawn on Gaussview, visualised as one of the possible anti-peri-planar conformations, with the dihedral angle set to 180 °. This was then "cleaned" before an optimisation at the Hartree Fock(HF)/3-21G level of theory was run. The energy of this final structure was determined to be -231.69253528 Hartrees, which is in agreement with the reference energy provided in the appendix of the lab script. The symmetrise function was then used, slightly altering the geometry of the structure, confirming that the point group was C_i, as the molecule has a centre of inversion.

Gaussview structure	Point group	Energy/Hartrees HF/3-21G
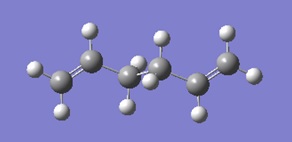
	C_i	-231.69253528

The Gauche4 conformation of 1,5-hexadiene

A Gauche conformer of 1,5-hexadiene was then drawn, with the dihedral angle set to 60 ° this time and was optimised using the HF/3-21G level of theory. The energy was determined to be -231.69153032 Hartrees, which is slightly higher than that of the anti-peri-planar conformer, which was expected due to steric clash of the terminal carbons in the gauche conformer. The point group of this molecule was found to be C₂ after the molecule was symmetrised.

Gaussview structure	Point group	Energy/Hartrees HF/3-21G
	C₂	-231.69153032

The Gauche3 conformation of 1,5-hexadiene

Another gauche conformer of 1,5-hexadiene was drawn, with the aim to find Gauche3 from the appendix of the lab script. The molecule was optimised at the HF/3-21G level of theory again. This structure had a dihedral angle of 67.7 °.

Gaussview structure	Point group	Energy/Hartrees HF/3-21G
	C₁	-231.69266122

The energy was found to be -231.69266122, which was in agreement with the specified energy of the Gauche3 structure. The energy of this gauche conformer was lower than that of the anti-peri-planar conformer. To explain this, the HOMO of Gauche3 was visualised. It can be seen that there is a stabilising interaction between the pi orbitals of the terminal carbon double bonds.

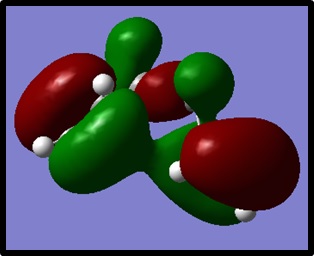
Nf710 (talk) 14:25, 3 December 2015 (UTC)Energies and point groups correct, compared to appendix and very nice use of the orbitals to explain why the gauche is lower in energy.

The re-optimised Anti2 conformation of 1,5-hexadiene

The HF/3-21G optimised Anti2 conformer of 1,5-hexadiene (anti-peri-planar; 180 ° dihderal angle) was re-optimised at the higher DFT/6-21G* level of theory.

Geometry comparison of Anti2 conformer optimised with HF/3-21G and DFT/6-31G*

	C1-C2/C5-C6 (Å)	C2-C3/C4-C5 (Å)	C3-C4 (Å)
HF/3-21G	1.31613	1.50891	1.55275
DFT/6-31G*	1.33350	1.50419	1.54816

Looking at the bond lengths of the anti2 structure at both levels of optimisation, you can see that there is very little difference. Also, the dihedral angle is at 180 ° and the point group is C_i for both conformers. This shows that it is not neccessary to run the optimisation at the higher level of theory.

Frequency calculation of Anti2 conformation of 1,5-hexadiene

Gaussview structure	Point group	Energy/Hartrees DFT/6-31G*	Vibrations
	C_i	-234.61171063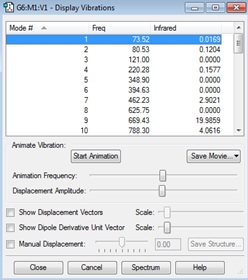

This frequency calculation was run to find the vibrations and confirm that all the frequencies are real and positive so we have found the energy minimum. There are no imaginary frequencies in the IR spectrum, confirming that the minimum was found.

Thermochemistry data

The sum of electronic and zero-point energies: -234.469219 (This was calculated at 0K, whilst the other sums are calculated at 298K)
The sum of electronic and thermal energies: -234.461869
The sum of electronic and thermal enthalpies: -234.460925
The sum of electronic and thermal free energies: -234.500809

Optimising the "Chair" and "Boat" transition structures

In this section, the transition structures of 1,5-hexadiene will be optimised using three methods: Computation of the force constants at the beginning of the calculation; The redundant coordinate editor; QST2. The Intrinsic Reaction Coordinate (IRC) and activation energies are then calculated.

The "Chair"

The "chair" transition structure was optimised using this method. An allyl fragment was drawn and optimised at the HF/3-21G level of theory. The optimised fragment was copy and pasted twice into a new window and the two fragments were orientated to resemble the chair transition state. It was ensured that the terminal carbons of the allyl fragments were 2.2Å apart from each other. This structure was then optimised using two different methods.

Computing the force constant matrix

As we have a reasonable guess for the structure of the transition state, the easiest way to optimise the transition state would be to caclulate the force constant matrix. This only works if we have a reasonable guess for the structure because the reaction coordinate should be easy for the calculation to follow. Problems can occur when the guessed transition state structure is far from the actual transition state structure.

This "guessed" transition state structure is optimised to a transition state (Berny) using a HF/3-21G level of theory with a opt+freq job type. The force constants are calculated once and the keywords "opt=noeigen" are used to stop the calculation crashing if more than one imaginary frequency is found. This is one of the problems that can arise if the guess transition state structure is too far from the exact structure.

Gaussview structure	Vibrations	-817.89cm^-1 frequency animation

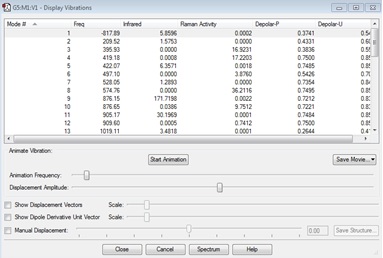
There is only one imaginary frequency found at -817.89cm^-1. This was expected and confirms that the transition state has been found. A negative frequency is linked to a TS because the force constant is negative and this value is square rooted to find the frequency of the motion, hence the imaginary number.^[1] If the vibration is animated, it can be seen that this vibration corresponds to the Cope Rearrangement.

Nf710 (talk) 14:30, 3 December 2015 (UTC) Correct frequency and good understanding of the method

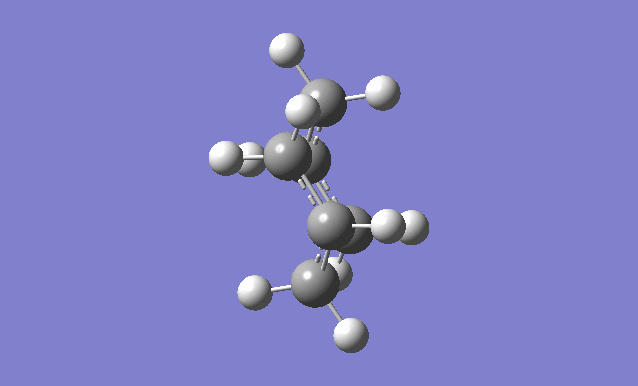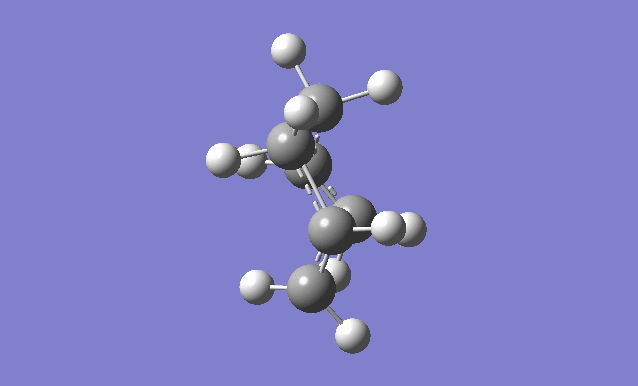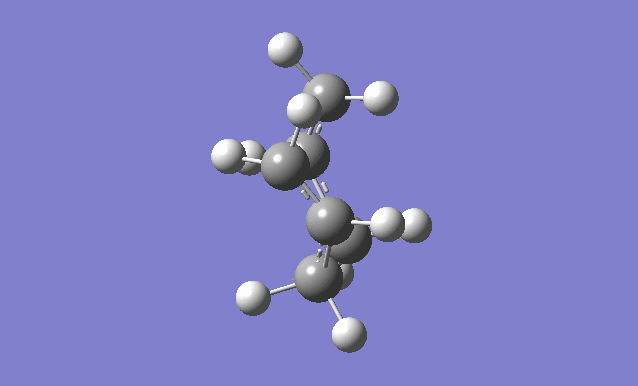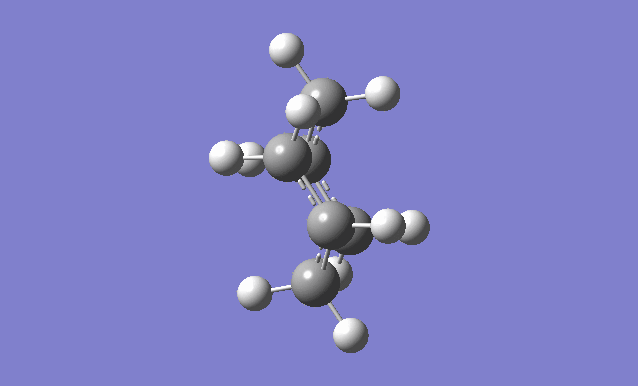
The frozen coordinate method

This method uses the Redundant Coord Editor. First of all, the terminal carbons on the "guess" transition state structure, which break/form a bond during the Cope rearrangement, are selected in the Redundant Coord Editor and the coordinates are then frozen. The distances between these terminal carbons should be set to 2.2Å. This is then optimised to a minimum using the HF/3-21G level of theory.

The chk file is opened and the previously frozen bond forming/breaking distances are now optimised. This is done by running an Opt+Freq with the optimisation going to a TS (Berny) but the force constants are not calculated.

Gaussview structure	Vibrations	-817.86cm^-1 frequency animation

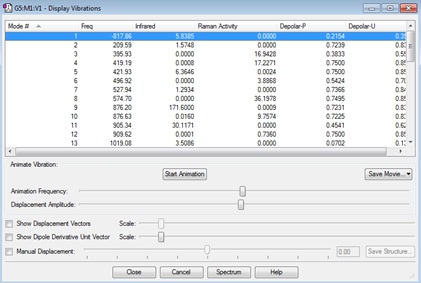
On comparison of this frozen coordinate method with the force constant matrix method, this method is more time consuming and expensive but seems to have better results than just guessing the transition state structure, as problems arise more often. Both final structures had bond breaking/forming distances of 2.0206Å.

The "Boat"

For the "boat" transition state, we used the QST2 method. In this method, the reactant and product structures and atom positions are specified and the calculation tries to find the transition state between them.

The QST2 method

The Opt+Freq calculation is set up, this time optimising to a transition state (QST2) rather than TS (Berny).

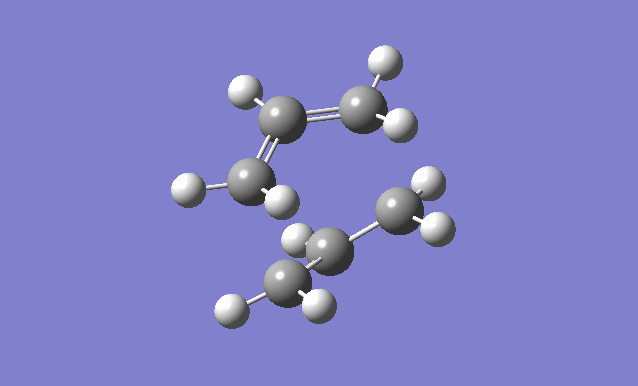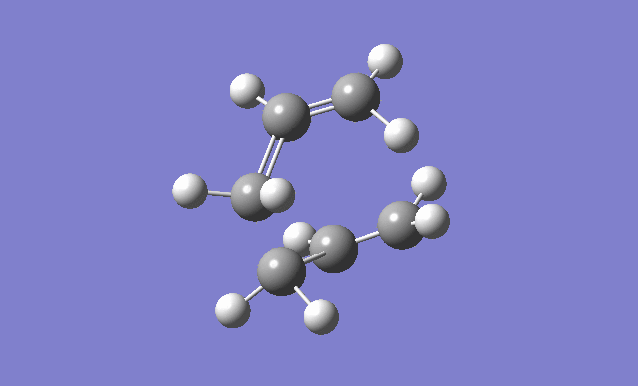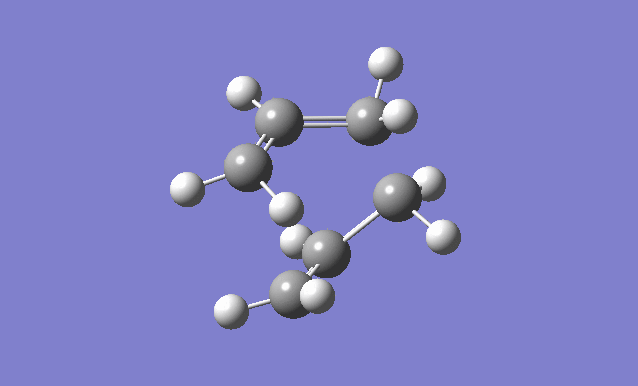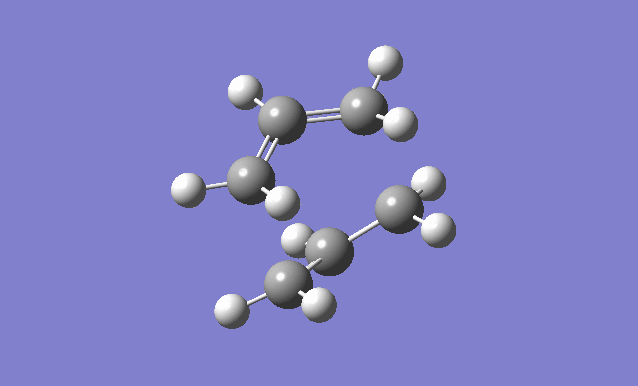
The optimised anti2 conformer of 1,5-hexadiene is used, with the dihedral angles set to 0° and the C2-C3-C4 (reactant) C3-C4-C5 (product) angles set to 100°.

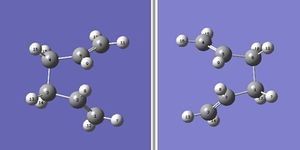
Gaussview structure	Vibrations	-840.22cm^-1 vibration animation

There is only one imaginary frequency at -840.22cm^-1, confirming that the transition structure has been found. When this vibration is animated, you can see that it corresponds to the Cope rearrangement.

Nf710 (talk) 14:34, 3 December 2015 (UTC) Correct energies for both. clearly explained

Intrinsic Reaction Coordinate (IRC)

It is not possible to predict which conformer of 1,5-hexadiene the optimised transition structures will lead to. The IRC method is used as it follows down the reaction path where the gradient is the steepest, hence arriving at the minimum on the potential energy surface from the transition state.

The chair transition state that was calculated using the force constant method was used for the IRC method. The number of points along the IRC was set at 50 steps but the IRC stopped at 44. This is because the minimum had been found, which can be seen from the IRC, where the graph reaches a plateau, so the energy is at a minimum.

IRC	IRC	Reaction path animation

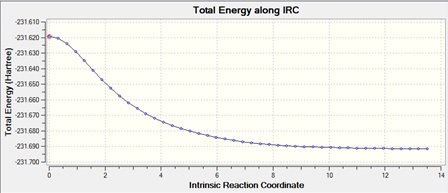
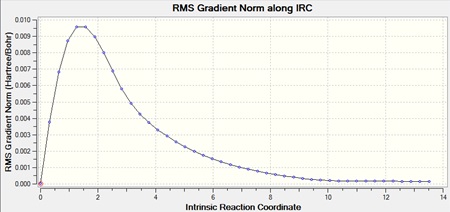
Nf710 (talk) 14:37, 3 December 2015 (UTC) Nice IRC but failed to identify which conf it connects

Activation Energies

Structure	Energy HF/3-21G (Hartrees)	Energy DFT/6-21G* (Hartrees)	Electronic and zero-point energies HF/3-21G (Hartrees)	Electronic and zero-point energies DFT/6-21G* (Hartrees)	Electronic and thermal energies HF/3-21G (Hartrees)	Electronic and thermal energies DFT/6-21G* (Hartrees)
Anti2	-231.69253528	-234.61171063	-231.539539	-234.469219	-231.532565	-234.461869
Chair	-231.61932242	-234.55692628	-231.466700	-234.416255	-231.461341	-234.408999
Boat	-231.60280224	-234.543093	-231.450930	-234.402342	-231.445302	-234.396007

Structure	Activation Energy 298K HF/3-21G (kcalmol^-1)	Activation Energy 298K DFT/6-21G* (kcalmol^-1)	Activation Energy 0K HF/3-21G (kcalmol^-1)	Activation Energy 0K DFT/6-21G* (kcalmol^-1)
Chair	44.7	33.2	45.7	33.2
Boat	54.8	41.3	55.6	42.0

Using a higher level of optimisation is beneficial as the results correspond more closely to those obtained experimentally. ^[2]

Nf710 (talk) 14:53, 3 December 2015 (UTC) Perhaps you ran out of time here. your energies are correct. but you havent compared to experiment. this report could have been improved if you has shown a greater understanding of the theory.

The Diels Alder Cycloaddition

The [4+2] Diels Alder cycloaddition is investigated, using transition state structures and molecular orbital analysis to come to conclusions about its reaction pathway. This concerted reaction involves a diene and a dienophile. In the first case, ethene is the dienophile whilst cis butadiene is the diene. In the second case, cyclohexa-1,3-diene is clearly the diene whilst maleic anhydride is the dienophile, which is made more electron deficient as a result of the electron withdrawing carbonyl substituents. In normal electron demand additions, the diene is electron rich, increasing the energy of its HOMO and the dienophile is electron poor, lowering the energy of its LUMO. This results in better HOMO-LUMO overlap and interaction.

Optimisation of cis butadiene

A molecule of cis butadiene was drawn on Gaussview and optimised using DFT/6-31G*.

(This section should have been done for at least AM1 Tam10 (talk) 15:29, 1 December 2015 (UTC))

The HOMO and LUMO of cisbutadiene are shown below. It can be seen that the LUMO is symmetric and the HOMO is antisymmetric with respect to the plane.

Gaussview structure	LUMO view 1	LUMO view 2	HOMO

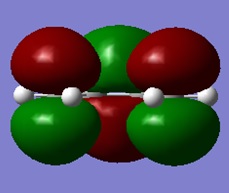
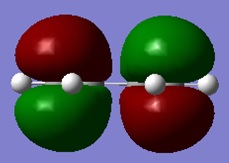
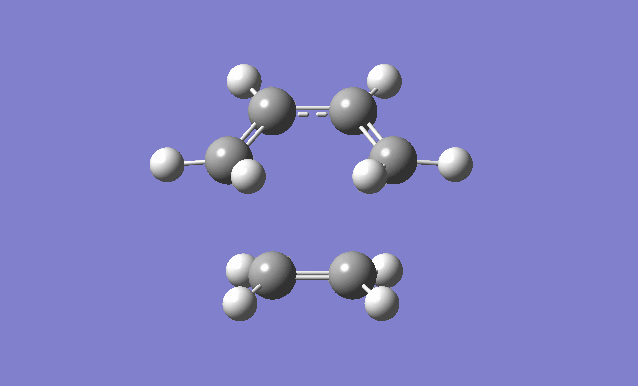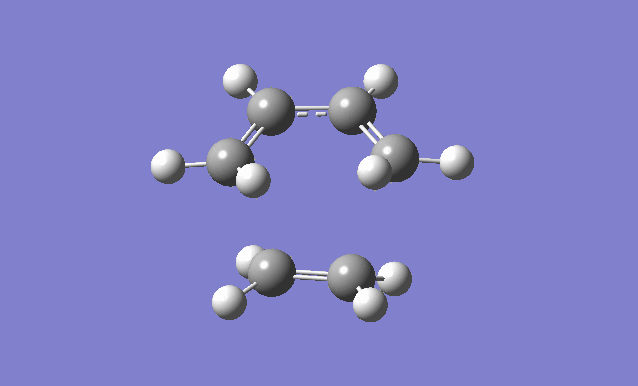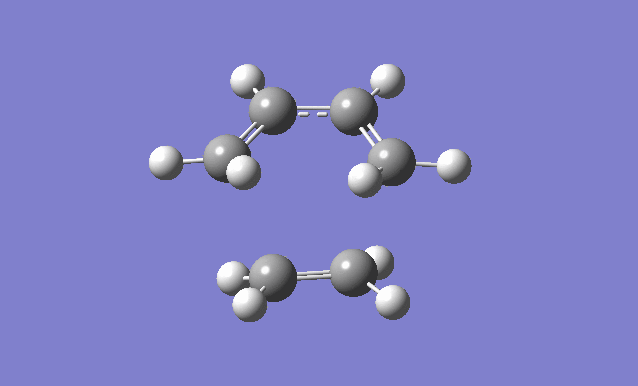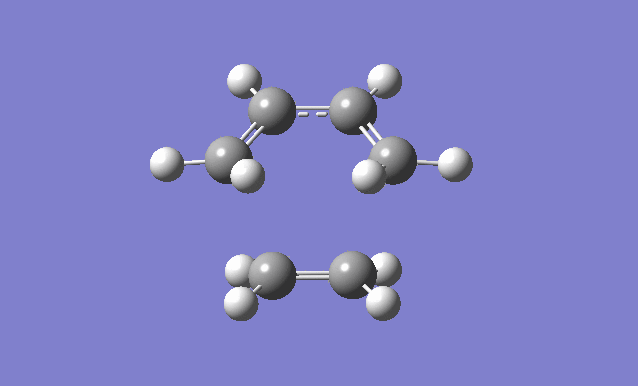
Cis butadiene and ethylene cycloaddition

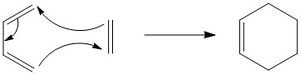
The transition state of the reaction between cis butadiene and ethylene was located, using the force constant method. The optimised cis butadiene was copied onto a new window in Gaussview and the terminal carbon distances between that and ethylene were set to 2.2Å. The symmetry was relaxed and the point group was discovered to be C_s.

It can be seen from the results of the calculation below that the transition state was found as there was only one imaginary frequency, which corresponds to a concerted addition.

Gaussview structure	Antisymmetric HOMO	Symmetric LUMO	Vibrations	-818.40cm^-1 vibration animation	166.59cm^-1 vibration animation

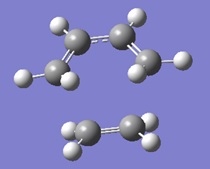
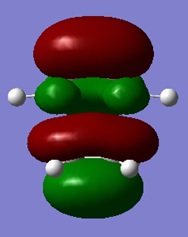
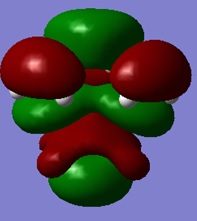
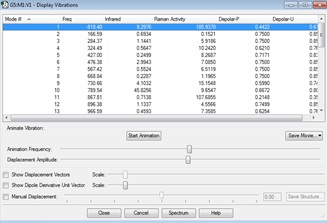
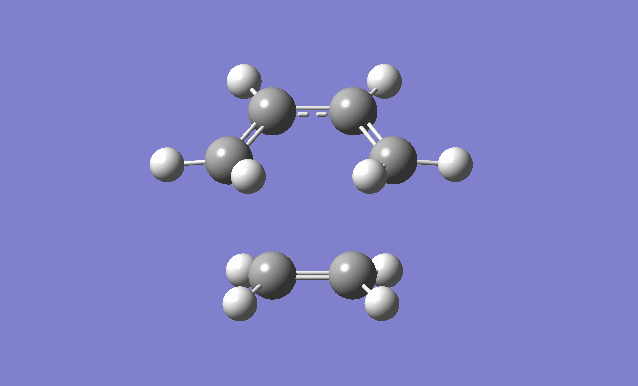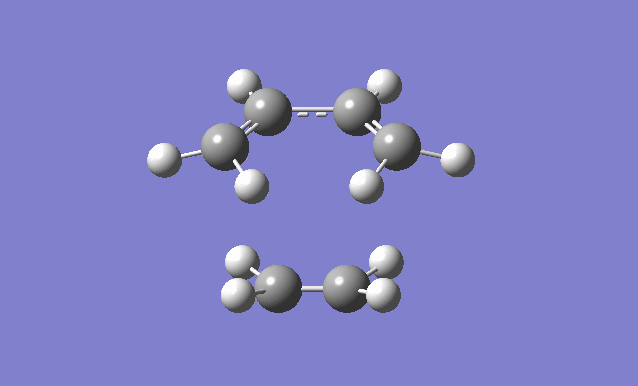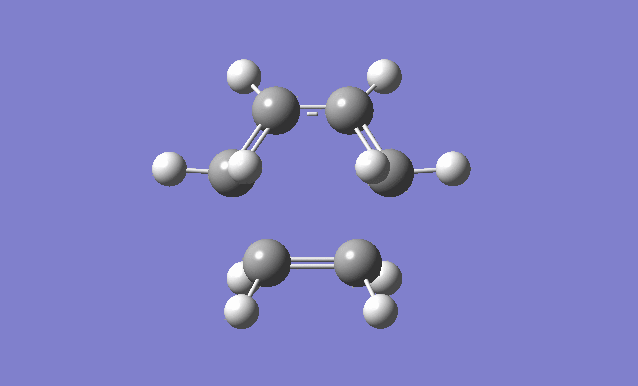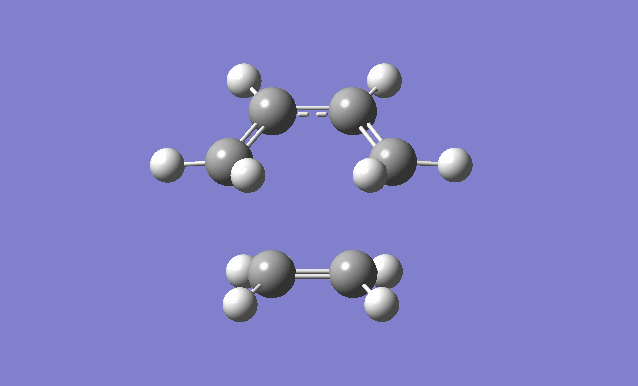
(Earlier you write that your calculations were performed with B3LYP/6-31G(d). These results look like HF Tam10 (talk) 15:29, 1 December 2015 (UTC))

(The HOMO here looks symmetric. This is because you've used HF or B3LYP. The bonding MO in the TS (antisymmetric) is stabilised so much that it is lower in energy than the MO that you've shown. If you used AM1, the MO would be shown as the HOMO Tam10 (talk) 15:29, 1 December 2015 (UTC))

On analysis of the HOMO and LUMO of this system and using the HOMO and LUMO from the optimised cis butadiene, it can be seen that the HOMO of cis butadiene interacts with the LUMO of ethylene to form this TS HOMO.

IRC

An IRC was run from the transition state in both directions, which confirms that there is only one transition state, by analysis of the total energy along the IRC plot. From this, it can also be concluded that this is an early transition state.

(It is the fact that the TS looks like the reactants and the bond-forming lengths are long that indicate it's an early TS Tam10 (talk) 15:29, 1 December 2015 (UTC))

Reaction path

The reaction of cyclohexa-1,3-diene and maleic anhydride

This section is a study of the regioselectivity of the Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride.

Cyclohexa-1,3-diene and maleic anhydride were drawn on gaussview and the structures were optimised using the DFT/6-31G* level of theory.

Cyclohexa-1,3-diene	Maleic anhydride

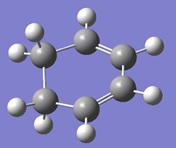
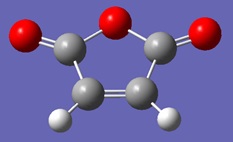
The Exo and Endo transition state structures were then found by using the computation of force constants method, as described previously in section Computing the force constant matrix

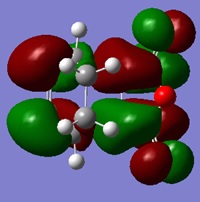
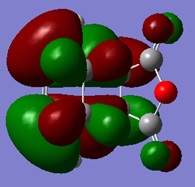
The Exo adduct

Gaussview structure	Energy/Hartrees HF/3-21G	Vibrations	-647.73cm^-1 frequency animation
	-605.60358533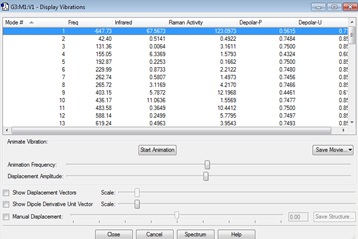

LUMO	HOMO	HOMO -1

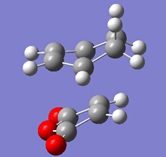
The Endo adduct

Gaussview structure	Energy/Hartrees HF/3-21G	Vibrations	-643.43cm^-1 frequency animation
	-605.61036796

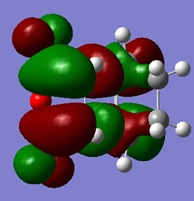
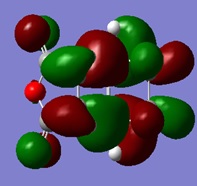
LUMO	HOMO	HOMO -1

In both the Endo and Exo cases, it can be confirmed that the transition states have been found as there is one imaginary frequency and from the animation of these vibrations, it can be seen that this frequency corresponds to the Diels Alder concerted cycloaddition.

From the molecular orbitals shown, it is evident that there are only secondary orbital interactions between the carbonyl of the maleic anhyride and the C-C double bond of the cyclohexa-1,3-diene present in the endo transition state structure. This is simply because the overlap of these orbitals is only possible in the endo TS due to the orientation of the maleic anhydride relative to the cyclohexa-1,3-diene and therefore the distance of the these orbitals.

The energy of the Endo transtion state (-605.61 Hartrees) is slightly lower than that of the Exo transition state (-605.603 Hartrees) and this can be credited to the presence of the secondary orbital interactions in the endo TS. The activation energies could also be calculated here as in the previous tutorial.

(Activation energies would be good to see. Did you run out of time? Tam10 (talk) 15:29, 1 December 2015 (UTC))

The IRCs were run in both directions for both TS structures. It was confirmed that there was only one transition structure in each case.

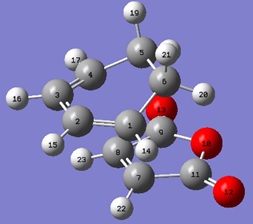
Exo transition structure with labelled atoms

C1-C2 (Å)	C2-C3 (Å)	C3-C4 (Å)	C4-C5 (Å)	C5-C6 (Å)	C1-C6 (Å)	C7-C8 (Å)	C1-C7 (Å)	C4-C8 (Å)
1.36981	1.39762	1.37029	1.51922	1.55873	1.51849	1.37318	2.26389	2.25777

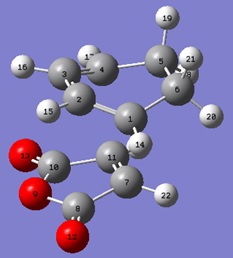
Endo transition structure with labelled atoms

C1-C2 (Å)	C2-C3 (Å)	C3-C4 (Å)	C4-C5 (Å)	C5-C6 (Å)	C1-C6 (Å)	C7-C11 (Å)	C1-C7 (Å)	C4-C11 (Å)
1.37068	1.39662	1.37080	1.51774	1.56016	1.51765	1.37016	2.23196	2.23008

From analysis of the geometries of both the endo and exo transition structures, it can be seen that in the cyclohexa-1,3-diene part of the transition structure, the bond lengths are between that of an sp³C-sp³C single bond(1.54Å) and an sp²C-sp²C double bond(1.34Å). These bonds correspond to those which are either being formed or broken in the cycloaddition. It can also be seen here that the distance between the terminal carbons is less than that of 2 Van der Waals radii, with the distance in the endo TS being smaller than that in the exo TS.

(Can you give an explanation as to why the endo TS C1-C7 length is smaller than exo? What would it infer about the sterics? What about potential steric clashes from H20 and H18(?) with maleic anhydride? Tam10 (talk) 15:29, 1 December 2015 (UTC))

Conclusion

I have successfully used computational chemistry to determine a number of things about a reaction, its mechanism, transition states and reaction pathway. Computational chemistry can be used as a cheap and easy way to visualise reactions. However, it is not always completely accurate and assumptions are made, for example, the Born-Oppenheimer approximation does not take electron-nuclei interactions into account.

In the first section, it was determined that the chair transition state was of a lower energy than the boat transition state, the activation energies were calculated and the reaction pathway was visualised to confirm this. In the second section, it was confirmed that the endo product is regioselectively favoured due to secondary orbital interactions, which could be seen from the computed molecular orbital diagrams.

(Can they be seen? You'd need to be more specific and provide illustrations that show exactly what you're talking about Tam10 (talk) 15:29, 1 December 2015 (UTC))

References

↑ Quantum mechanics 3. Mike Bearpark. Imperial College London 2015
↑ Transition structure lap script. Mike Bearpark. Imperial College London 2015

[1] Quantum mechanics 3. Mike Bearpark. Imperial College London 2015

[2] Transition structure lap script. Mike Bearpark. Imperial College London 2015

[1]

[2]