Rep:Mod:as11815InorganicComp
Inorganic Computational Lab 2nd Year
BH3
BH3 optimisation
freq b3lyp/6-31g(d,p) pop=(nbo,full) geom=connectivity
Item Value Threshold Converged? Maximum Force 0.000185 0.000450 YES RMS Force 0.000080 0.000300 YES Maximum Displacement 0.000769 0.001800 YES RMS Displacement 0.000311 0.001200 YES
Frequency analysis log file ANMOLSADHWANI_bh3_freq_2.log
Low frequencies --- -0.0007 0.0005 0.0005 33.3114 41.6269 43.1791 Low frequencies --- 1163.4848 1213.4697 1213.6151
Optimised BH3 |
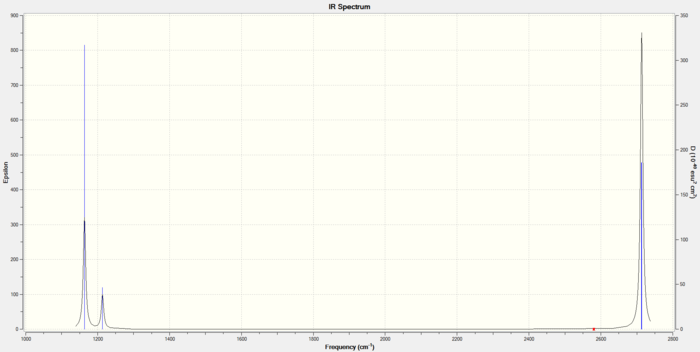
Vibrational spectrum for BH3
| Frequency (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1163 | 92 | A2 | yes | bend |
| 1213 | 14 | E | yes | in-plane symmetric bend (scissoring) |
| 1213 | 14 | E | very slight | asymmetric bend (rocking) |
| 2580 | 0.0056 | A1 | no | symmetric stretch |
| 2713 | 126 | E | yes | asymmetric stretch |
| 2714 | 126 | E | yes | asymmetric stretch |
Ng611 (talk) 16:07, 21 May 2018 (BST) Your two modes at 1213 cm-1 are degenerate -- why therefore would one be slightly IR active, and the other be normally IR active (even their calculated intensities are identical)?
|
There are 6 vibrations. The symmetric stretch is not IR active. This leaves 5 IR active modes; 2 are degenerate pairs. Thus, 3 overall peaks appear in the spectrum.
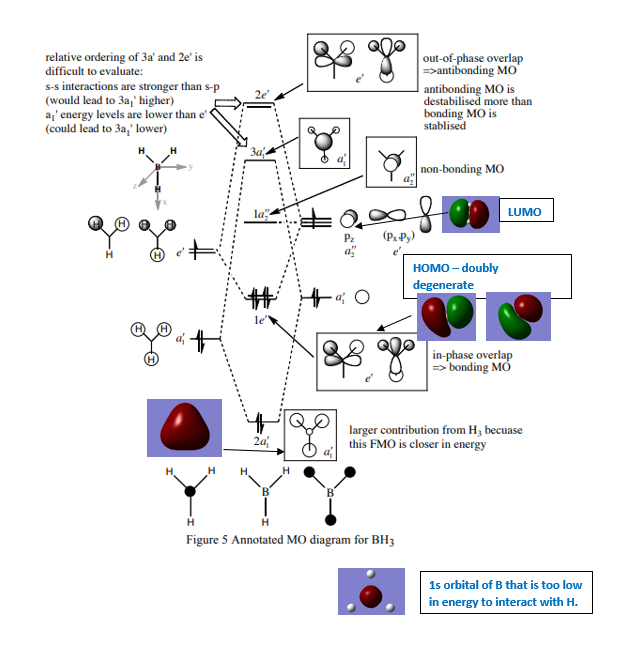
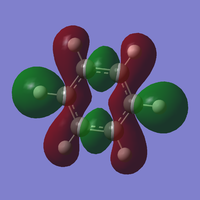
MO diagram for BH3
|
Diagram provided by [[1]]
Ng611 (talk) 16:09, 21 May 2018 (BST) Where are the calculated MOs for your 3a1' and 2e' orbitals?
Differences between predicted from LCAOS and actual MOs: the actual MOs are more diffuse than predicted from LCAO as the electron density is more spread out. LCAO does not give exact solutions for the one electron Schrodinger equation.In quantum mechanics, the variational principle is one method that can be used to minimise the overestimated energy predicted by LCAO. In this case, Gaussian uses the Berny algorithm to minimise the energy of the molecule.
Ng611 (talk) 16:13, 21 May 2018 (BST) The variational principle and Berny algorithm are important aspects of computational chemistry, but they aren't really relevant here. It's also true that the computed MOs are more 'diffuse' than qualitative MOs, but how significant is this difference? Is qualitative MO theory still useful in spite of this?
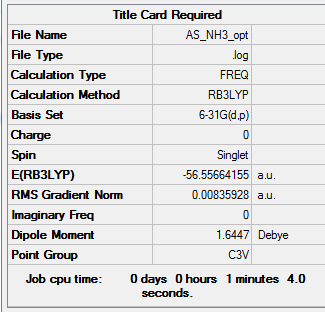
NH3
freq b3lyp/6-31g(d,p) pop=(nbo,full) geom=connectivity
Item Value Threshold Converged? Maximum Force 0.019938 0.000450 YES RMS Force 0.008359 0.000300 YES Maximum Displacement 0.138777 0.001800 YES RMS Displacement 0.048249 0.001200 YES
Frequency analysis log file AS_NH3_OPT.log
Low frequencies --- -426.8524 -426.8509 -385.8927 -0.0077 -0.0012 0.0080 Low frequencies --- 790.4011 1653.0881 1653.0884
Optimised nH3 |
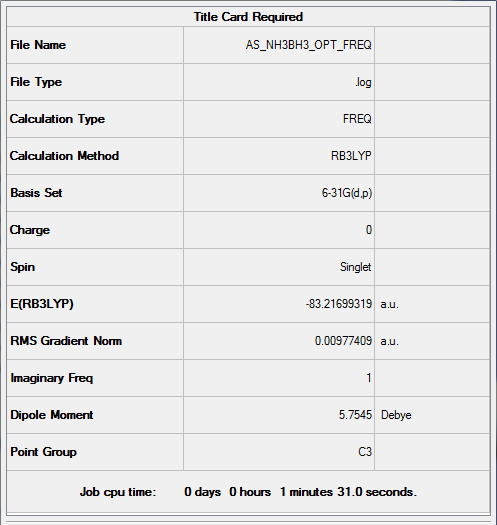
NH3BH3
NH3BH3 optimisation
freq b3lyp/gen pop=(nbo,full) geom=connectivity pseudo=read
Item Value Threshold Converged?
Maximum Force 0.000022 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000106 0.001800 YES
RMS Displacement 0.000051 0.001200 YES
Predicted change in Energy=-2.183749D-09
Optimization completed.
-- Stationary point found.
Frequency analysis log file Media:AnS_NH3BH3_OPT_FREQ.log
Low frequencies --- -426.8524 -426.8509 -385.8927 -0.0077 -0.0012 0.0080 Low frequencies --- 790.4011 1653.0881 1653.0884
Optimised NH3.BH3 |
Link to my completed B3LYP/6-31G(d,p)LANL2DZ BBr3 frequency file: DOI:10042/202391
Calculating the energy stability of NH3BH3 adduct compared with NH3 and BH3
E(NH3)= -56.55664155 a.u. E(BH3)= -26.61532361 a.u. E(NH3BH3)= -83.2169931 a.u.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -0.0405279 a.u.
Ng611 (talk) 16:18, 21 May 2018 (BST) Your energy for NH3 appears to be off somewhat, and this had led to you computing an erroneously small association energy. Good comparisons though -- although try to use literature references (textbooks, papers etc.) rather than websites if you can.
The energy is negative because it corresponds to the association energy of the B-N bond. The energy in J is -102.3734754 kJ/mol. Comparison with a typical strong bond association energy e.g, P=O (-544 kJ/mol) and a weak bond association energy e.g, Sb-Sb (-120 kJ/mol) suggests that the B-N bond is relatively weak.
Energies provided by [[2]]
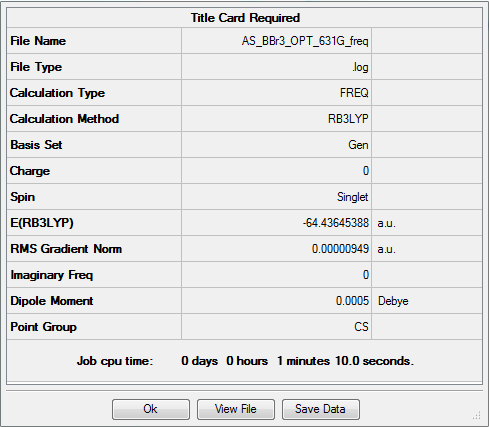
BBr3
freq b3lyp/gen pop=(nbo,full) geom=connectivity pseudo=read
At the minimum of the plateau, there is a change in the bond lengths that cause the symmetry to be point CS instead of C3V. Resymmetrisation could force C3V symmetrisation on the molecule.
Item Value Threshold Converged?
Maximum Force 0.000022 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000106 0.001800 YES
RMS Displacement 0.000051 0.001200 YES
Predicted change in Energy=-2.183749D-09
Optimization completed.
-- Stationary point found.
Frequency analysis log file AS_BBR3_OPT_631G_FREQ.log
Low frequencies --- 0.0002 0.0002 0.0002 1.7808 3.3458 5.1486 Low frequencies --- 155.9469 156.0284 267.7077
Optimised BBr3 |
Dspace link
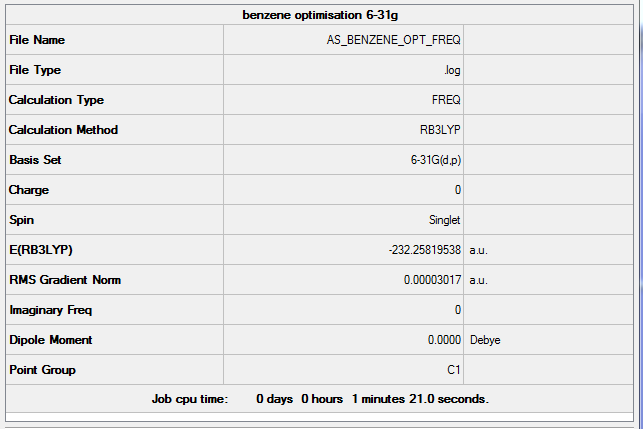
Benzene
freq b3lyp/6-31g(d,p) pop=(nbo,full) geom=connectivity
Item Value Threshold Converged?
Maximum Force 0.000083 0.000450 YES
RMS Force 0.000030 0.000300 YES
Maximum Displacement 0.000275 0.001800 YES
RMS Displacement 0.000107 0.001200 YES
Predicted change in Energy=-3.364544D-08
Optimization completed.
-- Stationary point found.
Frequency analysis log file AS_BENZENE_OPT_FREQ.log
Low frequencies --- -18.4730 -16.7437 -5.3868 0.0005 0.0005 0.0006 Low frequencies --- 414.3521 414.4104 620.8305
Optimised Benzene |
Borazine
freq b3lyp/6-31g(d,p) pop=(nbo,full) geom=connectivity
Item Value Threshold Converged? Maximum Force 0.000238 0.000450 YES RMS Force 0.000083 0.000300 YES Maximum Displacement 0.001909 0.001800 YES RMS Displacement 0.000627 0.001200 YES Predicted change in Energy=-4.146039D-07
Frequency analysis log file AS_BORAZINE_OPT_FREQ.log
Low frequencies --- -15.3820 -7.9095 -0.0001 0.0011 0.0014 8.7511 Low frequencies --- 288.4958 290.1621 404.4042
Optimised Borazine |
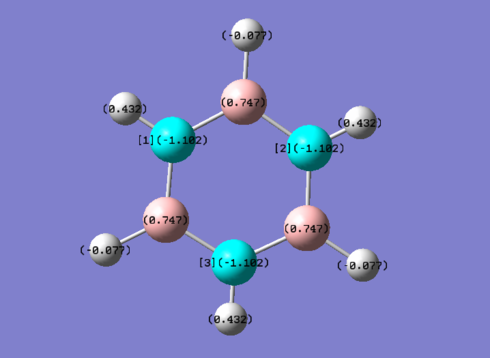
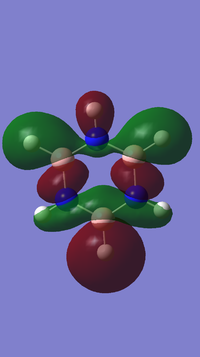
Benzene and Borazine compared
Ng611 (talk) 16:21, 21 May 2018 (BST) Consider tabulating the numerical values of these charges and to use a colour scale for easy visual comparison.
In benzene (left), every carbon has the same electronegativity, resulting in equal partial charge distribution. The hydrogens have an equal and opposite partial charge so that the total charge of benzene is zero. The carbon atoms are more electronegative than hydrogen so these have a negative partial charge while the hydrogens have a positive partial charge.
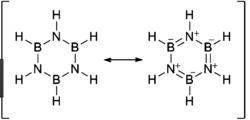
Borazine (right), although isoelectronic with benzene, the different electronegativities give a different charge distribution. The electronegativity of B is 2.04 on the Pauling Scale and N is 3.04. This results in N being more partially negatively charged and B being more partially positively charged which can also be seen in the resonance forms for borazine.
Ng611 (talk) 16:23, 21 May 2018 (BST) Good discussion on electronegativity! I'd add a discussion about how the symmetry of the molecule affects the charge distribution for both benzene and borazine, and perhaps mention something about the sum of partial charges.
Diagram provided by [[3]]
| Benzene | Borazine | MOs compared |
|---|---|---|
 |
 |
Fully bonding MOs. These belong to the lowest energy bonding MO in the Huckel theory of linear atomic combination of p orbitals of ring atoms that give rise to resonance- and in this case aromaticity. There is one nodal plane that coincides with the sigma h plane of the molecules. |
 |
 |
There are 4 nodal planes for both of the MOs. At every atom there is a change of phase but nodes on atoms are less important than nodes between atoms (along the bond). On the atoms the nodes correspond to p orbitals and every bond in the molecule is of a bonding orbital. Thus, these MOs are highly bonding. There is a difference between the two MOs that arise from the fact that the borazine is composed of alternating boron and nitrogens so that there is a difference in how diffuse the bonding orbitals are on either side of the molecule. The B-H bonds are more diffuse than the N-H bonds due to a better orbital match for B-H than N-H. |
 |
 |
There are 2 nodal planes, one matching the sigma h symmetry plane and one sigma v symmetry plane. Only along two of the six resonance bonds is there a change of phase, so the majority of the bonds remain bonding. They match one of the HOMO of the Huckel theory MO diagram for a conjugated pi system. These are bonding MOs. Again, like the example above, there is a slight difference arising from the alternating B, N cyclic structure. the N-B-N orbital overlap is more diffuse because there is more electron density from two lone pairs on the N, compared with the B-N-B orbital overlap. |
Aromaticity Questions
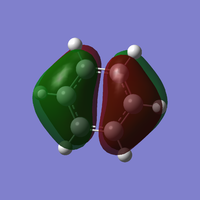
1.) In MO theory, molecular orbitals are formed by taking linear combinations of atomic orbitals. Aromaticity is explained by the extra stabilisation of a cyclic planar molecule that forms resonance bonds. In this case, Huckel theory is used to predict the MOs of pi electrons in conjugated pi systems by simple linear combination of atomic orbitals, as shown in the diagram below.
Diagram provided by [[4]]
These MOs appear in the Gaussian optimisation as the lowest energy 6 occupied MOs for both benzene (6 p orbitals of carbon) and borazine (3 p orbitals form B and 3 p orbitals from N).
2.) Planarity is not required for aromaticity because planarity can be destroyed. The benzene molecule is not planar, it is in a chair conformation due to sufficiently strong intermolecular forces in the lattice structure. There are sigma rings that show aromatisation and 3D structures such as closo-boranes, thus- aromaticity continues being a debatable topic.
Information about aromaticity provided by [[5]]
Ng611 (talk) 16:30, 21 May 2018 (BST) An adequate report. Your charge analysis for benzene/borazine showed promise but needed more detail (remember to discuss things you might think are trivial as it's essential for demonstrating that you've understood the material). Your section on aromaticity was missing a great deal fo detail (how does the modern conceptual picture of aromaticity differ to the earlier views of Huckel etc.? How can aromaticity be validated experimentally?