Rep:Mod:arnv87

Module 3, Experiment 3

The Cope Rearrangement

Optimising the Reactants and Products

		HF/3-21G		B3LYP/6-31G(d)
Conformer	Structure	Summary	Point Group	Summary	Point Group
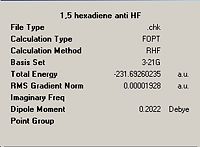
Initial anti, anti1 DOI:10042/to-1448	Pentahelicene		C2		C2
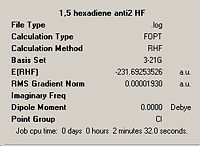
Lowest energy anti, anti2	Pentahelicene		Ci		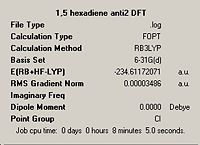Ci
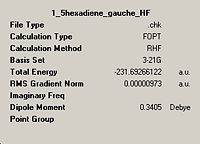
Lowest energy gauche, gauche3 DOI:10042/to-1449	Pentahelicene		C1		C1

While the geometries of each conformer was the same for both levels of optimisation, the energies are different. The gauche conformer was expected to be the higher energy one but this is not the case for the HF optimisation. The B3LYP optimisations however gave the expected result.

Ordering of conformers from lowest to highest energy

HF/3-21G	B3LYP/6-31G(d)
Gauche3	Anti1
Anti1	Anti2
Anti2	Gauche3

The re-ordering of the energies can be explained by comparing the changes in dihedral angle.

	HF/3-21G	B3LYP/6-31G(d)	% Difference
Anti1	-176.875	-176.528	0.20
Gauche3	67.671	66.307	2.02
Anti2	180	180	0

The gauche3 conformer has the largest change in dihedral angle therefore would expect the largest change in energy for this conformer. The dihedral angle for the gauche3 becomes smaller going from the HF to B3LYP optimisation, so the energy increase becomes larger hence the gauche3 conformer becomes the highest energy conformer.

Thermochemistry

	Zero point vibrational energy/kcalmol-1	Sum of electronic and zero-point Energies/HF	Sum of electronic and thermal Energies/HF	Sum of electronic and thermal Enthalpies/HF	Sum of electronic and thermal Free Energies/HF	Zero point vibrational energy/HF	Electronic energy/HF
Anti2, HF	96.00558	-231.539541	-231.532566	-231.531622	-231.570918	0.152994746	-231.692536
Anti2, B3LYP	89.43403	-234.469198	-234.461862	-234.460918	-234.500723	0.142522306	-234.61172

The electronic energy at 0K can be found by subtracting the zero point vibrational energy (which is converted from kcal/mol to HF) from the Sum of electronic and zero-point energies.

Optimising the "Chair" and "Boat" Transition Structures

Chair Transition State Optimisation - Computing Force Constants

The guess chair transition state had an optimisation and frequency calculation run on it using TS(Berny). An additional keyword Opt=NoEigen was entered which prevents the calculation from stopping if more than one negative vibrational frequency is found. The optimisation gave a transition state with an imaginary frequency of -817.953cm^-1.

Optimising Chair Transition State using Frozen Coordinate Method

Using the guess transition state structure, the bonds that form during the rearrangement are frozen. This is done by editing the coordinates of the terminal carbon atoms of each allyl group using the Redundant Coordinate Editor and selecting Bond and Freeze Coordinate after selecting each bond forming carbons. The bond length is set to 2.2Å. Then, the structure is optimised to a minimum. After the optimisation, the bonds are unfrozen, again using the Redundant Coordinate Editor but replacing the Freeze Coordinate option with Derivative. The calculation run is an optimisation to a TS(Berny) but with no force constants calculated.

	Calculating Force Constants	Redundant Coordinates
jmol	Pentahelicene	Pentahelicene
Allyl bond angle/°	120.505	120.505
Partially formed C-C bond length/Å	2.02038	2.02090
Energy/HF	-231.6193224	-231.6193224

The optimised transition state obtained here is similar to the one obtained by computing force constants. The bond lengths, bond angles and energies are also similar for both methods.

Boat Transition State Optimisation - QST2 Method

The QST2 method requires both the reactant and product of the reaction to be specified in the calculation so that the transition state between both can be found. However, using the normal anti2 structure gives a failed calculation as both the reactant and product are not close enough to the transition state for the calculation to find the boat transition state. Hence the reactant and product geometries have to be modified before running the calculation. An opt+freq calculation was run on the modified structures using TS(QST2) and an optimised transition state obtained with an imaginary vibrational frequency of -839.577cm^-1.

Pentahelicene

Optimising boat and chair TS using IRC method

IRC run in the forward direction, with force constants calculated once, 50 points. However, after 50 points, the transition state structure still has not reached its minimum geometry so 3 further calculations were run to determine the minimum geometry.

a) The last point on the first IRC was taken and a normal B3LYP/6-31G* optimisation run. This calculation gave the minimum geometries for the two irc jobs (jmols shown below).

b) A new IRC calculation started with a larger number of points (100 points). This calculation gave the same result as the IRC run with 50 points, ie the transition state still did not reach its minimum geometry.

c) New IRC calculation with force constants calculated always at every point. This calculation failed.

Chair TS Reactant, gauche2 DOI:10042/to-1450	Boat TS Reactant, gauche3 DOI:10042/to-1451
Pentahelicene	Pentahelicene

From the three different methods, I have established that my preferred method of obtaining the reactant or product of a reaction using IRC is to calculate the starting IRC using a certain number of steps (50 or 100) with force constants calculated once, and then to optimise the final IRC geometry using B3LYP/6-31G*.

Reoptimisation of transition structures using the B3LYP/6-31G*

The chair and boat transition state structures optimised using HF/3-21G were reoptimised using B3LYP/6-31G(d) and their geometries and energies compared.

Published Chair TS B3LYP: DOI:10042/to-1452 Published Chair TS B3LYP: DOI:10042/to-1453

	Chair HF/3-21G	Chair B3LYP/6-31G(d)	Boat HF/3-21G	Boat B3LYP/6-31G(d)
Allyl bond angle/°	120.55	119.954	121.701	122.27
Partially formed C-C bond/Å	2.02038	1.96756	2.14015	2.20664
Energy/HF	-231.6193224	-234.556983	-231.6028022	-234.5430931

The geometries of the structures did not change but there is a difference in energy going from HF to B3LYP.

Activation Energy

	HF/3-21G		B3LYP/6-31G*		Experimental
	at 0K	at 298.15K	at 0K	at 298.15K	at 0K
Chair Activation Energy (kcal/mol)	45.71	44.69	34.05	33.17	33.5 ± 0.5
Boat Activation Energy (kcal/mol)	55.60	54.76	41.95	41.32	44.7 ± 2.0

The calculated chair and boat activation energies match the experimental activation energies at 0K. The chair TS activation energies are lower than the boat TS activation energies because all of the atoms in the boat TS are eclipsed.

The Diels Alder Cycloaddition

The calculations were run using AM1 and then B3LYP/6-31G*

Cis butadiene

The HOMO of cis-butadiene is anti-symmetric with respect to the reflection plane while the LUMO is symmetric.

cis butadiene HOMO, antisymmetric

cis butadiene LUMO, symmetric

Ethylene + cis butadiene transition structure

Published B3LYP TS: DOI:10042/to-1454

The method used to find the transition state was computing force constants once at the beginning of the calculation.

jmol	Partially formed C-C bond distance/Å	HOMO	LUMO
Pentahelicene	2.27254	cis butadiene + ethene ts HOMO, antisymmetric	cis butadiene + ethene ts LUMO, symmetric

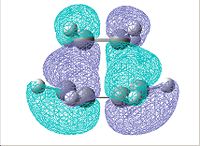sp3 C-C bond length 1.54Å

Imaginary frequency of -524.778cm^-1

sp2 C-C bond length 1.33Å

van der Waals radius 1.70Å

The partially formed bonds are much larger than typical sp3 and sp2 bond lengths therefore it is impossible for a σ-bond to form. However the distance between the bond forming atoms is smaller than the combined Van der Waals distance (1.70Å x 2 = 3.40Å) indicating that the atoms are close together enough for a partial bond to form.

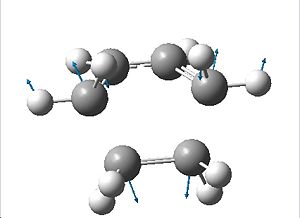
All of the positive frequencies have no relationship with the vibration that corresponds to the reaction path at the transition state. The vibration which does is the negative imaginary frequency. As shown in this vibration, the formation of the two bonds is synchronous.

Mixing MOs

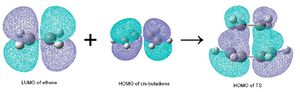
For a diels alder cycloaddition reaction to occur, the reacting orbitals must both be symmetric or antisymmetric. The MOs used to form the new bond are the HOMO and LUMO from cis-butadiene and ethene respectively as they are both antisymmetric.

To obtain the product of the reaction, an IRC using the same method as when optimising the boat and chair transition structures (50 points, one force calculation but in the reverse direction) was used and then a B3LYP optimisation to a minimum. The product obtained from the IRC was cyclohexene:

Published IRC optimisation using B3LYP: DOI:10042/to-1455

Pentahelicene

Cyclohexa-1,3-diene reaction with maleic anhydride

The method used to find the TS for the endo form was redundant coordinates and to find the TS for the exo form was QST2.

	Endo DOI:10042/to-1456	Exo DOI:10042/to-1457
jmol	Pentahelicene	Pentahelicene
Total Energy/HF	-612.6834	-612.67931
Av bond forming distance/Å	2.26858	2.29104
Av "through space" distance/Å	2.99035	3.02771

The total energy of the endo transition state is lower because the exo form is more strained. In the exo form, the O=C-O-C=O is opposite the bridging sp3 carbons whereas the O=C-O-C=O is opposite sp2 carbons in the endo form. Therefore in the exo form, the opposite carbons' hydrogens and O=C-O-C=O are closer in space to each other hence there are more unfavorable steric interactions.

	Endo	Exo
HOMO

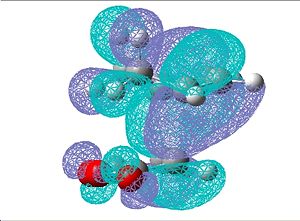
The two large lobes between the cyclohexa-1,3-diene and maleic anhydride fragments in the transition state proves that there is an interaction between the bond forming atoms. From the HOMOs of both endo and exo, there is no noticable secondary orbital interactions between the O=C-O-C=O fragment and the remainder of the system therefore the reason for the endo transition state being the kinetic product is only due to the endo form being less strained.

Another method to show that there is no secondary orbital interactions is to compare the partially formed bond lengths of the conformation. As the difference between the exo and endo transition states' bond forming distance is small, the calculation proves that there are no secondary orbital interactions between cyclohexa-1,3-diene reaction and maleic anhydride (because secondary orbital interactions are expected to reduce the bond forming distance greatly).

To obtain the endo and exo products, IRC's using the same method as when optimising the boat and chair transition structures was used and then a B3LYP optimisation to a minimum:

Endo DOI:10042/to-1550	Exo DOI:10042/to-1458
Pentahelicene	Pentahelicene

Conclusion

Any of the three methods to find transition states shown in the cope rearrangement tutorial can be used. However they each come with disadvantages; the common one being that if the guess TS structure is not close enough to the actual then the calculation fails. A useful feature of computing from transition states is the ability to produce a product or reactant structure using IRC.

An effect that was neglecting in my Diels Alder calculations was correlation effects. This is because the highest level method that I used, B3LYP/6-31G*, is incapable of taking correlation effects into consideration. A method that does is MP2.