Rep:Mod:ard16
Arun's Wiki Report
Ammonia (NH3)
Ammonia |
Optimisation Details
The optimisation file is linked to here
| Element | Method Used |
|---|---|
| Calculation Method | RB3LYP |
| Calculation Type | FREQ |
| Basis Set | 6-31G(d.p) |
| Final Energy | -56.55776873 (a.u) |
| RMS Gradient | 0.00000485 (a.u.) |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986274D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Structural Information
| Element | Detail |
|---|---|
| Point Group | C3v |
| Bond Distance (Angstroms) | 1.01798 |
| Bond Angle (degrees) | 105.741 |
Atomic Charges(by NBO)
Charge on N: -1.125
Charge on H : 0.375
This is expected as Nitrogen is more electronegative than Hydrogen so the bond is polarised, with the electrons density drawn more towards Nitrogen than the Hydrogens. As Nitrogen has a very high negativity this polarisation is significant, giving it a significantly negative atomic charge.
Vibrational Information
The Vibrational modes found are shown in the following figure:

Vibrational Analysis
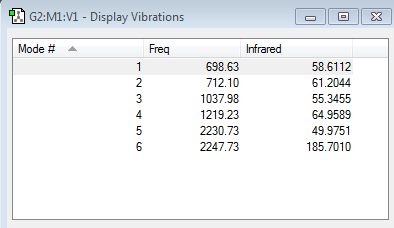
From the 3N-6 rule, 6 vibrational modes would be expected, and exactly 6 were found. Each frequency has a different intensity because their interactions with IR radiation differ. Interaction with IR depends on a change in dipole moment during the vibration: the first three modes have relatively large intenisties because they cause a significant change in dipole moment, whereas modes 4-6 have very low intensities because only a very small change in dipole moment occurs.
Two pairs of modes were degenerate, (mode pairs 2 and 3 at 1693.95cm-1, and mode pair 5 and 6 at 3589.82cm-1 respectively.) Modes 1,2 and 3 are bends, while 4, 5 and 6 are stretches. Bend 1 (1089.54 cm-1) is the umbrella mode. The vibrational mode 4, (3461.29cm-1) is the symmetric stretch. In an experimental spectrum of Gaseous ammonia I would expect to see 2 bands, as modes 4,5 and 6 have intensities which are very small, so would be deemed insignificant. Modes 2 and 3 are degenerate so only peaks corresponding to vibrational modes 1 and 2 at around 1694cm-1 and 1090 cm-1 would be seen. All four frequencies have been observed experimentally [1], thanks to the use of innovative technology, both Michelson interferometers and Fourier Transform Infrared (FTIR) spectrometers allowed a high resolution spectrum to be acquired, recording peaks at 1139 cm-1, 1757 cm-1, 3464 cm-1, and 3525 cm-1 respectively. The slight discrepencies between the frequencies can be explained by the limitations of the gaussian programme, perhaps not finding exact Molecular orbital structure which appears in nature.
Nitrogen (N2)
Nitrogen |
Optimisation Details
The optimisation file is linked to here
| Element | Method Used |
|---|---|
| Calculation Method | RB3LYP |
| Calculation Type | FREQ |
| Basis Set | 6-31G(d.p) |
| Final Energy | -109.52412868(a.u.) |
| RMS Gradient | 0.00000060 (a.u.) |
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400954D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Structural Information
| Element | Detail |
|---|---|
| Point Group | D∞H |
| Bond Distance(Angstroms) | 1.10550 |
| Bond Angle (degrees) | 180 |
Vibrational Information
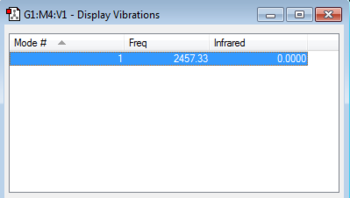
One Vibrational mode,a stretch, is found at 2457.33 cm-1. This is in corresponds with the 3N-5 rule for linear molecules. The intensity of the stretch is zero because as nitrogen is a homonuclear diatomic molecule, it has no dipole and no dipole is generated by the symmetric stretch. Therefore it does not interact with IR radiation so no peak would be expected to been seen in an IR spectrum.
Hydrogen (H2)
Hydrogen |
Optimisation Details
The optimisation file is linked to here
| Element | Method Used |
|---|---|
| Calculation Method | RB3LYP |
| Calculation Type | FREQ |
| Basis Set | 6-31G(d.p) |
| Final Energy | -1.17853936 (a.u) |
| RMS Gradient | 0.00000017 (a.u.) |
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Structural Information
| Element | Detail |
|---|---|
| Point Group | D∞H |
| Bond Distance(Angstroms) | 0.74279 |
| Bond Angle (degrees) | 180 |
Vibrational Information
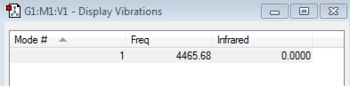
One vibrational mode, a stretch, was found at 4465.68 cm -1. As Hydrogen is a homonuclear diatomic molecule, like nitrogen there is no change in dipole moment during the vibration so it is not IR active. Therefore the intensity of the peak is zero, and would not be seen experimentally.
Haber-Bosch Process
The process by which ammonia is produced industrially. Ammonia is vital for agriculture as as a fertiliser, among a wide range of other uses including a popular solvent in the chemicals industry. In the process Nitrogen is added to Hydrogen to produce ammonia in the following equation:
N2 + 3H2 -> 2NH3
Using the energy gathered in the above optimisations I will calculate the energy change of reaction.
| Species | Energy (a.u.) |
|---|---|
| NH3 | -56.55776873 |
| 2*NH3 | -109.52412868 |
| N2 | -113.11553746 |
| H2 | -1.17853936 |
| 3*H2 | -3.53561808 |
Using the energy of both the reactants (3H2 + N2) and the products (2NH3) in the above table and using the formula Energy(products)-Energy(reactants)=Energy(reaction) below produces the energy of the reaction in a.u.
Energy of reaction = ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070 a.u.
This can be converted into the SI unit for energy of reaction to give:-146.48 Kj/mol. As the energy of reaction is negative, and so exothermic, the reaction is theorised to be favourable and so spontaneous. The enthalpy of reaction is determined as -91.55Kj/mol[2], which represents a significant difference from the computed result. The sign however is consistent. The large difference in magnitude could be down to the fact that the energy of reaction is recorded at 0K, whereas the standard enthalpy of reaction is recorded at 298K.
Silanone (H2SiO)
Hydrogen |
Silanone or oxosilane is equivalent to methanal however, with silicon as the central atom in place of carbon. Like the entire family of silanones (analgous to the ketones) it is very reactive, only very few silanones have been isolated or even detected and then only under specialised conditions. The reactivity of silanone can be seen from the Molecular Orbitals, particularly as the LUMO-HOMO gap is very small. The pi bond between silicon and oxygen is very weak as the 2p-3p orbital overlap is weak due to the large size of the 3p orbital, when compared to the 2p orbital and the difference in energy. This means that the central silicon favours an sp3 hybridisation as oppose to the sp2 present in silanone.
Optimisation Details
The optimisation file is linked here
| Element | Method Used |
|---|---|
| Calculation Method | RB3LYP |
| Calculation Type | FREQ |
| Basis Set | 6-31G(d.p) |
| Final Energy | -365.90001403 (a.u) |
| RMS Gradient | 0.00000941 (a.u.) |
Item Value Threshold Converged?
Maximum Force 0.000023 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Predicted change in Energy=-4.981719D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4865 -DE/DX = 0.0 !
! R2 R(1,3) 1.4865 -DE/DX = 0.0 !
! R3 R(1,4) 1.5317 -DE/DX = 0.0 !
! A1 A(2,1,3) 111.6859 -DE/DX = 0.0 !
! A2 A(2,1,4) 124.1571 -DE/DX = 0.0 !
! A3 A(3,1,4) 124.1571 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Structural Information
| Element | Detail |
|---|---|
| Point Group | C2V[3] |
| Si=O Bond Distance(Angstroms) | 1.53172 |
| Si-H Bond Distance(Angstroms) | 1.48652 |
| O-Si-H Bond Angle (degrees) | 124.157 |
| H-Si-H Bond Angle (degrees) | 111.686 |
Atomic Charges(by NBO)
Charge on Si: 1.472
Charge on O: -1.001
Charge on H : -0.236
This is expected as Oxygen is the most electronegative atom so will polarise the covalent bond with silicon drawing electron density toward the Oxygen. In the case of the Si-H bond, Hydrogen is slightly more electronegative so polarises the bond, but not to the same degree as with Oxygen. A combination of the polarisation of both these factors leads to the positive atomic charge value on silicon.
Vibrational Analysis
There are 6 Vibrational Modes, all are non-degenerate and all cause a change in dipole moment, so have reasonable intensities. I would therefore predict all six to be seen experimentally.In practise the experimental spectrum is very difficult to obtain due to the instability of silanone.
Molecular Orbitals
Fist examining the structure via VB (valence bond) theory. Both the central silicon and the neighbouring oxygen are sp2 hybridised. For silicon two of the sp2 orbitals form bonds with the hydrogens, and the remaining orbital overlaps with one of the sp2 orbitals from the oxygen. Oxygen's other two sp2 orbitals are filled by lone pairs. The pi bond is therefore formed by the 3p-2p overlap between oxygen and silicon. Due to the energy difference and size difference between the orbitals the bond formed is weak.
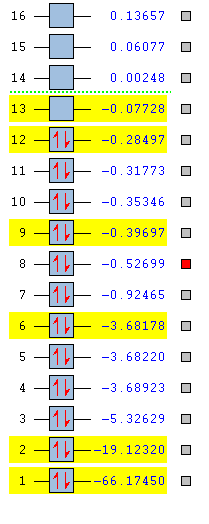
The energies of the MOs for silanone were calculated and I have selected a few for visualisation.
MO number 6, One of the 2p orbitals on the silicon, MOs 4 and 5, are also 2p orbitals for silicon in different orientations, hence have almost identical energies. These are very low energy core orbitals and do not interact in bonding.

MO number 8. This is an antibonding sigma orbital, originating from overlap between the silicon and oxygen sp2 orbitals. The nodal plane perpendicular to the internuclear axis is a clear indication of anti-bonding character.

MO number 11. This π bonding MO is made up of the overlap between the 2p and 3p orbitals of the oxygen and silicon respectively. It is the counterpart to MO 13, the anti-bonding orbital between these two MOs. The fact that the gap between MO 11 and this MO is only just over 0.2 a.u. suggests that the interaction between them is quite weak and there is a large energy gap between the corresponding AOs. This is further evidence of the pi bond being particularly weak in silanone.

This is the highest occupied molecular orbital. It is an anti-bonding π orbital orginating from the out-of-phase interactions between the oxygen 2p and silicon 3p bonds respectively.

This is the lowest unoccupied molecular orbital. It is another anti-bonding π orbital orginating from the out-of-phase interactions between the oxygen 2p and silicon 3p bonds respectively. It is the counterpart to MO 11, the bonding orbital between these two MOs. This LUMO is quite low in energy, -0.07728 a.u., only around -0.21 a.u. higher in energy than the HOMO. This means the molecule will likely be vunerable to attack from nucleophiles, hence explaining its high reactivity.
Methanal (H2CO) (Independent Section)
Methanal |
I willll compare particularly the Vibrational analysis of silanone with its corresponding carbon equivalent, methanal.
Optimisation Details
The optimisation file is linked here
| Element | Method Used |
|---|---|
| Calculation Method | RB3LYP |
| Calculation Type | FREQ |
| Basis Set | 6-31G(d.p) |
| Final Energy | -114.50319933 (a.u) |
| RMS Gradient | 0.00006910 (a.u.) |
Item Value Threshold Converged?
Maximum Force 0.000182 0.000450 YES
RMS Force 0.000080 0.000300 YES
Maximum Displacement 0.000231 0.001800 YES
RMS Displacement 0.000142 0.001200 YES
Predicted change in Energy=-3.380743D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1106 -DE/DX = -0.0001 !
! R2 R(1,3) 1.1106 -DE/DX = -0.0001 !
! R3 R(1,4) 1.2068 -DE/DX = -0.0002 !
! A1 A(2,1,3) 115.2203 -DE/DX = 0.0 !
! A2 A(2,1,4) 122.3899 -DE/DX = 0.0 !
! A3 A(3,1,4) 122.3899 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Structural Information
| Element | Detail |
|---|---|
| Point Group | C2V |
| C=O Bond Distance(Angstroms) | 1.20676 |
| C-H Bond Distance(Angstroms) | 1.11056 |
| O-C-H Bond Angle (degrees) | 122.390 |
| H-C-H Bond Angle (degrees) | 115.220 |
Vibrational Analysis
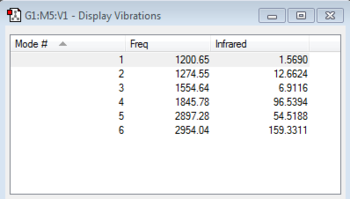

Just like silanone there are 6 vibrational Modes, however the frequencies and intensities of the modes differ significantly. All of the vibrational modes for methanal correspond to higher frequencies than their counterparts for silanone. This is expected as carbon is a lighter atom than silicon so its vibrations will be at a higher energy (v = (1/2*π*c)*(k/μ)-2. This is the key factor however the C=O bond is stronger than the Si=O bond, and this effect acts in the opposite direction, reducing the difference in vibrational frequencies. Silicon is less electronegative than carbon, so silanone has a greater dipole moment, so are likely to be more IR active, hence why most of the intenisties are larger for silanone than methanal.
References
- ↑ 1.0 1.1 J. Melville, Infrared Spectroscopy and Interferometry as Methods for Structural Determination of Ammonia, Physical Chemistry Laboratory, UC Berkeley College of Chemistry, 2014.
- ↑ 2.0 2.1 C.E. Vanderzee, D.L. King J. Chem. Thermodyn., 4 (1972), p. 675
- ↑ 3.0 3.1 Silanone point group literatur-eA comparison of the energies of double bonds of second-row elements with carbon and silicon Paul v. R. Schleyer and Daniel. Kost Journal of the American Chemical Society 1988 110 (7), 2105-2109 DOI: 10.1021/ja00215a016- .