Rep:Mod:aps315TS

Introduction

In a simplistic view, a transition state is classified as the highest energy point along a reaction coordinate. As a result, it is characterized as a stationary point and can be confirmed by determining the first derivative of the reaction coordinate as zero. However, this approximation is not an accurate representation of a chemical system undergoing a reaction. This constricted approximation does not account for the possibility of displacement from a system's equilibrium. A chemical system can in fact be displaced in 3N-6 degrees of freedom and a Potential Energy Surface (PES) is a more accurate description of a chemical system undergoing a reaction. A PES is a plot of potential energy against two combinations of these possible degrees of freedom. On a PES a transition state is now characterized as a saddle point and can be confirmed as having a first derivative equal to zero and a second derivative that is negative.

Nf710 (talk) 21:13, 21 March 2018 (UTC) The surface you are talking about it actually 3N-6. At a TS all the hessian eigen values are positive for all the 3n-6 dimensions apart from 1 which is negative and this is the reaction coord.

This report shall discuss the determination of transition states for three pericyclic reactions. These transition states will be located and characterized using GuassView by optimizing the reagents towards a minimum then subsequently optimizing the transition state using PM6 and B3LYP methods. The PM6 method is semi-empirical; it is effectively a less involved or reduced form of the Hartree-Fock method and is employed for swiftness. The B3LYP method was carried out using a 6-31G(d) basis set, it is a hybrid function utilizing he Hartree-Fock as well as the DFT method and is employed for a more accurate transition state determination.

Nf710 (talk) 21:13, 21 March 2018 (UTC) You could have gone into more detail here. Possibly added some equations.

In addition, Intrinsic Reaction Coordinate (IRC) calculations were utilized to examine the profile of the minimum energy pathway. An IRC follows the minimum energy pathway along the PES from the transition state towards the reactants and/or the products dependent upon how the calculation was ran. IRC calculations were employed to analyse the reaction profile, changes in bond length and to visualize the reaction.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Good job across this section. However, your butadiene is not optimised to a minimum, which led you to the wrong reactant MO energies.)

The reaction between butadiene and ethylene is a Diels-Alder reaction, a [4+2] cycloaddition, producing cyclohexene as the product. This pericyclic reaction proceeds via a concerted mechanism, with a single transition state.¹ In order for the reaction to occur butadiene must adopt the s-cis conformation. This reaction obeys normal electron demand with the diene (butadiene) being more electron rich than the dienophile (ethylene). A reaction scheme is presented below (Scheme 1).

**Scheme 1.** Reaction of Butadiene with Ethylene.

Molecular Orbitals

An MO diagram for the formation of the transition state between butadiene and ethylene was constructed using relative energies calculated in Gaussian for the transition state. This is presented below (Diagram 1). Butadiene's non-bonding molecular orbitals are not involved in the formation of the transition state and so have not been included to make the diagram clearer.

The MOs 16 and 19 produced by Guassian for the transition state are presented below and are correlated to the appropriate interactions in the MO diagram (Figure 1). These demonstrate orbital interactions between the HOMO of butadiene and the LUMO of ethylene, with both having asymmetric symmetry. As a result, it can be inferred that in order for orbital interaction to be favorable and result in overall stabilization of the molecule, the symmetries must be the same (e.g asymmetric and asymmetric) and they must have non-zero orbital overlap integrals. This arises due to the requirement for an overall symmetric function and non-zero overlap integrals corresponding to orbital spacial overlap.² A symmetric-symmetric and asymmetric-asymmetric interaction will have a non-zero overlap while opposing symmetries (asymmetric-symmetric/ symmetric-asymmetric) will have zero overlap integral and an overall asymmetric function.

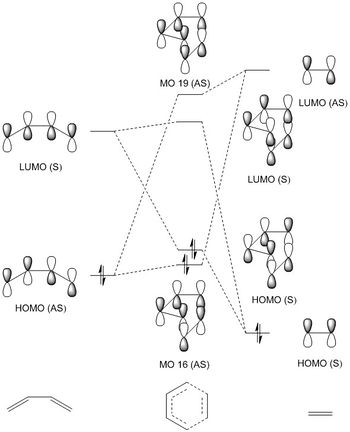
Figure 1.

Ethylene

Ethylene HOMO

Ethylene LUMO

Butadiene

Butadiene HOMO

Butadiene LUMO

Transition State

TS MO 16 (HOMO-1)

TS HOMO

TS LUMO

TS 19 (LUMO+1)

Carbon Bond Lengths

The Diels-Alder reaction involves the formation of two C-C sigma bonds and the breaking of three C-C pi bonds. The C-C bond lengths calculated by Guassian for the reagents, transition state and product are presented below (Table 1). C-C bonds 1,2 and 6 correspond to the bonds of butadiene and bond 4 corresponds to the bond of ethylene (Diagram 2).

Typical bond lengths for C-C sp² single and double bond as well as sp³ single bond are 1.460, 1.316 and 1.507 Å respectively. The values obtained vary by approximately 0.01 Å compared with typical values, however, when compared with literature values for cyclohexene, the values compare well with slight deviation.³ The double bond calculated is 0.012 Å longer than that in literature, this deviation most likely arises due to the method applied, PM6, providing less accurate values. The use of B3LYP/6-31G(d) would most likely provide a substantially closer value.

The typical van der Waals radius of a carbon atom is 1.70 Å whilst the length of the partly formed C-C bonds in the transition state are 2.113 and 2.116 Å. The van der Waals radius is defined as half the distance of closest approach between two non-bonded atoms, therefore the total distance is 3.40 Å. The values obtained are substantially shorter than this radius by 1.287 and 1.284 Å, aligning with the partial formation of C-C bonds in the transition state.

As the reaction progresses bonds 3 and 5 shorten as the C-C bonds are formed. Simultaneously, bonds 2,4 and 6 all elongate whilst bond 1 shortens, represented below in Graph 1.

**Table 1.** C-C Bond Lengths during Diels-Alder Reaction
Bond	Reagents Bond Length / Å	Transition State Bond Length / Å	Product Bond Length / Å
Bond 1	1.468	1.411	1.338
Bond 2	1.335	1.380	1.500
Bond 3	-	2.113	1.540
Bond 4	1.327	1.382	1.541
Bond 5	-	2.116	1.540
Bond 6	1.335	1.380	1.500

**Graph 1.** C-C Bond Length Changes with Reaction Coordinate.

Bond Vibration

The vibration that corresponds to the formation of the transition state is presented below (Image 2). The formation of the new sigma bonds can be seen to occur simultaneously, this demonstrates the synchronous, concerted nature of the Diels-Alder mechanism.

Relevant Files

Butadiene - File:BUTENE_OPT(1)_APS315.LOG

Ethylene - File:ETHENE_OPT(1)_APS315.LOG

Transition State - File:EX1_TS_APS315.LOG

Cyclohexene - File:PRODUCT_aps315.LOG

Transition State IRC - File:TS_IRC_aps315.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

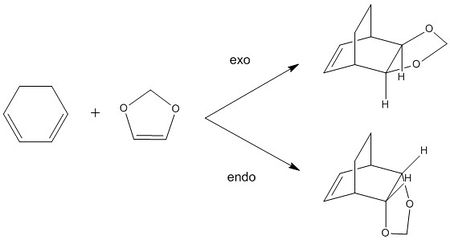
The reaction between cyclohexadiene and 1,3-dioxole is a Diels-Alder reaction, a [4+2] cycloaddition, producing two possible products dependent upon the orientation of molecule approach (Scheme 2). An exo product is formed when the substituents of the 1,3-dioxole are facing away from the cyclohexadiene π system. Alternatively, the endo product is formed when the substituents of the 1,3-dioxole are facing towards the cyclohexadiene π system. In general, the endo product is frequently the thermodynamically preferred due to secondary orbital effects that involve stabilizing overlap in the endo transition state. This pericyclic reaction proceeds via a concerted mechanism, with a single transition state.¹

Molecular Orbitals

An MO diagram for the formation of the transition state between cyclohexadiene and 1,3-dioxole was constructed using average relative energies calculated in Gaussian for the transition state. This is presented below (Diagram 2). Non-bonding molecular orbitals are not involved in the formation of the transition state and so have not been included to make the diagram clearer.

Due to the electron-donating nature of the oxygen atoms present in 1,3-dioxole, the dienophile becomes more electron rich, raising the energies of its HOMO and LUMO. This results in a [4+2] cycloaddition that obeys inverse electron demand.¹ When comparing the exo and endo transition states, both still obey inverse electron demand and follow the MO diagram displayed below, however, the relative energies of the molecular orbitals is shifted. The endo transition state can be seen to have a lower energy HOMO by 0.00492 Hartrees/particle and a higher energy LUMO by 0.00237 Hartrees/particle. This shift in energies arises due to stabilization of the endo HOMO by secondary orbital effects; overlap between the π system of cyclohexadiene and 1,3-dioxole. The exo transition state is only stabilized through primary interactions, whereas the endo transition state is stabilized through both primary and secondary interactions. This is presented below (Figure 2).

Nf710 (talk) 21:17, 21 March 2018 (UTC) You have just stated that the reaction is inverse and you have not investigated it quantitatively, by comparing reactant orbital energies on the same PES.

The associated MOs are presented below for both the Exo and Endo transition states (Figure 3). (Fv611 (talk) You optimised both TS correctly, but you have not placed the MOs in their correct order so this might come from an incorrect optimisation of your reactants. Your discussion of relative energies should also have been formulated in terms of energy gaps rather than absolute numbers.)

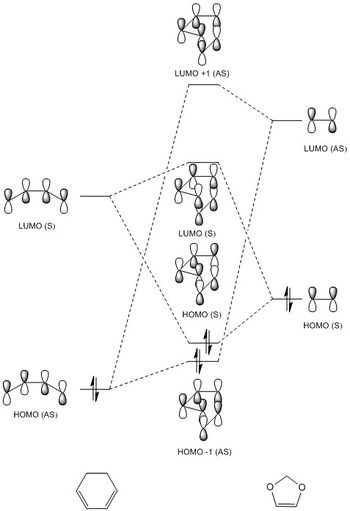
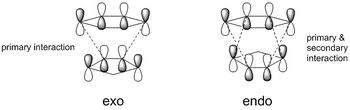
Figure 3.

Nf710 (talk) 21:19, 21 March 2018 (UTC) This is not correct, furthermore this diagram is quite difficult to understand. you should have drawn it at an angle.

Endo Transition State

TS MO 40 (HOMO-1)

TS MO 41 (HOMO)

TS MO 42 (LUMO)

TS MO 43 (LUMO+1)

Exo Transition State

TS MO 40 (HOMO-1)

TS MO 41 (HOMO)

TS MO 42 (LUMO)

TS MO 43 (LUMO+1)

Thermochemistry

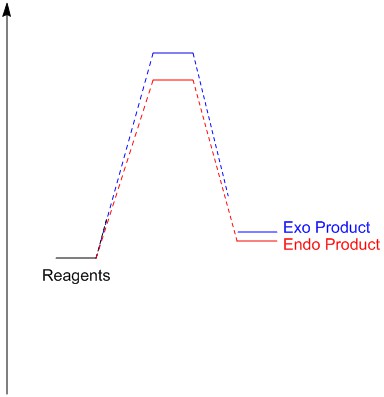
The energy barriers and the reaction energies at room temperature are presented below (Table 2)(Figure 4). The energy barrier is the activation energy required for a reaction to occur, a product with a lower activation energy is kinetically preferred as it will more readily overcome the energy requirement for the reaction and thus form faster. The endo product can be seen to have a lower activation energy and thus can be determined to be the kinetically preferred product. This arises due to the endo transition state being lower in energy as it is stabilized by secondary orbital effects (Figure 2).

The reaction energy is characterized as the difference in energy between the reactants and products. The product with the more negative reaction energy is thermodynamically preferred as it is the more stable. The endo product can be seen to have a more negative reaction energy and thus can be determined to be the thermodynamically preferred product. This most likely arises due to steric clash that can be observed in the exo product between the carbon bridge and five-membered ring which is not observed for the endo product.

**Table 2.**Activation and Reaction Energies
Product	Activation Energy / Hartrees/particle	Activation Energy / kJ/mol	Reaction Energy / Hartrees/particle	Reaction Energy / kJ/mol
Endo	0.057016	149.695519	-0.030848	-80.99143017
Exo	0.060002	157.535263	-0.028146	-73.89732863

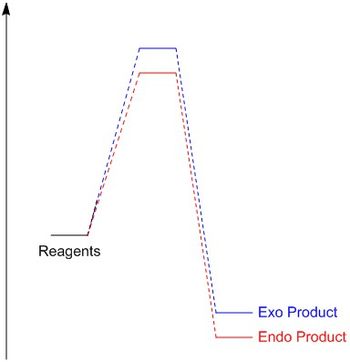
Nf710 (talk) 21:22, 21 March 2018 (UTC) Your energies are slightly out. I suspect that your reactant energies have been slightly miss calculated. However you have still come to the correct conclusions. There were points where you could have gone into more detail.

Relevant Files

Cyclohexadiene(BL3YP) - File:CYCLOHEXADIENE(2)_aps315.LOG

1,3-Dioxole(B3LYP) - File:DIOXOLE(2)_APS315.LOG

Endo Product(B3LYP) - File:ENDOPROD_APS315.LOG

Exo Product(BL3YP) - File:EXOPROD(2)_APS315.LOG

Exo TS (BL3YP) - File:EXO_TS(3)_aps315.LOG

Endo TS (BL3YP) - File:ENDO_TS(7)_aps315.LOG

Exercise 3: Diels-Alder vs Cheletropic

The reaction between xylylene and sulfur dioxide can proceed via two possible reaction mechanisms; a Diels-Alder reaction, a [4+2] cycloaddition, or a cheletropic reaction (Scheme 2). The Diels-Alder reaction can again proceed via endo or exo mechanisms dependent upon the orientation of approach of sulfur dioxide. The cheletropic reaction generates a five-membered heterocyclic ring product. Due to the significantly different mechanisms, as expected, the reaction profiles of these reactions vary greatly.

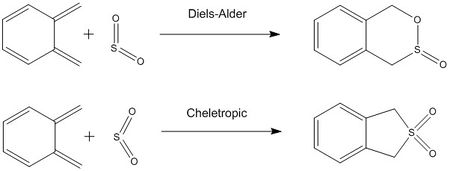
IRC

The IRC calculations performed for these three alternative mechanisms have been visualised and are presented below. The endo and exo Diels-Alder reactions can be seen to be asynchronous whereas the cheletropic reaction can be seen to be synchronous. Xylylene's lack of stability is displayed through the IRCs for the reactions; the bond lengths of the six-membered ring undergo variations throughout the IRC and equalize upon the formation of the product.

Endo Diels-Alder

Exo Diels-Alder

Cheletropic

Thermochemistry

The energy barriers and the reaction energies at room temperature are presented below (Table 3)(Figure 5). The data collected suggests that the endo Diels-Alder product is kinetically preferred with the mechanism having the lowest activation energy. This result arises due to reasons discussed for the previous example; secondary orbital interactions stabilise the endo product's transition state. However, the endo product can be seen to be at a higher energy than that of the exo product; this arises due to the destabilizing steric clash between the oxygen atom and the six-membered heterocyclic ring. The reaction energies of the three mechanisms are all substantially large, this arises due to the stability of the aromatic ring formed that provides a strong driving force to the products. The cheletropic product has a substantially higher activation energy than the Diels-Alder, however has the lowest energy product and thus is the thermodynamically preferred product. This result can be explained by examining bond energies; C-S 272 kj/mol, C-O 358 kj/mol and S=O 522 kj/mol. The S=O is markedly more stable than the alternative C-O and S-O bonds formed during the Diels-Alder reaction, making the cheletropic product more stable.

**Table 3.**Activation and Reaction Energies
Product	Activation Energy / Hartrees/particle	Activation Energy / kJ/mol	Reaction Energy / Hartrees/particle	Reaction Energy / kJ/mol
Endo	0.031064	81.55853821	-0.037798	-99.23865656
Exo	0.032581	85.541422	-0.038043	-99.88190411
Cheletropic	0.039566	103.880541	-0.059492	-156.1962579

(You're using far too many decimal places - 10 micro J/mol in the reactants! Tam10 (talk) 11:14, 16 March 2018 (UTC))

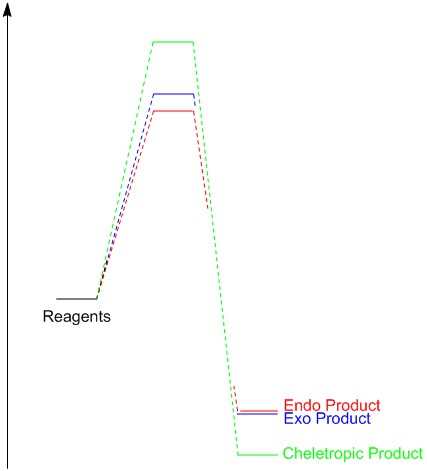
**Figure 5.** Reaction Profile of Xylylene and Sulfur Dioxide.

(Label the energy axis. If you put values on the profile it will make it easier to read the data Tam10 (talk) 11:14, 16 March 2018 (UTC))

Xylylene has an additional site where a Diels-Alder reaction can occur. This reaction is 'endocyclic', occuring with the diene present in the six-membered ring, the 'exocyclic' reaction was previously analysed. The energy barriers and the reaction energies at room temperature for these reactions are presented below (Table 4)(Figure 6). As can be seen, the product energies for both the endo and exo reaction are higher than the energies of the reagents. In addition, the activation energies are substantially higher than for the 'exocyclic' reaction. These results arise due to the lack of aromatic stability provided by the 'endocyclic' products.

**Table 4.**Activation and Reaction Energies for 'Endocyclic' Reaction
Product	Activation Energy / Hartrees/particle	Activation Energy / kJ/mol	Reaction Energy / Hartrees/particle	Reaction Energy / kJ/mol
Endo	0.042574	111.778046	0.006113	16.0496827
Exo	0.045558	119.612538	0.00781	20.505157

**Figure 6.** Reaction Profile of 'Endocyclic' Xylylene and Sulfur Dioxide.

Relevant Files

'Exocyclic' Diels-Alder

Xylylene - File:XYLYLENE_APS315.LOG

Sulfur Dioxide - File:SO2_APS315.LOG

Endo TS - File:EX3_ENDO_TS(8)_APS315.LOG

Endo IRC - File:EX3_ENDO_IRC(1)_APS315.LOG

Endo Product - File:EX3_ENDOPROD_APS315.LOG

Exo TS - File:EX3_Exo_TS(1)_APS315.LOG

Exo IRC - File:EX3_EXO_IRC_APS315.LOG

Exo Product - File:EX3_EXOPPROD(1)_APS315.LOG

Cheletropic

Cheletropic TS - File:EX3_CHELE_TS(2)_APS315.LOG

Cheletropic IRC - File:EX3_CHELE_IRC(1)_APS315.LOG

Cheletropic Product - File:EX3_CHELE_PROD_APS315.LOG

'Endocyclic' Diels-Alder

Endo TS - File:EX3(1)_ENDO_TS_APS315.LOG

Endo Product - File:EX3(1)_ENDOPRODUCT_APS315.LOG

Exo TS - File:EXO(1)_Exo_TS(1)_APS315.LOG

Exo Product - File:EX3(1)_EXOPRODUCT_APS315.LOG

Conclusion

The data produced by GuassView correlates well with pre-existing theory. For instance, the effects of the endo rule, aromatic stability and steric clash could all be employed to explain and align with the results obtained. The computational methods employed proved highly effective with limited knowledge of the reactions required. Only a fundamental understanding of chemistry is required to conduct and analyse these methods.

The approach of modelling provides unparalleled access to understanding chemical reactions and pathways and allows for chemistry to be conducted theoretically with well estimated outcomes that align with experimental values.

References

1. J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, 2, 2012.

2. P. Atkins, J. Rourke, T. Overton and F. Armstrong, Shriver & Atkins Inorganic Chemistry, Oxford University Press, 5, 2010.

3. A. Orpen and D. Watson, J. Chem. Soc. Dalt. Trans., 1987.