Investigations into the Cope Rearrangement

Stabilising the Reactant

Introduction

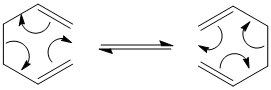
The cope rearrangement is an intramolecular pericyclic reaction, which is known to proceed via a chair-like transition state. The reactant is 1,5-Hexadiene, this molecule exists in a variety of conformers. These were constructed using Gaussview, and optimised with Gaussian. The procedure and results are described below.

Anti-hexadiene

hexadiene_anti

Procedure

The C2-C5 torsion angle was set to 180°, and the optimisation run with Hartree-Fock method and 3-21G basis set. The log file was checked to confirm RMS force had converged. The energy was read from the summary file. The molecule was "symmetrised" using Gausview with 0.01 tolerance constrained to the sub group C1.

Results

Energy: -231.68540 Hartrees = -608,290 kj.mol-1

Point group: C_2h

Gauche-hexadiene

hexadiene_anti

Procedure

The molecule was rotated and torsion angle between C2-C5 about the central C-C axis was set to 60°. This molecule was optimised using the same level of theory as before. During optimisation the C2-C5 torsion angle increased from 60° to 64.2°. This still lay within the gauche conformation (30°-90°). Optimisation was again confirmed by seeing that both force and displacement had converged in the log file.

The molecule no has greatly reduced symmetry, the tolerance for the point group was increased to 0.5, but no higher symmetry could be found other than a C₂ rotational axis.

Results

Energy: -231.69167 Hartrees = -608,307 kj.mol-1

This equates to a predicted 17kj.mol^-1 extra stability for the gauche conformation over that of the anti.

Point Group: C₂

Prediction of lowest energy conformation of hexadiene

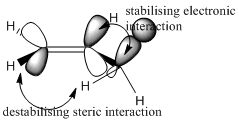
We have seen the gauche confomation about the C3-C4 axis gave rise to a more thermodynamically stable product. The reason for this is predicted as being the A^1,3-eclipsed conformation that arises in both alkene bonds. This involves a stabilising interaction between the C=C π* and the C-C σ bond, which compensates for the additional repulsion experienced by the now eclipsed protons.

This is described pictorially below:

Being gauche about the C3-C4 axis gives rise to 3 main conformations to be investigated, there would in fact be more than this but the high symmetry of the molecule reduces the number.The molecules are shown below, from the perspective of looking through the C3-C4 axis (Gauche a-c, from left to right).

One would expect the conformation that has the C=C bonds arranged furthest from each other in space, gauche c shown above, will result in the lowest energy conformer, because it minimises internal steric repulsions within the molecule. The calculated energies from Gaussian contradict this.

*Energies of Different Gauche Conformations*
Name	Torsion angle*	Energy / Hartrees	Energy / kjmol^-1
Gauche a	13°	-231.69167	-608,307
Gauche b	67°	-231.69266	-608,309
Gauche c	119°	-231.69153	-608,306

* torsion angle between terminal carbons relative to central C3-C4 bond

In order to explain this one needs to adopt a molecular orbital approach described below are the MOs of the three conformations (Gauche a-c, from left to right).

We can see that the whilst Gauche a and Gauche b contain an interaction between the alkene bonds, Gauche c does not. This interaction is predicted as being stabilising. The reason for the greatest thermodynamic stability of the Gauche b conformation is therefore rationalised as being the conformation that has minimised the internal steric repulsions, whilst at the same time maintaining the interaction between the alkene bonds.

All conformations are in good agreement with the data¹.

Optimisation of Anti-hexadiene conformer

The "anti-hexadiene b" conformation was obtained by setting the torsion angle of the terminal carbons relative to the C3-C4 axis to 180°. The molecule was initially optimised with the Hartree-Fock method and the 3-21G basis set.

The inital optimisation gave an energy of -231.69254 Hartrees which is equivalent to -608309 kjmol^-1. This therefore is a very low energy conformation (relative to previous calculations), being only 0.00012 Hartrees higher in energy than Gauche b.

The reason for this is predicted as the following. Both alkenes have adopted the A^1,3-eclipsed conformation which provides hyperconjugation between the C=C π* and the C-C σ bonds as previously described. The molecule has also adopted a relatively linear shape, minimising steric repulsions. However there is no opportunity for the two alkene bonds to have steroelectronic interactions, therefore this anti-conformation is of slightly higher energy than gauche b.

The point group of this species is determined as C_i indicating the centre of inversion that exists about the mid-point of the C3-C4 bond.

An optimisation is then carried out using density functional theory. The method used is B3LYP and the basis set is 6-31G*. The energy obtained is -234.61170 Hartrees, this is equivalent to -615973 kjmol^-1. This figure is not comparable to the previous optimisation as it is calculated with a different basis set.

Again both of these values for electronic energy are identical to the data¹.

Vibrational Analysis of Anti-hexadiene conformer

A Vibrational analysis was carried out using B3LYP/6-31G*. The spectrum is displayed below.

The gradient of the potential energy surface finds the negative force: F=-dV/dx

Together with Hooke's law: F=-kx therefore: k=d²V/dx²

A minimum occurs when the second derivative is positive, this means that k will also be positive. The frequency of a diatomic is related to the bond strength as shown below:

f = (k/ų)^1/2 with f as the frequency, k as bond strength and μ as reduced mass of the diatomic molecule

A positive value for all frequencies correlates to positive k values. Therefore, the fact that there are no negative frequencies implies that we have reached a minimum in energy.

Stretching frequencies for anti-hexadiene conformer
stretching mode	frequency/cm^-1
C3-C4	1034
C2-C3 and C4-C5 in phase	1203
C2-C3 and C4-C5 out of phase	1251
alkenes in phase	1731
alkenes out of phase	1734
C-H stretch	3022
C-H stretch	3031
C-H stretch	3060
C-H stretch	3080
C-H stretch	3135
C-H stretch	3137
C-H stretch	3155
C-H stretch	3156
C-H stretch	3234
C-H stretch	3234
C-H stretch	3155

Of particular interest are the absorption frequencies of the two alkene bonds, they form at 1731 and 1734 cm^-1. The stretching vibrations associated with these frequencies are shown below, with the two 1731 stretches on the left and the two 1734 stretches on the right.

Because the stretching frequency at 1731cm^-1 is not associated with a changing dipole moment, it does not have the ability to interact with the infra-red radiation, therefore the intensity of this absorption is zero. This is not the case for the stretching mode at 1734cm^-1.

Thermochemistry of Anti-hexadiene conformer

The log file was examined to determine the thermochemistry of the molecule.

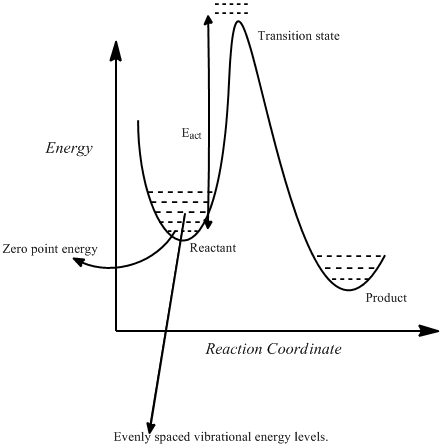
Zero-point correction

Because the molecules function as quantum harmonic oscillators one must take into account the vibrational energy levels. These have the following form:

E_vib = (v+1/2)ћω with v = 0,1,2,3, ...

The lowest vibrational energy of an oscillator is 1/2 ћω, this is known as the zero point energy. This must be taken into account when determining the energy differences between ground states and transition states, as described below. The zero point energy is part of the energy correction applied to the molecule during vibrational analysis.

The calculated zero point energy at 0K was 0.14249 Hartrees, applied to the original electronic energy this yielded an energy of -234.46921 Hartrees.

Thermal correction to energy

A further 0.00736 Hartrees was added to the total energy in order to account for the vibrational, rotational and translation energies at 298.15K and 1 atm.

Thermal correction to enthalpy

This is an additional correction applied to account for the thermal energy.

RT = 2.47882 kJmol^-1 = 0.00094 Hartrees

Thermal correction to Gibbs Free Energy

The final correction takes into account the entropy of the system. This involves a correction of -0.03991 Hartrees which is equivalent to -104.78371 kJmol^-1.

-TΔS = -104.78371 kJmol^-1 (T=298.15K)

Therefore the entropy, ΔS, is predicted to be 0.35145 kJmol^-1K^-1

All of these corrections were applied to the original energy of -234.61170 Hartrees to yield the final corrected energy of -234.50082 Hartrees.

Stabilising the Transtition State

Optimising the chair transition state

Two distinct methods exist for the optimisation of the chair conformation of the transition state. The first is the Berny optimisation, this is an expensive process in terms of calculation power it involves direct calculation of the transition state. The second, slightly more subtle method is a two step process, the first step involves fixing the half-bonds and allowing the two allyl fragments to optimise, the so called frozen coordinate optimisation (FCO). The second step then allows the half-bonds to transverse the potential energy surface until a minimum is reached (the rest of the species having already been optimised), this will be described as Hessian coordinate optimisation (HCO). This second method is much quicker to run in terms of calculation time as no force constants have to be calculated, however it requires that we already have an approximate guess for the half bond lengths. The two methods are described qualititively below in the form of a 2D Potential energy surface (PES).

Berny optimisation

An allyl fragment was optimised using the Hartree-Fock method with a 3-21G basis set and a a memory limit of 250mb. THe resulting structure had an energy of -115.82304 Hartrees and a C2v point group.

Two allyl fragments were then arranged in a chair-like transition state structure so that the terminal carbons on each fragment were approx. 2.2A from each other. And an optimisation and frequency analysis was run on this using the Berny transition state optimisation+frequency, with HF/3-21G and set to calculate force constants once.

Initially it was found from the log file that the transition state had not fully optimised with only the maximum displacement not having converged and the distances between the terminal carbons different in the fourth decimal place. Therefore the calculation was repeated on the now more optimised form, allowing Gaussian more time to refine its results. After this the structure was fully optimised with 2.02043A distance between the terminal carbons on both ends of the species.

The energy was recorded as -231.61932 Hartrees with a C2h point group. The structure is displayed below, with half bonds drawn using Gaussview as a visual aid.

With vibrational analysis there was found to be an imaginary frequency of magnitude 818 cm-1 this corresponded to a asynchronous contraction and expansion of the transition state half-bonds as shown below.

The MO approach shows no electron density between the terminal carbons within the HOMO, but there clearly contained within the LUMO. This reflects the need for electronic excitation in order to carry out this pericyclic reaction. Suprafacial components involved in the mechanism with 4n+2 (6) electrons therefore,Huckel's rules state thermal excitation is needed. The HOMO and LUMO are shown below, left and right respectively.

Frozen and Hessian Coordinate Optimisation

Using the redundant coordinate editor the two half-bonds were frozen at a distance of 2.02043A. The species was then optimised to a minimum using HF/3-21G. The half-bonds were then set to derivative using the coord. editor, and a minimisation carried out using a normal Hessian guess instead of calculating force constants (much less computing power needed).

It was found that the bond distance for half bonds was still correct to the previous calculation within 2 decimal places, i.e.2.02A. If a greater degree of accuracy was required a tight optimisation could be run, which has much smaller thresholds of convergence.

The reason for the lack of change percieved in half-bond length during the Frozen and Hessian coordinate optimisation was because the initial guess was so accurate. Ultimately both this method and Berny optimisation will arrive at the same results, they just take a different route (see PES above).

Optimising the boat transition state

The anti-Ci conformer described previously was copied twice into gaussview to create a multiple geometry. The first geometry was named the reactant molecule and the second geometry was named the product. The geometry was manipulated by setting the central dihedral angle to 0° and the C2-C3-C4 and C3-C4-C5 bond angles to 100° for both molecules, this ensured that they had the correct geometry to interconvert. They were labelled as shown below, ensuring they converted correctly.

The opt+freq job was submitted to Gaussian with a QST2 optimisation and HF/3-21G. This method works by working out the transition state on the basis that it must lie somewhere between the reactant and product in terms of geometric form. If the transition state is very different in structure to either reactant or product then the QST2 optimisation will not be an appropriate optimisation to carry out. The calculated transition state is displayed. It has one imaginary frequency of magnitude 840cm^-1 corresponding to an asymmetric stretching of the half-bonds.

Intrinsic Reaction Coordinate (IRC) Method

This method starts with the Transition state of a reaction, it then follows the energy pathway with the steepest gradient, leading to a minimum in the potential energy surface. This allows us to predict which confomer the product adopts, and in the case of the cope rearrangement this will also tell us the reactant form as well.

The job type was selected as IRC, with the guess method set as default and no solvation. The force constants were set to calculate once, the number of steps selected was 100 and the stepsize was set as 5 (irc=stepsize=5 in keywords). The method and basis set employed was HF/3-21G.

The calculation took approx. 1 hour to run on the laptop and terminated after 71 steps. The reaction pathway displayed as a function of energy is shown below.

Because the calculation terminated prematurely, an additional optimisation was required. The reaction pathway showed that an energetic minimum was very close to being reached, therefore only a low level of theory was used for optimisation. The conformation shown in the 71st step is optimised to a minimum using HF/3-21G, the conformation produced was the same in the structure and energy (-231.69167 Hartrees) as the "gauche a" conformation. This is consistent with the fact that the HOMO, which is known to largely determine the character of the molecule, has fully interacting alkene bonds, showing that it has the correct stereoelectronics to interact suprafacially as is required. Additionally it has a bent conformation indicating that its ready to undergo the intramolecular cope rearrangement.

Determination of Activation Energies

Both the hexadiene and the "gauche a" conformation and the boat and chair transition states were optimised using a high level of theory, B3LYP/6-31G*. The results are displayed below, and relate to the energies at 0k.

*Energies of conformations at 0K*
Conformation	Energy/Hartrees	Energy/kcalmol^-1
gauche a	-234.61069	-147,220.32
boat TS	-234.54309	-147,177.90
chair TS	-234.55693	-147,186.58

From this the activation energies were calculated and compared to the experimental values at 0k (Results Table 2)¹.


	Theoretical/kcalmol^-1	Experimental/kcalmol^-1
ΔE boat	42.42	44.7 +/- 2.0
ΔE chair	33.74	33.5 +/- 0.5

The calculated values are in excellent agreement with the experimental data. This indicates that the IRC method and subsequent optimisation, has located the correct conformation for the reactant.

Investigations into the Diels Alder Reaction

Basic Diels Alder

The classic diels alder reaction scheme is described below.

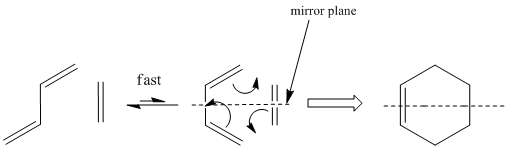
Whilst the trans conformation is thermodynamically more stable, it rapidly interconverts to the cis form at room temperature, as the barrier for rotation is reasonably low. Therefore the pericyclic mechanism is able to proceed. This is a good method of creating cyclohexene, which is a useful reagent for organic syntheses. The reaction is essentially irreversible due to the stable 6-membered ring configuration of the product.

Formally the reaction is described as a [4s + 2s] cycloaddition.

Optimising Reactants

Cis-butadiene was optimised using the semi-empirical AM1 method. The HOMO and LUMO were visualised using gaussview and are displayed below, left and right respectively.

if we imagine a plane of symmetry through the centre of the molecule (perpindicular to the C2-C3 bond axis, and bisecting it), we can clearly see that the HOMO is asymmetric about this plane whereas the LUMO is symmetric.

Clearly if we were to draw a mirror plane through ethylene the HOMO, pi orbital, would be symmetric, and the LUMO, pi* orbital, would be asymmetric about this plane. In order to interact MOs must have the same symmetry, therefore we clearly have a HOMO-LUMO interaction.

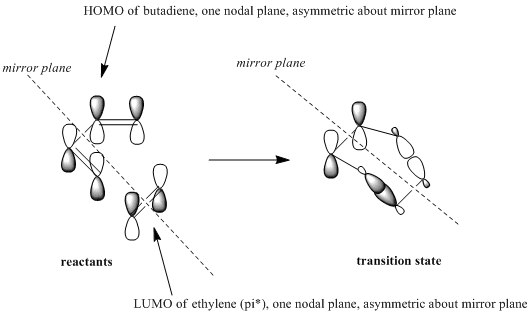
Optimising Transition State and Frequency Analysis

The transition state was drawn by converting the terminal carbons on the cis-butadiene into a sp³ hybridisation state, these were then linked to the ends of ethylene via a half bond, the carbons on the ethylene were also set to adopt an sp³ hybridisation state. All bonds except the TS half-bonds were then converted into "1.5 bonds" with bond distances set at 1.45A (halfway between double, 1.35A, and single, 1.54A). The half-bond distances were set as 2.02A, this figure was chosen as it this was the previously calculated half-bond length for the cope rearrangement. This example is assumed to be analgous as again there are no heteroatoms involved. Because we are able to supply a lot of information to Gaussian in terms of accurate initial guesses, the Berny method of optimisation was chosen. With the accurate initial guess predicted to negate the large amount of calculation time needed for a Berny optimisation.

An optimisation and frequency analysis was run, optimising to a TS Berny with the semi-empirical AM1 method, no solvation, default guess mode, opt=noeigen entered into the key words (to prevent Gaussian from crashing if more than one imaginary frequency is located) and the force constants set to calculate just once.

BasicDA_TS

The geometry of the TS is shown above, the half-bond lengths were calculated to be 2.12A.

The results indicated that a transition state had been found with the log file showing a stationary point had been reached well within the thresholds for convergence:


	Value	Threshold	Converged?
Maximum Force	0.000022	0.000450	YES
RMS Force	0.000004	0.000300	YES
Maximum Displacement	0.000566	0.001800	YES
RMS Displacement	0.000139	0.001200	YES

Furthermore this stationary point was confirmed as a maximum by noting that the frequency analysis recorded an imaginary frequency of magnitude 956cm^-1. This frequency relates to the synchronous stretch of the two half-bonds. The lowest positive frequency was at 147cm^-1 and corresponded to a bending motion.

The reason why an imaginary frequency relates to a Transition State, i.e a maximum in the Potential energy is as follows. As has already been described the second derivative of the potential energy surface is equal to k, a maxima will give a negative second derivative, and therefore a negative k.

Because the of the following relationship: f = (k/u)^1/2 with f as the frequency, k as bond strength and µ as reduced mass of the diatomic molecule

A negative k will give some multiple of (-1)^1/2 i.e. an imaginary frequency.

Molecular Orbital Intepretation of Transition State

Usually the HOMO is the most relevant orbital in determining the character of a molecular species. The HOMO, shown to the right, demonstrates significant shared electron density along the TS half-bonds. The HOMO at the transition state is asymmtetric about the central mirror plane.

From the earlier LCAO diagram it can be seen that both the reactants are asymmetric about the central mirror plane. And the HOMO shows that the transition state is asymmetric about this same plane.

There are 6 (4n+2) π electrons in the aromatic system of the transition state. The mechanism proceeds with suprafacial geometry therefore Huckel's rules state that the reaction will proceed thermally.

The reaction is allowed because both reactants have the same MO symmetry, therefore their orbitals can interact.

Determining Activation Energy

An optimisation was carried out on the reactants and products using the B3LYP method and the 6-31G* basis set.

Energy of Reactants = -155.98595 Hartrees (diene) + -78.58746 Hartrees (dienophile)

Energy of Transition state = -234.54390 Hartrees

Energy Difference = 0.02951 Hartrees = 18.52 kcalmol^-1 = 77.49 kJmol^-1

Clearly this energy is very much in excess of RT (approx.=2.5kJmol-1). Therefore this reaction will proceed very slowly under standard conditions, requiring a high temperature to obtain a good yield.

Advanced Diels Alder Reaction

The reaction between cyclohexa-1,3-diene and maleic anhydride can go via one of two transitions states through a cycloaddition mechanism.

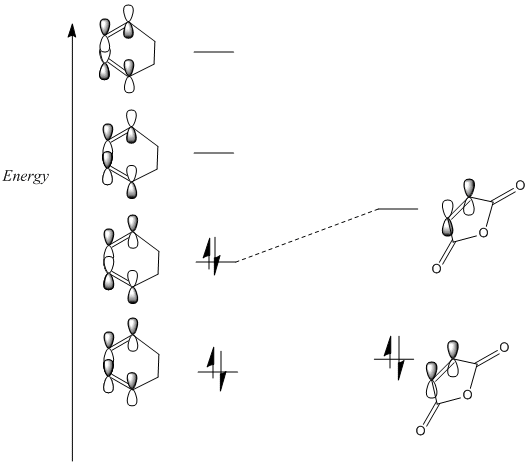
The electronegativity and conjugation of the maleic anhydride lowers its energy relative to that of an alkene. This provides better interaction between the HOMO of the diene and the LUMO of the dienophile because they are closer in energy. This is demonstrated below in an MO diagram. This improved orbital interaction should lead to a lower energy transition state and therefore a faster reaction.

The transition states were guessed using the same approximations for bond/half-bond lengths as the previous Diels Alder transition state. An opt. and freq. analysis were carried out on both the exo and the endo TS using a Berny TS calculating force constants once, with the AM1 semi empirical method.

Once the optimisation was complete, the transition states were confirmed by visualising the vibrations, there was an imaginary frequency corresponding to a synchronous stretching of the TS half bonds for both the endo and exo conformations. The endo and exo vibrations were of magnitudes 757cm^-1 and 812cm^-1 respectively.

The endo form was calculated to have energy of -0.05150 Hartrees, whereas the exo form was -0.05042 Hartrees. This means that the transition state for the endo form is 0.00108 Hartrees lower in energy which is equivalent to 0.68 kcalmol^-1. Therefore the endo product is predicted to be the kinetic product.

The HOMOs of the endo (left) and exo (right) Transition States are shown below.

The HOMO of the endo TS demonstrates that there is no secondary orbital overlap between the pi systems of the C=C and maleic conjugated carbonyl systems as one might expect due to their proximity. The reason for this may be due to the differing energies of the two systems (with the oxygens being highly electronegative and thus lowering the energy of the maleic fragment) therefore making it impossible for the orbitals to interact.

In the exo TS there is a close proximity of the maleic (C=O)-O-(C=O) and the bridging CH2-CH2 group as shown below. This steric clash, which does not exist for the endo conformation, is predicted to raise the energy of the exo TS and therefore make it the more unfavourable energetic pathway.

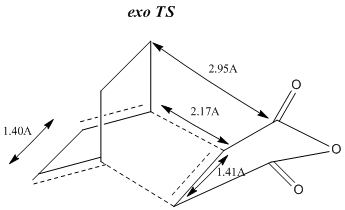sp² C-C bond length ≈ 1.35A

sp³ C-C bond length ≈ 1.55A

Van der Waals Carbon radius ≈ 1.70A

Therefore, it can be seen that our TS half-bond (2.17A) fits no existing category. Its can be described as having approximately intermediate character between an sp³ C-C (1.55A) and a V.d.W C-C bond length (3.40A).

Determination of Activation Energies

The reactants and exo and endo transition states were optimised using a high level of theory, B3LYP/6-31G*. The results are displayed below, and relate to the energies at 0k.

*Energies of reactants and transition states at 0K*
Species	Energy/Hartrees
maleic anhydride	-377.18538
cyclohexadiene	-232.14244
endo TS	-609.32100
exo TS	-609.31652

ΔE endo = 0.00682 Hartrees = 4.28 kcalmol^-1

ΔE exo = 0.0113 Hartrees = 7.09 kcalmol^-1

With this higher level of theory the endo TS is again confirmed as being the most energetically favourable transition state. Also note that these activation energies are significantly lower than those for the basic Diels Alder. Therefore the reaction will proceed much faster under the same conditions. The reason for this has already been demonstrated as being the more favourable HOMO-LUMO orbital interaction in the transition state, due to the now lower energy dieneophile.

1. Transition State